Что такое вычислительная сложность алгоритма
Оценка сложности алгоритмов, или Что такое О(log n)
Авторизуйтесь
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
20–22 декабря, Онлайн, Беcплатно
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
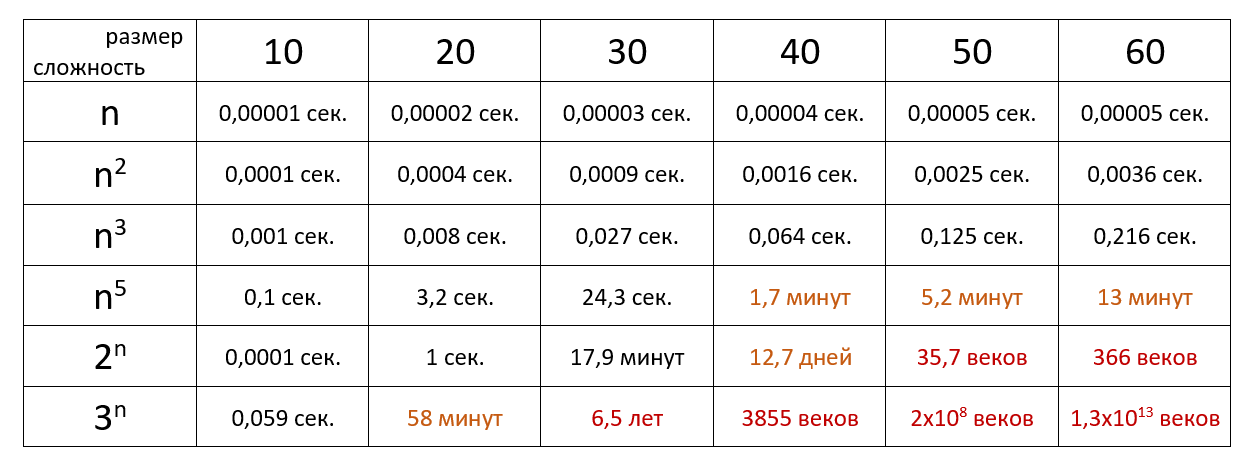
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».
Вычислительная сложность
Из Википедии — свободной энциклопедии
Вычисли́тельная сло́жность — понятие в информатике и теории алгоритмов, обозначающее функцию зависимости объёма работы, которая выполняется некоторым алгоритмом, от размера входных данных. Раздел, изучающий вычислительную сложность, называется теорией сложности вычислений. Объём работы обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством элементарных шагов, необходимых для решения задачи, тогда как пространство определяется объёмом памяти или места на носителе данных. Таким образом, в этой области предпринимается попытка ответить на центральный вопрос разработки алгоритмов: «как изменится время исполнения и объём занятой памяти в зависимости от размера входа?». Здесь под размером входа понимается длина описания данных задачи в битах (например, в задаче коммивояжёра длина входа почти пропорциональна количеству городов и дорог между ними), а под размером выхода — длина описания решения задачи (наилучшего маршрута в задаче коммивояжёра).
С теоретической информатикой тесно связаны такие области как анализ алгоритмов и теория вычислимости. Связующим звеном между теоретической информатикой и алгоритмическим анализом является тот факт, что их формирование посвящено анализу необходимого количества ресурсов определённых алгоритмов решения задач, тогда как более общим вопросом является возможность использования алгоритмов для подобных задач. Конкретизируясь, попытаемся классифицировать проблемы, которые могут или не могут быть решены при помощи ограниченных ресурсов. Сильное ограничение доступных ресурсов отличает теорию вычислительной сложности от вычислительной теории, последняя отвечает на вопрос какие задачи, в принципе, могут быть решены алгоритмически.
Оценка сложности алгоритмов
Введение
Для любого программиста важно знать основы теории алгоритмов, так как именно эта наука изучает общие характеристики алгоритмов и формальные модели их представления. Ещё с уроков информатики нас учат составлять блок-схемы, что, в последствии, помогает при написании более сложных задач, чем в школе. Также не секрет, что практически всегда существует несколько способов решения той или иной задачи: одни предполагают затратить много времени, другие ресурсов, а третьи помогают лишь приближённо найти решение.
Всегда следует искать оптимум в соответствии с поставленной задачей, в частности, при разработке алгоритмов решения класса задач.
Важно также оценивать, как будет вести себя алгоритм при начальных значениях разного объёма и количества, какие ресурсы ему потребуются и сколько времени уйдёт на вывод конечного результата.
Этим занимается раздел теории алгоритмов – теория асимптотического анализа алгоритмов.
Предлагаю в этой статье описать основные критерии оценки и привести пример оценки простейшего алгоритма. На Хабрахабре уже есть статья про методы оценки алгоритмов, но она ориентирована, в основном, на учащихся лицеев. Данную публикацию можно считать углублением той статьи.
Определения
Основным показателем сложности алгоритма является время, необходимое для решения задачи и объём требуемой памяти.
Также при анализе сложности для класса задач определяется некоторое число, характеризующее некоторый объём данных – размер входа.
Итак, можем сделать вывод, что сложность алгоритма – функция размера входа.
Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.
Существуют понятия сложности в худшем, среднем или лучшем случае. Обычно, оценивают сложность в худшем случае.
Временная сложность в худшем случае – функция размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.
Ёмкостная сложность в худшем случае – функция размера входа, равная максимальному количеству ячеек памяти, к которым было обращение при решении задач данного размера.
Порядок роста сложности алгоритмов
Порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. Из этого следует, что при оценке временной сложности нет необходимости рассматривать элементарные операции, достаточно рассматривать шаги алгоритма.
Шаг алгоритма – совокупность последовательно-расположенных элементарных операций, время выполнения которых не зависит от размера входа, то есть ограничена сверху некоторой константой.
Виды асимптотических оценок
O – оценка для худшего случая
Рассмотрим сложность f(n) > 0, функцию того же порядка g(n) > 0, размер входа n > 0.
Если f(n) = O(g(n)) и существуют константы c > 0, n0 > 0, то
0 n0.
Функция g(n) в данном случае асимптотически-точная оценка f(n). Если f(n) – функция сложности алгоритма, то порядок сложности определяется как f(n) – O(g(n)).
Данное выражение определяет класс функций, которые растут не быстрее, чем g(n) с точностью до константного множителя.
Примеры асимптотических функций
| f(n) | g(n) |
|---|---|
| 2n 2 + 7n — 3 | n 2 |
| 98n*ln(n) | n*ln(n) |
| 5n + 2 | n |
| 8 | 1 |
Ω – оценка для лучшего случая
Критерии оценки сложности алгоритмов
Равномерный весовой критерий (РВК) предполагает, что каждый шаг алгоритма выполняется за одну единицу времени, а ячейка памяти за одну единицу объёма (с точностью до константы).
Логарифмический весовой критерий (ЛВК) учитывает размер операнда, который обрабатывается той или иной операцией и значения, хранимого в ячейке памяти.
Временная сложность при ЛВК определяется значением l(Op), где Op – величина операнда.
Ёмкостная сложность при ЛВК определяется значением l(M), где M – величина ячейки памяти.
Пример оценки сложности при вычислении факториала
Необходимо проанализировать сложность алгоритма вычисление факториала. Для этого напишем на псевдокоде языка С данную задачу:
Временная сложность при равномерном весовом критерии
Достаточно просто определить, что размер входа данной задачи – n.
Количество шагов – (n — 1).
Таким образом, временная сложность при РВК равна O(n).
Временная сложность при логарифмическом весовом критерии
В данном пункте следует выделить операции, которые необходимо оценить. Во-первых, это операции сравнения. Во-вторых, операции изменения переменных (сложение, умножение). Операции присваивания не учитываются, так как предполагается, что она происходят мгновенно.
Итак, в данной задаче выделяется три операции:
Сложность алгоритмов. Big O. Основы.
Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.
Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.
Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.
Распространённые сложности алгоритмов
Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.
Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.
Пример № 1.
У нас есть массив из 5 чисел и нам надо получить первый элемент.
Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.
Пример № 2.
Сложение двух чисел. Функция всегда выполняет константное количество операций.
Пример № 3.
Размер массива. Опять же, функция всегда выполняет константной количество операций.
Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.
Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.
Пример № 3.
Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.
К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.
Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.
Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.
Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.
Такие алгоритмы легко узнать по вложенным циклам.
Пример № 1.
В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n 2 )
Зачем изучать Big O
Шпаргалка
Небольшие подсказки, которые помогут определить сложность алгоритма.
Полезные ссылки
Что такое вычислительная сложность алгоритма
ЛЕКЦИЯ № 1 (некоторые сведения из курса «Алгоритмы и структуры данных»)
1. ПОНЯТИЕ АЛГОРИТМА
2. ЭФФЕКТИВНОСТЬ АЛГОРИТМА
3. КЛАССЫ СЛОЖНОСТИ
Алгоритм относится к основным понятиям математики, а поэтому не имеет определения. В теории алгоритмов были введены различные формальные определения алгоритма и удивительным научным результатом является доказательство эквивалентности этих формальных определений в смысле их равномощности.
Варианты словесного определения алгоритма принадлежат российским ученым А. Н. Колмогорову и А.А. Маркову :
Определение (Колмогоров): Алгоритм – это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
Определение (Марков): Алгоритм – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.
Отметим, что различные определения алгоритма, в явной или неявной форме, постулируют следующий ряд требований:
— алгоритм должен содержать конечное количество элементарно выполнимых предписаний, т.е. удовлетворять требованию конечности записи;
— алгоритм должен выполнять конечное количество шагов при решении задачи, т.е. удовлетворять требованию конечности действий;
— алгоритм должен быть единым для всех допустимых исходных данных, т.е. удовлетворять требованию универсальности;
— алгоритм должен приводить к правильному по отношению к поставленной задаче решению, т.е. удовлетворять требованию правильности.
Другие формальные определения понятия алгоритма связаны с введением специальных математических конструкций (машина Поста, машина Тьюринга, рекурсивно-вычислимые функции Черча) и постулированием тезиса об эквивалентности такого формализма и понятия «алгоритм».
С алгоритмами связаны приведенные ниже области исследований.
— Анализ алгоритмов. Предмет этой области состоит в том, чтобы для заданного алгоритма определить рабочие характеристики. Например, желательно, чтобы алгоритм был быстрым.
— Теория алгоритмов. В этой области рассматриваются вопросы существования или не существования эффективных алгоритмов вычисления определенных величин.
— Построение алгоритмов. В этой области рассматриваются стандартные приемы и методы, используемые при написании алгоритмов.
При работе с некоторыми алгоритмами могут стать проблемой ограничения памяти. Процесс может потребовать большого временного хранения, ограничивающего размер первоначального набора данных, или вызвать требующую времени дисковую подкачку. Эффективность пространства ( space effi ciency ) — это мера относительного количества внутренней памяти, исполь зуемой каким-либо алгоритмом. Она может указать, какого типа компьютер способен выполнять этот алгоритм и полную системную эффективность ал горитма. Вследствие увеличения объема памяти в новых системах, анализ пространственной эффективности становится менее важным.
Интуитивно вычислительная эффективность алгоритма из меряется количеством обрабатываемых им данных для определения ключе вых операций алгоритма. Эти операции могут зависеть от типа данных, количества данных и их начального упорядочения.
Определяя вычислительную эффективность алгоритма, мы ассоциируем функцию f ( n ) с количеством сравнений. В действительности, точная форма функции может быть трудна для определения, и поэтому мы используем методы аппроксимации для определения хорошей верхней границы функции.
Определение: Функция f(n) имеет порядок O ( g ( n )), если имеется константа К и счетчик n0,такие, что f ( n ) K * g ( n ), для n > n0.
Интуитивно это означает, что функция g в конечном счете превышает значение функции f. Мы говорим, что вычислительная сложность ( computational complexity ) (или порядок) алгоритма равна O ( g ( n )).
Вычисление времени выполнения программ
В общем случае время выполнения конечной последовательности программных фрагментов, без учета констант, имеет порядок фрагмента с наибольшим временем выполнения. Иногда возможна ситуация, когда порядки роста времен нескольких фрагментов несоизмеримы (ни один из них не больше, чем другой, но они и не равны). Для примера рассмотрим два фрагмента с временем выполнения O ( f ( n )) и O ( g ( n )), где
Правило произведений заключается в следующем. Если T 1 ( n ) и T 2 ( n ) имеют степени роста O ( f ( n )) и O ( g ( n )) соответственно, то произведение
T 1 ( n ) x T 2 ( n ) имеет степень роста O ( f ( n ) x g ( n )). Из правила произведений следует, что O ( cf ( n )) эквивалентно O ( f ( n )), если с – положительная константа. Например, O(n 2 / 2) эквивалентно O(n 2 ).
Прежде чем переходить к общим правилам анализа времени выполнения программ, рассмотрим простой пример, иллюстрирующий процесс определения времени выполнения.
Рассмотрим программу сортировки bubble (пузырек), которая упорядочивает массив целых чисел в возрастающем порядке методом «пузырька». За каждый проход внутреннего цикла (операторы (3)–(6)) «пузырек» с наименьшим элементом «всплывает» в начало массива.
Число элементов n, подлежащих сортировке, может служить мерой объема входных данных. Сначала отметим, что все операторы присваивания имеют некоторое постоянное время выполнения, независящее от размера входных данных. Таким образом, операторы (4) – (6) имеют время выполнения порядка O(1). Запись O(1) означает «равнозначно некой константе».
В соответствии с правилом сумм время выполнения этой группы операторов равно O(mах(1, 1, 1)) = O(1).
Теперь необходимо подсчитать время выполнения условных и циклических операторов. Операторы if и for вложены друг в друга, поэтому мы пойдем от внутренних операторов к внешним, последовательно определяя время выполнения условного оператора и каждой итерации цикла. Для оператора if проверка логического выражения занимает время порядка O(1).
Мы не знаем, будут ли выполняться операторы в теле условного оператора (строки (4) – (6)), но поскольку мы ищем наихудшее время выполнения, то, естественно, предполагаем, что они выполняются. Таким образом, получаем, что время выполнения группы операторов (3) – (6) имеет порядок O(1).
Далее рассмотрим группу (2) – (6) операторов внутреннего цикла.
Общее правило вычисления времени выполнения цикла заключается в суммировании времени выполнения каждой итерации цикла. Для операторов
(2) – (6) время выполнения на каждой итерации имеет порядок O(1). Цикл выполняется п – i раз, поэтому по правилу произведений общее время выполнения цикла имеет порядок O((n – i) х 1), что равно O(n – i).
Теперь перейдем к внешнему циклу, который содержит все исполняемые операторы программы. Оператор (1) выполняется n – 1 раз, поэтому суммарное время выполнения программы ограничено сверху выражением
которое имеет порядок O(n 2 ). Таким образом, программа «пузырька» выполняется за время, пропорциональное квадрату числа элементов, подлежащих упорядочиванию. В главе 3 будут рассмотрены программы с временем выполнения порядка O(п log n ), которое существенно меньше O(n 2 ), поскольку при больших n log n [1] значительно меньше n.
Перед формулировкой общих правил анализа программ позвольте напомнить, что нахождение точной верхней границы времени выполнения программ только в редких случаях так же просто, как в приведенном выше примере, в общем случае эта задача является интеллектуальным вызовом исследователю. Поэтому не существует исчерпывающего множества правил анализа программ. Можно дать только некоторые советы и проиллюстрировать их с разных точек зрения примерами, приведенными в этом пособии.
Дадим несколько правил анализа программ. В общем случае время выполнения оператора или группы операторов можно параметризовать с помощью размера входных данных и/или одной или нескольких переменных.
Но для времени выполнения программы в целом допустимым параметром может быть только п, размер входных данных.
1. Время выполнения операторов присваивания, чтения и записи обычно имеет порядок O(1). Есть несколько исключений из этого правила, например в языке PL / 1, где можно присваивать большие массивы, или в любых других языках, допускающих вызовы функций в операторах присваивания.
2. Время выполнения последовательности операторов определяется с помощью правила сумм. Поэтому степень роста времени выполнения последовательности операторов без определения констант пропорциональности совпадает с наибольшим временем выполнения оператора в данной последовательности.
3. Время выполнения условных операторов состоит из времени выполнения условно исполняемых операторов и времени вычисления самого логического выражения. Время вычисления логического выражения обычно имеет порядок O (1). Время для всей конструкции if — then — else состоит из времени вычисления логического выражения и наибольшего из времени, необходимого для выполнения операторов, исполняемых при значении логического выражения true (истина) и при значении false (ложь).
4. Время выполнения цикла является суммой времени всех исполняемых итераций цикла, в свою очередь состоящих из времени выполнения операторов тела цикла и времени вычисления условия прекращения цикла (обычно последнее имеет порядок O(1)). Часто время выполнения цикла вычисляется, пренебрегая определением констант пропорциональности, как произведение количества выполненных итераций цикла на наибольшее возможное время выполнения операторов тела цикла. Время выполнения каждого цикла, если в программе их несколько, должно определяться отдельно.
Естественной мерой объема входных данных для функции fact является значение n. Обозначим через Т(n) время выполнения программы. Время выполнения для строк (1) и (2) имеет порядок O (1), а для строки (3) – O(1) + Т(n – 1). Таким образом, для некоторых констант с и d имеем
Из (1.2) следует, что Т(n) имеет порядок O(n). Отметим, что в этом примере анализа программы мы предполагали, что операция перемножения двух целых чисел имеет порядок O(1). На практике, однако, программу, представленную выше, нельзя использовать для вычисления факториала при больших значений n, так как размер получаемых в процессе вычисления целых чисел может превышать длину машинного слова.
Общий метод решения рекуррентных соотношений, подобных соотношению из рассмотренного примера, состоит в последовательном раскрытии выражений T ( k ) в правой части уравнения (путем подстановки в исходное соотношение k вместо п) до тех пор, пока не получится формула, у которой в правой части отсутствует Т (как в формуле (1.2)). При этом часто приходится находить суммы различных последовательностей. Если значения таких сумм нельзя вычислить точно, то для сумм находятся верхние границы, что позволяет, в свою очередь, получить верхние границы для Т(n).
Программы с операторами безусловного перехода
При анализе времени выполнения программ мы неявно предполагали, что все ветвления в ходе выполнения процедур осуществлялись с помощью условных операторов и операторов циклов. Мы останавливаемся на этом факте, так как определяли время выполнения больших групп операторов путем применения правила сумм к этим группам. Однако операторы безусловного перехода (такие как goto ) могут порождать более сложную логическую групповую структуру. В принципе, операторы безусловного перехода можно исключить из программы.
Предлагается следующий подход для работы с операторами безусловного перехода, выполняющих выход из циклов, который гарантирует отслеживание всего цикла. Поскольку досрочный выход из цикла, скорее всего, осуществляется после выполнения какого-нибудь логического условия, то можно предположить, что это условие никогда не выполняется. Но этот консервативный подход никогда не позволит уменьшить время выполнения программы, так как мы предполагаем полное выполнение цикла. Для программ, где досрочный выход из цикла не исключение, а правило, консервативный подход значительно переоценивает степень роста времени выполнения в наихудшем случае. Если же переход осуществляется к ранее выполненным операторам, то в этом случае вообще нельзя игнорировать оператор безусловного перехода, поскольку такой оператор создает петлю в выполнении программы, что приводит к нарастанию времени выполнения всей программы.
Полиномиальные и экспоненциальные алгоритмы.
Обобщение линейности дает нам первый большой класс алгоритмов – полиномиальных.
Полиномиальным (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность есть O(p(n)), где p(n) – полином от n. Задачи, для решения которых известен алгоритм, сложность которого составляет полином заданной, постоянной и не зависящей от размерности входной величины n степени, называют “хорошими” и относят их к классу P.
Соответственно и алгоритмы, в оценку сложности которых n входит в показатель степени, относятся к экспоненциальным.
Необходимо отметить, что при небольших значениях n экспоненциальный алгоритм может быть даже менее сложным, чем полиномиальный. Тем не менее различие между этими типами алгоритмов весьма велико, проявляясь при больших значениях n.
Особую группу по значениям сложности, близким к полиномиальным, составляют алгоритмы, сложность которых является полиномиальной функцией от log(n) (поскольку log(n) растёт медленнее, чем n).
Определение (Гэри,Джонсон)
(1) Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность равна O(p(n)), где р(n) — некоторая функция полиномиального роста, a n — входная длина.
(2) Алгоритмы, временная сложность которых не поддается подобной оценке, будем называть экспоненциальными алгоритмами.
Следует отметить, что это определение включает и такие функции, как nlog(n), — хотя они и не являются полиномиальными, но обычно не считаются экспоненциальными.
Сложностью алгоритма называется количество действий в вычислительном процессе этого алгоритма.
Сложность алгоритма оценивают по его динамическим характеристикам, а не по статическим: например, большая программа может выполняться очень быстро, а короткая – очень долго. На практике сложность алгоритма обычно связывают с основным его параметром, существенно влияющим на количество выполняемых действий. Как правило, это размер массива обрабатываемых данных (размер задачи).
Наихудший случай может быть важен, так как эти обстоятельства будут наиболее негативно влиять на ваше приложение. Клиент может не допускать наихудшего случая и может предпочесть, чтобы вы выбрали алгоритм, который имеет более узкий диапазон эффективности. В общем, довольно трудно математически определить среднюю эффективность какого-либо алгоритма. Мы будем использовать только очень простые измере ния ожидаемых значений и оставим математические детали для курса по тео рии сложности.
Общий порядок величин
Небольшой набор различных порядков определяет сложность большинства алгоритмов структур данных. Мы определяем различные порядки и описываем ал горитмы, приводящие в результате к таким оценкам.
Если алгоритм — порядка 0(1), то этот порядок не зависит от количества элементов данных в коллекции. Этот алгоритм выполняется за постоянную единицу времени ( constant time ). Например, присваивание некоторого зна чения элементу списка массива имеет порядок 0(1), при условии, что вы храните индекс, который определяет конец списка. Сохранение этого эле мента включает только простой оператор присваивания.
Алгоритм О(n) является линейным ( linear ). Сложность этого алгоритма пропорциональна размеру списка. Например, вставка элемента в конец списка п элементов будет линейной, если мы не храним ссылку на конец списка. Подразумевая, что мы можем просматривать элемент за элементом, алгоритм требует, чтобы мы протестировали n элементов перед определением конца списка. Порядком этого процесса является О(n). Нахождение максимального элемента в массиве из п элементов — это О(п), потому что должен быть проверен каждый из n элементов.
Ряд алгоритмов имеют порядок, включающий log 2 n , и называются лога рифмическими ( logarithmic ). Эта сложность возникает, когда алгоритм не однократно подразделяет данные на подсписки, длиной 1/2, 1/4, 1/8, и так далее от оригинального размера списка. Логарифмические порядки возника ют при работе с бинарными деревьями. Бинарный поиск имеет сложность среднего и наихудшего случаев O ( log 2 n ).
Алгоритмы, имеющие порядок О(n 2 ), являются квадратическими ( quad ratic ). Наиболее простые алгоритмы сортировки такие, как обменная сорти ровка, имеют порядок О(n 2 ). Квадратические алгоритмы используются на практике только для относительно небольших значений га. Всякий раз, когда n удваивается, время выполнения такого алгоритма увеличивается на мно житель 4. Алгоритм показывает кубическое ( cubic ) время, если его порядок равен О( n 3 ), и такие алгоритмы очень медленные. Всякий раз, когда n уд ваивается, время выполнения алгоритма увеличивается в восемь раз. Алго ритм Уоршела, применимый к графам, — это алгоритм порядка О(n 3 ).
Алгоритм со сложностью О(2 n ) имеет экспоненциальную сложность ( ex ponential complexity ). Такие алгоритмы выполняются настолько медленно, что они используются только при малых значениях n. Этот тип сложности часто ассоциируется с проблемами, требующими неоднократного поиска де рева решений.
В таблице приводятся линейный, квадратичный, кубический, экспо ненциальный и логарифмический порядки величины для выбранных значе ний n.