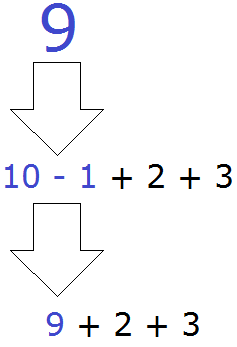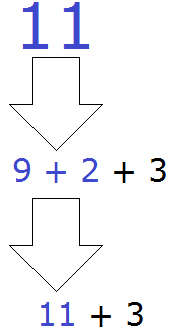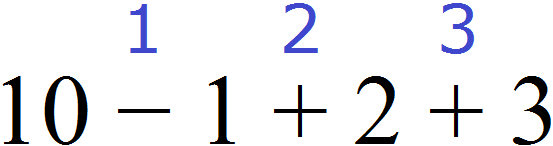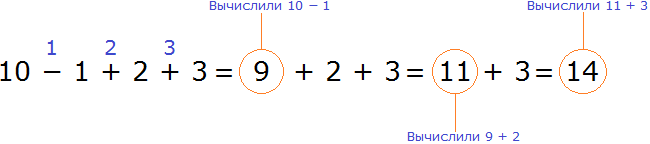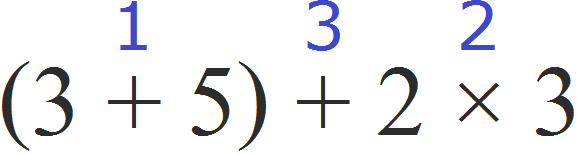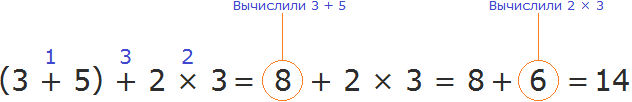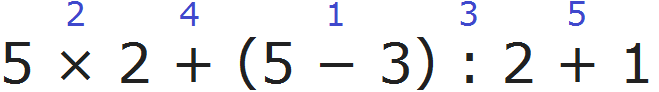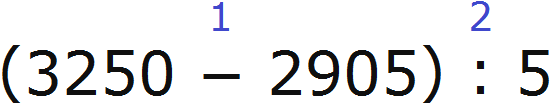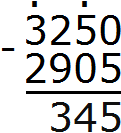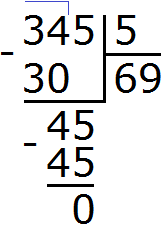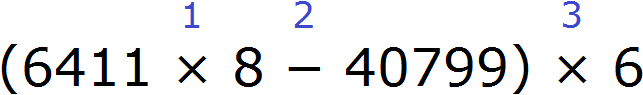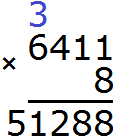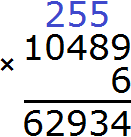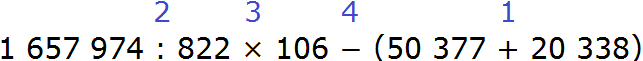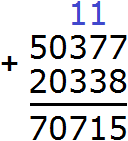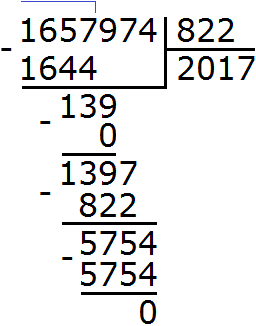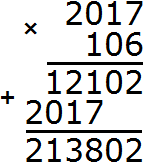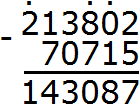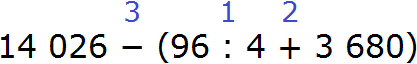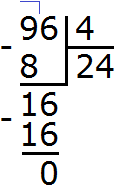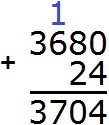Что такое выполни действия
Порядок действий
В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.
Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.
Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:
10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1
Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.
Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:
Сначала вычислить то, что находится в скобках!
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:
Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!
Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:
1. Сначала вычислить то, что находится в скобках!
2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!
3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!
Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14
10 − 1 + 2 + 3 = 14
Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:
И далее можно выполнить действия по отдельности, что очень удобно:
1) 10 − 1 = 9
2) 9 + 2 = 11
3) 11 + 3 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:
Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.
Пример 2. Найти значение выражения (3 + 5) + 2 × 3
Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
Сначала вычислить то, что находится в скобках!
8 + 2 × 3
Снова читаем первое правило:
Сначала вычислить то, что находится в скобках!
Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
8 + 6
Осталось простейшее выражение 8 + 6, которое вычисляется легко:
Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14
(3 + 5) + 2 × 3 = 14
Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:
И далее можно выполнить действия по отдельности, что очень удобно:
1) 3 + 5 = 8
2) 2 × 3 = 6
3) 8 + 6 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
Но опять же, используя такой способ, нужно быть очень внимательным.
Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1
Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:
1) 5 − 3 = 2
2) 5 × 2 = 10
3) 2 : 2 = 1
4) 10 + 1 = 11
5) 11 + 1 = 12
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
Пример 4. Найти значение выражения (3250 − 2905) : 5
Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым
1) 3250 − 2905 = 345
2) 345 : 5 = 69
В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.
Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.
В результате будем иметь следующий порядок:
1) 6 411 × 8 = 51 288
2) 51 288 − 40 799 = 10 489
3) 10 489 × 6 = 62 934
Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)
Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.
1) 50 377 + 20 338 = 70 715
2) 1 657 974 : 822 = 2 017
3) 2 017 × 106 = 213 802
4) 213 802−70 715 = 143 087
Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.
В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:
1) 96 : 4 = 24
2) 24 + 3 680 = 3 704
3) 14026 − 3 704 = 10 322
Порядок действий в математике
В данной публикации мы рассмотрим правила в математике касательно порядка выполнения арифметических действий (в том числе в выражениях со скобками, возведением в степень или извлечением корня), сопроводив их примерами для лучшего понимания материала.
Порядок выполнения действий
Отметим сразу, что действия рассматриваются от начала примера к его концу, т.е. слева направо.
Общее правило
сначала выполняются умножение и деление, а затем сложение и вычитание полученных промежуточных значений.
Над каждым действием мы написали число, которое соответствует порядку его выполнения, т.е. решение примера состоит из трех промежуточных действий:
Немного потренировавшись в дальнейшем можно все действия выполнять цепочкой (в одну/несколько строк), продолжая исходное выражение. В нашем случае получается:
2 ⋅ 4 + 12 : 3 = 8 + 4 = 12.
Если подряд идут несколько действий умножения и деления, то они также выполняются подряд, и их можно объединить при желании.
Примеры со скобками
Действия в скобках (если они есть) выполняются в первую очередь. А внутри них действует все тот же принятый порядок, описанный выше.
Решение можно разбить на действия ниже:
При расстановке действий выражение в скобках можно условно воспринимать как одно целое/число. Для удобства мы выделили его в цепочке ниже зеленым цветом:
Скобки в скобках
Иногда в скобках могут быть еще одни скобки (называются вложенными). В таких случаях сперва выполняются действия во внутренних скобках.
Раскладка примера в цепочку выглядит так:
Возведение в степень/извлечение корня
Данные действия выполняется в самую первую очередь, т.е. даже до умножения и деления. При этом если они касаются выражения в скобках, то сначала производятся вычисления внутри них. Рассмотрим пример:
Действия первой и второй ступени
Арифметические действия делятся на действия первой и второй ступени.
Порядок действий
Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.
Пример 1. Вычислить значение выражения:
Решение: Данное выражение содержит действия только одной ступени — первой (сложение и вычитание). Надо определить порядок действий и выполнить их.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| 15 | + | 17 | — | 20 | + | 8 | — | 12 |
Пример 2. Вычислить значение выражения:
Решение: Данное выражение содержит действия только одной ступени — второй (умножение и деление). Надо определить порядок действий и выполнить их.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| 60 | : | 15 | · | 7 | : | 2 | · | 3 |
Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.
Пример. Вычислить значение выражения:
Решение: Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым — умножение, третьим — сложение, а четвёртым — вычитание.
Правила выполнения математических действий
Основные операции в математике
Основными действиями являются:
Наряду с этими операциями предусмотрены отношения:
Сложение является операцией для объединения пары слагаемых.
Сложение записывают таким образом:
5, 1 — слагаемые, 6 — сумма.
Вычитание — операция, которая является обратным действием сложению.
Записывать вычитание следует таким образом:
10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
При сложении разности в виде 9 и вычитаемого в виде 1 можно получить 10, которое является уменьшаемым. Сложение можно проверить вычитанием:
Умножение является действием в арифметике и имеет вид сокращенной записи сложения идентичных слагаемых.
В данном случае 3 — множимое, 4 — множитель, 12 — произведение.
Множимое и множитель можно поменять местами. При этом произведение не поменяется:
В связи с этим, множитель и множимое являются сомножителями.
Деление — арифметическая операция, которая является обратным действием умножению.
Деление, в том числе для многочленов, записывают таким образом:
При умножении делителя на частное получаем делимое, то есть:
В некоторых уравнениях можно встретить на месте частного не целое число. В таком случае его допустимо записать в виде дроби.
Возведение в степень является действием умножения числа на самого себя несколько раз.
Основанием степени является число, повторяющееся сомножителем конкретное количество раз. Роль показателя степени играет число, указывающее на то количество раз, которое берется одинаковый множитель. Степень — число, являющееся результатом взаимодействия основания и показателя степени.
Здесь 3 является основанием степени, 4 определяется, как показатель степени, 81 называют степенью.
Вторая степень — квадрат, а третья степень — куб. Первая степень числа является самим числом.
В данном случае 81 является подкоренным числом, 4 — показатель корня, 3 — корень.
С целью проверки операции по извлечению корня можно возвести 3 в степень 4, что в результате дает 81:
Квадратный корень — это корень второй степени:
Если предполагается запись квадратного корня, то показатель корня допускается не записывать:
Кубический корень — это корень третьей степени:
Сложение является обратным действием вычитанию, умножение — делению, возведение в степень — извлечению корня, и наоборот.
Порядок вычисления простых выражений
Перед решением простых уравнений полезно ознакомиться с последовательностью действий:
Рассмотреть это правило можно на практике.
Нужно решить письменное уравнение:
В первую очередь следует проверить, есть ли скобки для группировки элементов выражения. Здесь они отсутствуют, как и операции умножения и деления. Тогда можно выполнять действия, руководствуясь стандартным алгоритмом, описанным выше: витаем 2 из 11, складываем остаток с 5, в результате получим 14.
11 – 2 + 5 = 9 + 5 = 14
Скобки в данном примере отсутствуют, но имеются операции деления и умножения. При их обнаружении нужно с помощью правила последовательно выполнять действия, двигаясь слева направо: 10 делим на 2, полученное число умножаем на 7, результат делим на 5.
10 ÷ 2 × 7 ÷ 5 = 5 × 7 ÷ 5 = 35 ÷ 5 = 7
В процессе изучения данной темы, пока опыта еще не достаточно, полезно расставлять над знаками арифметических операций цифры в порядке их выполнения. Такая работа значительно упрощает вычисления и исключает ошибки.
Что такое действия первой и второй ступени
В учебной литературе по математике можно встретить такие понятия, как действие первой и второй ступени:
В том случае, когда в выражении отсутствуют скобки, операции выполняются в следующем порядке:
Порядок вычислений в выражениях со скобками
Наличие в выражении скобок изменяет стандартный алгоритм арифметических операций. Это своеобразный индикатор для действий, которые должны быть выполнены в первую очередь.
В первую очередь следует выполнить операции, заключенные в скобках. При этом важно соблюдать стандартный порядок действий, то есть слева направо умножать и делить, а далее — складывать и вычитать.
Выражения, заключенные в скобках, являются составными компонентами начального выражения. Для таких выражений стандартный алгоритм действий остается без изменений. Рассмотреть вычисления можно на практических примерах.
Так как в выражении есть скобки, в первую очередь нужно выполнить действия в этих скобках:
Руководствуясь стандартным алгоритмом, сначала умножаем, затем — вычитаем:
Перейдем ко второму выражению, заключенному в скобках:
Так как в данном случае имеется лишь вычитание, выполняем действие:
Результаты, которые получили при решении выражений в скобках, следует подставить в начальное выражение:
Сначала нужно умножить, затем поделить, а далее выполнить сложение:
10 + 2 × 8 ÷ 2 = 10 + 16 ÷ 2 = 10 + 8 = 18
Порядок действий в выражениях без скобок
В данном случае присутствуют действия сложения и вычитания, которые следует выполнять по порядку, двигаясь слева направо.
Здесь умножение и деление. Данные арифметические операции также выполняем по порядку, начиная с левой стороны, двигаясь в правую сторону.
Когда выражения содержат операции сложение и вычитание, либо деление и умножение, то вычисления нужно выполнять по порядку слева направо.
Нередко встречаются примеры, где есть сложение и вычитание, а также умножение и деление. Тогда в первую очередь делят и умножают по порядку, а на втором этапе складывают и вычитают также в определенном порядке.
Решение примеров
Согласно стандартному алгоритму, проверяем наличие скобок. Так как скобки имеются, начинаем с них:
Полученный результат следует подставить в исходное выражение:
Скобки отсутствуют, но есть умножение, которое необходимо выполнить в первую очередь:
Подставим результат в начальное выражение:
Решим полученное выражение:
Если сразу обозначить порядок действий, то запись примет вид:
Что сперва умножение или деление
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать. Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами 🙂
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!
А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя.
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
Вычислим значение выражения.
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Выполнение тренировочных заданий на изученное правило
Рассмотрим выражения, установим порядок действий и выполним вычисления.
Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Узнаем, правильно ли определен порядок действий в следующих выражениях.
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 – 9 = 1
Сначала выполняем действия в скобках:
16 – 2 · 7 + 4 = 16 – 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Выполняем действия в круглых скобках, имеем:
8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4
действия в квадратных скобках дают:
14 – 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Порядок действий:
30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150