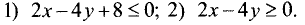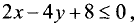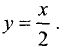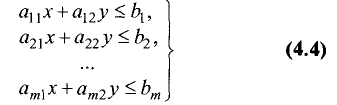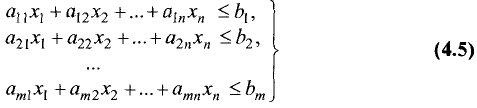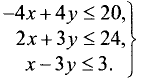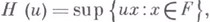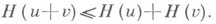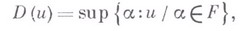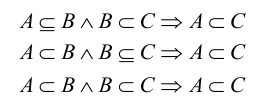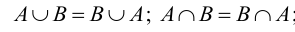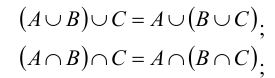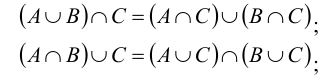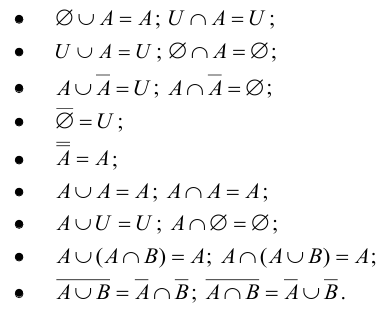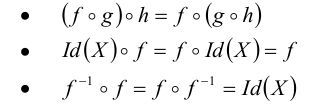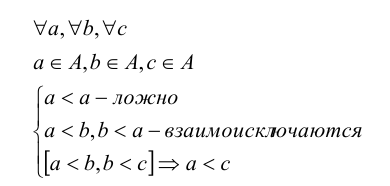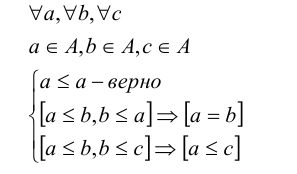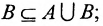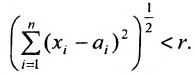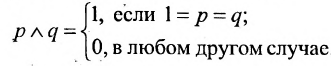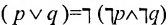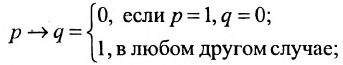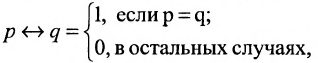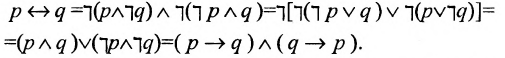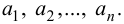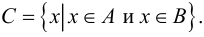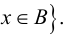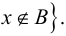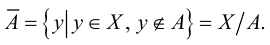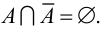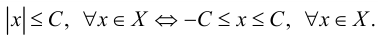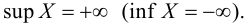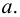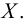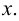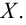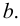Что такое выпуклое множество
Выпуклые множества точек и их свойства с примерами решения и образцами выполнения
Основные определения:
Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки.
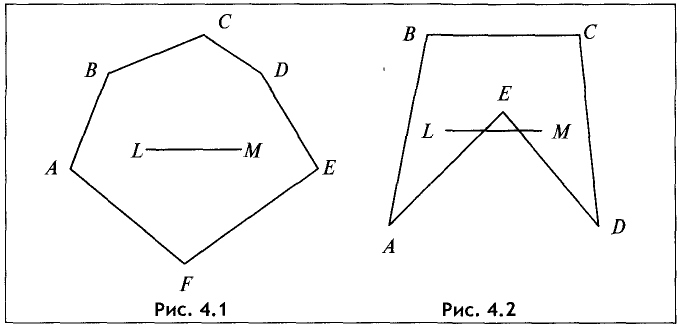
Например, многоугольник, представленный на рис. 4.1,
является выпуклым, а многоугольник на рис.4.2 выпуклым не является.
Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются прямая, круг, куб,
многогранная область, полуплоскость, полупространство и т.д.
Пересечение любого числа выпуклых множеств есть выпуклое
множество.
Точка множества называется внутренней, если в любой ее окрестности (например, круг или шар с центром в этой точке) содержатся точки только данного множества.
Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.
Точка множества называется угловой (крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.
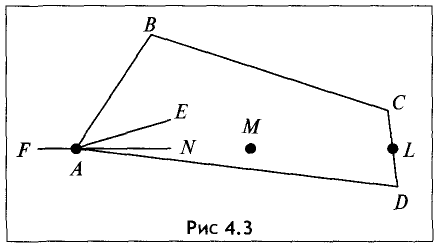
Примеры угловой А, внутренней L и граничной М точек приведены на рис. 4.3.
Точка А является угловой, так как для любого отрезка АЕ,
целиком принадлежащего многоугольнику, она не является
внутренней. Точка А — внутренняя для отрезка FN, но этот отрезок не принадлежит целиком множеству.
Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника).
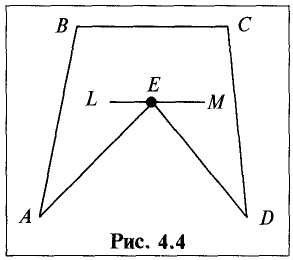
Так, на рис. 4.4 точка Е является вершиной невыпуклого многоугольника, но не является угловой, так как она является внутренней для отрезка LM, целиком принадлежащего этому
многоугольнику.
Множество точек называется замкнутым, если оно включает все свои граничные точки.
Множество точек называется ограниченным, если существует круг (шар) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.
Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек, называется выпуклым многоугольником (многогранником), если оно ограниченное, и выпуклой многоугольной (многогранной) областью, если оно неограниченное.
Введенные понятия рассматривались для множества точек на
плоскости и в пространстве. Их можно обобщить также на n-мерное
точечное пространство.
Геометрический смысл решений неравенств
Рассмотрим решения неравенств с двумя переменными типа
Теорема:
Множество решений неравенств с двумя переменными (4.1) является одной из двух полуплоскостей, на которые вся плоскость делится прямой
включая и эту прямую, а другая полуплоскость — множеством решений неравенства
Пример:
Построить график множества решений следующих
неравенств:
Решение:
В соответствии с теоремой множество решений
приведенных неравенств есть полуплоскость.
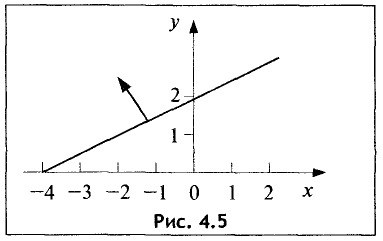
1.Границей первой полуплоскости является прямая
Представим уравнение этой прямой в виде 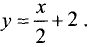
Ее график представлен на рис. 4.5.
Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Проще всего задать точку с координатами (0; 0). Подставив данные
координаты в неравенство
видим, что оно не выполняется, так как 8 > 0. Поэтому искомой является верхняя полуплоскость.
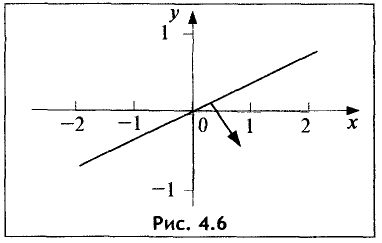
2.Границей второй полуплоскости является прямая
Представим это уравнение в виде
График исследуемой прямой представлен на рис. 4.6.
В данном случае точка с координатами (0; 0) лежит на этой
прямой. Поэтому выбираем точку с координатами (0; —1) и подставляем данные координаты в неравенство 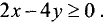
Основные свойства выпуклого множества точек
Рассмотрим множество решений совместной системы линейных
неравенств с двумя переменными.
Теорема:
Множество решений совместной системы т линейных
неравенств с двумя переменными
является выпуклым многоугольником (или выпуклой многоугольной областью).
Знаки некоторых или всех неравенств могут быть
Эту теорему для n переменных можно сформулировать
следующим образом.
Теорема:
Множество решений совместной системы m линейных
неравенств с n переменными
является выпуклым многогранником (или выпуклой многогранной областью) в n-мерном пространстве.
Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы.
Область решений системы, удовлетворяющая условиям неотрицательности 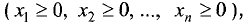
Пример:
Построить область решений и область допустимых
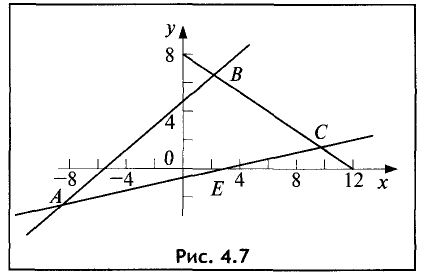
решений системы неравенств и определить координаты угловых точек области допустимых решений:
Решение:
Областью решений является треугольник ABC, представленный на рис. 4.7.
Для нахождения искомой полуплоскости зададим контрольную
точку с координатами (0; 0). Подставив данные координаты в неравенство 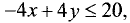
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Выпуклые оболочки
Выпуклое множество — такое множество точек, что, для любых двух точек множества, все точки на отрезке между ними тоже принадлежат этому множеству.
Выпуклая оболочка множества точек — такое выпуклое множество точек, что все точки фигуры также лежат в нем.
Минимальная выпуклая оболочка множества точек — это минимальная по площади выпуклая оболочка.
Для экономии времени дальше минимальные выпуклые оболочки мы будем называть просто выпуклыми оболочками.
Для практических целей выпуклые оболочки полезны тем, что они компактно хранят всю необходимую информацию о множестве точек, что позволяет быстро отвечать на разнообразные запросы на этом множестве.
Выпуклые оболочки можно рассматривать в любом пространстве, но в этой статье мы ограничимся двумерным и научимся их эффективно строить по какому-то множеству из \(n\) точек на плоскости.
Алгоритм Джарвиса
Корректность алгоритма легко доказывается по индукции:
На первом шаге мы выбрали точку, точно лежащую в МВО.
Алгоритм Джарвиса также называют алгоритмом заворачивания подарка: мы каждый раз находим самый близкий «угол».
В реализации будем пользоваться тем же классом для точки, что и в статье про вычислительную геометрию. Для краткости, будем считать, что все точки различны, имеют целочисленные координаты, а также что нет трёх точек на одной прямой.
Алгоритм Грэхема

Верхние и нижние огибающие
Для весьма большого количества применений нам на самом деле нужны не выпуклые оболочки, а только их половины (правые и левые или верхние и нижние), которые называют огибающими (англ. envelope).
Огибающие строить немного проще: можно отсортировать точки по \(x\) и пройтись по ним в таком порядке, поддерживая на стеке верхнюю огибающую для текущего префикса. При добавлении очередной точки нам нужно аналогичным образом проверить и удалить сколько-то верхних точек на стеке:
Алгоритм Эндрю
Для построения выпуклой оболочки можно поступить следующим образом: построить верхнюю огибающую, построить нижнюю огибающую, а затем просто объединить их списки.
Динамические выпуклые оболочки
Обрабатывать удаление точки из множества сложнее. Если запросы известны заранее, то проще воспользоваться идеями корневой эвристики или dynamic connectivity problem и поддерживать только те точки, которые существуют на всем текущем блоке, и сводить удаление к добавлению.
Если же запросы удаления требуется обрабатывать онлайн (fully dynamic convex hull), то для этого есть очень неприятный алгоритм на 250-300 строк кода, заключающийся в поддержании огибающих для всех поддеревьев в этом дереве поиска и быстром объединении огибающих при перестроении дерева. Алгоритм работает за \(O(\log^2 n)\) на запрос: при слиянии огибающих при объединении вершин используется бинпоиск с разбором кучи случаев.
Алгоритм Чана
Алгоритм. Разделим все точки на группы по \(m\) точек. В каждой группе построим выпуклую оболочку за \(O(m \log m)\) алгоритмом Грэхэма. Точки никак не упорядочены, и эти оболочки могут пересекаться — это нормально. Суммарно для всех групп понадобится \(O(n \log m)\) операций.
Понятно, что ни при каких применимых на практике ограничениях, даже если оболочка состоит из трёх точек, этот алгоритм не будет быстрее обычного алгоритма Грэхэма, так что автор не будет приводить его реализацию. Этот способ просто интересен с теоретической точки зрения.
Пересечение полуплоскостей
Очень похожей задачей является пересечение полуплоскостей (англ. half-plane intersection). Требуется найти множество, удовлетворяющее набору неравенств:
\[ a_i x + b_i y + c \geq 0 \]
Например, через сведение к пересечению полуплоскостей можно (не самым оптимальным образом) строить подобные клёвые картинки:
Результатом пересечения множества полуплоскостей тоже будет выпуклая оболочка — полуплоскость это выпуклое множество, а пересечение любых выпуклых множеств тоже выпуклое. Возможно, эта оболочка будет бесконечной по каким-то направлениям. Чтобы не обрабатывать это отдельно, часто добавляют bounding box — «коробку» из четырёх полуплоскостей на большом удалении.
Один из способов построения — построить отдельно верхнюю и нижнюю огибающую и пересечь. Для этого нужно разделить все полуплоскости на «смотрящие вверх» и «смотрящие вниз», для обеих групп отсортировать их по углу вектора нормали и пройтись по ним со стеком, удаляя «ненужные» полуплоскости — те, которые полностью покрываются новой и предпоследней полуплоскостью в стеке.
Нахождение касательной
В некоторых задачах нам на самом деле не нужно явно находить пересечение, а достаточно лишь определить, пустое оно или нет. В блоге Петра Митричева описан простой алгоритм, позволяющий это делать за линейное время.
Если это так, то она останется той же, и ничего дальше считать не надо.
Если это не так, то новая точка должна лежать на пересечении новой полуплоскости и какой-то из старых. Важный факт здесь в том, что она лежит на границе новой полуплоскости. Чтобы её найти, пересечём все старые полуплоскости с этой границей и решим одномерную задачу пересечения множества интервалов, бесконечных в одну из сторон. Если получившийся интервал пуст, то и пересечение полуплоскостей пустое, а в противном случае один из его концов будет искомой точкой, если его положить обратно на границу новой полуплоскости.
Таким образом, в среднем алгоритм совершит линейное количество операций:
\[ \frac<2> <2>\cdot 2 + \frac<2> <3>\cdot 3 + \frac<2> <4>\cdot 4 + \ldots + \frac<2>
Подобная техника иногда используется и для других геометрических задач — например, для нахождения пары ближайших точек на плоскости.
ВЫПУКЛОЕ МНОЖЕСТВО
В. т. гомеоморфно замкнутому шару. Бесконечное в. т., не содержащее прямых, гомеоморфно полупространству, а содержащее прямую является цилиндром с выпуклым (возможно бесконечным) поперечным сечением.
Точка, не принадлежащая в. т., строго отделена от него гиперплоскостью, оставляющей эту точку и в. т. в разных открытых полупространствах. Два непересекающихся В. м. отделены гиперплоскостью, оставляющей их в разных замкнутых полупространствах. Последнее свойство отделимости сохраняется для В. м. в бесконечномерных векторных пространствах. С в. т. Fсвязана его опорная функция H:

При размещении начала координат внутри в. т. вводят функцию расстояния 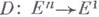

В. т. можно задавать как выпуклую оболочку точек его границы или части этих точек.
В. т. всегда имеют конечный объем (по Жордану), совпадающий с его n-мерной мерой Лебега. Граница в. т. имеет конечную ( п-1)-мерную площадь, причем различные способы введения площади в этом случае эквивалентны. Объем и площадь границы непрерывно (по метрике Хаусдорфа) зависят от в. т.
С в. т. связывают ряд простых фигур, напр, для каждого в. т. единствен наибольший (по объему) вписанный и наименьший описанный эллипсоиды [6]. Развиты признаки, выделяющие среди всех в. т. шары, эллипсоиды, центрально-симметричные тела [1], [2]. Особое место в теории В. м. занимают теоремы о семействах В. м. [6].
Значение теории В. м.- в наглядности методов и результатов, их общности и независимости от аналитич. требований гладкости (решениями экстремальных задач часто служат негладкие в. т.).
Лит.: МBonnescn Т., Fenchel W., Theorie der konvexen Кorpеr, В., 1934; [2] Valentine F., Convex sets, N. Y., 1964; [3] Дей М., Нормированные линейные пространства, пер. с англ., М., 1961; [4] Бураго Ю. Д., За л галле р В. А., Достаточные признаки выпуклости, в кн.: Вопросы глобальной геометрии, Л., 1974, с. 3-53 (Записки научных семинаров Ленинградского отделения матем. ин-та, т. 45); [5] Хадвигер Г., Лекции об объеме, площади поверхности и изопериметрии, пер. с нем., М., 1966; [6] Данцер Л., Грюнбаум Б., Кли В., Теорема Хелли и ее применения, пер. с англ., М., 1968. Ю. Д. Бурого, В. А. Залгаллер.
Проект «Выпуклая оболочка»
Этот параграф посвящен, прежде всего, решению одной конкретной задачи средней степени сложности — нахождению выпуклой оболочки последовательно поступающих точек плоскости и вычислению двух ее метрических характеристик. Дополнительная информация об этом проекте может быть найдена в книге [9].
Постановка задачи
Напомним сначала два определения, связанные с важнейшим математическим понятием — свойством выпуклости множеств.
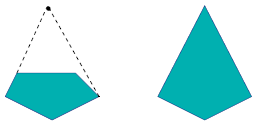
Выпуклая оболочка любого выпуклого множества совпадает с ним. Для произвольного множества выпуклая оболочка может быть получена как пересечение всех выпуклых множеств, его содержащих.
Теперь можно сформулировать основную задачу.
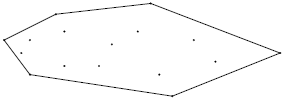
Если представить себе точки конечного множества в виде вбитых в доску гвоздей, то выпуклая оболочка — это многоугольник, форму которого принимает натянутое на гвозди резиновое кольцо (см. рис. 11.1).
Мы будем трактовать поставленную задачу следующим образом: реализовать класс Convex с методами
Договоримся придерживаться стратегии вычисления всех характеристик оболочки сразу при добавлении новой точки (в методе add ); выполнение методов perimeter и area при этом будет сводиться просто к выдаче уже вычисленных ранее значений.
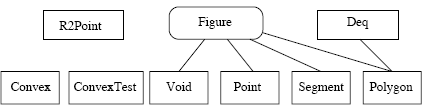
Проектирование сверху вниз
Это завершает проектирование иерархии классов, необходимой для решения поставленной задачи. Результат представлен на рис. 11.4.
Содержание:
Основные понятия:
Кантор описывает множество следующим образом:
Множество S есть любое собрание определенных и различимых между собой объектов пашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества S
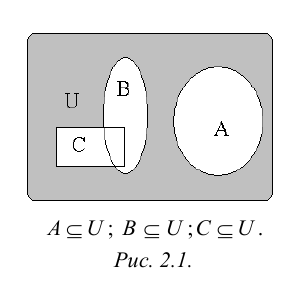
Рис. 2.1. Множество А называют подмножеством другого множества U или множество А включено во множество U, если каждый элемент множества А является одновременно элементом множества U. Это обозначается 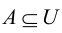
Свойства включения:
Множество, не содержащее ни одного элемента, называется пустым и обозначается 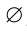
Множество 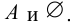
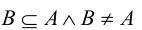
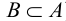
Множество всех подмножеств множества А называется множеством-степенью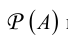
Если А не содержит элементов, т.е. 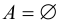
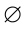
Несложно убедиться в том, что множество-степень 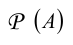
Основные операции над множествами
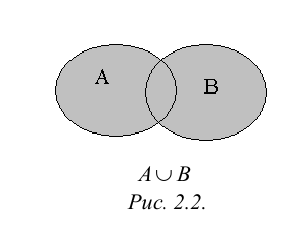
Суммой или объединением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных множеств. Эта операция над множествами обозначается знаком 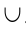
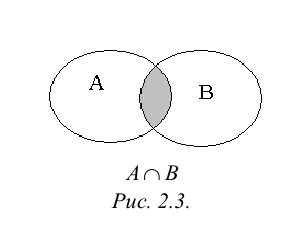
Произведением или пересечением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из заданных множеств. Эта операция над множествами обозначается знаком 
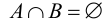
Два множества называются непересекающимися (или расчлененными) если 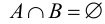
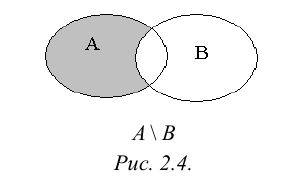
Разностью множеств А и В или дополнением В до А называется множество, состоящее только из тех элементов А, которые не входят в В. Эта операция над множествами обозначается знаком \.
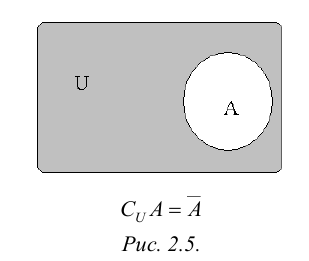
Часто все рассматриваемые множества считают подмножествами одного основного множества U. В таком случае разность U \ А (дополнение А до U) обозначают, как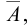
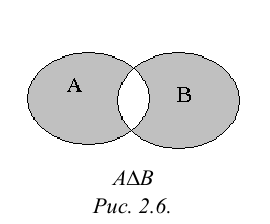
Симметрической разностью множеств А и В называется множество С: 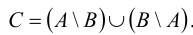
Обозначается симметрическая разность: 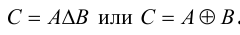
Для подмножеств данного множества U выполняются следующие законы:
Закон коммутативности (переместительный закон):
Закон ассоциативности (сочетательный закон) для любой тройки множеств А, В и С:
Закон дистрибутивности (распределительный закон) для любой тройки множеств А, В и С:
Свойства фигурируют попарно таким образом, что каждое получается из соседнего заменой 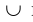

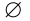
Принцип двойственности. Для любого тождества множеств двойственное ему выражение также является тождеством.
Очевидно, что операция разность не обладает свойствами коммутативности и ассоциативности, в то же время операция симметрическая разность и коммутативна, и ассоциативна.
Очевидно, что 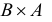
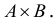
Отображения
Элемент 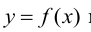
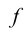
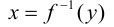
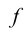
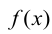
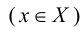
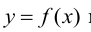
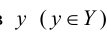
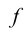
Отображение 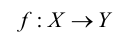
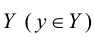
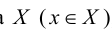
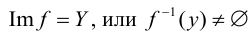
Отображение 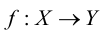
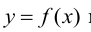
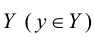
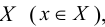
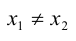
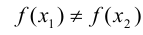
Отображение 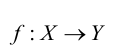
Равенство двух отображений 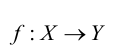
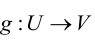
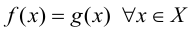
Произведение двух отображений 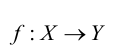
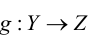
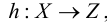
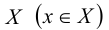
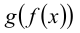
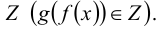
Для преобразований 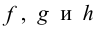
Коммутативный закон для произведения преобразований в общем случае не выполняется, т.е. 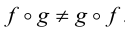
Если между двумя множествами можно задать биективное отображение (установить взаимно однозначное соответствие между их элементами), то такие множества называются эквивалентными или равномощными. Конечные множества равномощны только в том случае, когда число их элементов одинаково.
Бесконечные множества также можно сравнивать между собой.
Два множества имеют одинаковую мощность или называются эквивалентными (обозначение А = В), если между их элементами можно установить взаимно однозначное соответствие, т.е. если можно указать некоторое правило, в соответствии с которым каждому элементу одного из множеств соотносится один и только один элемент другого множества.
Если же подобное отображение невозможно, то множества имеют различную мощность; при этом оказывается, что в последнем случае, каким бы образом мы не пытались привести в соответствие элементы обоих множеств, всегда останутся лишние элементы и притом всегда от одного и того же множества, которому приписывается более высокое значение кардинального числа или говорят, что это множество имеет большую мощность.
Бесконечное множество и некоторое его подмножество могут быть эквивалентными.
Множество, эквивалентное множеству натуральных чисел, называется счетным множеством. Для того чтобы множество А было счетным, необходимо и достаточно, чтобы каждому элементу а множества А был поставлен в соответствие его порядковый номер 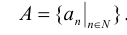
Отношения эквивалентности и упорядоченности
В математике понятие отношения используется для обозначения какой-либо связи между объектами. Отношение есть некоторое множество упорядоченных пар <х,у), где 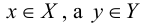
Часто приходится рассматривать несколько элементов множества как эквивалентные, потому что по определенным признакам один элемент может быть заменен другим. Так, например, по признаку величины дроби 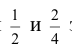
Особенности природы элементов множества в большинстве случаев позволяют установить между ними отношения полного (или совершенного) порядка. Это отношение по определению обладает следующими свойствами:
Если между элементами множества определено также и отношение эквивалентности, то между элементами устанавливается отношение неполного или нестрогого порядка:
Возможны случаи, когда некоторые элементы множества не сравнимы. Такие множества называются частично упорядоченными.
Способы задания множеств
Как в повседневной, так и в научной жизни часто говорят о чертах какого-либо коллектива, совокупности некоторых объектов. Так, например, можно говорить о студентах группы некоторого института, о совокупности точек внутри некоторого круга и т.д.
Понятие множества в математике выведено из понятия совокупностей, образуемых из предметов, сведенных в одно целое. Предметы, собранные во множество, называются элементами множества. Понятие множество и элемент считаются основным понятиями и не сведены к другим понятиям путем применения формального определения. Таким образом, под множеством, мы будем понимать любое объединение в одно целое М определенных вполне различимых объектов m из нашего восприятия или мысли, которые называются элементами М
Каждое множество считается самостоятельной осмысленной вещыо, как бы осмысленной оболочкой его элементов. Множество
считается известным, если заданы его элементы; множество определяется раз и навсегда заданием его элементов; множества не зависят or времени.
Следовательно, множество однозначно определяется его элементами.
Множество, у которого ни один предмет не является элементом, называется пустым множеством. Пустое множество обозначается символом 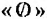
Для обозначения множеств обычно применяются заглавные латинские буквы. Выражение 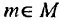
Выражение 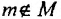
Теорема 1.1.1. Два множества тождественны (равны) тогда и только тогда. если их элементы одинаковы.
Доказательство. Если два множества тождественны (равны), то на основе понятия тождественности элементы обоих множеств одинаковы.
С другой стороны, если о двух множествах нам известно, что их элементы тождественны, то эти два множссгва тождественны, так как множество однозначно определяется его элементами.
В определениях, касающихся геометрических мест, всегда присутствует отождествление множеств, заданных двумя разнымиопределениями.
Например. Перпендикулярная липия, пересекающая отрезок прямой, является геометрическим местом точек, расположенных на одинаковом расстоянии от двух концов озрезка. Это означает следующее: В плоскости множество точек перпендикулярной линии, пересекающей в середине отрезок прямой, тождественно множеству точек, расположенных на одинаковом расстоянии от обоих концов отрезка.
Множество часто задается в следующем виде: элементы множества заключаются внутри фигурных скобок: <. >. Подобной записью может быть конкретное перечисление элементов множества или задание такого определения, которым элементы множества однозначно задаются.
Заметим, что один предмет в одном множестве является элементом только один раз, даже если предмет повторяется несколько раз.
Тождественные множества связываются знаком равенства (=):
Множество А считается подмножеством В, если каждый элемент А является и элементом В, что обозначается выражением 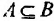
Понятие части (подмножества) в теории множеств отличается от обычного понятия части. В обычном понимании часть всегда меньше целого. А по понятию части в теории множеств целое также входит в понятие части, т.е. каждое множество является элементом самого себя, гак как каждый элемент А является элементом А, значит 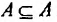
Множество А является действительным подмножеством множества B, если А является частью В, но не тождественно с ним, что обозначается 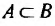
Примеры:
Не существует никакого ограничения в отношении того, насколько много (или мало) элементов может быть в одном множеств: в одном множестве может быть любое, даже бесконечное количество элементов.
Сравнивать множества можно, используя понятие взаимно однозначного соответствия между элементами.
Если каждому элементу множества А по некоторому закону ставится в соответствие определенный элемент множества В и если при этом каждый элемент множества В оказывается поставленным в соответствие одному и только одному элементу множества А, то говорят, что между А и В установлено взаимно однозначное соответствие.
Особую роль в теории множеств играет универсальное множество, которое часто называют просчранством. Это некоторое множество, фиксированное в рамках данной математической теории и содержащее в качестве элементов все объекты, рассматриваемые в этой теории.
Алгебраические операции над множествами
Определим операции, выполняемые над множествами.
а) Пересечением множеств Ми N называется множество, которое будет обозначаться М 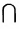
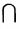
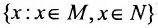
Эта запись означает, что пересечение M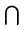
N. Например, если М = <0,1,2,3>, а N = <1,4,3,6>, то М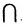
Если А 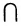
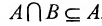
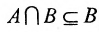
А 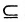
Вели 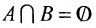
А и Б называются посторонними множествами.
Если есть совокупность множеств 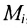
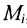
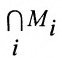
принадлежащих одновременно всем множествам совокупности 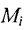
6) Объединением двух множеств А и В называется множество A 
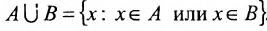
Эта запись означает, что объединение A 
Легко увидеть, что если А и В являются ограниченными множествами без общих элементов, то количество элементов A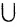
Так же действительны соотношения: 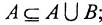
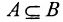
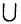
В общем случае, когда имеется совокупность множеств 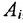
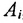
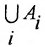
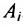
в) Множество элементов Е, не принадлежащих некоторой его части А, называется дополнением (разностью) к А в Е и обозначается через 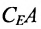
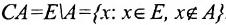
Для операции разности справедливы следующие соотношения:
г) Произведением А х В двух множеств А и В называется множество всевозможных упорядоченных пар (а, Ь), образованных из элементов а множества А и элементов b множества В, т.е. 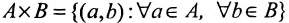
Пары (а, b) и (b, а) с 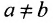
Пример:
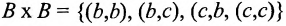
Справедливы следующие операции для декартового произведения множеств:
Понятие множества широко используется в экономических исследованиях. Так при изучении системы производства одного предприятия или нескольких, которые потребляют продукты: сырьё, энергию и трудовые ресурсы и производят в соответствии с некоторой технологией другие продукты-изделия, составляется математическая модель, где используется множество
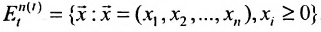
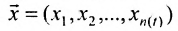
Выпуклые множества. Пересечение выпуклых множеств
В первом пункте мы определили множество, указали способы его задания. Теперь мы укажем некоторые дополнительные свойства множеств. Для этого введем ряд определений.
Окрестностью точки 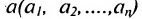
точек 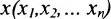
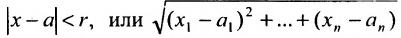
Таким образом, окрестность образуют все точки х, удаленные от точки а на расстояние меньшее r.
Точка 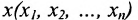
Точка пространства называется внешней по отношению к некоторому множеству точек, если она с некоторой окрестностью не принадлежит этому множеству.
Точка пространства называется граничной, если в любой её окрестности имеются точки как принадлежащие множеству так и не принадлежащие ему. Множество, содержащее все граничные точки, называется замкнутым.
Например, отрезок является замкнутым множеством.
Множество (тело) называется выпуклым, если оно вместе со своими двумя любыми точками Р и Q содержит все точки отрезка 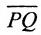
Примером выпуклого множества может служить отрезок. Из геометрии известны фигуры: треугольник, квадрат, прямоугольник, ромб, круг, эллипс. Множества точек, ограниченные эти фигурами, являются выпуклыми. В пространстве выпуклыми множествами являются: шар, эллипсоид, конус, цилиндр и другие.
Для выпуклых множеств, справедлива следующая теорема.
Теорема 1.3.1. Пересечение выпуклых множеств (тел) есть выпуклое множество, если оно не пусто.
Доказательство. Пусть имеется не пустое пересечение выпуклых множеств. Возьмём две произвольные точки Р u Q, принадлежащие этому пересечению. По определению пересечения эти точки принадлежат каждому из множеств, а так как эти множества выпуклы, то вместе с точками Р и Q им принадлежат и все точки отрезка PQ. Следовательно, все точки отрезка PQ принадлежат и пересечению, что и доказывает его выпуклость.
Точка множество называется крайней, если она не является внутренней ни для какого отрезка, целиком принадлежащего множеству.
Так у выпуклого многоугольника крайними точками являются его вершины. Их конечное число. В пространстве многогранником называется множество с конечным числом крайних точек. Следовательно. выпуклый многогранник является замкнутым выпуклым множеством.
Высказывание
Математическая логика является современной формой так называемой формальной логики, применяющей математические методы для исследования своего предмета. В формальной логике и, соответственно, математической логике, собраны результаты законов структуры правильных выводов. Вывод является таким мыслительным процессом, в результате которого появляются новые открытия на основании уже имеющихся, без практических исследований. Рассмотрим пример вывода:
Предпосылки: Если будет раздача премии, то мы выполним план.
Будет раздача премии.
Окончательные выводы: Мы выполним план.
Если принять правильность предпосылок, то следует принять и правильность окончательного вывода. Обычно вместо предложений могут быть записаны любые такие изъявительные предложения, значения которых может быть правильно или ложно; следует оставить неизменённым только расположение слов «если» и «то» и расположение предложений, то есть структуру вывода. Структуру вывода можно выразить следующей схемой:
Путем изменения условий могут быть построены различные теории логики. Важнейшими главами математической логики является калькуляция высказываний и калькуляция предикатов.
Определение 1.4.1. Под термином высказывания подразумевается такое изъявительное предложение, которое является однозначно или правильным, или ложным.
Высказывание удовлетворяет условиям:
Следовательно, каждое высказывание имеет значение 1 (истинно) или 0 (ложно).
В выводах могут фигурировать высказывания (либо в виде предпосылок, либо как окончательный вывод), возникшие из одного или нескольких высказываний, путем применения некоторого грамматического метода; они называются сложными высказываниями.
Определение 1.4.2. Под термином калькуляция высказываний подразумевается такой метод, с помощью которого из одного или нескольких высказываний получается такое высказывание, правильность или ложность которого однозначно определяется правильностью или ложсностью членов.
Операции над высказываниями
Отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность
Простейшими примерами операций калькуляции высказываний является отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность и т.д.
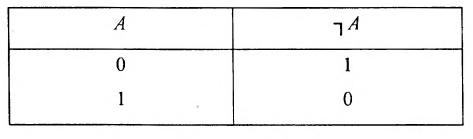
Определение 1.5.1. Под отрицанием высказывания А подразумевается высказывание «Неправильно, что А» или некоторая грамматически преобразованая форма данного высказывания.
По значению выражения «неправильно» отрицание А правильно тогда и только тогда, если самоё А неправильно; следовательно, отрицание действительно есть операция калькуляции высказываний.
Например: отрицание предложения «мотор работает» является предложение «мотор не работает».
Отрицание является (унарной) одночленной операцией. Отрицание А обозначается символом 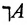
Закон двойного отрицания: 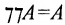
Здесь и в дальнейшем свойство высказываний «правильное» и «ложное» называется логическими значениями и обозначается 1 и О (п. и л.). Тогда операции, проводимые на логических значениях, называются логическими операциями. Для выражения любых логических значений вводятся логические переменные; они обозначаются символами 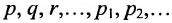
Следовательно, логические переменные могут принимать два значения 1 или 0. При использовании нескольких операций последовательно порядок выполнения отдельных операций обозначается скобками.
В общем случае, n-члснной логической операцией называется каждая такая функция, областью существования которой является упорядоченное множество всех выражений, образуемых из логических значений 1 и 0 с длиной выражения n, а значением её является одно из двух логических значений 1 и 0.
Определение 1.5.2. Под конъюнкцией двух высказываний А и В подразумевается высказывание «А и В».
По значению союза «и» конъюнкция является правильной тогда и только тогда, если оба её члена правильны, т.е. используя логические переменные можно записать:
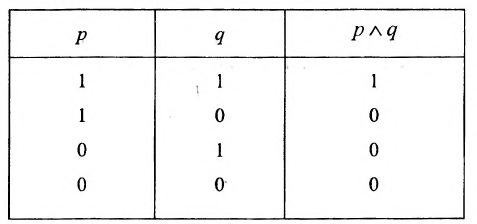
Таблица значений конъюнкции имеет вид:
Теорема 1.5.1. Любая логическая операция может быть выражена через операции отрицания и конъюнкции.
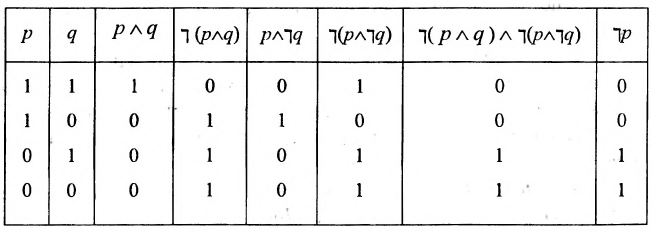
В области логических операций для контроля любого тождества составляется общая таблица операций, представленных по обеим сторонам знака =. Результат операций указывается в столбцах.
Пример:
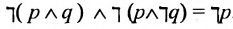
Решение:
Доказательство данного равенства проведём в табл. 3:
Определение 7.5.3. Под дизъюнкцией двух высказываний А и В подразумевается высказывание «А или В».
По значению союза «или» дизъюнкция является ложной, если оба её члена ложны, т.е. используя логические переменные можно записать:
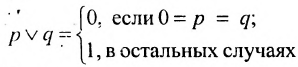
Дизъюнкция выражается с помощью операции конъюнкции и отрицания б следующей форме:
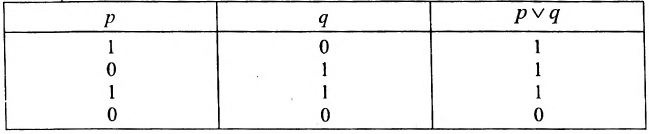
Таблица значений дизъюнкции имеет следующий вид:
По аналогии с теоремой 3 можно сформулировать следующую теорему
Теорему 1.5.2. Каждая логическая операция может быть выражена с помощью только операций дизъюнкции и отрицания.
Например, операция конъюнкции выражается с помощью операций дизъюнкции и отрицания в виде: 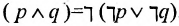
Определение 1.5.4. Операция, обозначаемая 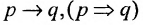
называется импликацией (с предварительным членом р и с последующим q).
Иначе её обозначение 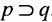
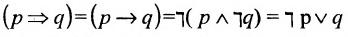
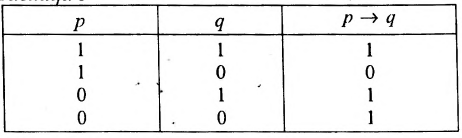
Таблица значений импликации имеет следующий вид: Таблица 5
И конъюнкция, и дизъюнкция выражаются с помощью операций импликации и отрицания: 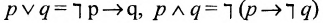
Поэтому любая логическая операция может быть выражена ( помощью операций импликации и отрицания.
Выражения вида: «если А, то В», «неправильно, что: А и не В» «В если только А», «только тогда А, если В», «Достаточным условием В является А», «Необходимым условием А является В» соответственно обозначаются А 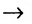

Определение 1.5.5. Операция, обозначаемая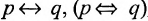
называется эквивалентностью (читается р эквивалентно q). Выражениями данной операции являются следующие:
Так как высказывание 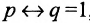
p=q, то данная логическая операция соответствует образованию
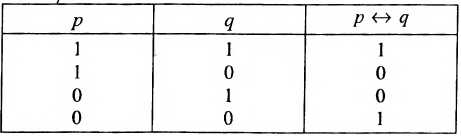
сложного предложения вида «А тогда и только тогда, когда В». Таблица значений эквивалентности имеет вид:
1) операция взаимоисключающего или (р или же q): 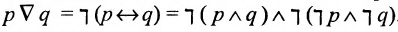
2) операция «ни-ни» (обозначается 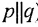
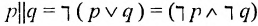
Предикаты и кванторы
Кроме заполнения оставленных свободных мест названиями имеется и другой способ образования высказываний из предикатов: квантификация. Например, из открытого предложения «если х представляет собой дифференцируемую функцию, то функция х-непрерывная функция», подставив перед предложением «Для каждого л», получим следующее: Для каждого х, если х представляет собой дифференцируемую функцию, то x представляет собой непрерывную функцию. Текст «Для каждого x» обозначается символом 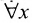
Существует ещё экзистенциальный квантор, который заменят текст «Имеется такое х» или «Существует такое х» и обозначается 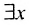
Для точного анализа вводятся следующие понятия:
Предикаты обозначаются символами 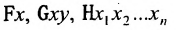
Жирными буквами обозначаются предикаты, а строчными буквами- аргументы предиката как функции; количеством последних определяется размерность предиката.
Например. Пусть Н- множество натуральных чисел, тогда предикат неделимого числа Fx определяется следующим образом:
Множества, операции над ними
Понятие множества является одним из основных в математике. Оно принадлежит к числу первичных, не определяемых через более простые.
Под множеством будем понимать совокупность объектов, объединенных по какому-либо признаку. Слова «совокупность», «набор», «система», «объединение» и другие являются синонимами слова «множество». Например, можно говорить о множестве студентов в институте, множестве букв в алфавите, множестве целых чисел и т. д. Из приведенных примеров следует, что множество может содержать как конечное, так и бесконечное число объектов некоторой природы. Объекты, из которых состоит множество, называются его элементами или точками. Принадлежность элемента 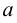
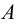
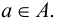
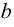
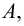
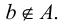
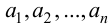
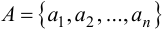
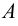
Два множества 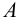
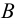
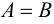
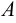
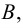
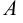
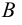
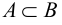
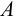
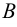
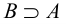
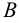
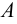
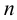
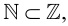
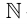
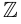
Множество, не содержащее ни одного элемента, будет называться пустым множеством и обозначаться 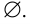
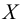
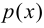
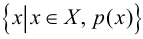
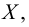
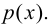
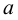
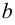
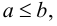
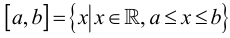
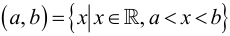
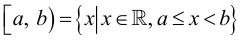
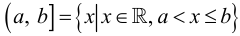
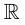
Пересечением множеств 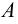
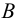
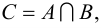
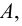
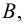
Объединением множеств 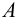
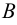
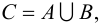
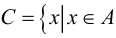
Разностью множеств 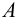
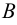
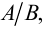
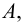
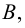
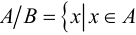
Пусть 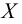
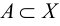
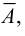
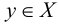
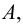
Таким образом, все элементы, которые не принадлежат множеству 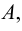
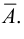
Логические символы
Часто используются также логические символы следствия 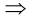
Грани числовых множеств
Говорят, что множество 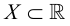
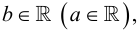
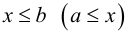
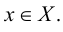
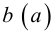
Множество, ограниченное и сверху, и снизу, называется ограниченным, т. е. существуют два числа 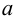
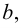
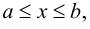
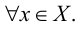
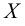
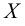
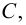
Множество, не ограниченное сверху или снизу, называется неограниченным.
Если число 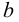
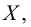
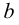
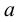
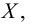
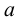
Наименьшая (наибольшая) из всех верхних (нижних) граней называется точной верхней (нижней) гранью множества и обозначается символом 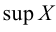
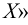
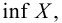
Точные верхняя и нижняя грани множества могут принадлежать или не принадлежать этому множеству. Если множество 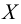
Теорема 1*. Всякое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.
Предельные точки числового множества. Открытые и замкнутые множества
Множество вещественных чисел 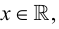
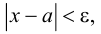
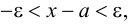
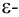
Множество вещественных чисел 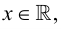
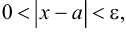
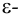
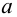
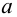
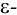
Геометрически 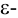
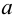
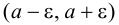
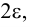
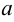
Точка 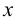
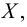
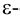
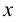
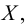
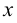
Точка 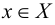
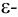
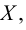
Точка 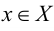
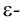
Точка 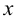
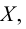
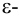
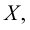
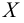
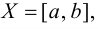
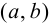
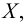
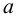
Если множество 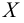
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.