Что такое выражение пример

Числовые и буквенные выражения

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Числовые выражения: что это

Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

Это простые числовые выражения.

Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

Это сложные числовые выражения.

Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

14 больше 4
14 > 4
6 + 8 > 2 * 2

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

Пример 1. Найдите значение выражения: 5 + x.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

Выражения с переменными

Переменная — это значение буквы в буквенном выражении.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a

Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Задание раз.

Задание два.

Составьте буквенное выражение:

Сумма разности b и 345 и суммы 180 и x.

Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.

Ответ: Маша и Лена посмотрели всего 313 видео.

Источник

Что такое числовые выражения

Содержание статьи

Отличительной особенностью выражения является наличие математических действий. Оно обозначаются определенными знаками (умножения, деления, вычитания или сложения). Последовательность выполнения математических действий при необходимости корректируется скобками. Выполнить математические действия – значит найти значение выражения.

Что не является выражением

Не всякую математическую запись можно отнести к числу выражений.

Равенства не являются выражениями. Присутствуют при этом в равенстве математические действия или нет, не имеет значения. Например, a=5 – это равенство, а не выражение, но и 8+6*2=20 тоже нельзя считать выражением, хотя в нем и присутствуют умножение и сложение. Этот пример тоже принадлежит к категории равенств.

Понятия выражения и равенства не являются взаимоисключающими, первое входят в состав второго. Знак равенства соединяет два выражения:
5+7=24:2

Можно это равенство упростить:
5+7=12

Выражение всегда предполагает, что представленные в нем математические действия могут быть выполнены. 9+:-7 – это не выражение, хотя здесь есть знаки математических действий, ведь выполнить эти действия невозможно.

Существуют и такие математические примеры, которые формально являются выражениями, но не имеют смысла. Пример такого выражения:
46:(5-2-3)

Число 46 необходимо разделить на результат действий в скобках, а он равен нулю. На нуль же делить нельзя, такое действие в математике считается запретным.

Числовые и алгебраические выражения

Существует два вида математических выражений.

Если выражение содержит только числа и знаки математических действий, такое выражение называется числовым. Если же в выражении наряду с числами присутствуют переменные, обозначаемые буквами, или чисел нет вообще, выражение состоит только из переменных и знаков математических действий, оно называется алгебраическим.

Принципиальное отличие числового значения от алгебраического состоит в том, что у числового выражения значение только одно. Например, значение числового выражения 56–2*3 всегда будет равно 50, ничего изменить нельзя. У алгебраического же выражения значений может быть много, ведь вместо буквы можно подставить любое число. Так, если в выражении b–7 вместо b подставить 9, значение выражения будет равно 2, а если 200 – оно будет составлять 193.

Источник

Числовые и алгебраические выражения. Преобразование выражений.

Что такое выражение в математике? Зачем нужны преобразования выражений?

Допустим, перед вами злой пример. Очень большой и очень сложный. Допустим, вы сильны в математике и ничего не боитесь! Сможете сразу дать ответ?

Вам придётся решать этот пример. Последовательно, шаг за шагом, этот пример упрощать. По определённым правилам, естественно. Т.е. делать преобразование выражений. Насколько успешно вы проведёте эти преобразования, настолько вы и сильны в математике. Если вы не умеете делать правильные преобразования, в математике вы не сможете сделать ни-че-го.

Во избежание такого неуютного будущего (или настоящего. ), не мешает разобраться в этой теме.)

Для начала выясним, что такое выражение в математике. Что такое числовое выражение и что такое алгебраическое выражение.

Что такое выражение в математике?

В общем виде термин «математическое выражение» применяется, чаще всего, чтобы не мычать. Спросят вас, что такое обыкновенная дробь, например? И как ответить?!

Первый вариант ответа: «Это. м-м-м-м. такая штука. в которой. А можно я лучше напишу дробь? Вам какую?»

Второй вариант как-то посолидней будет, правда?)

Вот в этих целях фраза «математическое выражение» очень хороша. И правильно, и солидно. Но для практического применения надо хорошо разбираться в конкретных видах выражений в математике.

Числовые выражения.

Что такое числовое выражение? Это очень простое понятие. Само название намекает, что это выражение с числами. Да, так оно и есть. Математическое выражение, составленное из чисел, скобок и знаков арифметических действий называется числовым выражением.

тоже числовое выражение, да.

Когда числовое выражение не имеет смысла?

Понятное дело, если мы видим перед собой какую-то абракадабру, типа

то делать ничего и не будем. Так как непонятно, что с этим делать. Бессмыслица какая-то. Разве что, посчитать количество плюсиков.

Но бывают внешне вполне благопристойные выражения. Например такое:

Чтобы дать такой ответ, пришлось, конечно, посчитать, что в скобочках будет. А иногда в скобочках такого понаворочено. Ну тут уж ничего не поделаешь.

Алгебраические выражения.

и так далее, до бесконечности. )

В арифметике можно записать, что

А вот если мы подобное равенство запишем через алгебраические выражения:

мы сразу решим все вопросы. Для всех чисел махом. Для всего бесконечного количества. Потому, что под буквами а и b подразумеваются все числа. И не только числа, но даже и другие математические выражения. Вот так работает алгебра.

Когда алгебраическое выражение не имеет смысла?

Про числовое выражение всё понятно. Там на ноль делить нельзя. А с буквами, разве можно узнать, на что делим?!

Возьмём для примера вот такое выражение с переменными:

Конечно. Просто в таких случаях говорят, что выражение

имеет смысл для любых значений а, кроме а = 5.

Весь набор чисел, которые можно подставлять в заданное выражение, называется областью допустимых значений этого выражения.

Как видите, ничего хитрого нет. Смотрим на выражение с переменными, да соображаем: при каком значении переменной получается запретная операция (деление на ноль)?

А потом обязательно смотрим на вопрос задания. Чего спрашивают-то?

Если спрашивают, при каком значении переменной выражение не имеет смысла, наше запретное значение и будет ответом.

Если спрашивают, при каком значении переменной выражение имеет смысл (почувствуйте разницу!), ответом будут все остальные числа, кроме запретного.

Зачем нам смысл выражения? Есть он, нет его. Какая разница?! Дело в том, что это понятие становится очень важным в старших классах. Крайне важным! Это основа для таких солидных понятий, как область допустимых значений или область определения функции. Без этого вы вообще не сможете решать серьёзные уравнения или неравенства. Вот так.

Преобразование выражений. Тождественные преобразования.

Мы познакомились с числовыми и алгебраическими выражениями. Поняли, что означает фраза «выражение не имеет смысла». Теперь надо разобраться, что такое преобразование выражений. Ответ прост, до безобразия.) Это любое действие с выражением. И всё. Вы эти преобразования делали с первого класса.

Возьмём крутое числовое выражение 3+5. Как его можно преобразовать? Да очень просто! Посчитать:

Вот этот расчёт и будет преобразованием выражения. Можно записать то же самое выражение по-другому:

Тут мы вообще ничего не считали. Просто записали выражение в другом виде. Это тоже будет преобразованием выражения. Можно записать вот так:

Любое действие над выражением, любая запись его в другом виде называется преобразованием выражения. И все дела. Всё очень просто. Но есть здесь одно очень важное правило. Настолько важное, что его смело можно назвать главным правилом всей математики. Нарушение этого правила неизбежно приводит к ошибкам. Вникаем?)

Предположим, мы преобразовали наше выражение как попало, вот так:

Преобразование? Конечно. Мы же записали выражение в другом виде, что здесь не так?

Всё не так.) Дело в том, что преобразования «как попало» математику не интересуют вообще.) Вся математика построена на преобразованиях, в которых меняется внешний вид, но суть выражения не меняется. Три плюс пять можно записать в каком угодно виде, но это должно быть восемь.

Преобразования, не меняющие сути выражения называются тождественными.

Именно тождественные преобразования и позволяют нам, шаг за шагом, превращать сложный пример в простое выражение, сохраняя суть примера. Если в цепочке преобразований мы ошибёмся, сделаем НЕ тождественное преобразование, дальше мы будем решать уже другой пример. С другими ответами, которые не имеют отношения к правильным.)

Вот оно и главное правило решения любых заданий: соблюдение тождественности преобразований.

Пример с числовыми выражением 3+5 я привёл для наглядности. В алгебраических выражениях тождественные преобразования даются формулами и правилами. Скажем, в алгебре есть формула:

Как вы, наверняка, догадались, эту цепочку можно продолжать до бесконечности. ) Очень важное свойство. Именно оно позволяет превращать всякие монстры-примеры в белые и пушистые.)

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Нахождение значения выражения: правила, примеры, решения

В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.

Как найти значение числового выражения?

Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.

Простейшие случаи

Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.

Пример 1. Значение числового выражения

Выполним сначала умножение и деление. Получаем:

Теперь проводим вычитание и получаем окончательный результат:

Сначала выполняем преобразование дробей, деление и умножение:

Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:

Искомое значение найдено.

Выражения со скобками

Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.

Пример 3. Значение числового выражения

Значение выражений, содержащих скобки в скобках, находится по такому же принципу.

Пример 4. Значение числового выражения

Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.

Выражения с корнями

Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.

Пример 5. Значение числового выражения

Сначала вычисляем подкоренные выражения.

Теперь можно вычислить значение всего выражения.

Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.

Пример 6. Значение числового выражения

Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.

Выражения со степенями

Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.

Пример 7. Значение числового выражения

Начинаем вычислять по порядку.

Осталось только провести операцию сложение и узнать значение выражения:

Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.

Пример 8. Значение числового выражения

Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.

Выражения с дробями

Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.

Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.

Пример 9. Значение числового выражения

Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.

Перепишем наше выражение и вычислим его значение:

Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.

Пример 10. Значение числового выражения

Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.

Исходное выражение принимает вид:

Вычислим значение этого выражения:

Выражения с логарифмами

Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.

Пример 11. Значение числового выражения

По свойству логарифмов:

Вновь применяя свойства логарифмов, для последней дроби в выражении получим:

Теперь можно переходить к вычислению значения исходного выражения.

Выражения с тригонометрическими функциями

Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.

Пример 12. Значение числового выражения

Сначала вычисляем значения тригонометрических функций, входящих в выражение.

Подставляем значения в выражение и вычисляем его значение:

Значение выражения найдено.

Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.

Пример 13. Значение числового выражения

Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.

Общий случай числового выражения

В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.

Как найти значение выражения

Пример 14. Значение числового выражения

Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?

Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.

π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π

Теперь можно узнать значение синуса:

Вычисляем значение подкоренного выражения:

2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4

Со знаменателем дроби все проще:

Теперь мы можем записать значение всей дроби:

С учетом этого, запишем все выражение:

В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.

Вычисление значений выражений рациональными способами

Нахождение значений выражений с переменными

Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.

Нахождение значений выражений с переменными

Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.

Подставляем значения переменных в выражение и вычисляем:

Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.

Еще один пример. Значение выражения x x равно единице для всех положительных иксов.

Источник

Числовые выражения и буквенные выражения — правила

При решении примеров и уравнений нужно четко отличать — что такое числовые выражение, а что такое буквенные выражения. Поэтому сегодня пройдем эту тему и посмотрим видео. Итак, выучите правила.

Правила математики о числовых и буквенных выражениях

Число, которое получается в результате выполнения математических операций, входящих в это числовое выражение, называется значением числового выражения.

Числа, которые заменяют букву, называются значениями этой буквы.

Чтобы запомнить правила, давайте обратимся к примерам. Примеры — самый простой наглядный способ запомнить утверждения, приведенные выше.

Примеры числовых выражений

— в левой части этого равенства стоит числовое выражение, а в правой части — значение числового выражения.

— в левой части равенства — числовое выражение, а в правой части — значение числового выражения.

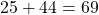
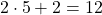
Посмотрите еще примеры числовых выражений:

Примеры буквенных выражений

Примеры буквенных выражений:

Буквенных выражений может быть множество. Для буквенных выражений каждая буква — это определенное число. Или множество разных чисел.

Когда применяются буквенные выражения

Буквенные выражения применяются тогда, когда нам надо, например, ввести формулу для нахождения той или иной величины. Например, вы знаете — что периметр прямоугольника, это сумма всех его сторон. Для периметра в общем виде можно записать буквенное выражение:

, где — ширина прямоугольника, а — его длина.

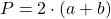
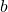
В правой части вы увидели буквенное выражение, значениями букв и — будут числа — значения ширины и длины прямоугольника.

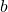
Математические выражения

— это математическое выражение.

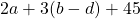
Число перед буквой в математическом выражении — это коэффициент, означающий, что это число умножается на букву, которая может иметь переменное значение.

Буквенные, числовые и математические выражения — необходимо различать, чтобы понимать условия задачи, например, вас могут попросить упростить математическое выражение или попросить найти значение числового выражения. Поэтому необходимо знать — что это такое.

Источник