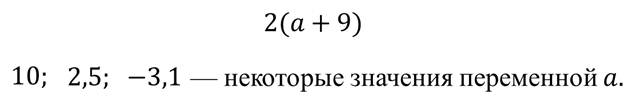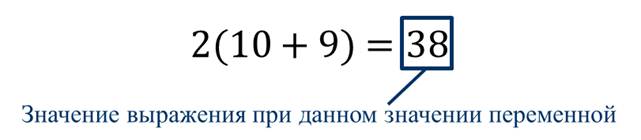Что такое выражение с переменной 7 класс алгебра

Числовые, буквенные выражения и выражения с переменными: определения, примеры

В математике принято использовать свои обозначения. Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.

Числовые выражения

Конечно, числовые выражения содержат не только знаки «плюс» и «минус». Они могут включать деление и умножение, содержать скобки, степени, корни, логарифмы и состоять из нескольких действий.

Учитывая все сказанное, дадим определение. Что такое числовое выражение?

Определение. Числовое выражение

Числовым выражением считается только та комбинация, которая составлена с учетом математических правил.

Поясним данное определение.

Во-первых, числа. Математическое выражение может содержать любые числа. Это значит, что в математическом выражении можно встретить:

деление в выражениях может присутствовать как в виде знака, так и в виде дробной черты.

Скобки в числовых выражениях

Согласно определению, числовые выражения могут содержать степени, корни, логарифмы, тригонометрические и обратные тригонометрическим функции. Приведем пример такого числового выражения:

В качестве примера использования в числовых выражениях специальных знаков, можно привести знак модуля.

Буквенные выражения

После знакомства с числовыми выражениями можно вводить понятие буквенных выражений. Интуитивно понятно, что в них вместо чисел используются буквы. Но обо всем по порядку.

Запишем числовое выражение, но вместо одного числа оставим пустой квадратик.

Определение. Буквенное выражение

Выражение, в котором буквы заменяняют некоторые цифры, называется буквенным выражением. Буквенное выражение должно содержать по крайней мере одну букву.

Приведем пример сложного буквенного выражения.

Выражения с переменными

В рассмотренных выше буквенных выражениях буква обозначала какое-то конкретное числовое значение. Величина, которая может принимать ряд различных значений, называется переменной. Выражение с такой величиной, соответственно, называются выражением с переменной.

Определение. Выражения с переменными

Вообще буквенные выражения и выражения с переменными позволяют посмотреть на задачу вне контекста конкретных чисел, то есть более широко. Они широко используются в математическом анализе для формулировок и доказательств.

Внешний вид буквенного выражения не позволяет узнать, являются входящие в него буквы переменными, или нет. Для этого нужно знать условия конкретной задачи, описываемой выражением. Вне контекста ничто не мешает считать входящие в выражение буквы переменными. Таким образом, разница между понятиями «буквенное выражение» и «выражение с переменными» нивелируется.

Источник

Выражения с переменными

Урок 2. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Выражения с переменными»

· ввести понятие «выражение с переменными»;

· ввести понятие «область определения выражения».

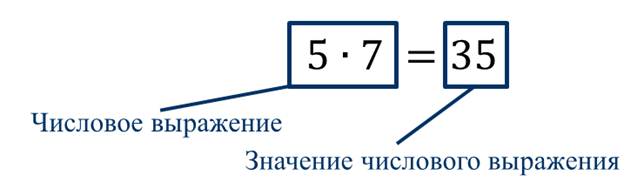
Вспомним, что на прошлом уроке мы говорили о числовых выражениях и значениях числовых выражений.

Числовым выражением называется запись, составленная из чисел, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.

Значением числового выражения называется число, которое получается при выполнении всех действий числового выражения.

Буквенным выражением называется запись, состоящая из чисел, букв, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.

Строчные буквы латинского алфавита чаще всего используют при записи буквенных выражений.

Следует также знать, что и одна буква является буквенным выражением.

Давайте решим задачу.

Велосипедист двигается со скорость 15 километров в час. Какой путь он проедет за время t?

Известно, что путь можно найти скорость умножив на время. Тогда путь, который проедет велосипедист, будет равен 15t.

Теперь, если нам нужно будет узнать, какое расстояние проехал велосипедист, например, за 3 часа, мы подставим в выражение 15 ∙ t вместо буквы t число 3, то есть найдём значение выражения при t = 3, и получим 45 километров.

В нашем случае буква t называется переменой, а само выражение – выражением с переменной.

То есть, переменная – это буква, входящая в буквенное выражение, которая может принимать различные значения.

Если мы в выражение с переменной вместо переменной подставим число, то получим числовое выражение.

Теперь, прежде, чем перейти к решению упражнений, вернёмся к выражению 15t, которое мы получили при решении первой задачи. Здесь переменная t может принимать только положительные значения, так как время не может быть отрицательным, и это множество значений называется областью определения выражения 15t.

Таким образом, важно помнить, что в область определения любого выражения могут входить только те значения переменных, при которых получается числовое равенство, имеющее смысл.

А сейчас давайте решим некоторые упражнения.

Источник

Конспект урока по теме «Выражения с переменными» ( 7 класс)

Тема . Выражения с переменными.

Проверка домашнего задания.

Актуализация опорных знаний .

1. Теоретический опрос фронтально. (работа с учебником)

Что называется числовым выражением?

2. Для чего в записи числового выражения присутствуют скобки?

3. Когда числовое выражение имеет смысл? Приведите пример такого выражения.

4. Когда числовое выражение не имеет смысла? Приведите пример такого выражения.

5. Что называется значением числового выражения?

6. Каков порядок выполнения действий при нахождении значения числового выражения?

7. Как выразить 15% в виде обыкновенной и десятичной дроби?

1. Назовите числовые выражения, не имеющие смысла: №13

2. Найдите значение числового выражения. №1

Объяснение нового материала.

Выражения с переменными.

1. Мотивация изучения.

При решении многих практических задач удобно для обозначения различных чисел использовать буквы.

Например, если a и b – длины сторон прямоугольника, то выражение a ∙ b показывает способ вычисления его площади и т.д.

Если в числовом выражении некоторые (или все) входящие в него числа заменить буквами, то получим выражение с переменными (переменной).

3. Нахождение значения выражения с переменной.

Определение 2 . Чтобы найти значения выражения с переменной надо:

1) Подставить вместо переменных их значения;

2) Найти числовое значение.

4. Допустимые значения переменных.

Пример 3. Найдите допустимые значения переменной:

1) 3х – 27. Ответ : х – любое число.

2) ; Для этого найдем, при каком значении х знаменатель обращается в нуль:

Формирование умений и навыков.

1) если х = – 6,8, то – 6,8 + 3,2 = – 3,6;

2) если х = – 3,2, то – 3,2 + 3,2 = 0;

Уч.с.9 № 21. Найдите значения выражений 10 – 2у и 10 + 2у и запишите их в соответствующие клетки таблицы:

*Уч.с.10 № 26(б). Известно, что при некоторых значениях х и у значение выражения х – у равно 0,7. Какое значение принимает при тех же х и у выражение: б) у – х.

б) если х – у = 0,7, то у – х = – (х – у) = – 0,7.

Уч.с.10 № 29. Опытное поле разбили на два участка. Площадь первого участка а га, а второго b га. С каждого гектара первого участка собрали 32 ц пшеницы, а с каждого гектара второго участка собрали 40 ц пшеницы. Сколько пшеницы собрали с обоих участков? Вычислите при а = 120, b = 80.

S ₂ = b га, собрали по 40 ц с каждого га

32 ∙ 120 + 40 ∙ 80 = 3840 + 3200 = 7040 (ц). Ответ : 7040 ц.

Подведение итогов урока.

Что называется выражением с переменной?

Может ли выражение состоять из одной буквы? А числа?

Как найти значение выражения с переменной при определенном значении переменной?

Какие способы записи можно использовать при нахождении значения выражения с переменной?

Домашнее задание. п. 2 (выучить теорию). № 20, 24(а,в)**, 30,39

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Тема. «Выражения с переменными.»

Цель. Ввести понятия «переменная», «выражение с переменной», «числовое значения выражения с переменной; формировать умение находить значение выражения с переменной, используя различные формы записи («если …, то …» таблица).

Ход урока.

1. Теоретический опрос фронтально. (работа с учебником)

2. Для чего в записи числового выражения присутствуют скобки?

3. Когда числовое выражение имеет смысл? Приведите пример такого выражения.

4. Когда числовое выражение не имеет смысла? Приведите пример такого выражения.

5. Что называется значением числового выражения?

6. Каков порядок выполнения действий при нахождении значения числового выражения?

7. Как выразить 15% в виде обыкновенной и десятичной дроби?

2. Устная работа.

1. Назовите числовые выражения, не имеющие смысла: №13

2. Найдите значение числового выражения. №1

Выражения с переменными.

1. Мотивация изучения.

При решении многих практических задач удобно для обозначения различных чисел использовать буквы.

Например, если a и b – длины сторон прямоугольника, то выражение a ∙ b показывает способ вычисления его площади и т.д.

2. Определение.

Если в числовом выражении некоторые (или все) входящие в него числа заменить буквами, то получим выражение с переменными (переменной).

Определение 1. Выражения с переменными – выражения, состоящие из переменных, чисел и знаков действий. (записать в тетрадь)

Пример 1.;.

3.Нахождение значения выражения с переменной.

Определение 2. Чтобы найти значения выражения с переменной надо:

1) Подставить вместо переменных их значения;

2) Найти числовое значение.

Пример 2. Найти значение выражения №19(а) устно,(б) письменно.

4. Допустимые значения переменных.

Определение 3. Допустимыми значениями называют те значения переменных, при которых выражение имеет смысл.

Пример 3.Найдите допустимые значения переменной:

1) 3х – 27. Ответ: х – любое число.

2) ; Для этого найдем, при каком значении х знаменатель обращается в нуль:

1) если х = – 6,8, то – 6,8 + 3,2 = – 3,6;

2) если х = – 3,2, то – 3,2 + 3,2 = 0;

Уч.с.9 № 21.Найдите значения выражений 10 – 2у и 10 + 2у и запишите их в соответствующие клетки таблицы:

*Уч.с.10 № 26(б). Известно, что при некоторых значениях х и у значение выражения х – у равно 0,7. Какое значение принимает при тех же х и у выражение: б) у – х.

б) если х – у = 0,7, то у – х = – (х – у) = – 0,7.

Уч.с.10 № 29.Опытное поле разбили на два участка. Площадь первого участка а га, а второго b га. С каждого гектара первого участка собрали 32 ц пшеницы, а с каждого гектара второго участка собрали 40 ц пшеницы. Сколько пшеницы собрали с обоих участков? Вычислите при а = 120, b = 80.

S₂ = b га, собрали по 40 ц с каждого га

32 ∙ 120 + 40 ∙ 80 = 3840 + 3200 = 7040 (ц).Ответ: 7040 ц.

Источник

2. Выражения с переменными

Двигаясь со скоростью 60 км/ч, автомобиль за 2 ч пройдёт 60 • 2 км, за 3 ч — 60 • 3 км, за 5 ч — 60-5 км, за 5,5 ч — 60 • 5,5 км. Вообще за t ч он пройдёт 60t км. Изменяя значение t, мы можем с помощью выражения 60t находить путь, пройденный автомобилем за разные промежутки времени. Для этого достаточно вместо буквы t подставить её значение и выполнить умножение. Букву t в выражении 60t называют переменной, а само выражение 60t — виражением с переменной.

Если в выражение с переменными подставить вместо каждой переменной какое-либо её значение, то получится числовое выражение. Его значение называют значением вы ражения с переменными при выбранных значениях переменных.

Так, число 88 есть значение выражения ab при a = 8 и b = 11, число 100 есть значение этого выражения при а = 25 и b = 4.

Рассмотрим выражение . При любом b ≠ 3 можно найти его значение. Например, если b = 13, то .

Некоторые выражения имеют смысл нри всех значениях переменных. Примерами могут служить выражения

Выражения с переменными используются для записи формул.

Любое чётное число m можно представить в виде произведения числа 2 и целого числа n, т. е.

Если в эту формулу вместо n подставлять целые числа, то значениями переменной m будут чётные числа. Формулу m = 2n называют формулой чётного числа.

Формулу m = 2n + 1, где n — целое число, называют формулой нечётного числа.

Аналогично формуле чётного числа можно записать формулу числа, кратного любому другому натуральному числу.

Например, формулу числа, кратного 3, можно записать так: m = Зn, где n — целое число.

а) кратного 5; б) кратного 10; в) кратного 101.

а) 3% этого числа равны 1,8;

б) 85% этого числа равны 17;

в) 130% этого числа равны 3,9;

Источник

Конспект урока по алгебре на тему «Выражения с переменными» (7 класс)

урока алгебры, 7 класс

Тема : Выражения с переменными.

Цель : обеспечение усвоения учащимися понятия «выражение с переменными»

проверить знания учащихся по теме “Числовые выражения”,

ввести понятия «выражение с переменной», «числовое значение выражения с переменной», « допустимые значения переменной»;

формировать умение находить значение выражения с переменной;

развивать умение анализировать и систематизировать знания;

формировать умение высказывать и аргументировать свою точку зрения, вступать в учебное сотрудничество с учителем и одноклассниками.

Личностные : способность к самооценке на основе критерия успешности учебной деятельности.

Регулятивные : умения определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. Планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение.

Коммуникативные : умения оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.

Познавательные : умения ориентироваться в своей системе знаний, отличать новое от уже известного с помощью учителя; добывать новые знания; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

определение понятия «выражение с переменной»,

определение понятия «числовое значение выражения с переменной»,

определение понятия «допустимые значения переменных»

выявлять выражение с переменной;

выполнять в выражениях с переменной числовые подстановки и производить соответствующие вычисления;

находить допустимые значения переменных;

находить значение выражения с переменной, используя табличную форму записи.

развитие алгоритмического мышления;

овладение навыками дедуктивных и индуктивных рассуждений

Тип урока : открытие новых знаний и умений.

Формы работы учащихся : фронтальная, индивидуальная, групповая.

Методы обучения : объяснительно-иллюстративный; по внешним признакам деятельности – беседа, демонстрация, упражнения; по источнику получения: словесные, наглядные, практические.

Необходимое техническое оборудование : компьютер, мультимедийный проек­тор, интерактивная доска.

Дидактические средства : собственная презентация, фрагмент видеоурока, учебник, карточки с заданиями, маршрутный лист.

Структура и ход урока :

подготовить обучающихся к работе на урок

Приветствует учеников, задаёт вопросы об эмоциональном настрое перед началом урока. Определяет готовность ребят к уроку, выясняет количество отсутствующих, организует внимание.

Определяют свою готовность к уроку и настроение перед его началом

Коммуникат: уважительное отношение ко сверстникам, учителю.

Личностные: формирование навыков самоорганизации.

Регулятивные: контроль и оценка собственной готовности к деятельности на уроке

Проверка домашнего задания

Дидакт.задача: установить правильность и осознанность выполнения дом.задания, устранить в ходе проверки пробелы

-Откройте тетради с домашней работой, какое задание вызвало затруднение?

Предлагает примеры №5 и №7 проверить самостоятельно (ответы в маршрутных листах), а задачу №15 объяснить ученику у доски

Проверяют примеры, слушают задачу.

умение слушать собеседника.

Личностные: формирование навыков самоорганизации.

Регулятивные: контроль и оценка процесса результата действий

Дидакт.задача:проверить знания обучающихся

Организует устную работу, предлагает ответить на вопросы с целью актуализации знаний

-Что изучали на предыдущем уроке?

-Что называется числовым выражением?

-Что называется значением числового выражения?

-Когда числовое выражение не имеет смысла?

Отвечают на вопросы учителя.

-Выражение, содержащее числа, знаки действий, скобки

-Число, которое получается в результате выполнения действий.

-Если в выражении встречается деление на нуль.

Познавательные: структуирование знаний.

Коммуникативные: умение слушать собеседника, аргументировать свое мнение.

Личностные: нравственно-этического оценивания усваимого усваимого материала

Мотивация и целеполагание

Дидакт.задача:организовать и направить на постановку и достижение цели и задач учебной деятельности обучающихся

Предлагает выполнить устный счет (слайд 1)

-Почему не можем найти значение последнего выражения?

-Как в 6 классе мы называли такие выражения?

-Такие выражения будем называть выражения с переменными.

Предлагает самостоятельно сформулировать тему и цель урока.

-Откройте тетради, запишите дату, «классная работа» и тему нашего урока (запись на доске)

Выполняют устный счет

4)-20; 5)0; 6)2,9; 7)340; 8)450;

Последнее выражение вызывает затруднение

-Это не числовое выражение.

Формулируют тему и цель урока.

Выполняют записи в тетради.

Познавательные: действия постановки и решения проблем, развитие умения формулировать тему, цель и задачи урока

Коммуникативные: умение слушать собеседника, аргументировать свое мнение.

Регулятивные: выработка у обучающегося внутренней готовности к учебной деятельности.

Личностные: действия смыслообразования

Усвоение новых знаний

Дидакт.задача: дать обучающимся конкретное представление об изучаемых фактах, основной идее изучаемого материала; добиться от обучающихся восприятия, осознания, первичного обобщения и систематизации новых знаний, усвоения обучающимися способов, путей, средств получения знаний, оперирование ими.

Организует работу по открытию новых знаний.

1.Демонстрирует видеоролик «Выражения с переменными». Предлагает провести аналогию с числовыми выражениями, чтобы обучащиеся самостоятельно сформулировали определение «выражение с переменными»

Демонстрирует слайд 2, 3

2.Предлагает подготовленному ученику 1 объяснить у доски как находить значение выражения с переменными

3. Предлагает подготовленному ученику 2 объяснить понятие допустимые значения переменных.

Источник