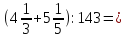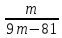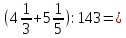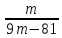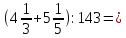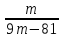Что такое выражение с переменными 7 класс алгебра мерзляк

Числовые выражения 1 урок Алгебра 7 класс Мерзляк ФГОС

Разработка адресована учителям, работающим по учебнику «Алгебра. 7 класс» авторов А.Г. Мерзляка, В.Б. Полонского, М.С. Якира.

Просмотр содержимого документа
«Числовые выражения 1 урок Алгебра 7 класс Мерзляк ФГОС»

§ 1. ВВЕДЕНИЕ В АЛГЕБРУ

Технологическая карта урока № 1

Тема урока Введение в алгебру

Тип урока Урок изучения нового материала

Предметные: познакомить учащихся с числовыми выражениями, с выражениями с переменными, алгебраическими выражениями, целыми выражениями, закрепить навыки вычисления значений числовых выражений.

Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.

Метапредметные: формировать умение использовать приобретённые знания в практической деятельности.

Учащийся научится вычислять значение числового выражения, находить значение выражения с переменными при заданных значениях переменной.

Буквенное выражение, числовое выражение, значение числового выражения, переменная, выражение с переменными, значение переменной, значение выражения с переменными, алгебраическое выражение, целое выражение.

1. Организационный момент

Как Ваше настроение?

Настроены ли Вы на работу?

Все ли принадлежности приготовлены к уроку?

Тогда в добрый путь!

Улыбнемся друг другу!

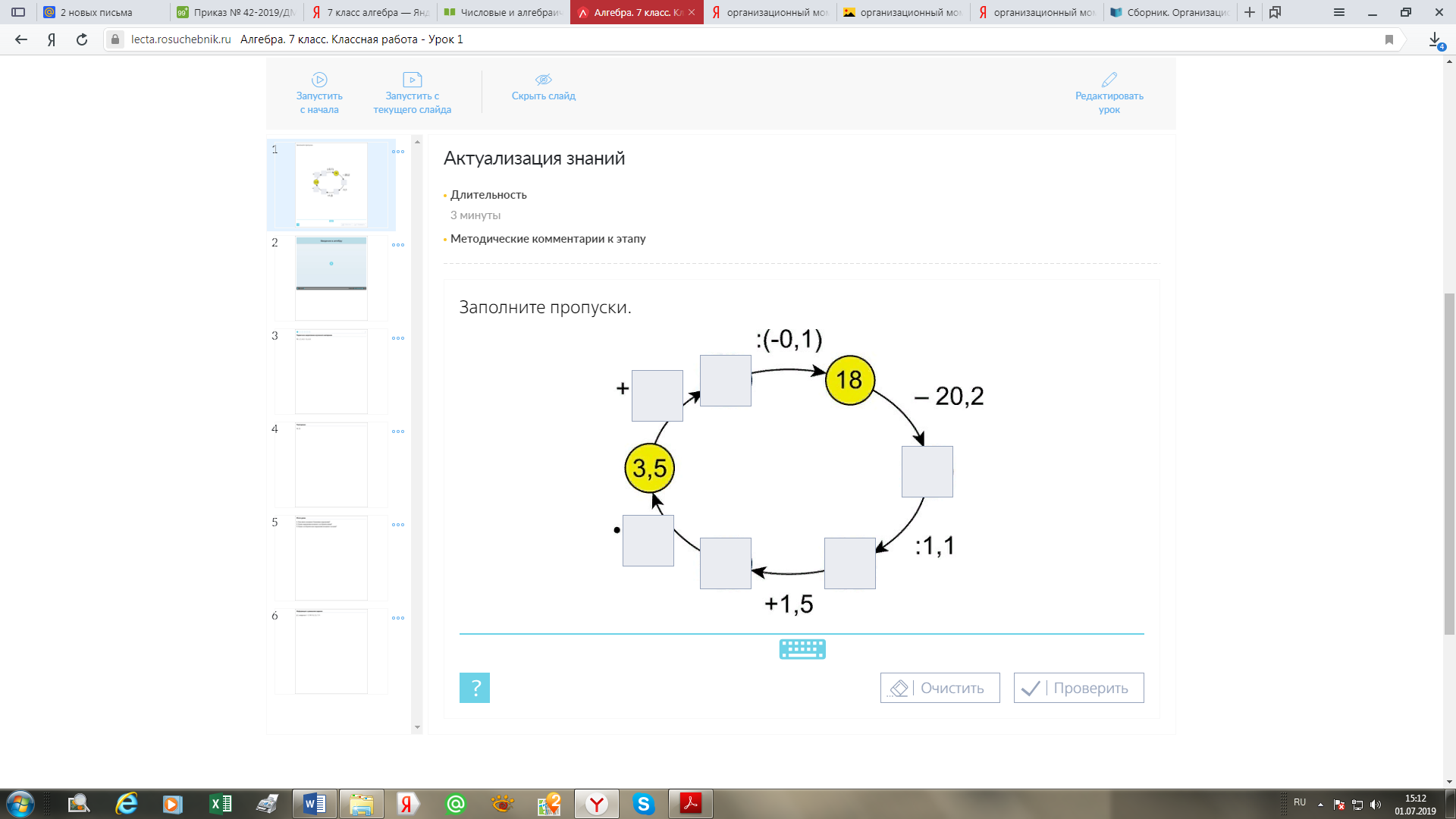
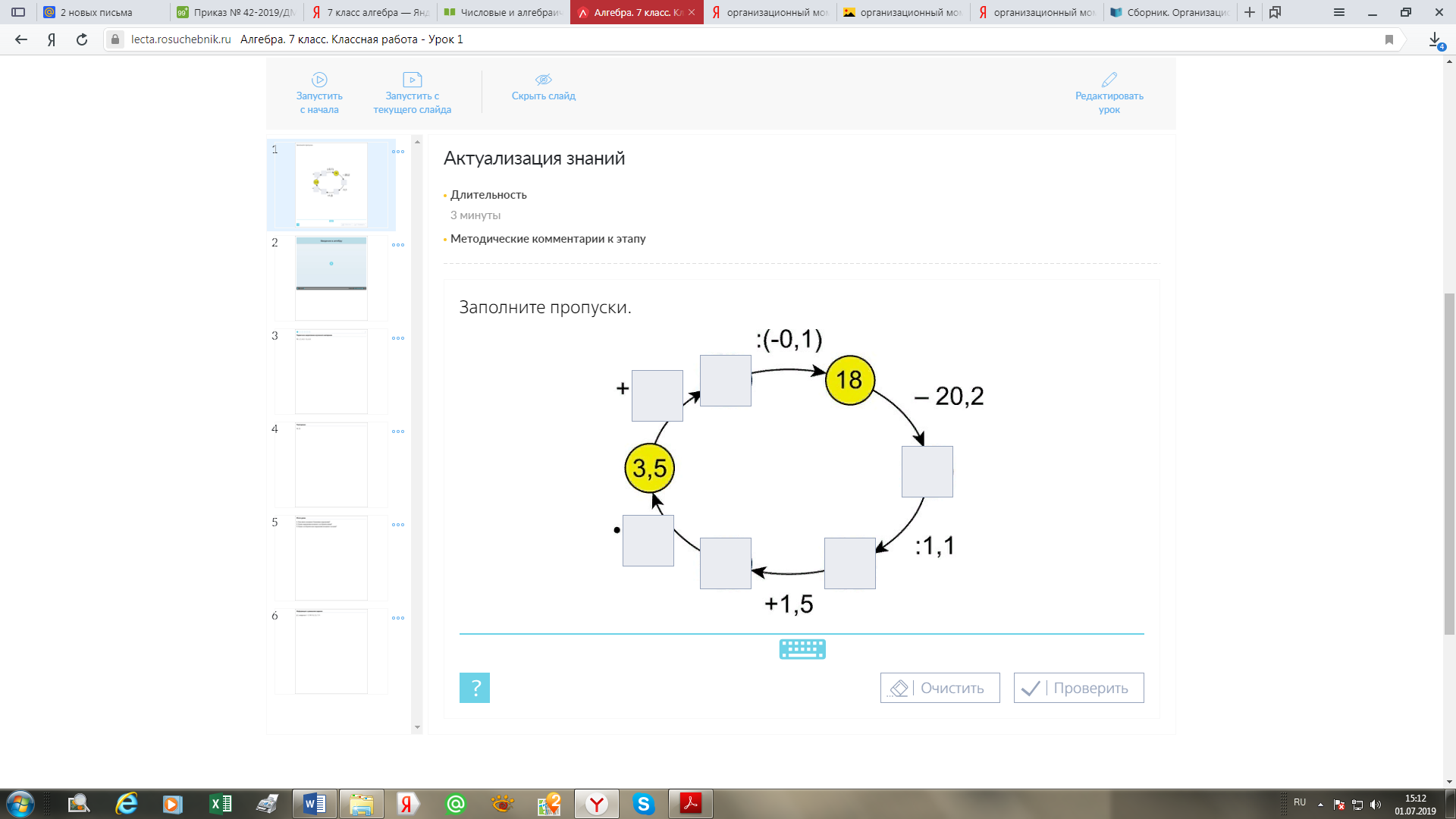
1.1.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся

Дорогие ребята! Мы с Вами уже не первый год занимаемся изучением такой нужной, сложной, и одновременно интересной науки «математики». За это время мы многое узнали, многому научились. Давайте вспомним хотя бы толику тех знаний, которые мы с Вами получили.

Придя в начальную школу, о каких числах вы узнали в первую очередь?

Какие операции над ними Вы научились выполнять?

(Это натуральные числа, числа, применяемые при счете предметов. Мы умеем складывать, вычитать, умножать и делить натуральные числа.)

В курсе математики 5-6 класса мы познакомились с десятичными и обыкновенными дробями, целыми и рациональными числами. И так же научились выполнять над ними арифметические операции.

Можно было бы человеку обойтись без этих чисел? Для чего они нам нужны?

И кажется что этого багажа знаний вполне достаточно для повседневной жизни. Однако мы пришли в 7 класс и продолжаем заниматься математикой. Правда теперь наш учебник называется «Алгеброй».

Тема нашего сегодняшнего урока: Числовые выражения

Цели: Выявление уровня вычислительных умений и навыков с рациональными числами. Повторить правила сложения, умножения, деления десятичных и обыкновенных дробей, правила действий с отрицательными и положительными числами. Углубление и систематизация сведений о числовых выражениях. Формирование умения находить значение числового выражения.

3. Изучение нового материала

(Методические комментарии к этапу

В курсе математики 5 класса учащиеся познакомились с буквенными выражениями и в дальнейшем многократно встречались с этим понятием.

Следует подчеркнуть, что обозначение чисел буквами, конструирование буквенных выражений и их преобразование, работа с формулами были первыми шагами в науку «Алгебра». Хотя этот параграф и насыщен терминами, но многие из них знакомы учащимся: числовое выражение, значение числового выражения, буквенное выражение, переменная, значение переменной, значение выражения при заданном значении переменной.

Следует заметить, что в 5 и 6 классах понятие «переменной» не вводилось, вместо него использовался термин «буква» в буквенном выражении. Поэтому, возможно, следует обратить внимание учащихся на то, что термин «выражение с переменными» означает то же, что и «буквенное выражение».

Также можно провести аналогию между буквами (переменными) в алгебраических выражениях и переменными в записи алгоритмов, с которыми учащиеся могли ознакомиться в ходе изучения курса информатики.

В параграфе не рассматривается формальное определение буквенного выражения. Однако из текста ясно, как конструируется буквенное выражение.

Схема, изображённая на с. 5 учебника, помогает лучше усвоить понятие алгебраического выражения. Разделяя алгебраические выражения на две группы — целые и дробные — мы таким образом выделяем объект, который будет изучаться в курсе алгебры 7 класса.

Отметим, что поскольку дробные выражения в этом курсе не рассматриваются, то соответствующий термин здесь не вводится.)

Теоретический материал § 1

Числовое выражение – это такое выражение, которое составлено из чисел, знаков математических действий и скобок.

3+5⋅(7−4) — числовое выражение;

3+:−5 — не числовое выражение, а бессмысленный набор символов.

Очень часто вместо конкретных чисел употребляются буквы, тогда получается алгебраическое выражение.

Алгебраическим выражением называется запись из букв, знаков арифметических действий, чисел и скобок, составленная со смыслом.

a 2 −3b — алгебраическое выражение.

Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т. е. можно менять значения букв), эти буквы называют переменными.

Алгебраические выражения могут быть очень громоздкими, и алгебра учит их упрощать, используя правила, законы, свойства, формулы.

При упрощении вычислений часто используются законы сложения и умножения.

В результате упрощений числового выражения получается число, которое называют значением числового выражения.

Выполнив указанные действия в первом примере, получим

Число 18 в ответе есть значение данного числового выражения.

О значении алгебраического выражения можно говорить только при конкретных значениях входящих в него букв.

А на ноль делить нельзя!

если при конкретных значениях букв алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми;

если же при конкретных значениях букв алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.

Так, в примере a2−3/a+2 значение a=−4 — допустимое, а

значение a=−2 — недопустимое, т. к. при нём будет деление на ноль, а делить на ноль нельзя!

4. Первичное закрепление нового материала.

Учебник № 1, 2, 4 (1–3), 6, 8

Дидактический материал № 1 (1–3), 2 (1–3), 3 (1–3)

Рабочая тетрадь №3,4

4.1. Найди значение выражения −8,9−8,1

Найди значение выражения −9,2−(−7,2).

4.2. Прочитай выражение и найди его значение.

В данном числовом выражении 2+(−4,3) записана

Прочитай выражение и найди его значение.

В данном числовом выражении 4,3÷(−2) записано

4.4. Найди значение выражения (ответ округлите до тысячных):

4.5. Выполни действия: 379,78⋅51−23,746:3,83=

4.6. Найди значение выражения: (14,35−1,75):1,4+4,7=

4.7. Выполни действия: (дробь не сокращай) 12−8=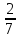

4.8. Выполни действие: −2,8−12=

4.9. Определи значение выражения:

4.10. Найди значение выражения наиболее рациональным способом:

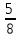
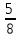
42,9⋅ −2,9⋅ =

4.11. Вычисли значение алгебраического выражения ,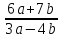

4.12. При каких значениях переменной имеет смысл выражение

4.13. Имеет ли смысл данная дробь? Если имеет смысл то найти ее значение. =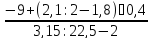

4.14. В выражении 8⋅12+18:3−2 расставь скобки так, чтобы его значение было наибольшим.

1. Как иначе называют буквенные выражения?

2. Какие выражения называют алгебраическими?

3. Какие алгебраические выражения называют целыми?

Источник

ГДЗ по Алгебре 7 класс: Мерзляк А.Г.

Издание: Алгебра. 7 класс. Учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Вентана-Граф. 2015-2018г.

Структура решебника

Номера

Решебник по алгебре для 7 класса Мерзляк – это сборник онлайн-решений по упражнениям одноименного учебника математики, составленного авторитетными российскими учеными – Мерзляком А.Г., Полонским В.Б., Якиром М.С. в 2015 году, который ныне включен в учебную программу многих российских общеобразовательных школ.

Онлайн-решебник к алгебре 7 класс Мерзляка – спутник идеальной домашней работы

Для того чтобы успевать по предметам школьной программы, качественно выполнять задания на контрольных и экзаменах семиклассникам крайне важно уметь управлять своим временем. В этом вопросе им поможет решебник по алгебре за 7 класс Мерзляк сайта ГДЗ Путина, который позволяет находить ответы и решения в один клик.

Как работает система? Решебник можно найти по названию или фамилии автора через поиск, в таблице выбрать и кликнуть номер упражнения и получить готовый ответ.

В чем главные преимущества ресурса ГДЗ Путина?

Благодаря онлайн-решебникам школьник может дома разобраться с решением сложных задач без помощи репетиторов и посещения дополнительных занятий.

ГДЗ по алгебре для 7 класса по Мерзляку – практическое дополнение дисциплины

В седьмом классе школьники переходят на новый этап постижения математики – начинаются основы алгебры и анализа. Они предусматривают не только доскональное знание формул сокращенного умножения, декартовой системы координат, синусов и косинусов, но также умение их применять на практике.

При таком раскладе – использование ГДЗ по алгебре за 7 класс Мерзляка – объективная необходимость, которая позволяет глубоко понимать предмет, качественно решать примеры и задачки. Какие задачи и примеры содержит решебник?

Сборник онлайн-решений составлен на основе учебник Мерзляка А.Г. по алгебре, изданного в 2015 году. Он выступает важной составляющей в подготовке школьников к экзаменам и контрольным.

Источник

Первый урок Алгебра 7 класс Мерзляк. Буквенные и числовые вырабения.

Разработка адресована учителям, работающим по учебнику «Алгебра. 7 класс» авторов А.Г. Мерзляка, В.Б. Полонского, М.С. Якира.

Содержимое разработки

§ 1. ВВЕДЕНИЕ В АЛГЕБРУ

Технологическая карта урока № 1

Тема урока Введение в алгебру

Тип урока Урок изучения нового материала

Предметные: познакомить учащихся с числовыми выражениями, с выражениями с переменными, алгебраическими выражениями, целыми выражениями, закрепить навыки вычисления значений числовых выражений.

Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.

Метапредметные: формировать умение использовать приобретённые знания в практической деятельности.

Учащийся научится вычислять значение числового выражения, находить значение выражения с переменными при заданных значениях переменной.

Буквенное выражение, числовое выражение, значение числового выражения, переменная, выражение с переменными, значение переменной, значение выражения с переменными, алгебраическое выражение, целое выражение.

1. Организационный момент

Как Ваше настроение?

Настроены ли Вы на работу?

Все ли принадлежности приготовлены к уроку?

Тогда в добрый путь!

Улыбнемся друг другу!

1.1.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся

Дорогие ребята! Мы с Вами уже не первый год занимаемся изучением такой нужной, сложной, и одновременно интересной науки «математики». За это время мы многое узнали, многому научились. Давайте вспомним хотя бы толику тех знаний, которые мы с Вами получили.

Придя в начальную школу, о каких числах вы узнали в первую очередь?

Какие операции над ними Вы научились выполнять?

(Это натуральные числа, числа, применяемые при счете предметов. Мы умеем складывать, вычитать, умножать и делить натуральные числа.)

В курсе математики 5-6 класса мы познакомились с десятичными и обыкновенными дробями, целыми и рациональными числами. И так же научились выполнять над ними арифметические операции.

Можно было бы человеку обойтись без этих чисел? Для чего они нам нужны?

И кажется что этого багажа знаний вполне достаточно для повседневной жизни. Однако мы пришли в 7 класс и продолжаем заниматься математикой. Правда теперь наш учебник называется «Алгеброй».

Тема нашего сегодняшнего урока: Числовые выражения

Цели: Выявление уровня вычислительных умений и навыков с рациональными числами. Повторить правила сложения, умножения, деления десятичных и обыкновенных дробей, правила действий с отрицательными и положительными числами. Углубление и систематизация сведений о числовых выражениях. Формирование умения находить значение числового выражения.

3. Изучение нового материала

(Методические комментарии к этапу

В курсе математики 5 класса учащиеся познакомились с буквенными выражениями и в дальнейшем многократно встречались с этим понятием.

Следует подчеркнуть, что обозначение чисел буквами, конструирование буквенных выражений и их преобразование, работа с формулами были первыми шагами в науку «Алгебра». Хотя этот параграф и насыщен терминами, но многие из них знакомы учащимся: числовое выражение, значение числового выражения, буквенное выражение, переменная, значение переменной, значение выражения при заданном значении переменной.

Следует заметить, что в 5 и 6 классах понятие «переменной» не вводилось, вместо него использовался термин «буква» в буквенном выражении. Поэтому, возможно, следует обратить внимание учащихся на то, что термин «выражение с переменными» означает то же, что и «буквенное выражение».

Также можно провести аналогию между буквами (переменными) в алгебраических выражениях и переменными в записи алгоритмов, с которыми учащиеся могли ознакомиться в ходе изучения курса информатики.

В параграфе не рассматривается формальное определение буквенного выражения. Однако из текста ясно, как конструируется буквенное выражение.

Схема, изображённая на с. 5 учебника, помогает лучше усвоить понятие алгебраического выражения. Разделяя алгебраические выражения на две группы — целые и дробные — мы таким образом выделяем объект, который будет изучаться в курсе алгебры 7 класса.

Отметим, что поскольку дробные выражения в этом курсе не рассматриваются, то соответствующий термин здесь не вводится.)

Теоретический материал § 1

Числовое выражение – это такое выражение, которое составлено из чисел, знаков математических действий и скобок.

3+5⋅(7−4) — числовое выражение;

3+:−5 — не числовое выражение, а бессмысленный набор символов.

Очень часто вместо конкретных чисел употребляются буквы, тогда получается алгебраическое выражение.

Алгебраическим выражением называется запись из букв, знаков арифметических действий, чисел и скобок, составленная со смыслом.

a 2 −3b — алгебраическое выражение.

Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т. е. можно менять значения букв), эти буквы называют переменными.

Алгебраические выражения могут быть очень громоздкими, и алгебра учит их упрощать, используя правила, законы, свойства, формулы.

При упрощении вычислений часто используются законы сложения и умножения.

В результате упрощений числового выражения получается число, которое называют значением числового выражения.

Выполнив указанные действия в первом примере, получим

Число 18 в ответе есть значение данного числового выражения.

О значении алгебраического выражения можно говорить только при конкретных значениях входящих в него букв.

А на ноль делить нельзя!

если при конкретных значениях букв алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми;

если же при конкретных значениях букв алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.

Так, в примере a2−3/a+2 значение a=−4 — допустимое, а

значение a=−2 — недопустимое, т. к. при нём будет деление на ноль, а делить на ноль нельзя!

4. Первичное закрепление нового материала.

Учебник № 1, 2, 4 (1–3), 6, 8

Дидактический материал № 1 (1–3), 2 (1–3), 3 (1–3)

Рабочая тетрадь №3,4

4.1. Найди значение выражения −8,9−8,1

Найди значение выражения −9,2−(−7,2).

4.2. Прочитай выражение и найди его значение.

В данном числовом выражении 2+(−4,3) записана

Прочитай выражение и найди его значение.

В данном числовом выражении 4,3÷(−2) записано

4.4. Найди значение выражения (ответ округлите до тысячных):

4.5. Выполни действия: 379,78⋅51−23,746:3,83=

4.6. Найди значение выражения: (14,35−1,75):1,4+4,7=

4.7. Выполни действия: (дробь не сокращай) 12−8=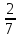

4.8. Выполни действие: −2,8−12=

4.9. Определи значение выражения:

4.10. Найди значение выражения наиболее рациональным способом:

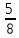
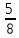
42,9⋅ −2,9⋅ =

4.11. Вычисли значение алгебраического выражения ,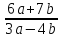

4.12. При каких значениях переменной имеет смысл выражение

4.13. Имеет ли смысл данная дробь? Если имеет смысл то найти ее значение. =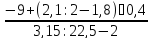

4.14. В выражении 8⋅12+18:3−2 расставь скобки так, чтобы его значение было наибольшим.

1. Как иначе называют буквенные выражения?

2. Какие выражения называют алгебраическими?

3. Какие алгебраические выражения называют целыми?

Источник

Числовые выражения 1 урок Алгебра 7 класс Мерзляк ФГОС

Разработка адресована учителям, работающим по учебнику «Алгебра. 7 класс» авторов А.Г. Мерзляка, В.Б. Полонского, М.С. Якира.

Содержимое разработки

§ 1. ВВЕДЕНИЕ В АЛГЕБРУ

Технологическая карта урока № 1

Тема урока Введение в алгебру

Тип урока Урок изучения нового материала

Предметные: познакомить учащихся с числовыми выражениями, с выражениями с переменными, алгебраическими выражениями, целыми выражениями, закрепить навыки вычисления значений числовых выражений.

Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.

Метапредметные: формировать умение использовать приобретённые знания в практической деятельности.

Учащийся научится вычислять значение числового выражения, находить значение выражения с переменными при заданных значениях переменной.

Буквенное выражение, числовое выражение, значение числового выражения, переменная, выражение с переменными, значение переменной, значение выражения с переменными, алгебраическое выражение, целое выражение.

1. Организационный момент

Как Ваше настроение?

Настроены ли Вы на работу?

Все ли принадлежности приготовлены к уроку?

Тогда в добрый путь!

Улыбнемся друг другу!

1.1.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся

Дорогие ребята! Мы с Вами уже не первый год занимаемся изучением такой нужной, сложной, и одновременно интересной науки «математики». За это время мы многое узнали, многому научились. Давайте вспомним хотя бы толику тех знаний, которые мы с Вами получили.

Придя в начальную школу, о каких числах вы узнали в первую очередь?

Какие операции над ними Вы научились выполнять?

(Это натуральные числа, числа, применяемые при счете предметов. Мы умеем складывать, вычитать, умножать и делить натуральные числа.)

В курсе математики 5-6 класса мы познакомились с десятичными и обыкновенными дробями, целыми и рациональными числами. И так же научились выполнять над ними арифметические операции.

Можно было бы человеку обойтись без этих чисел? Для чего они нам нужны?

И кажется что этого багажа знаний вполне достаточно для повседневной жизни. Однако мы пришли в 7 класс и продолжаем заниматься математикой. Правда теперь наш учебник называется «Алгеброй».

Тема нашего сегодняшнего урока: Числовые выражения

Цели: Выявление уровня вычислительных умений и навыков с рациональными числами. Повторить правила сложения, умножения, деления десятичных и обыкновенных дробей, правила действий с отрицательными и положительными числами. Углубление и систематизация сведений о числовых выражениях. Формирование умения находить значение числового выражения.

3. Изучение нового материала

(Методические комментарии к этапу

В курсе математики 5 класса учащиеся познакомились с буквенными выражениями и в дальнейшем многократно встречались с этим понятием.

Следует подчеркнуть, что обозначение чисел буквами, конструирование буквенных выражений и их преобразование, работа с формулами были первыми шагами в науку «Алгебра». Хотя этот параграф и насыщен терминами, но многие из них знакомы учащимся: числовое выражение, значение числового выражения, буквенное выражение, переменная, значение переменной, значение выражения при заданном значении переменной.

Следует заметить, что в 5 и 6 классах понятие «переменной» не вводилось, вместо него использовался термин «буква» в буквенном выражении. Поэтому, возможно, следует обратить внимание учащихся на то, что термин «выражение с переменными» означает то же, что и «буквенное выражение».

Также можно провести аналогию между буквами (переменными) в алгебраических выражениях и переменными в записи алгоритмов, с которыми учащиеся могли ознакомиться в ходе изучения курса информатики.

В параграфе не рассматривается формальное определение буквенного выражения. Однако из текста ясно, как конструируется буквенное выражение.

Схема, изображённая на с. 5 учебника, помогает лучше усвоить понятие алгебраического выражения. Разделяя алгебраические выражения на две группы — целые и дробные — мы таким образом выделяем объект, который будет изучаться в курсе алгебры 7 класса.

Отметим, что поскольку дробные выражения в этом курсе не рассматриваются, то соответствующий термин здесь не вводится.)

Теоретический материал § 1

Числовое выражение – это такое выражение, которое составлено из чисел, знаков математических действий и скобок.

3+5⋅(7−4) — числовое выражение;

3+:−5 — не числовое выражение, а бессмысленный набор символов.

Очень часто вместо конкретных чисел употребляются буквы, тогда получается алгебраическое выражение.

Алгебраическим выражением называется запись из букв, знаков арифметических действий, чисел и скобок, составленная со смыслом.

a 2 −3b — алгебраическое выражение.

Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т. е. можно менять значения букв), эти буквы называют переменными.

Алгебраические выражения могут быть очень громоздкими, и алгебра учит их упрощать, используя правила, законы, свойства, формулы.

При упрощении вычислений часто используются законы сложения и умножения.

В результате упрощений числового выражения получается число, которое называют значением числового выражения.

Выполнив указанные действия в первом примере, получим

Число 18 в ответе есть значение данного числового выражения.

О значении алгебраического выражения можно говорить только при конкретных значениях входящих в него букв.

А на ноль делить нельзя!

если при конкретных значениях букв алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми;

если же при конкретных значениях букв алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.

Так, в примере a2−3/a+2 значение a=−4 — допустимое, а

значение a=−2 — недопустимое, т. к. при нём будет деление на ноль, а делить на ноль нельзя!

4. Первичное закрепление нового материала.

Учебник № 1, 2, 4 (1–3), 6, 8

Дидактический материал № 1 (1–3), 2 (1–3), 3 (1–3)

Рабочая тетрадь №3,4

4.1. Найди значение выражения −8,9−8,1

Найди значение выражения −9,2−(−7,2).

4.2. Прочитай выражение и найди его значение.

В данном числовом выражении 2+(−4,3) записана

Прочитай выражение и найди его значение.

В данном числовом выражении 4,3÷(−2) записано

4.4. Найди значение выражения (ответ округлите до тысячных):

4.5. Выполни действия: 379,78⋅51−23,746:3,83=

4.6. Найди значение выражения: (14,35−1,75):1,4+4,7=

4.7. Выполни действия: (дробь не сокращай) 12−8=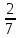

4.8. Выполни действие: −2,8−12=

4.9. Определи значение выражения:

4.10. Найди значение выражения наиболее рациональным способом:

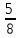
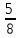
42,9⋅ −2,9⋅ =

4.11. Вычисли значение алгебраического выражения ,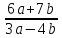

4.12. При каких значениях переменной имеет смысл выражение

4.13. Имеет ли смысл данная дробь? Если имеет смысл то найти ее значение. =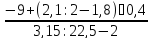

4.14. В выражении 8⋅12+18:3−2 расставь скобки так, чтобы его значение было наибольшим.

1. Как иначе называют буквенные выражения?

2. Какие выражения называют алгебраическими?

3. Какие алгебраические выражения называют целыми?

Источник