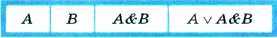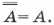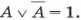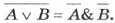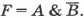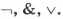Что такое высказывание в информатике приведите пример
Презентация к уроку
ПРОДОЛЖИТЕЛЬНОСТЬ УРОКА: 40 минут.
I. Организационный момент.
Приветствие, отметка отсутствующих на уроке.
Продолжаем изучать раздел «Логический язык». Сегодня наше занятие посвящено теме «Логические высказывания». Работу начнем с проверки домашнего задания (зачитываются стихотворения обучающихся, в которых содержится много логических связок (операций) и делается вывод, что произвольную информацию можно однозначно интерпретировать на основе алгебры логики).
III. Актуализация знаний (фронтальный опрос).
Итак, что же такое высказывание? (Повествовательное предложение, относительно которого можно сказать истинно оно или ложно.)
Что такое простое высказывание? (Высказывание называется простым (элементарным), если никакая его часть не является высказыванием.)
Что такое составное высказывание? (Составное высказывание состоит из простых высказываний, соединенных логическими связками (операциями).)
IV. Презентация нового материала.
Рассмотрим правило построения отрицания к простому высказыванию.
Правило: При построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что», либо отрицание строится к сказуемому, тогда к сказуемому добавляется частица «не», при этом слово «все» заменяется на «некоторые» и наоборот.
Графически отрицание можно изобразить в виде множества. (слайд 11)
Графически конъюнкцию можно изобразить в виде множества. (слайд 13)
Графически дизъюнкцию можно изобразить в виде множества. (слайд 15)
Итак, назовите три базовые операции, которые мы изучили. (слайд 16)
Давайте попробуем применить новые знания при выполнении проверочной работы.
V. Закрепление изученного материала (работа у доски).
Задание 5. Приведите в соответствие диаграмму и ее обозначение. (слайд 17)
Задание 7. Приведите в соответствие определения или обозначения. Выпишите соответствующие номера.
| 1. Логика | 1. Логическое сложение |
| 2. Высказывание | 2. Наука о формах и способах мышления |
| 3. Алгебра логики | 3. Логическое отрицание |
| 4. Дизъюнкция | 4. ИСТИНА и ЛОЖЬ |
| 5. Логическая константа | 5. Наука об операциях над высказываниями |
| 6. Инверсия | 6. Повествовательное предложение, в котором что-либо утверждается или отрицается |
| 7. Конъюнкция | 7. & |
Ответ: 1-2; 2-6; 3-5; 4-1; 5-4; 6-3; 7-7.
4) А v B
Ответы: 1) 0; 2) 1; 3) 0; 4) 1.
VII. Заключение. Домашнее задание.
Оценивается работа класса в целом и отдельных учащихся, отличившихся на уроке.
1) Выучить основные определения, знать обозначения.
2) Придумать простые высказывания. (Всего должно быть 5 наборов по два высказывания). Из них составить всевозможные составные высказывания, определить их истинность.
Что такое высказывание в информатике приведите пример
Простые и сложные высказывания, логические переменные и логические константы, логическое отрицание, логическое умножение, логическое сложение, таблицы истинности для логических операций
Для описания рассуждений и правил выполнения действий с информацией используют специальный язык, принятый в математической логике. В основе рассуждений содержатся специальные предложения, называемые высказываниями. В высказываниях всегда что-либо утверждается или отрицается об объектах, их свойствах и отношениях между объектами. Высказыванием является любое суждение, относительно которого можно сказать, истинно оно или ложно. Высказываниями могут быть только повествовательные предложения. Вопросительные или побудительные предложения высказываниями не являются.
Высказывание — суждение, сформулированное в виде повествовательного предложения, о котором можно сказать, истинно оно или ложно.
Например, вопросительные предложения «В каком году было первое летописное упоминание о Москве?» и «Что является внешней памятью компьютера?» или побудительное предложение «Соблюдайте правила техники безопасности в компьютерном классе» высказываниями не являются. Повествовательные предложения «Первое летописное упоминание о Москве было в 1812 г.», «Оперативное запоминающее устройство является внешней памятью компьютера» и «В компьютерном классе не надо соблюдать правила техники безопасности» являются высказываниями, поскольку это суждения, о каждом из которых можно сказать, что оно ложно. Истинными высказываниями будут суждения «Первое летописное упоминание о Москве было в 1147 г.», «Жесткий магнитный диск является внешней памятью компьютера».
Каждому высказыванию соответствует только одно из двух значений: или «истина», или «ложь», которые являются логическими константами. Истинное значение принято обозначать цифрой 1, а ложное значение — цифрой 0. Высказывания можно обозначать с помощью логических переменных, в качестве которых используются заглавные латинские буквы. Логические переменные могут принимать только одно из двух возможных значений: «истина» или «ложь». Например, высказывание «Информация в компьютере кодируется с помощью двух знаков» можно обозначить логической переменной А, а высказывание «Принтер является устройством хранения информации» можно обозначить логической переменной В. Поскольку первое высказывание соответствует действительности, то А = 1. Такая запись означает, что высказывание А истинно. Так как второе высказывание не соответствует действительности, то В = 0. Такая запись означает, что высказывание в ложно.
Высказывания могут быть простыми и сложными. Высказывание называется простым, если никакая его часть не является высказыванием. До сих пор были приведены примеры простых высказываний, которые обозначались логическими перемены ми. Выстраивая цепочку рассуждений, человек с помощью логических операций объединяет простые высказывания в сложнее’ высказывания. Чтобы узнать значение сложного высказывания нет необходимости вдумываться в его содержание. Достаточно знать значение простых высказываний, составляющих сложное высказывание, и правила выполнения логических операций.
Логическая операция — действие, позволяющее составлять сложное высказывание из простых высказываний.
Все рассуждения человека, а также работа современных технических устройств основываются на типовых действиях с информацией — трех логических операциях: логическом отрицании (инверсии), логическом умножении (конъюнкции) и логическом сложении (дизъюнкции).
Логическое отрицание простого высказывания получают добавлением слов «Неверно, что» в начале простого высказывания.
■ ПРИМЕР 1. Имеется простое высказывание «Крокодилы умеют летать». Результатом логического отрицания будет высказывание «Неверно, что крокодилы умеют летать». Значение исходного высказывания — «ложь», а значение нового — «истина».
■ ПРИМЕР 2. Имеется простое высказывание «Файл должен иметь имя». Результатом логического отрицания будет высказывание «Неверно, что файл должен иметь имя». Значение исходного высказывания — «истина», а значение нового высказывания — «ложь».
Можно заметить, что логическое отрицание высказывания истинно, когда исходное высказывание ложно, и наоборот, логическое отрицание высказывания ложно, когда исходное высказывание истинно.
Логическое отрицание (инверсия) — логическая операция, ставящая в соответствие простому высказыванию новое высказывание, значение которого противоположно значению исходного высказывания.
Обозначим простое высказывание логической переменной А. Тогда логическое отрицание этого высказывания будем обозначать НЕ А. Запишем все возможные значения логической переменной А и соответствующие результаты логического отрицания НЕ А в виде таблицы, которая называется таблицей истинности для логического отрицания (табл. 40).
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО ОТРИЦАНИЯ
Если/1 = 0, то НЕ А = 1 (см. пример 1).
Если А = 1, то НЕ А = 0 (см. пример 2)
Можно заметить, что в таблице истинности для логического отрицания ноль меняется на единицу, а единица меняется на ноль.
Логическое умножение двух простых высказываний получают объединением этих высказываний с помощью союза и. Разберем на примерах 3—6, что будет являться результатом логического умножения.
■ ПРИМЕР 3. Имеются два простых высказывания. Одно высказывание — «Карлсон живет в подвале». Другое высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале, и Карлсон лечится мороженым». Можно сформулировать новое высказывание более кратко: «Карлсон живет в подвале и лечится мороженым». Оба исходных высказывания ложны. Значение нового сложного высказывания также «ложь».
■ ПРИМЕР 4. Имеются два простых высказывания. Первое высказывание — «Карлсон живет в подвале». Второе высказывание — «Карлсон лечится вареньем».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале и лечится вареньем». Первое исходное высказывание ложно, а второе истинно. Значение нового сложного высказывания — «ложь».
■ ПРИМЕР 5. Имеются два простых высказывания. Первое высказывание — «Карлсон живет на крыше». Второе высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится мороженым». Первое исходное высказывание истин но, а второе ложно. Значение нового сложного высказывания «ложь».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится вареньем». Оба исходных высказывания истинны. Зпачение нового сложного высказывания также «истина».
Можно заметить, что логическое умножение двух высказываний истинно только в одном случае — когда оба исходных высказывания истинн ы.
Логическое умножение (конъюнкция) — логическая операция, ставящая в соответствие двум простым высказываниям новое высказывание, значение которого истинно тогда и только тогда, когда оба исходных высказывания истинны.
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО УМНОЖЕНИЯ
Презентация по информатике на тему «Высказывания»
Описание презентации по отдельным слайдам:
Тема урока: «Высказывания»
Пример 1. Определить значения истинности для следующих высказываний. «Лёд – твёрдое состояние воды». «Треугольник – это геометрическая фигура». «Париж – столица Китая».
Высказывания бывают: Общие (все, всякий, каждый, ни один). Частные (некоторые, большинство и т. п.). Единичные.
Пример 2. Определить тип высказывания. «Все рыбы умеют плавать». «Некоторые медведи – бурые». «Буква А – гласная».
Высказывания делятся на: Простые. Составные.
«Процессор является устройством обработки информации, и принтер является устройством печати»
А = «Два умножить на два равно четырем». В = «Два умножить на два равно пяти». А = 1 В = 0
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0)
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Современные педтехнологии в деятельности учителя
Курс профессиональной переподготовки
Информатика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Презентация состоит из 9 слайдов. К слайдам применена анимация. Презентацию можно использовать, как для работы на аудиторию, так и для индивидуальной работы. В начале даётся определение понятия «Высказывание (суждение)» и делается заключение о истинности или ложности любого высказывания.Далее на примерах рассматривается истинность и ложность данных высказываний. Следующий слайд знакомит с типами высказываний (общие, частные, единичные). А далее эти понятия закрепляются на примерах. Последующий слайд знакомит с простыми и сложными высказываниями и эти два понятия закрепляются на примерах. И, наконец последний слайд знакомит с обозначением высказываний.
Номер материала: 293636
Не нашли то что искали?
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Онлайн-конференция о профориентации и перспективах рынка труда
Время чтения: 3 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Рособрнадзор объявил сроки и формат ЕГЭ
Время чтения: 1 минута
Путин призвал повышать уровень общей подготовки в колледжах
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Ключевые слова:
1.3.1. Высказывание

Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.

Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six Is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.

Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.
Относительно предложения «Компьютерная графика — самая интересная тема в курсе школьной информатики» также нельзя однозначно сказать, истинно оно или ложно. Подумайте сами почему.

Например, не являются высказываниями такие предложения, как: «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл?».

Построим таблицу истинности для логического выражения A ∨ А & В. В нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:
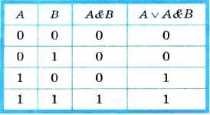
Наборы входных переменных — это целые числа от О до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11. Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение A ∨ А & Б равносильно логическому выражению А.
1.3.4. Свойства логических операций
Рассмотрим основные свойства (законы) алгебры логики.
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
A ∨ (B & С) = (A ∨ В) & (A ∨ С).
Законы алгебры логики могут быть доказаны с помощью таблиц истинности.
Докажем распределительный закон для логическического сложения:
A ∨ (В & С) = (А ∨ В) & (A ∨ С).
Совпадение столбцов, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Пример 2. Найдём значение логического выражения 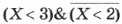
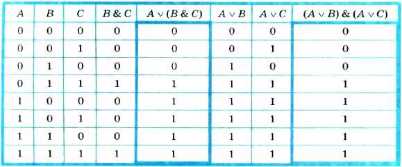
1 С учётом того, что ваза разбита одним внуком, можно было составлять не всю таблицу, а только её фрагмент, содержащий следуюнще наборы входных переменных: 001, 010, 100.
Исходя из того, что знает о внуках бабушка, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10). Таких строк в таблице оказалось две (они отмечены галочками). Согласно второй из них, вазу разбили Коля и Вася, что противоречит условию. Согласно первой из найденных строк, вазу разбил Серёжа, он же оказался хитрецом. Шутником оказался Вася. Имя правдивого внука — Коля.
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах?
Решение. Рассмотрим простые высказывания:
C1 = «Сима заняла первое место»;
В2 = «Валя заняла второе место»;
С2 = «Сима заняла второе место»;
Д3 = «Даша заняла третье место»;
А2 = «Алла заняла второе место»;
Д4 = «Даша заняла четвёртое место».
Логическое произведение истинных высказываний будет истинным:
На основании распределительного закона преобразуем левую часть этого выражения:
Высказывание С1 • С2 означает, что Сима заняла и первое, и второе места. Согласно условию задачи, это высказывание ложно. Ложным является и высказывание В2 • С2. Учитывая закон операций с константой 0, запишем:
Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных высказываний дают:
Из последнего равенства следует, что С1 = 1, Д3 = 1, А2 = 1. Это означает, что Сима заняла первое место, Алла — второе, Даша — третье. Следовательно, Валя заняла четвёртое место.
Познакомиться с другими способами решения логических задач, а также принять участие в Интернет-олимпиадах и конкурсах по их решению вы сможете на сайте «Математика для школьников» (http://www.kenqyry.com/).
На сайте http://www.kaser.com/ вы сможете скачать демонстрационную версию очень полезной, развивающей логику и умение рассуждать логической головоломки Шерлок.
1.3.6. Логические элементы
Алгебра логики — раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Вы уже знаете, что любая информация может быть представлена в дискретной форме — в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
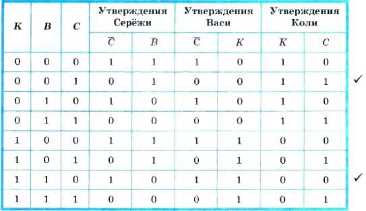
На рис. 1.5 приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.
Рис 1.5.
Логические элементы
Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 1.5, а). Единица на выходе этого элемента появится только тогда, когда на всех входах будут единицы.
Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рис. 1.5, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.
Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 1.5, в). Если на входе элемента О, то на выходе 1 и наоборот.
Компьютерные устройства, производящие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти вопросы будут раскрыты в курсе информатики 10-11 классов.
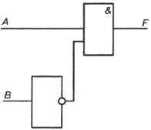
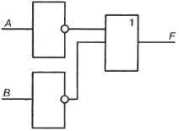
Пример 3. Проанализируем электронную схему, т. е. выясним, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах.
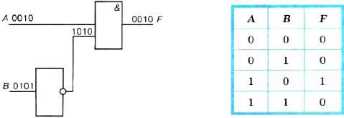
Решение. Все возможные комбинации сигналов на входах А к В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.
Таблицу истинности можно построить и по логическому выражению, соответствующему электронной схеме. Последний логический элемент в рассматриваемой схеме — конъюнктор. В него поступают сигналы от входа Л и от инвертора. В свою очередь, в инвертор поступает сигнал от входа В. Таким образом,
Составить более полное представление о логических элементах и электронных схемах вам поможет работа с тренажёром «Логика» (http://kpolyakov. narod. ru/prog/logic. htm).
Самое главное
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.
Таблицы истинности для основных логических операций:
При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций:
Вопросы и задания
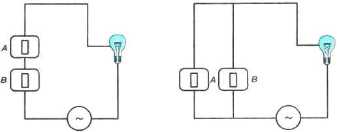
На них изображены известные вам из курса физики параллельное и последовательное соединения переключателей. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателей. Попытайтесь самостоятельно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:
По запросу сомики & гуппи было найдено 0 сайтов, по запросу сомики & меченосцы — 20 сайтов, а по запросу меченосцы & гуппи — 10 сайтов.
Сколько сайтов будет найдено по запросу сомики | меченосцы | гуппи?
Смит: «Я не делал этого. Браун сделал это».
Джон: «Браун не виновен. Смит сделал это».
Браун: «Я не делал этого. Джон не делал этого».
Электронное приложение к уроку
 |  |  |
| Файлы | Материалы урока | Ресурсы ЭОР |
Cкачать материалы урока