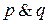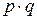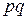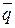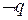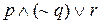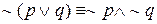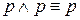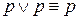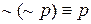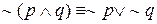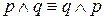Что такое высказывание в логике кратко
Высказывание (логика)
Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание. Пример: A(x) = «В городе x идёт дождь.», где A — высказывательная форма, x — объект.
Содержание
Виды высказываний
Логические высказывания принято подразделять на два вида: элементарные логические высказывания и составные логические высказывания.
Составное логическое высказывание — это высказывание, образованное из других высказываний с помощью логических связок.
Элементарные логические высказывания — это высказывания не относящиеся к составным.
Примеры: «Петров — врач», «Петров — шахматист» — элементарные логические высказывания. «Петров — врач и шахматист» — составное логическое высказывание, состоящие из двух элементарных высказываний, связанных между собой при помощи связки «и».
Связь с математической логикой
Обычная логика двухзначна, то есть приписывает высказываниям только два возможных значения: истинно оно или ложно.
Пусть 


Тождественно истинное высказывание обозначают символом 1, тождественно ложное — символом 0.
Основные операции над логическими высказываниями
Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.
Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.
Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.
Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.
Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.
Кванторное логическое высказывание с квантором всеобщности (
Кванторное логическое высказывание с квантором существования (
См. также
Примечания
Литература
Полезное
Смотреть что такое «Высказывание (логика)» в других словарях:
Высказывание — Высказывание: Высказывание (логика) предложение, которое может быть истинно или ложно. Высказывание (лингвистика) предложение в конкретной речевой ситуации. См. также Суждение … Википедия
ЛОГИКА — (от греч. logos слово, понятие, рассуждение, разум), или Формальная логика, наука о законах и операциях правильного мышления. Согласно основному принципу Л., правильность рассуждения (вывода) определяется только его логической формой, или… … Философская энциклопедия
ЛОГИКА ВЫСКАЗЫВАНИЙ — раздел логики, в котором изучаются истинностные взаимосвязи между высказываниями. В рамках данного раздела высказывания (пропозиции, предложения) рассматриваются только с т.зр. их истинности или ложности, безотносительно к их внутренней субъектно … Философская энциклопедия
логика высказываний — ЛОГИКА ВЫСКАЗЫВАНИЙ, пропозициональная логика раздел символической логики, изучающий сложные высказывания, образованные из простых, и их взаимоотношения. В отличие от логики предикатов, простые высказывания при этом выступают как… … Энциклопедия эпистемологии и философии науки
ВЫСКАЗЫВАНИЕ — грамматически правильное повествовательное предложение, взятое вместе с выражаемым им смыслом. В логике употребляется несколько понятий В., существенно различающихся между собой. Прежде всего это понятие дескриптивного, или о п и с а тельного,… … Философская энциклопедия
Логика Бэрроуза — Логика Бэрроуза Абади Нидхэма (англ. Burrows Abadi Needham logic) или BAN логика (англ. BAN logic) это формальная логическая модель для анализа знания и доверия, широко используемая при анализе протоколов… … Википедия
ЛОГИКА ПРЕДИКАТОВ — центральный раздел логики, в котором изучается субъектно предикатная структура высказывании и истинностные взаимосвязи между ними. Л.п. представляет собой содержательное расширение логики высказываний. В рамках данного раздела любое высказывание… … Философская энциклопедия
ЛОГИКА НАУЧНОГО ПОЗНАНИЯ — или Логика науки, применение идей, методов и аппарата логики в анализе научного познания. Развитие логики всегда было тесно связано с практикой теоретического мышления и прежде всего с развитием науки. Конкретные рассуждения дают логике материал … Философская энциклопедия
ЛОГИКА СИМВОЛИЧЕСКАЯ — ЛОГИКА СИМВОЛИЧЕСКАЯ математическая логика. теоретическая логика область логики, в которой логические выводы исследуются посредством логических исчислений на основе строгого символического языка. Термин “символическая логика” был, по видимому … Философская энциклопедия
ЛОГИКА НАУКИ — в спец. смысле дисциплина, применяющая понятия и технич. аппарат совр. формальной логики к анализу систем науч. знания. Термин «Л. н.» часто употребляется также для обозначения законов развития науки (логика науч. развития), правил и… … Философская энциклопедия
Логическое высказывание
Логическое высказывание
Логическое высказывание — утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: ложь (0, ложно, false) или истина (1, истинно, true). Логическое высказывание принято обозначать заглавными латинскими буквами. Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание.
Пример: A(x) = «В городе x идет дождь.» A — высказывательная форма, x — объект.
Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.
Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.
Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.
Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.
Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.
Кванторное логическое высказывание с квантором всеобщности (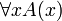
Кванторное логическое высказывание с квантором существования (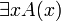
См. также
Полезное
Смотреть что такое «Логическое высказывание» в других словарях:
Высказывание (логика) — У этого термина существуют и другие значения, см. Высказывание. Высказывание термин математической логики, обозначающий формализованную структурированную запись мысли с помощью буквенных символов и логических связок, рассматриваемую с точки … Википедия
ЛОГИЧЕСКОЕ СЛЕДСТВИЕ — суждение (предложение, высказывание, формула), логически вытекающее (или, иначе, логически следующее) из посылок умозаключения (или из посылок вывода, состоящего из ряда умозаключений), т.е. выводимое из посылок на основе правил и законов логики … Философская энциклопедия
логическое следование — отношение, существующее между посылками и обоснованно выводимыми из них заключениями. Л.с. относится к числу фундаментальных, исходных понятий логики, точного универсального определения не имеет; в частности, описание его с помощью слов выводимо … Словарь терминов логики
Логическое мышление — Логика (др. греч. λογική «наука о рассуждении», «искусство рассуждения» от λόγος «речь», «рассуждение») наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это… … Википедия
логическое следствие — суждение (предложение, высказывание, формула), полученное посредством дедуктивного рассуждения из некоторых исходных суждений. * * * ЛОГИЧЕСКОЕ СЛЕДСТВИЕ ЛОГИЧЕСКОЕ СЛЕДСТВИЕ, суждение (предложение, высказывание, формула), полученное посредством… … Энциклопедический словарь
ЛОГИЧЕСКОЕ СЛЕДСТВИЕ — из данного множества посылок высказывание, являющееся истинным при любой интерпретации нелогич. символов (т. е. имен объектов, функций, предикатов), при к рой истинны посылки. Если высказывание Аявляется Л. с. из множества высказываний Г, то… … Математическая энциклопедия
Логическое следствие — суждение (предложение, высказывание, формула), логически вытекающее (или, иначе, логически следующее) из посылок умозаключения (или из посылок вывода, состоящего из ряда умозаключений), т. е. выводимое из посылок на основе правил и… … Большая советская энциклопедия
БЕСКОНЕЧНОЕ ЛОГИЧЕСКОЕ — понятие диалектической логики, введенное грузинским философом С.Б. Церетели (1907 1966). Б. Л., по определению Церетели, «есть то, отрицание чего утверждает его же. Точнее: это есть утверждение чего либо отрицанием его же». Так, говоря, что нет… … Новейший философский словарь
Логика. Краткий курс
Настоящее издание представляет собой учебное пособие, подготовленное в соответствии с Государственным образовательным стандартом по дисциплине «Логика». Материал изложен кратко, но четко и доступно, что позволит в короткие сроки успешно подготовиться и сдать экзамен или зачет по данному предмету. Издание предназначено для студентов высших учебных заведений.
Оглавление
Приведённый ознакомительный фрагмент книги Логика. Краткий курс предоставлен нашим книжным партнёром — компанией ЛитРес.
4. Классическая логика высказывании и предикатов
Под именем понимается выражение языка, обозначающее отдельный предмет, совокупность сходных предметов, свойства, отношения. Выражение языка становится именем, если оно выступает в роли подлежащего или именной части сказуемого в простом предложении: «S есть Р» (S — подлежащее, Р — сказуемое). Например, высказывание «роза — это цветок» своими составляющими имеет имена «роза» и «цветок».
Высказывание — грамматически правильное предложение, которое может быть истинным или ложным. В логике само понятие высказывания — ключевое, но не допускает универсального определения для разных ее разделов. Но любое высказывание описывает некоторую ситуацию и может быть истинным или ложным.
Высказывание истинно, если соответствует реальной ситуации, и ложно, если не соответствует ей. «Истина» и «ложь» представляют собой истинные значения высказывания.
Вспомогательные слова «и», «либо, либо», «если, то» называют логическими связками. Сложные высказывания можно строить с помощью логических связок. Так, из высказываний «светит солнце» и «идет дождь» можно образовать сложные высказывания типа «если светит солнце, то идет дождь», «светит солнце и идет дождь» и т. п.
Укажем самые важные способы построения сложных высказываний. Отрицанием называется такая логическая связка, с помощью которой из данного высказывания получается высказывание с противоположным логическим значением.
Обозначим высказывания буквами А, В, С,…, отрицание высказывания — символом
. Тогда если высказывание А истинно, то его отрицание
А ложно, и если А ложно, его отрицание
А истинно. Например, отрицанием высказывания «три является четным числом» служит высказывание «три не является четным числом».
Сложное высказывание, полученное с помощью двух (или более) высказываний при помощи слова «и», называется конъюнкцией. Заменяя слово «и» на «или» в предыдущем определении, получаем дизъюнкцию высказываний.
Высказывания, получаемые описанными способами, представляют собой предмет изучения логики высказываний. Она предполагает, что любое высказывание имеет свое логическое значение, зависящее от значений простых высказываний, входящих в него, а также и от характера их связи.
При помощи таблиц истинности в случае любого сложного высказывания можно определить, при каких значениях истинности входящих в него простых высказываний это высказывание истинно, а при каких — ложно.
Важнейшим предметом изучения логики высказываний служат логические законы, высказывания, имеющие истинные значения независимо от логических значений его составляющих.
Логика высказываний — это теория логических связей высказываний, не зависящих от внутреннего строения простых высказываний; это совокупность формул или сложных высказываний, записанных на специальном языке, включающем множество переменных: А, В, С,…, А1, В1, С1…, представляющих высказывания; особые символы для логических связок, например &, ∧ — «и»,
«неверно, что», «или», и скобки, играющие роль знаков препинания.
Логика высказываний не занимается анализом внутренней структуры простых высказываний, считая их неразложимыми.
Для определения структуры высказываний вводится список индивидных переменных: х, у, z…, х1, у1, z1…., представляющих разные объекты, и перечень предикатных переменных: Р, Q, R,…, Р1, Q1, R1,…, представляющих свойства и отношения объектов. Наряду с этими переменными могут рассматриваться индивидные константы, имена собственные.
Запись (x) Р(х) означает «любой х обладает свойством Р», (∃х) Р(х) — «существует х, обладающий свойством Р», (∃x) Q(x, у) — «существует х, который находится в отношении Q с у» и т. д.
Под предикатом понимается языковое выражение, обозначающее некоторое свойство или отношение. Предикат, указывающий на свойство предмета, например «быть круглым», называется одноместным. Двухместным, трехместным называется предикат, обозначающий отношение, в зависимости от числа его членов. Например, «кусает» — двухместный предикат, «находится посередине» — трехместный.
Предикатами называются функции, значениями которых служат высказывания. Данные функции превращаются в высказывания после подстановки имен вместо переменных.
Функцией одной переменной, например, становится выражение «…есть золотой» и т. д. В логике предикатов существуют логические операторы ∀ («для всех», «для любого», «для каждого») и ∃(«для некоторых», «существует»), называемые кванторами общности и существования соответственно.
Логика предикатов — раздел современной логики, в котором описываются выводы, учитывающие внутреннюю (субъектно-предикатную) структуру высказываний. Логика предикатов представляет собой расширение логики высказываний, поскольку все законы логики высказываний служат также законами логики предикатов, однако не наоборот.
Логика высказываний



Введение в математическую логику
Логика, созданная как наука Аристотелем (384–322 г. до н.э.), на протяжении столетий использовалась для развития многих областей знания, включая теологию, философию, математику.
Она – тот фундамент, на котором построено все здание математики. По сути, логика — это наука о рассуждениях, которая позволяет определить истинность или ложность того или иного математического утверждения, исходя из совокупности первичных предположений, называемых аксиомами. Логика применяется также в информатике для построения компьютерных программ и доказательства их корректности. Понятия, методы и средства логики лежат в основе современных информационных технологий. Одна из основных целей этой работы — изложить основы математической логики, показать, как она используется в информатике, и разработать методы анализа и доказательства математических утверждений.
Понятие высказывания
Высказывание — это утверждение или повествовательное предложение, о котором можно сказать, что оно истинно или ложно. Иными словами, утверждение об истинности или ложности высказывания должно иметь смысл. Истинность или ложность, приписываемые некоторому утверждению, называются его значением истинности, или истинностным значением.
Например, высказывания Дважды два четыре и Город Челябинск находится в азиатской части России истинные, а высказывания Три больше пяти и Река Дон в настоящее время впадает в Каспийское море ложны, так как не соответствуют действительности. Истинные высказывания принято обозначать T (true) или И (истина), а ложные, соответственно, F (false) или Л (ложь). В информатике истинность принято обозначать 1 (двоичная единица), а ложность – 0 (двоичный ноль).
Вот примеры предложений, не являющихся высказываниями:
Прочтите эту главу до следующего занятия (приказ или восклицание),
Это утверждение ложно (внутренне противоречивое утверждение),
Площадь отрезка меньше длины куба (нельзя сказать истинно это предложение или ложно, т.к. не имеет смысла).
Мы будем обозначать высказывания буквами латинского алфавита р, q, r, Например, р может обозначать утверждение Завтра будет дождь, а q — утверждение Квадрат целого числа есть число положительное.
Логические связки
Пусть р и q обозначают высказывания
р: Джейн водит автомобиль,
q: У Боба русые волосы.
Джейн водит автомобиль и у Боба русые волосы состоит из двух частей, объединенных связкой и. Это высказывание может быть символически записано в виде
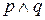
где символ 
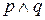
Встречаются также следующие варианты записи конъюнкции:
Точно так же высказывание
Джейн водит автомобиль или у Боба русые волосы.
символически выражается как
где 

Опровержение, или отрицание высказывания p обозначается через
Таким образом, если р есть высказывание Джейн водит автомобиль, то 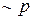
Если r есть высказывание Джо нравится информатика, то Джейн не водит автомобиль и у Боба русые волосы или Джо любит информатику символически запишется как
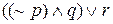
И наоборот, выражение
это символическая форма записи высказывания Джейн водит автомобиль, у Боба волосы не русые и Джо нравится информатика.
Рассмотрим выражение 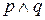
Возможны четыре случая, которые нам необходимо рассмотреть. Высказывание р может быть истинным (Т) или ложным (F) и независимо от того, какое истинностное значение принимает р, высказывание q может также быть истинным (Т) или ложным (F). Таблица истинности перечисляет все возможные комбинации истинности и ложности сложных высказываний.
| Случай | p | q | 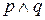 |
| T | T | T | |
| T | F | F | |
| F | T | F | |
| F | F | F |
Итак, конъюнкция 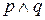
Точно так же рассмотрим высказывание Джейн водит автомобиль или у Боба русые волосы, которое символически выражается как 

| Случай | p | q |  |
| T | T | T | |
| T | F | T | |
| F | T | T | |
| F | F | F |
Дизъюнкция 
Таблица истинности для отрицания 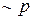
| Случай | p | 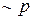 |
| T | F | |
| F | T |
Истинностное значение 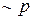
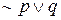


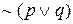
Символы 

является унарной связкой, так как применяется только к одному высказыванию.
Еще одна бинарная связка – это исключающее или, которое обозначается через 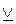
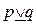
| Случай | p | q |  |
| T | T | F | |
| T | F | T | |
| F | T | T | |
| F | F | F |
Используя слово или, мы можем иметь в виду исключающее или. Например, когда мы говорим, что р — либо истина, либо ложь, то, естественно, предполагаем, что это не выполняется одновременно. В логике исключающее или используется довольно редко, и в дальнейшем мы, как правило, будем обходиться без него.
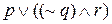
где скобки использованы, чтобы показать, какие именно высказывания являются компонентами каждой связки.
Таблица истинности дает возможность однозначно указать те ситуации, когда высказывание 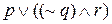
| Случай | p | q | r |  | 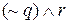 | 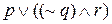 |
| T | T | T | F | F | T | |
| T | T | F | F | F | T | |
| T | F | T | T | T | T | |
| T | F | F | T | F | T | |
| F | T | T | F | F | F | |
| F | T | F | F | F | F | |
| F | F | T | T | T | T | |
| F | F | F | T | F | F |
При нахождении значений истинности для столбца 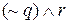



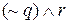

Заметим, что при определении значений истинности для столбца 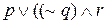
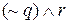

Другой, эквивалентный способ построения таблицы истинности состоит в том, чтобы записывать истинностные значения выражения под связкой. Снова рассмотрим выражение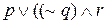
истинностные значения высказывания 
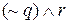

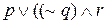

| Случай | p | q | r | p |  | (( | q) |  | r |
| T | T | T | T | T | F | T | F | T | |
| T | T | F | T | T | F | T | F | F | |
| T | F | T | T | T | T | F | T | T | |
| T | F | F | T | T | F | F | F | F | |
| F | T | T | F | F | F | T | F | T | |
| F | T | F | F | F | F | T | F | F | |
| F | F | T | F | T | T | F | T | T | |
| F | F | F | F | F | F | F | F | F |
1.1.3. Условные высказывания
Допустим, некто утверждает, что если случится одно событие, то случится и другое. Предположим, отец говорит сыну: «Если в этом семестре ты сдашь все экзамены на «отлично», я куплю тебе машину«. Заметьте, что высказывание имеет вид: если р, то q, где р — высказывание В этом семестре ты сдашь все экзамены на «отлично», а q — высказывание Я куплю тебе машину. Сложное высказывание мы обозначим символически через 
Самое мягкое, что можно сказать об отце в таком случае, — это то, что он солгал. Следовательно, если р истинно, а q ложно, то 

Поскольку студент не выполнил свою часть соглашения, отец тоже свободен от обязательств. Таким образом, если р и q ложны, то 
Таким образом, таблица истинности для высказывания 
| Случай | p | q |  |
| T | T | T | |
| T | F | F | |
| F | T | T | |
| F | F | T |
Символ 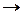
Может показаться, что 
если p, то q или как 
То, что Джейн управляет автомобилем, никак причинно не связано с тем, что Боб русоволосый. Однако нужно помнить, что истинность или ложность бинарного сложного высказывания зависит только от истинности составляющих его частей и не зависит от наличия или отсутствия между ними какой-либо связи.
Рассмотрим следующий пример. Требуется найти таблицу истинности для выражения
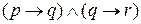
Используя таблицу истинности для 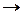

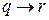
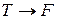
Теперь используем таблицу для 
| Случай | p | q | r | (p | 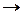 | q) |  | (q | 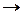 | r) |
| T | T | T | T | T | T | T | T | T | T | |
| T | T | F | T | T | T | F | T | F | F | |
| T | F | T | T | F | F | F | F | T | T | |
| T | F | F | T | F | F | F | F | T | F | |
| F | T | T | F | T | T | T | T | T | T | |
| F | T | F | F | T | T | F | T | T | F | |
| F | F | T | F | T | F | T | F | F | T | |
| F | F | F | F | T | F | T | F | T | F | |
| * |
Высказывание вида 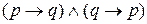
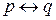
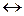
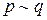
Очевидно, таблица истинности для 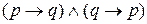
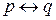
Может возникнуть вопрос о том, как интерпретировать такие выражения, как 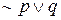
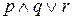
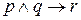
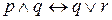
, 

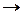
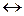

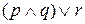
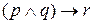
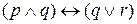
Эквивалентные высказывания
Особый интерес представляют сложные высказывания, имеющие различное строение, но являющиеся истинными в одних и тех же случаях. Такие высказывания называются логически эквивалентными. Эквивалентность двух высказываний легко установить посредством сравнения их таблиц истинности.
Рассмотрим сложные высказывания 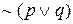

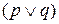
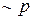


Итак, во всех четырех строках истинностные значения для 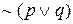

Эквивалентность — очень полезное свойство; используя его, можно строить отрицание высказываний с «или», осуществляя отрицание каждой из его частей и меняя «или» на «и».
С условным высказыванием — импликацией 


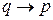
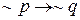

Пусть дано высказывание-импликация Если он играет в футбол, то он популярен. Для этой импликации имеем:
конверсия: Если он популярен, то он играет в футбол
инверсия: Если он не играет в футбол, то он не популярен
контрапозиция: Если он не популярен, то он не играет в футбол
Важно понимать, что высказывания Если он живет в Детройте, то Боб навестит его и Боб навестит его, если он живет в Детройте по сути являются одним и тем же высказыванием. Однако высказывание Если Боб навестит его, то он живет в Детройте не совпадает с предыдущими высказываниями. Не важен порядок, в котором р и q присутствуют в предложении, а важно, какая часть предложения является частью «если», а какая часть является частью «то». Может показаться, что при замене если р, то q на q, если р получается конверсия, но с логической точки зрения последнее высказывание совпадает с исходным.
Эквивалентность и контрапозиция условных высказываний имеют в математике большое значение. Зачастую гораздо легче доказать теорему от противного, чем дать ее прямое доказательство. Используя эквивалентность импликации и ее контрапозиции, нетрудно показать, что конверсия и инверсия импликации имеют одну и ту же таблицу истинности. В то же время импликация и ее конверсия (или инверсия) имеют различные таблицы истинности.
Используя таблицы истинности, можно доказать следующие логические эквивалентности:
а) Законы идемпотентности
б) Закон двойного отрицания
в) Законы де Моргана
г) Свойства коммутативности
д) Свойства ассоциативности