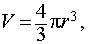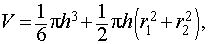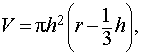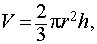Что такое высота сегмента
Что такое высота сегмента
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:
O — центр круга, OA — радиус круга.
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
| D = 2r, значит r = | D | . |
| 2 |
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | ) 2 = π | D 2 | = π | D 2 | . |
| 2 | 2 2 | 4 |
Сектор круга. Площадь сектора
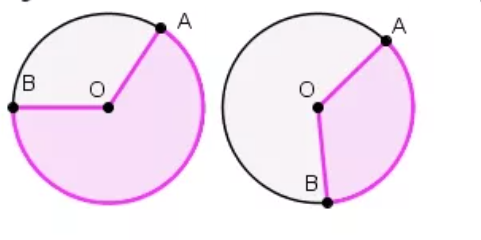
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Формула площади сектора:
| S = | πr 2 | · n = | πr 2 n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
можно представить в виде произведения
| πr 2 n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.
Площадь сегмента AMB будет вычисляться по формуле:
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
Нахождение площади сегмента круга
В данной публикации мы рассмотрим определение сегмента круга и формулы, с помощью которых можно вычислить его площадь (через радиус и центральный угол кругового сектора). Также разберем примеры решения задач для демонстрации практического применения формул.
Определение сегмента круга
Сегмент круга – это часть круга, которая ограничена дугой окружности и ее хордой.
Хорда – это часть прямой (секущей), которая пересекает круг. Концы хорды соединяются с центром круга, в результате чего образуется равнобедренный треугольник, боковые стороны которого являются радиусом окружности. Если к этом треугольнику добавить сегмент, получится сектор.
Формулы нахождения площади кругового сегмента
Через радиус и центральный угол в градусах
α° – угол в градусах.
Через радиус и угол сектора в радианах
αрад – угол в радианах.
Примеры задачи
Задание 1
Найдите площадь сегмента круга, если его радиус равен 8 см, а центральный угол сектора, стягивающего сегмент, составляет 45 градусов.
Решение
Воспользуемся первой формулой, подставив в нее известные значения:
Решение
В данном случае мы можем получить радиус из формулы, в которой задействован угол в радианах:
Окружность и круг
теория по математике 📈 планиметрия
Определения
Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.
На рисунке центр окружности обозначен точкой О.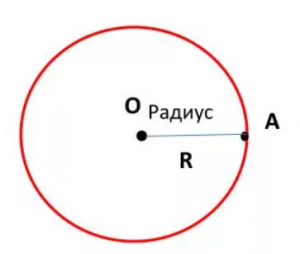 
Определения
Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.
Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.
Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.
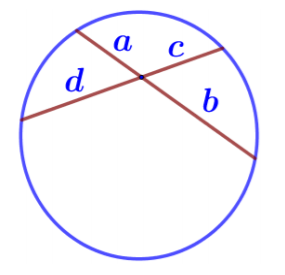
Свойство хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.
Длина окружности
Длину окружности можно вычислить по формуле:
C=2πR, где π=3,14.
Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.
Дуга, касательная, круг, сектор, сегмент
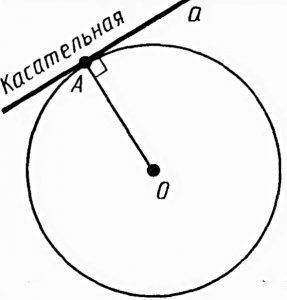
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).
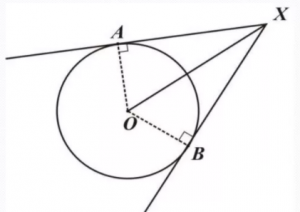
Свойства касательной
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.
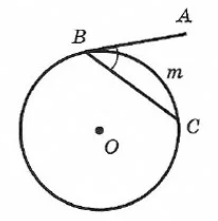
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.
Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.
Площадь круга вычисляется по формуле:
Сектор и его площадь
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.
Площадь кругового сектора вычисляется по формуле:
Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.
Как определить радиус дуги или сегмента круга и найти центр
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки», поэтому здесь лишь приведу основные формулы:
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Я достаточно подробно ответил на ваш вопрос в статье «Расчет арочной перемычки», где вы задали подобный вопрос.
Сначала термины:
Отрезок, соединяющий концы дуги называется хордой (a), а высота сегмента (перпендикуляр из середины хорды) — стрелкой (h).
Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. То есть R^2=(R-h)^2+(a/2)^2.
А что касается нахождения центра, то перпендикуляры к серединам хорд пересекаются в центре!
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Сфера и шар. Площади сферы и ее частей. Объемы шара и его частей
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
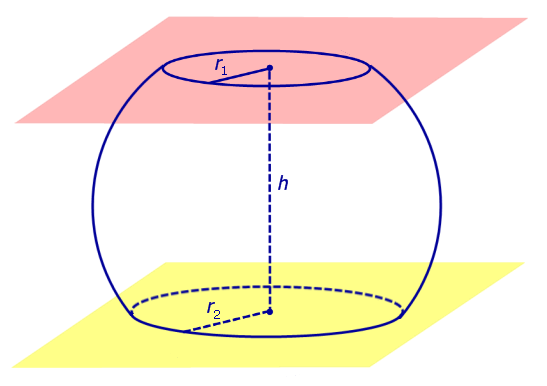
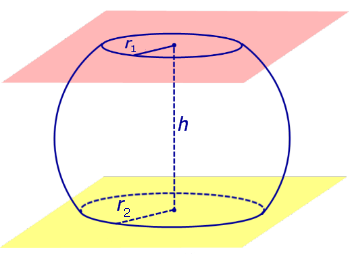
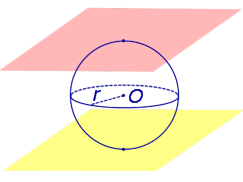
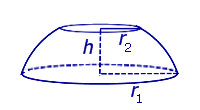
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
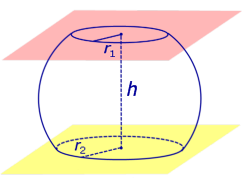
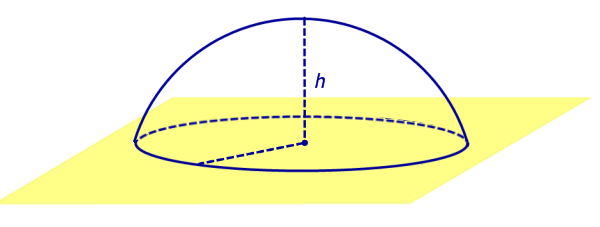
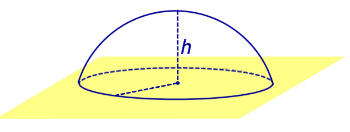
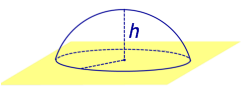
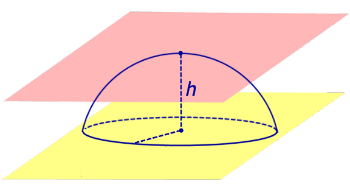
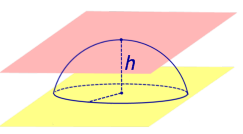
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
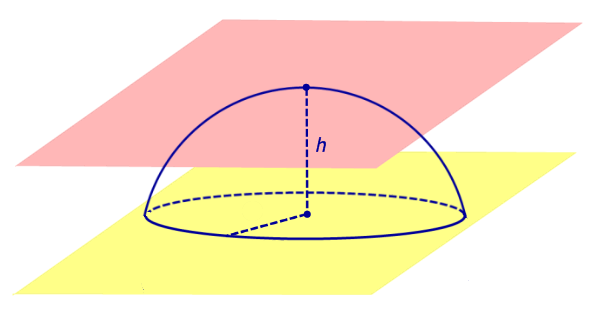
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
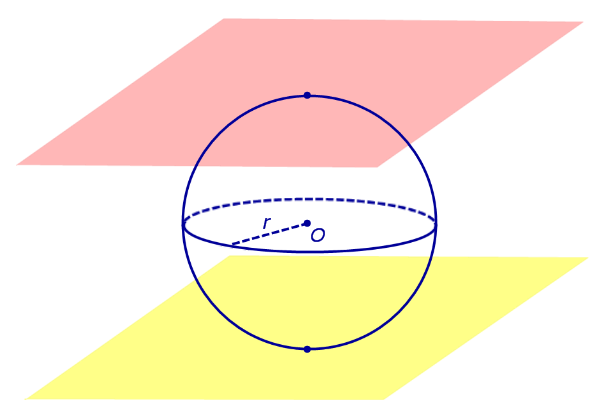
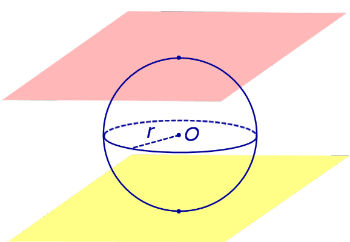
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
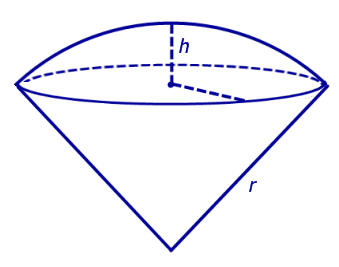
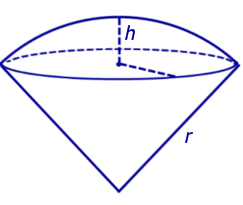
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Площади сферы и ее частей. Объемы шара и его частей
В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.
| Фигура | Рисунок | Формула | Описание |
| Сфера |  | Объем шарового сектора |
где
r – радиус сферы.
где
r – радиус шара.
Площадь сферического пояса: