Что такое высота треугольника 7 класс

Определение и свойства высоты треугольника

В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.

Определение высоты треугольника

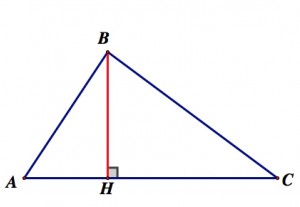
Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.

Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).

Обычно высота обозначается буквой h (иногда как h_a – это означает, что она проведена к стороне a).

Высота в разных видах треугольников

В зависимости от вида фигуры высота может:

Свойства высоты треугольника

Свойство 1

Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).

Свойство 2

При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:

Свойство 3

Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.

Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.

Свойство 4

Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.

Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.

Источник

Геометрия. 7 класс

Конспект урока

Медианы треугольника. Биссектрисы треугольника. Высоты треугольника

Перечень рассматриваемых вопросов:

Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.

Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Теоретический материал для самостоятельного изучения.

Вы уже знакомы с такими понятиями как треугольник, угол, биссектриса угла.

Разберем, как построить биссектрису треугольника, а также узнаем, что такое медиана и высота треугольника.

Начнём с понятия биссектриса угла треугольника. Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. AF – биссектриса ∠A треугольника ABC.

В любом треугольнике биссектрисы пересекаются в одной точке.

Введём понятие медианы треугольника.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

BM – медиана треугольника ABC.

В любом треугольнике медианы пересекаются в одной точке.

Введём понятие высоты треугольника.

Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

AH – высота треугольника ABC.

В любом треугольнике высоты или их продолжения пересекаются в одной точке.

Итак, сегодня мы узнали, какие отрезки называются медианой, биссектрисой, высотой треугольника, и научились их изображать с помощью чертёжных инструментов.

Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».

На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.

Докажем, что треугольники ABD и CED равны.

По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.

∠ADB = ∠CDE (по свойству вертикальных углов).

Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).

Что и требовалось доказать.

Разбор решения заданий тренировочного модуля.

В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.

1.Нарисуем рисунок по условию задачи.

2.По условию AD и BM – биссектрисы ∆ABC.

∠BAC = 50°, ∠BAC = 2∠BAO =50° → ∠BAO = 25°

∠ABC = 80°, ∠ABC= 2∠ABO = 80°→∠ABO = 40°

3.Т. к. сумма углов треугольника ABO равна 180°, то ∠ABO + ∠BAO + ∠AOB = 180°.

5.∠AOB = 180° – (25° + 40°) = 115°.

Ответ: ∠BAO = 25°, ∠ABO = 40°, ∠AOB = 115°.

В треугольнике COD: ∠O = 90°. Найдите ∠МОВ, если ОА – биссектриса угла ∠СОM, при этом ∠COА = 20°, а ВО– биссектриса ∠МОD.

1.По условию ∠СОD = 90°.

Кроме того, ОА – биссектриса угла ∠СОM → ∠МОА = ∠СОА = 20°.

2.ВО – биссектриса ∠МОD→∠ВОD = ∠МОВ.

3. ∠СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 20° + 20° + 2∠МОВ = 40° + 2∠МОВ = 90°.

Источник

Треугольник. Высота треугольника.

Высота треугольника – перпендикуляр, прочерченный из выбранной вершины треугольника на противолежащею его сторону. Для обозначения высоты треугольника используют букву h, к ней добавляется название той стороны, к которой она прочерчена: h_a, h_b, h_c,

Сторону треугольника, к которой прочерчена высота, называют основанием треугольника.

Высота треугольника может быть прочерчена к любой из трех сторон треугольника. Случается высота треугольника пересекает не само основание треугольника, а его продолжение. Так, высоты AD и ЕМ пересекают продолжения оснований ВС и FK.

Характерные особенности высоты.

В прямоугольном треугольнике высота, прочерченная из вершины прямого угла, разделит его на два треугольника, подобные первоначальному.

В остроугольном треугольнике две его высоты отделяют от него подобные треугольники.

Если треугольник остроугольный, то все основания высот принадлежат его сторонам, а у тупоугольного треугольника две высоты принадлежат продолжению сторон.

Три высоты в остроугольном треугольнике перекрещиваются в одной точке и эту точку обозначают как ортоцентр треугольника.

Источник

Способы нахождения высоты треугольника: теорема и формула

Определение высоты треугольника

Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.

Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.

Треугольники могут быть:

Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.

Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.

В геометрии высота треугольника обозначается буквой h.

В зависимости от типа треугольника высота может:

Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.

Для того чтобы определить графическое начертание высоты треугольника, необходимо:

Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.

Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:

A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B

Выглядеть графически это будет так:

Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.

Через площадь и длину стороны, к которой опущена высота:

где S — уже известная площадь треугольника,

Через длины всех сторон:

h = 2 p p × a p × b p × c a

где a, b и c — стороны треугольника,

p — его полупериметр.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длину прилежащей стороны и синус угла:

s i n a — синус угла прилежащей стороны.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через стороны и радиус описанной окружности.

Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:

где b, c — стороны разностороннего треугольника, к которым не опущена высота,

R — радиус описанной окружности.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:

где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.

Данная формула подходит только для нахождения высоты прямоугольного треугольника.

Нахождение высоты равнобедренного треугольника через основание и боковые стороны

Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.

Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.

Формула для нахождения высоты в этом случае:

b — равные боковые стороны.

Свойства высоты в равностороннем треугольнике

Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.

Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.

Высоту в таком треугольнике можно найти с помощью следующей формулы:

где а — сторона равностороннего треугольника.

Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:

а — сторона правильного равностороннего треугольника.

Нахождение высоты прямоугольного треугольника через его катеты

Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.

Важно отметить, что две другие высоты будут совпадать с катетами треугольника.

Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).

Причем гипотенуза также легко находится через катеты по теореме Пифагора:

Расчет высоты идет следующим образом:

где a, b и c — вышеупомянутые стороны треугольника.

Источник

Элементы треугольника. Высоты

Определение

Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника.

Свойства

1. Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон

2. Высоты треугольника (или их продолжения) пересекаются в одной точке, называемой ортоцентром

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному

4. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники

Некоторые формулы, связанные с высотой треугольника

где — площадь треугольника, — длина стороны треугольника, на которую опущена высота

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник