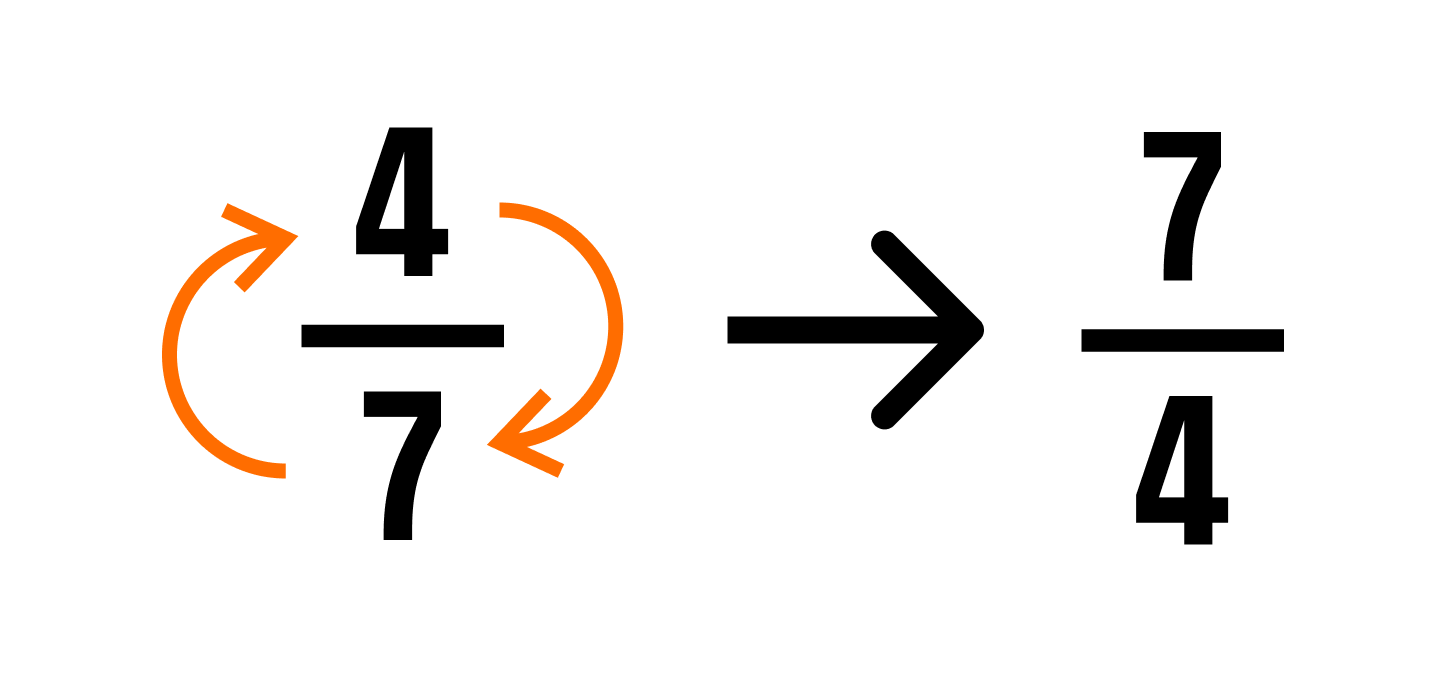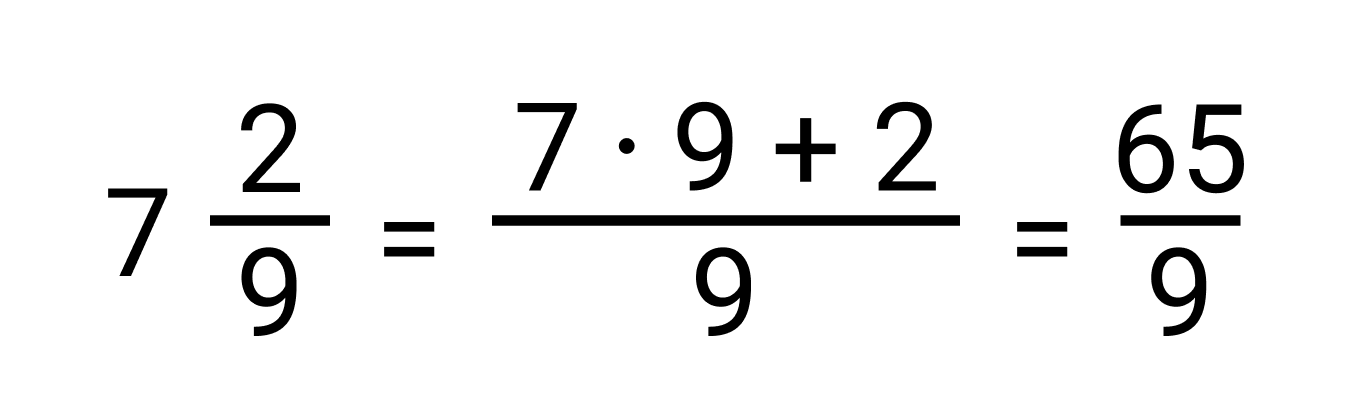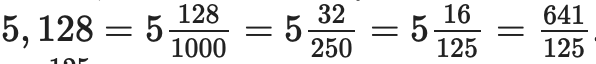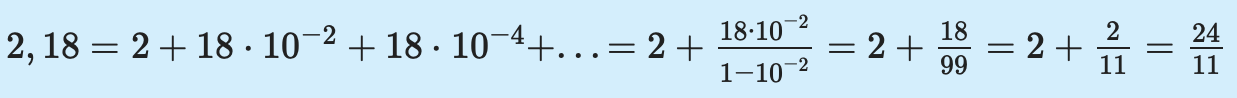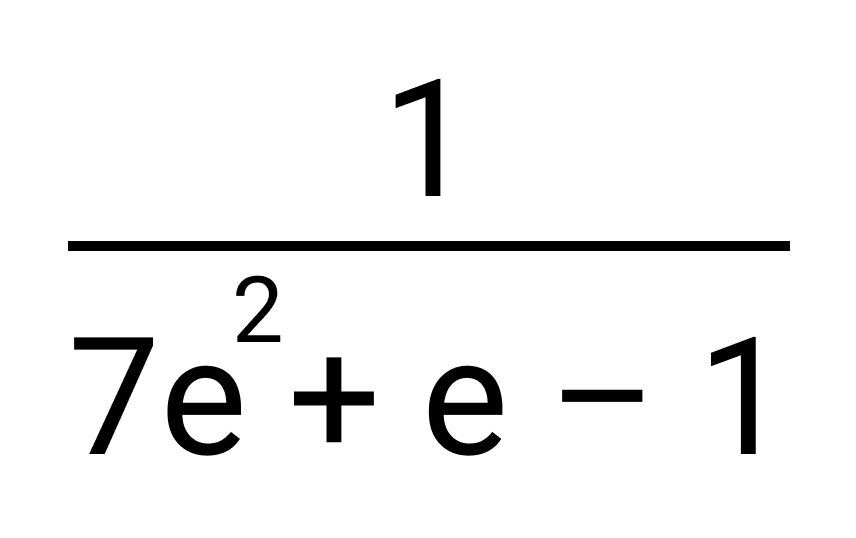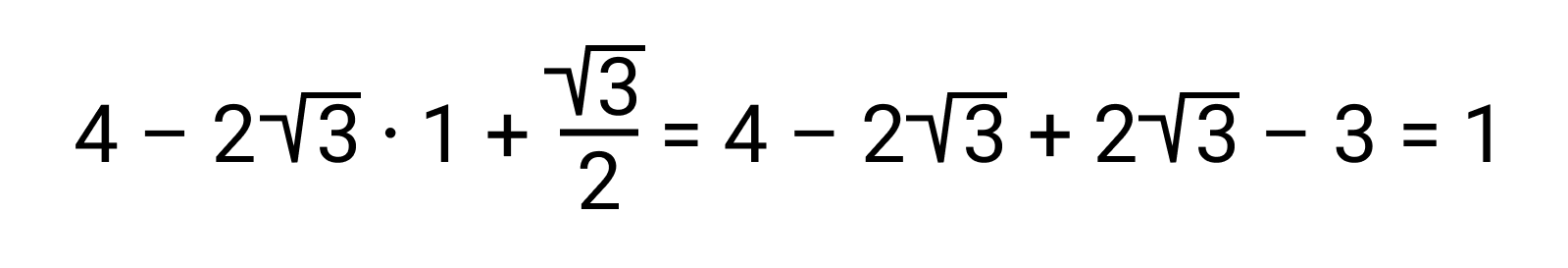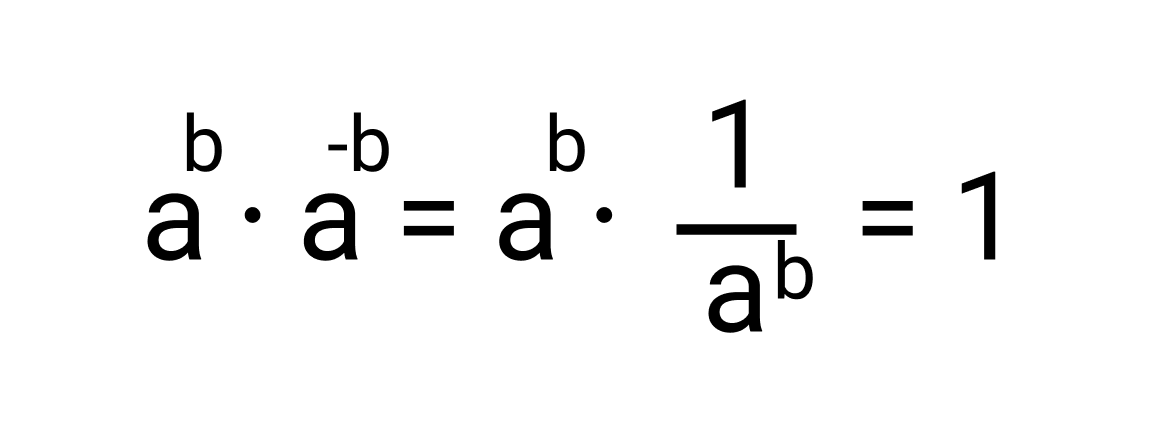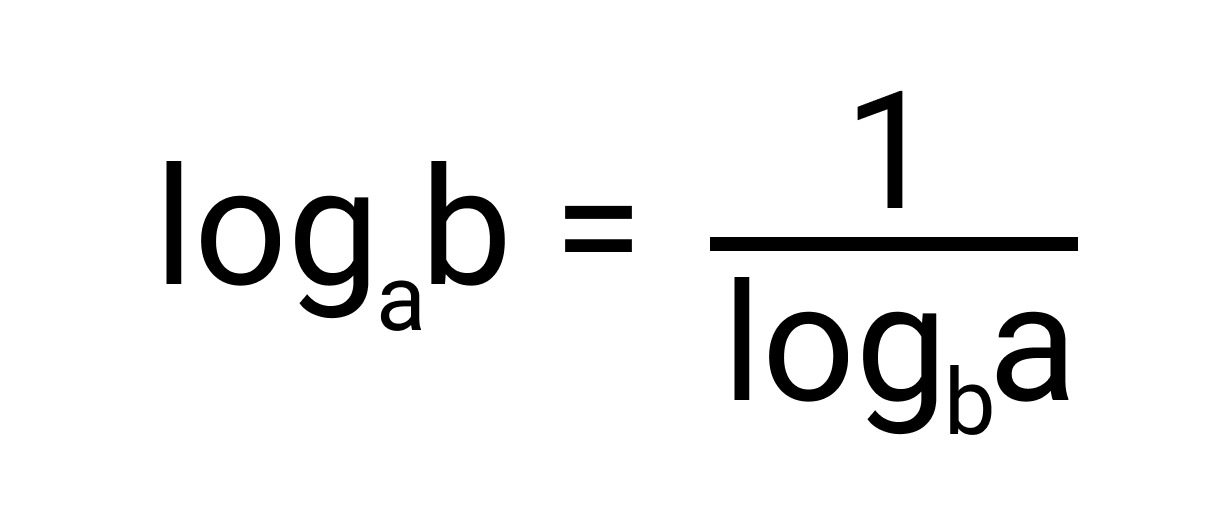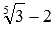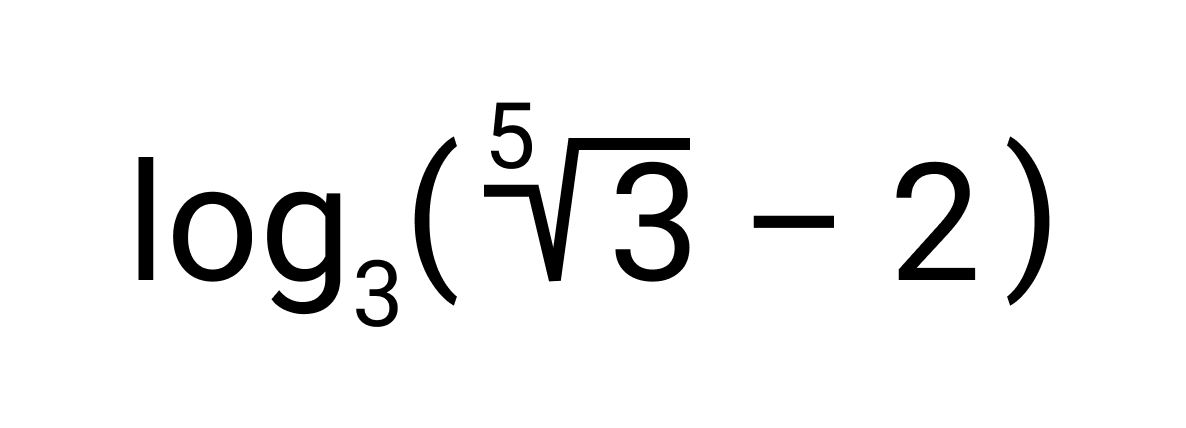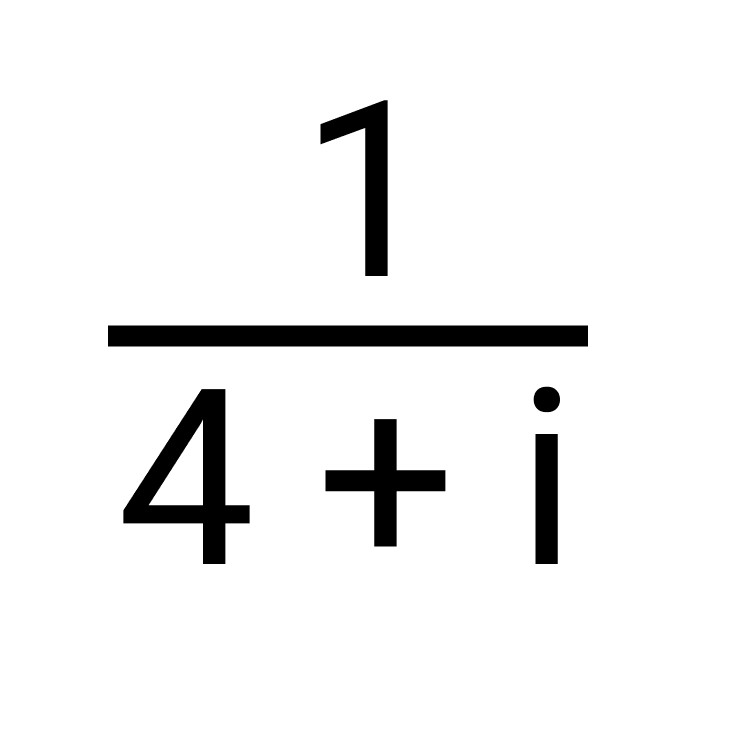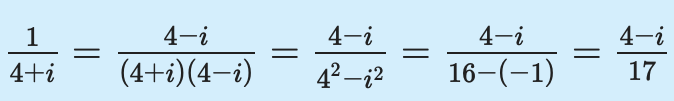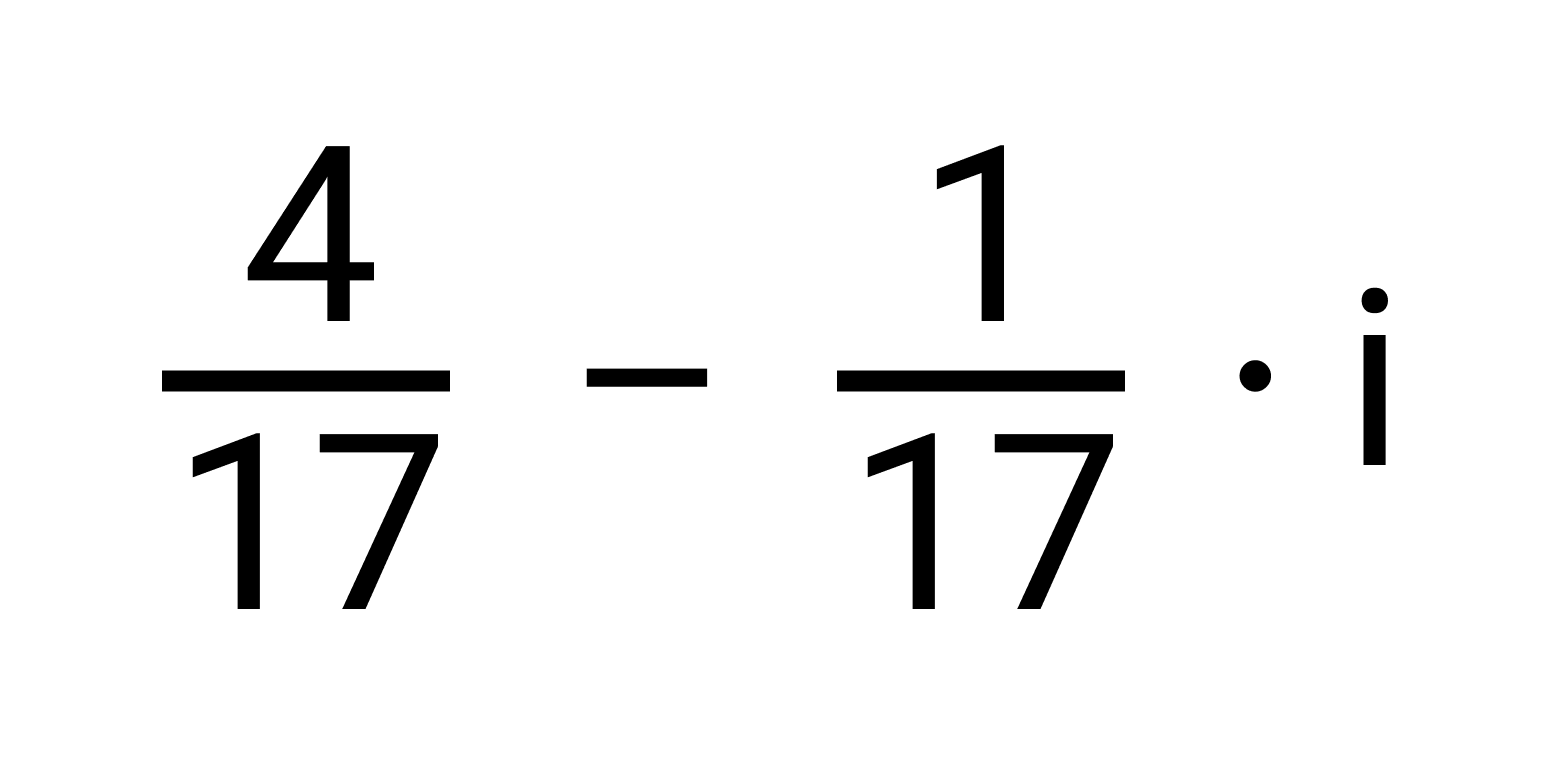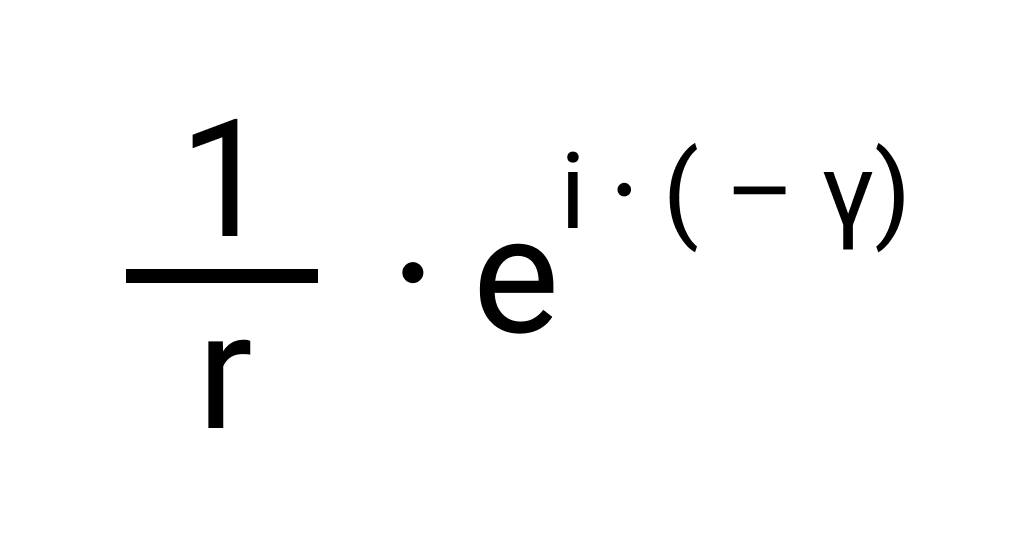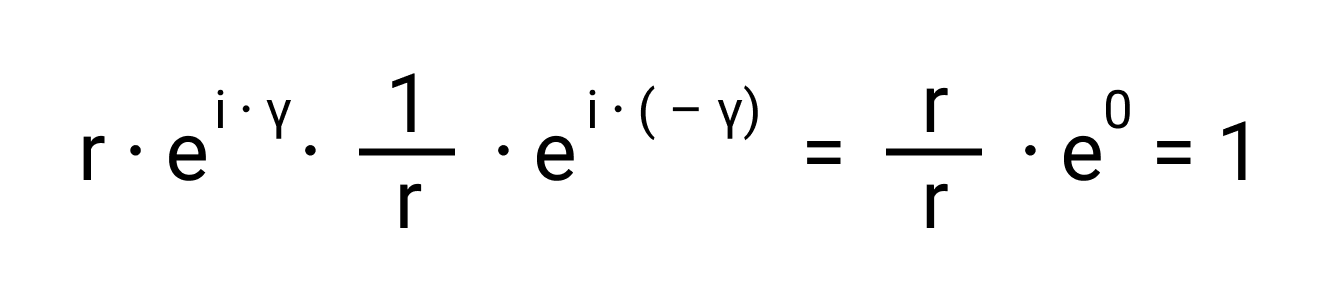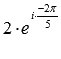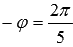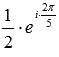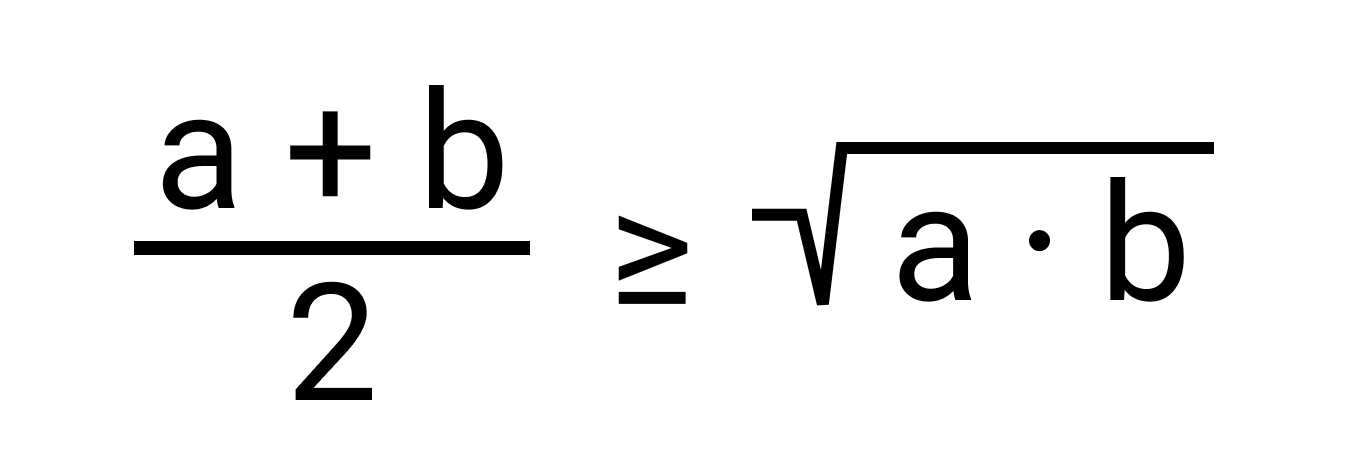Что такое взаимно обратные отрицательные числа

Взаимно обратные числа и их объяснение в математике 6 класса

При сокращении выражений дробного типа ученики иногда сталкиваются с понятием «взаимно обратных чисел». В математике 6 класса эта тема рассматривается подробнее, поскольку количество задач на упрощение тождеств увеличивается по следующим причинам, а именно: доказательства теорем и различных соотношений, выведение формул и выполнение операций вычисления. Специалисты сначала рекомендуют изучить теорию, а затем переходить к практике.

Общие сведения

Одним из правил сокращения выражений или, как называют эту операцию математики, упрощение является работа со взаимно обратными величинами. Чтобы понять суть термина, специалисты рекомендуют разобраться в основном отличии числа от цифры. Это связано с тем, что ученики постоянно путаются в терминологии и заучивают неправильные понятия. Данные действия могут привести к ухудшению понимания самой дисциплины (математики) в целом.

Следует отметить, что математика — точная дисциплина, в которой недопустимы погрешности в определении терминах, формулах и при расчетах. Например, некоторые ученики считают, что величины «3» и «-3» являются взаимнообратными значениями. На самом деле это не так, поскольку у них другое название — противоположные. Эти два термина существенно отличаются.

Взаимно обратные значения

Для понимания темы взаимно обратных величин необходимо рассмотреть определение, которое поможет выяснить, какие из них можно отнести к этому типу. Взаимно обратными называются значения, произведения которых эквивалентно единице. В математической форме запись имеет следующий вид: а * 1/а = 1.

Расшифровывается определение для чайников следующим образом: число обратное числу «а» эквивалентно величине правильной дроби, числитель которой равен 1, а знаменатель этой величине, т. е. 1/а.

Следует отметить, что обратное число 1 является единица. Это утверждение очень просто доказать. Для этого необходимо по формулировке определения представить взаимообратные величины, т. е. 1 * 1/1 = 1 * 1 = 1. Далее необходимо разобрать пример решения задачи.

Пример задачи

Задание сводится к обыкновенной теореме, в которой нужно вывести формулу суммы обратных величин. В 6 классе на уроке математики можно найти решение этой задачи. Однако не для всех учеников понятен сам процесс выведения соотношения. Решать задачу следует таким образом:

В итоге теорему о сумме обратных выражений можно сформулировать следующим образом: сумму взаимно обратных математических элементов необходимо рассматривать в виде обыкновенной дроби, числитель которой соответствует искомому числу, а знаменатель — квадрат исходного компонента, увеличенного на единицу.

Таким образом, взаимно обратными выражениями называются числовые значения, произведение которых эквивалентно единице.

Источник

Взаимно обратные числа, нахождение обратного числа.

Дадим определение и приведем примеры взаимно обратных чисел. Рассмотрим, как находить число, обратное натуральному числу и обратное обыкновенной дроби. Помимо этого, запишем и докажем неравенство, отражающее свойство суммы взаимно обратных чисел.

Взаимно обратные числа. Определение

Как найти число, обратное данному

Для натуральных чисел и обыкновенных дробей найти обратное число довольно просто. Можно сказать, даже очевидно. В случае нахождения числа, обратного иррациональному или комплексному числу, придется произвести ряд вычислений.

Рассмотрим наиболее часто встречающиеся на практике случаи нахождения обратного числа.

Число, обратное обыкновенной дроби

Число, обратное натуральному числу

Отдельное внимание стоит уделить единице, так как это единственное число, обратное число для которого равно ему самому.

Других пар взаимно обратных чисел, где обе составляющие равны, не существует.

Число, обратное смешанному числу

Число, обратное десятичной дроби

Десятичная дробь также можно представить в виде обыкновенной дроби. Нахождение обратного десятичной дроби числа сводится к представлению десятичной дроби в виде обыкновенной дроби и нахождению обратного числа для нее.

Рассмотрим еще один пример.

Пример. Нахождение числа, обратного десятичной дроби

Переводим десятичную дробь в обыкновенную:

Аналогично и для иррациональных чисел, отвечающим непериодическим бесконечным дробям, обратные числа записываются в виде дробных выражений.

Взаимно обратные числа с корнями

Обратимся к практике.

Пример. Взаимно обратные числа с корнями

Чтобы узнать, являются ли числа взаимно обратными, вычислим их произведение.

Произведение равно единице, значит, числа взаимно обратны.

Рассмотрим еще один пример.

Пример. Взаимно обратные числа с корнями

Взаимно обратные числа со степенями

Пример. Взаимно обратные числа со степенями

Взаимно обратные числа с логарифмами

Пример. Взаимно обратные числа с логарифмами

Число, обратное комплексному числу

Как уже отмечалось ранее, определение взаимно обратных чисел справедливо не только для действительных чисел, но и для комплексных.

Пример. Число, обратное комплексному числу

Помимо алгебраической формы, комплексное число может быть представлено в тригонометрической или показательной форме следующим образом:

z = r · cos φ + i · sin φ

Соответственно, обратное число будет иметь вид:

Рассмотрим примеры с представлением комплексных чисел в тригонометрической и показательной форме.

Пример. Найти число, обратное комплексному числу

Ответ: 1 2 · e i 2 π 5

Сумма взаимно обратных чисел. Неравенство

Существует теорема о сумме двух взаимно обратных чисел.

Сумма взаимно обратных чисел

Приведем доказательство теоремы. Как известно, для любых положительных чисел a и b среднее арифметическое больше или равно среднему геометрическому. Это можно записать в виде неравенства:

a + 1 a 2 ≥ a · 1 a a + 1 a ≥ 2

Что и требовалось доказать.

Приведем практический пример, иллюстрирующий данное свойство.

Пример. Найти сумму взаимно обратных чисел

Вычислим сумму чисел 2 3 и обратного ему числу.

2 3 + 3 2 = 4 + 9 6 = 13 6 = 2 1 6

Как и говорит теорема, полученное число больше двух.

Источник

Взаимно обратные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение взаимно обратных чисел

С предыдущих уроков математики мы знаем: если прибавить или вычесть из числа нуль — оно не изменится. Точно также, если умножить или разделить число на единицу.

Ноль — нейтральный элемент для сложения и вычитания. При этом числа, которые в сумме дают ноль, называют противоположными.

Единица — нейтральный элемент для умножения и деления. Поэтому симметричными называют числа, чье произведение дает единицу.

Два числа называют взаимно обратными, если их произведение равно 1.

Обратное число к данному числу — это такое число, которое мы умножаем на данное число и получаем единицу.

Если числа a и b взаимно обратные, то можно сказать, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Также можно говорить, что числу a обратно число b, а числу b обратно число a.

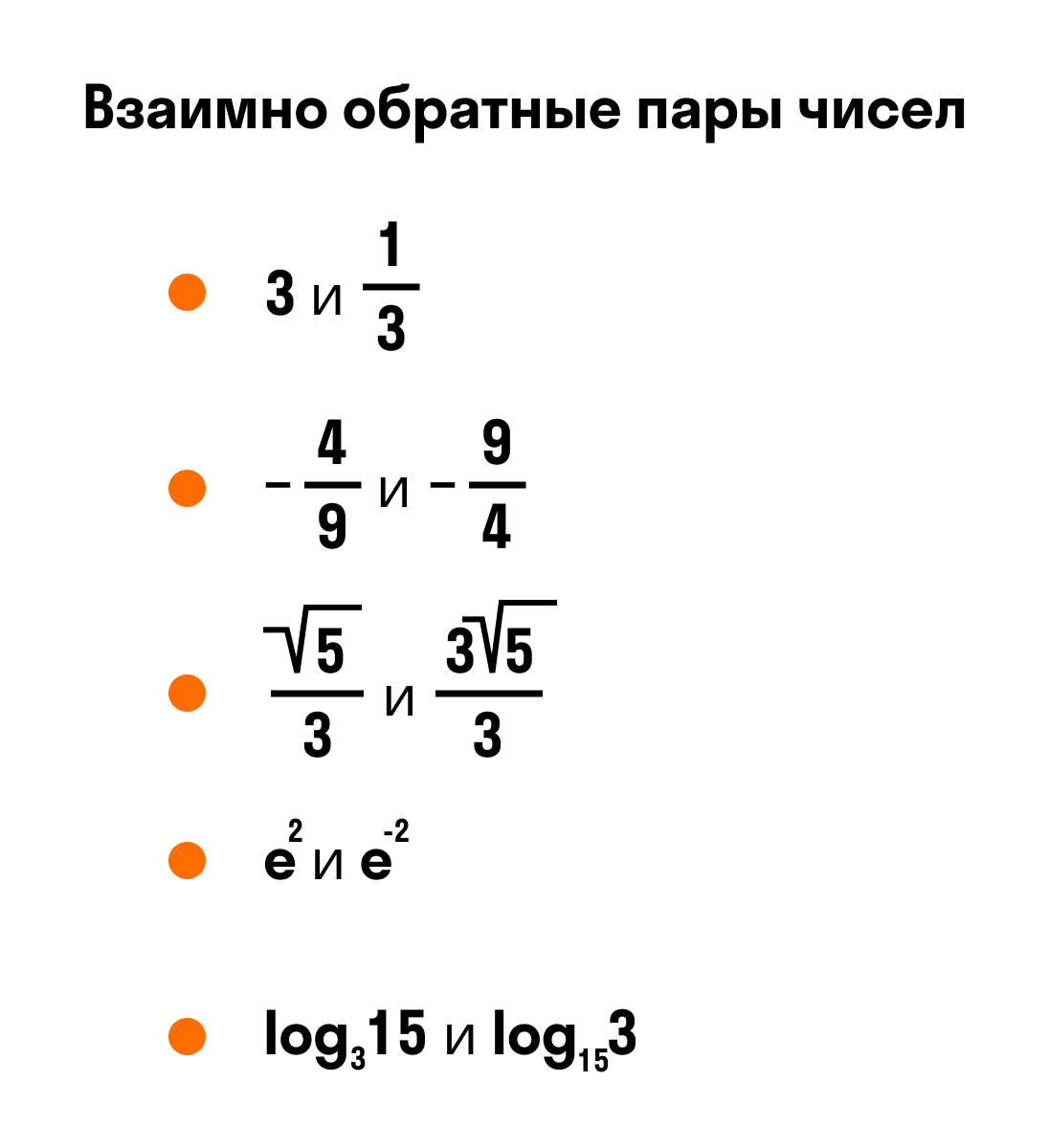
Приведем примеры взаимно обратных чисел. Так как произведение двух единиц равно 1, то по определению числа 1 и 1 — взаимно обратные.

Определение взаимно обратных чисел относится к любым числам — натуральным, целым, действительным, комплексным.

Как найти число, обратное данному числу

Иногда число, обратное данному числу, очевидно. Так бывает с натуральными числами и обыкновенными дробями. В других случаях приходится проводить вычисления. Например, с иррациональными и комплексными числами.

Рассмотрим каждый отдельный случай нахождения числа, обратного данному числу.

Число, обратное обыкновенной дроби

Числом, обратным обыкновенной дроби a/b, является дробь b/a.

Чтобы это проверить, выполним умножение обыкновенных дробей a/b и b/a — получим 1. Значит дроби a/b и b/a — взаимно обратные числа.

Если числитель и знаменатель дроби a/b поменять местами, то получится дробь b/a, обратная дроби a/b.

Это правило значительно экономит время. Можно сразу записать число, обратное данной обыкновенной дроби без каких-либо вычислений.

Число, обратное натуральному числу

Нахождение числа, обратного данному натуральному числу, можно свести к нахождению числа, обратного дроби. Для этого нужно записать натуральное число как дробь со знаменателем 1.

Пусть нам дано натуральное число n, и нужно записать число, обратное числу n. Так как натуральное число n равно дроби n/1, то, поменяв местами числитель и знаменатель этой дроби, получим дробь 1/n, которая и является числом, обратным натуральному числу n.

Итак, натуральному числу n обратным числом является число 1/n, то есть, дробь с числителем 1 и знаменателем n. Значит n и 1/n — взаимно обратные числа.

Отдельно отметим число, обратное натуральному числу 1. Число, обратное единице, это единица. Пара взаимно обратных чисел 1 и 1 уникальна тем, что составляющие ее числа равны, других таких пар взаимно обратных чисел не существует.

Найти число, обратное смешанному числу

Напомним, что смешанное число выглядит так: A b/c. Чтобы найти число, обратное смешанному числу, нужно представить данное смешанное число в виде неправильной дроби, а уже после найти число, обратное этой дроби. Как это работает рассмотрим на примере.

Пример

Найти число, обратное смешанному числу

Сначала выполним перевод смешанного числа в неправильную дробь:

Число, обратное дроби 65/9, есть дробь 9/65. Поэтому, смешанному числу 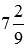обратно число 9/65.

Ответ: 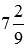и 9/65 взаимно обратные числа.

Найти число, обратное десятичной дроби

Конечную десятичную дробь или периодическую десятичную дробь можно заменить обыкновенной дробью. Поэтому найти число, обратное конечной или периодической десятичной дроби, можно через поиск числа, которое обратно обыкновенной дроби. Разберемся на примерах.

Пример 1

Найти число, которое обратно десятичной дроби 5,128.

Переведем конечную десятичную дробь в обыкновенную:

Числом, обратным полученной дроби, является обыкновенная дробь 125/641. Это и есть решение задачи.

Пример 2

Какое число является обратным для периодической десятичной дроби 2,(18)?

Переведем периодическую десятичную дробь в обыкновенную:

Обратная дробь для 24/11 — 11/24. Значит, числом, обратным исходной десятичной дроби 2,(18), является дробь 11/24.

Так как бесконечным непериодическим десятичным дробям отвечают иррациональные числа, то числа, которые обратны им, также записывают в виде дробных выражений.

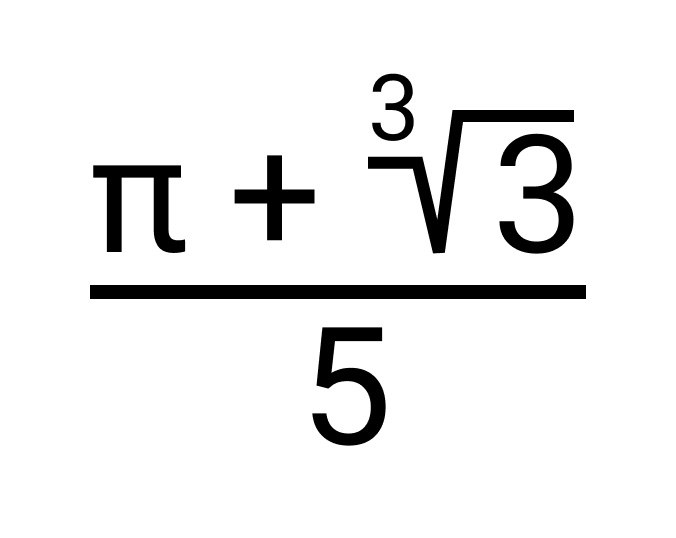
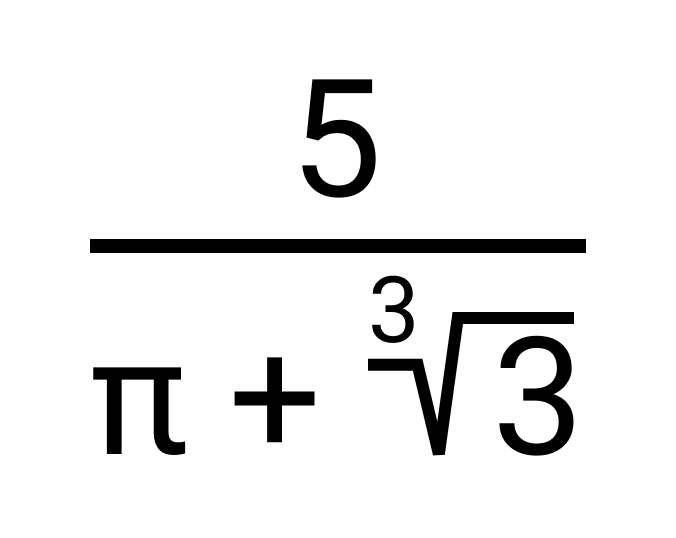
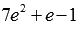
Например, иррациональному числу обратно число , а иррациональному числу обратно число

Взаимно обратные числа с корнями

Важно запомнить, что вид взаимно обратных чисел может отличаться от a и 1/a. Поэтому нужно быть внимательным. Особенно это касается чисел, записи которых содержат знак корня. Рассмотрим на примере, как это бывает.

Пример

Вычислим произведение этих чисел:

Так как в ответе мы получили единицу и мы знаем, что произведение взаимно обратных чисел равно 1, значит эти числа можно назвать взаимно обратными.

Ответ: да, число взаимно обратны.

Взаимно обратные числа со степенями

Допустим, есть число, которое равно какой-то степени числа a. То есть, число a возведено в степень b. Обратным числу ab будет число a-b. Проверим.

Пример

Взаимно обратные числа с логарифмами

У логарифма числа a по основанию b обратное число равно логарифму числа b по основанию a. То есть log _b a и log _a b — взаимно обратные числа.

Действительно, из свойств логарифма следует, что

, откуда log _b a * log _a b = 1.

Пример

Записать число, которое обратно логарифму числа 3 по основанию

Число, обратное числу 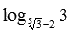, выглядит так:

Ответ:

Найти число, обратное комплексному числу

Сейчас узнаем, как находить число, обратное комплексному числу z.

Пример 1

Найти число, обратное комплексному числу 4 + i.

4 + i =

Умножим числитель и знаменатель полученного дробного выражения на число
4 + i.

Ответ:

или

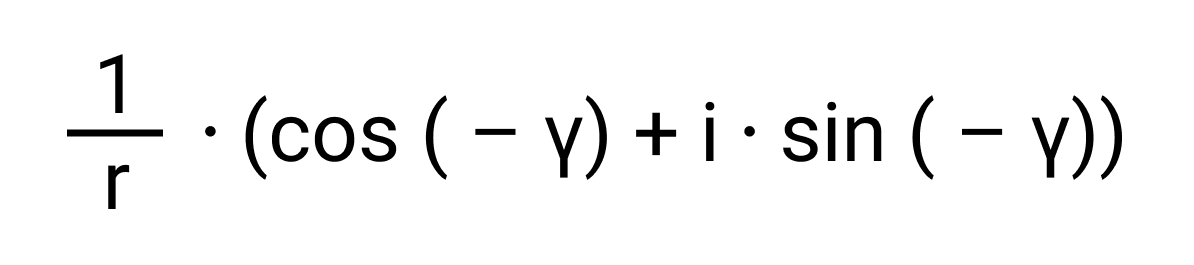
Действительно, и

Пример 2

Определить число, обратное комплексному числу

В этом примере r = 2 и 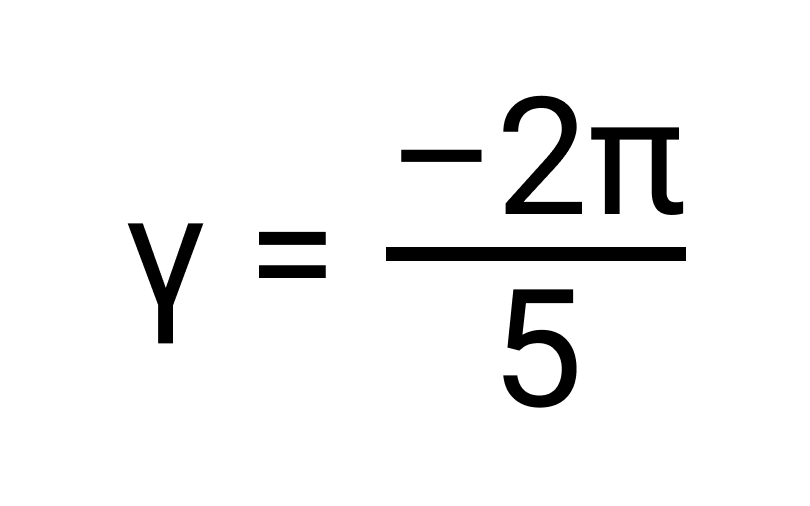, откуда 1/r = 1/2 и

Следовательно, нужное нам обратное число равно

Являются ли числа взаимно обратными? Да, мы только что это доказали.

Ответ:

Неравенство с суммой взаимно обратных чисел

В математике есть специальная теорема о сумме взаимно обратных чисел — давайте ее сформулируем и узнаем ключевое свойство.

Теорема

Сумма двух положительных взаимно обратных чисел больше или равна 2.

Доказательство теоремы:

Нам известно, что среднее арифметическое положительных чисел a и b всегда больше или равно среднему геометрическому этих чисел, то есть,

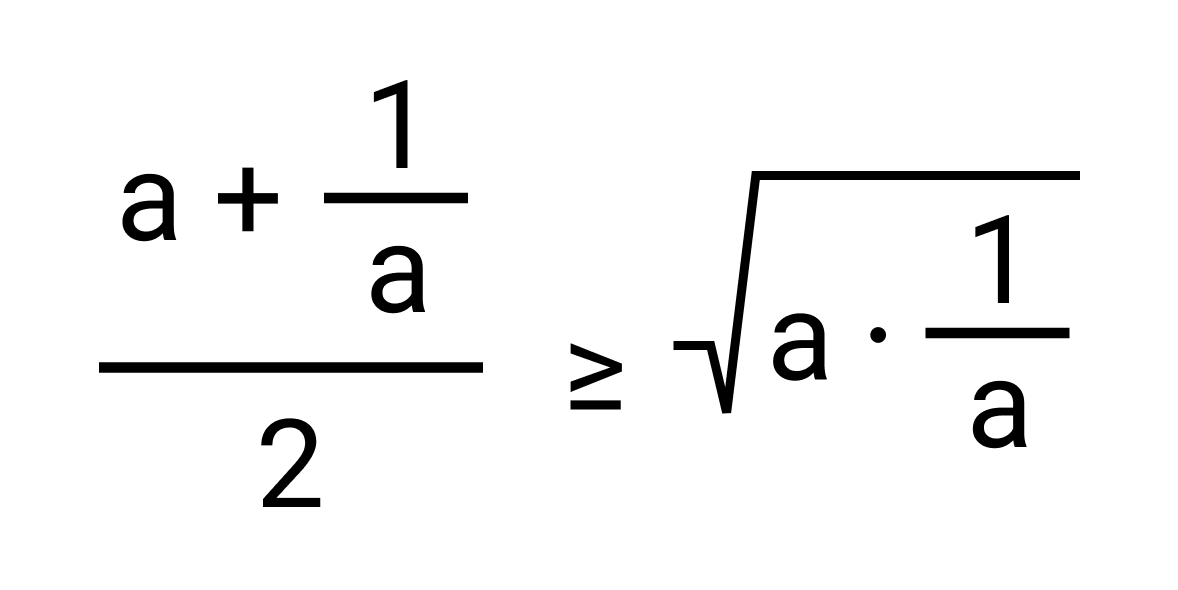
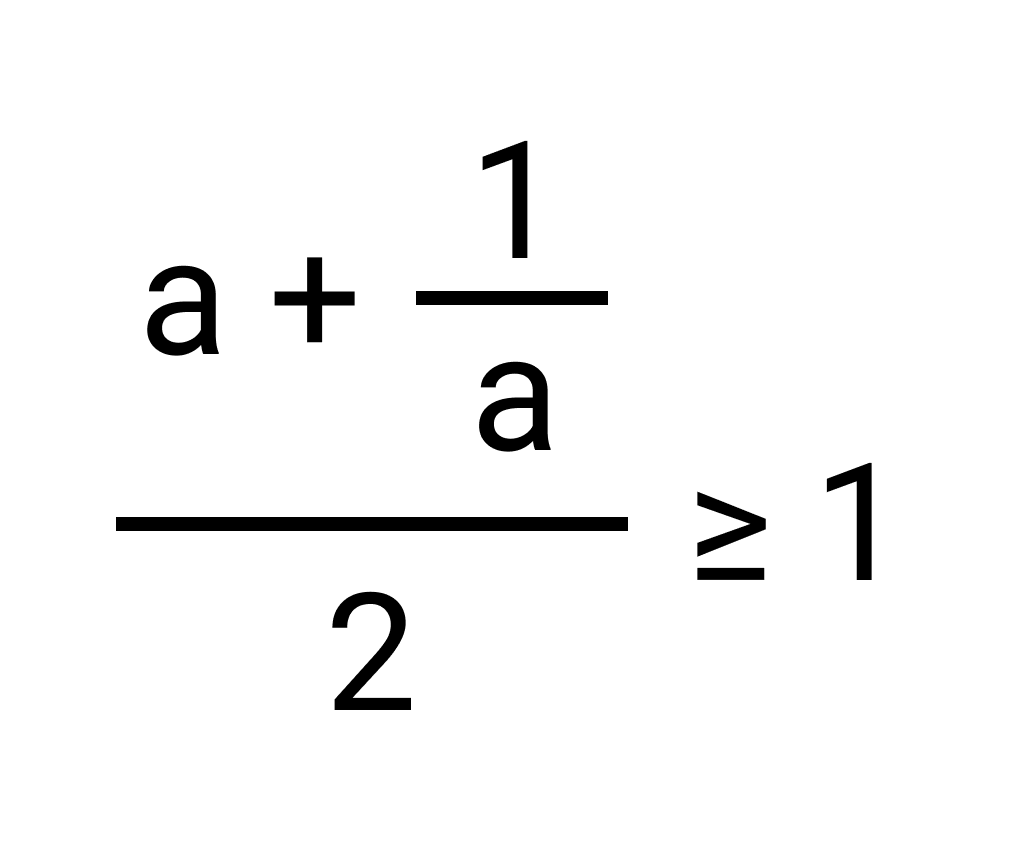
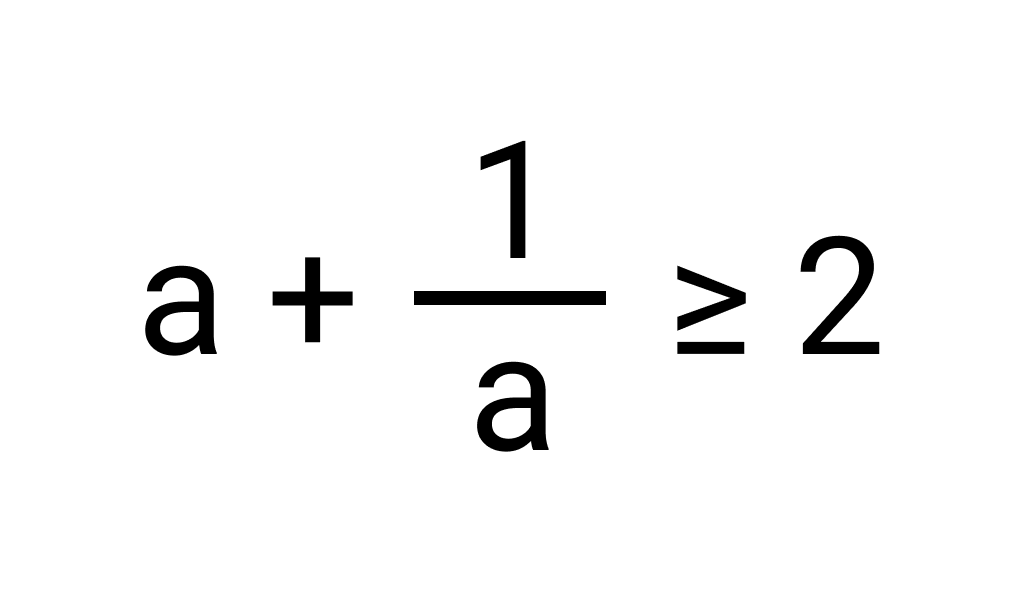
Если в качестве b мы возьмем число, обратное a, то полученное неравенство будет выглядеть так: откуда и , что и требовалось доказать.

Пример

Вычислить сумму взаимно обратных чисел 2/3 и 3/2,

Источник

Взаимно обратные числа, нахождение числа, обратного данному числу.

Сейчас мы тщательно изучим взаимно обратные числа. Сначала дадим определение и приведем примеры взаимно обратных чисел. Дальше на примерах разберем, как находится число, обратное данному числу. В частности, найдем число, обратное обыкновенной дроби, число, обратное натуральному числу, и т.п. В заключение приведем и докажем неравенство, характерное для суммы взаимно обратных чисел.

Навигация по странице.

Взаимно обратные числа, определение, примеры

Сразу дадим определение взаимно обратных чисел.

Из рассмотренных примеров взаимно обратных чисел понятно, что определение взаимно обратных чисел относится к любым числам – и к натуральным, и к целым и к действительным, и даже к комплексным.

Нахождение числа, обратного данному числу

Иногда число, обратное данному числу, очевидно, как, например, для натуральных чисел или обыкновенных дробей. В других случаях приходится проводить вычисления, как, например, при отыскании числа, обратного иррациональному числу, или обратного комплексному числу.

Остановимся на наиболее часто встречающихся случаях нахождения числа, обратного данному числу.

Число, обратное обыкновенной дроби

Число, обратное натуральному числу

Нахождение числа, обратного данному натуральному числу, можно свести к нахождению числа, обратного дроби. Для этого нужно лишь записать данное натуральное число как дробь со знаменателем 1.

Нахождение числа, обратного смешанному числу

Чтобы найти число, обратное данному смешанному числу, можно представить данное смешанное число в виде неправильной дроби, после чего найти число, обратное этой дроби. Рассмотрим применение этого правила на примере.

Найдите число, обратное смешанному числу .

и 9/65 взаимно обратные числа.

Нахождение числа, обратного десятичной дроби

Мы знаем, что конечная десятичная дробь или периодическая десятичная дробь может быть заменена обыкновенной дробью. Поэтому, нахождение числа, обратного конечной или периодической десятичной дроби, может быть сведено к нахождению числа, обратного обыкновенной дроби. Рассмотрим примеры.

Источник

Урок 17 Бесплатно Взаимно обратные числа

В этом уроке мы узнаем, какие числа называются взаимно обратными, как найти число, обратное данному, а также разберем все эти случаи для смешанных чисел.

Взаимно обратные числа

Введем определение: взаимно обратными числами называются такие два числа, произведение которых равняется единице.

То есть, если имеются две обыкновенных дроби, каждую из которых нельзя сократить, то необходимо ответить на вопрос: являются ли они взаимно обратными? Для этого достаточно проверить два равенства:

Можно не запоминать что с чем сравнивать. Если начнем записывать выражение для произведения, то заметим, что в случае взаимно обратных чисел числители и знаменатели сократятся, и результатом будет единица.

Перед сравнением важно, чтобы дроби уже были сокращены!

Допустим, имеются две дроби: \(\mathbf<\frac<2><3>>\) и \(\mathbf<\frac<6><4>>\)

Если к ним просто применить признак и сравнить по отдельности числитель первой дроби с знаменателем второй и наоборот, то мы заменим, что равенства не выполняются. Но, если их перемножить, мы заметим, что произведение равняется 1, следовательно, они являются взаимно обратными.

Итак, имеются два способа проверить, являются ли числа взаимно обратными.

Пример 1

Являются ли числа \(\mathbf<\frac<2><5>>\) и \(\mathbf<\frac<3><2>>\) взаимно обратными?

Воспользуемся вторым способом. Как можно заметить, дроби уже сокращены.

Пример 2

Являются ли числа \(\mathbf<\frac<2><5>>\) и \(\mathbf<\frac<5><2>>\) взаимно обратными?

Воспользуемся первым способом.

В процессе умножения все множители в числителе и знаменателе сократились и результатом произведения оказалась единица.

Значит \(\mathbf<\frac<2><5>>\) и \(\mathbf<\frac<5><2>>\) являются взаимно обратными.

Рассмотрим еще один момент.

Допустим, нас просят проверить, являются ли взаимно обратными два числа, одно из которых является обыкновенной дробью, а второе натуральным числом.

В таком случае нам достаточно представить натуральное число в виде дроби, у которой числитель будет равняться данному натуральному числу, а знаменатель единице.

Дальше можно действовать одним из двух разобранных способов.

Пример 3

Являются ли числа \(\mathbf<\frac<2><126>>\) и 63 взаимно обратными?

Представим 63 как обыкновенную дробь.

Далее воспользуемся вторым способом.

Теперь сравним числитель первой дроби со знаменателем второй: единица равна единице.

Сравним знаменатель первой дроби с числителем второй: 63 равно 63

Делаем вывод, что числа \(\mathbf<\frac<2><126>>\) и 63 являются взаимно обратными.

Пройти тест и получить оценку можно после входа или регистрации

Источник