Что такое взаимно обратные задачи 3 класс
Что означает обратная задача в математике?
Что такое обратная задача?
Начиная со второго класса, детям регулярно задают на дом задания. Большое внимание педагоги уделяют решению задач, ведь именно за них ребенок получает больше баллов на контрольных и тестах.
Понятие «обратная задача» знакомо всем ученикам школы, в которой учатся мои дети, даже тем, кто не любит математику и далек от нее.
В качестве примера рассмотрим задачу с решением в одно действие: На столе было 5 груш и 4 яблока, сколько фруктов было всего. Решение простое: 5+4=9.
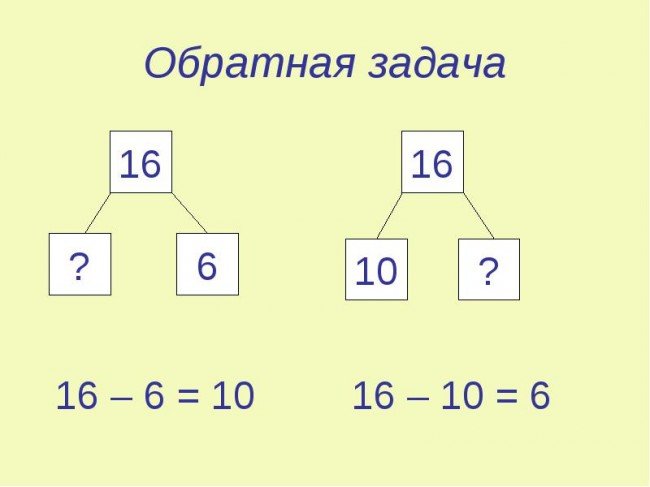
В данном случае, можно составить и решить две задачи обратные данной:
Чем больше данных в задаче, тем больше обратных задач можно к ней составить.
Обратные задачи просты и понятны большинству учеников младших классов.
Если же ваш ребенок пропустил эту тему, не понимает, что от него требуется, научить его составлять обратные задачи не составит труда, так как данная тема легко воспринимается даже детьми с гуманитарным складом ума.
Достаточно интересна и познавательна для родителей тема: «Как помочь ребенку преодолеть школьные проблемы», рекомендую с ней, по желанию, ознакомиться.
Решение взаимно-обратных задач в начальной школе (на умножение и деление)
2. Решение простых задач на умножение и деление.
Задачи на умножение, деление по содержанию и деление на равные части. Задачи на увеличение и уменьшение числа в несколько раз и задачи на кратное сравнение.
Задачи на нахождение части числа, числа по величине его части, задачи типа: “Какую часть составляет одно число от другого”.
Перед нашей школой всегда стояла задача построения такой методической системы, которая обеспечивала бы резкое повышение качества знаний при значительной экономии времени, расходуемого на изучение материала. В наше время при все возрастающем потоке информации эта проблема стоит особенно остро.
Еще в 60-е годы Комиссией по определению содержания обучения математике, работающей в АПН СССР, был разработан проект программы по математике. Авторы проекта одним из главных средств ускоренного и сознательного изучения материала в школе считали изменение структуры существующих программ, осуществление более целесообразной группировки вопросов, рациональной группировки вопросов, рациональной последовательности разделов, то есть применение метода противопоставления на уроках математики.
Общепринятая традиционная система обучения математике соблюдает принцип раздельного изучения взаимосвязанных понятий или преобразований. При одновременном изучении взаимосвязанных вопросов в пределах одних и тех же уроков дидактической единицей усвоения становится более крупная единица знаний, чем в случае раздельного изучения их. Переход в обучении к более крупным дидактическим единицам усвоения знаний дает экономию сил и времени.
При изучении задач в курсе математики, как простых, так и сложных, как обычных арифметических, так и типовых оказывается высоко эффективным систематическое применение так называемого метода обратных задач.
Успех обучения решению задач посредством преобразования прямой задачи в обратные задачи объясняется как первопричиной тем, что такой путь заставляет поднимать из сферы подсознания наибольшее разнообразие связей, заключенных в содержании задачи. Это и обеспечивает – на языке дидактики – глубокое и прочное усвоение материала.
На составление и решение обратной задачи уходит несравненно меньше времени, чем на решение новой задачи, так как числовые данные и сюжет остаются прежними; производится здесь лишь логическая операция по переосмыслению ролей чисел; неизвестное в прямой задаче становится известным и наоборот.
Поэтому я взяла для изучения и последующей работы тему “Решение взаимно обратных задач в начальной школе”.
На мой взгляд, самое трудное в начальной школе – научить ребенка грамотно писать, а самое трудное в математике – научить решать задачи.
В процессе работы мне хотелось повысить процент способных детей и уменьшить процент слабых.
Кроме того, в своей работе я стремлюсь к тому, чтобы как можно больший процент детей имел качественный показатель знаний по математике. Далее я опишу, как я этого добиваюсь и каковы результаты молей работы.
Я ознакомилась с мнением различных ученых-методистов (смотреть список литературы) по вопросу классификации задач и решению взаимно обратных задач, как по традиционной, так и по развивающей методике.
Работа со взаимно обратными задачами просматривается у Аритской Н.И., у Свечникова А.А., но у Аритской И.И. нет четкой классификации задач, также, как у Истоминой Н.Б.
Классификация сложных задач в принципе сходна у Эрдниева П.М., Свечникова А.А., Баитовой М.А. но простые задачи Свечников А.А. и Баитова М.А. классифицируют несколько иначе, чем Эрдниев П.М.
За основу я взяла работу над задачами по Эрдниеву П.М., так как на сегодняшний день более четкой классификации задач и методики работы над взаимно обратными задачами я пока не вижу.
Следует отметить существенно важные дидактические достоинства метода обратных задач:
– Во время преобразования задачи учащийся выявляет и использует взаимно обратные связи между величинами задачи:
| Прямая задача | Ц. | К. | С. |
| 30 р. | 6 к. | ? р. | |
| Обратная задача | Ц. | К. | С. |
| 30 р. | ? к. | 180 р. |
– Во время преобразования учащийся практически познает связи между действиями. Полезно, например, обратить внимание учащихся на то, что количество действий при решении прямой и обратной задач совпадает (это правило нарушается крайне редко). Кроме того, полезно знать учащимся следующее явление: каждому действию прямой задачи соответствует действие той же ступени в обратной задаче.
– Количество комбинаций при составлении обратной задачи ограниченно: оно равно количеству данных в задаче.
– Решая обратную задачу, учащийся перестраивает суждения и умозаключения, использованные при решении прямой задачи, преодолевая при этом в мышлении инерцию действий, выполненных при решении прямой задачи.
– Решение обратной задачи представляет проверку решения прямой задачи, то есть при этом возникают благоприятные условия для потоков информации по целям обратных связей в мыслительных процессах (систематическое сочетание прямых и обратных задач вырабатывает важное качество личности – чувство самоконтроля).
– Учащиеся, составляя обратные задачи, знакомятся со значительно большим разнообразием задач, чем в традиционных задачниках.
– При составлении и решении обратных задач выдвигается на первый план анализ и видоизменение математических зависимостей.
Итак, для развития мышления ценны не столько прямые и обратные задачи, взятые вне времени сами по себе, а наиболее важный познавательный элемент заключается в процессе преобразования одной задачи в другую, в сравнении условий, решений, ответов задач, то есть тех “невидимых”, трудно уловимых и трудно изобразимых при логическом анализе элементов мысли, которые связывают решения обеих задач (прямой и обратной).
Однако нельзя забывать, что переходы эти осуществляются во времени: чем меньше интервал времени между противоположными процессами решения взаимно обратных задач, тем быстрее и чаще будут совершаться эти переходы и тем прочнее будут сохраняться в памяти следы этих переходов, то есть тем более глубокими и основательными окажутся осваиваемые знания.
2. Решение задач на умножение и деление.
Связи между умножением и делением в той же мере взаимно обратны, в какой взаимно обратны действия сложения и вычитания. Классификация задач по теме: “Умножение и деление” выглядит следующим образом (таблица прилагается).
2.1. Умножение, деление по содержанию и деление на равные части.
На трех первых уроках, специально посвященных умножению. Выясняется смысл понятия умножения как свернутого сложения равных слагаемых (о делении пока не говорится).
Этого времени достаточно для изучения таблицы умножения на 2.
На следующих уроках к каждому из известных случаев умножения приводится соответствующий случай деления. В дальнейшем умножение и деление по содержанию рассматриваются только совместно на одних и тех же уроках.
При введении понятия деления необходимо вспомнить соответствующие случаи умножения, чтобы создать понятие о новом действии. Обратном умножению.
Понятие “умножение” приобретает богатое содержание: оно не только результат сложения равных слагаемых, но и основа, исходный элемент деления, которое представляет свернутое вычитание равных вычитаемых.
Смысл умножения постигается не столько при самом умножении, сколько при постоянных переходах между умножением и делением, ибо деление есть завуалированное, “измененное”, обращенное умножение. Это т объясняет, почему выгодно изучать одновременно умножение и деление.
Пусть нужно по 2 взять 3 раза и 6 разделить по 2.
Дети берут по 2 кружочка и отходят в сторону.
– Эти дети будут составлять задачу.
– По 2 взять один раз, получится 2 (один ученик вкладывает 2 кружочка в наборное полотно),
– По 2 взять 2 раза, получится 4 (аналогично),
– По 2 взять три раза, получится 6.
Запись на доске: по 2 ∙ 3 = 6 (к.)
– Теперь составим обратную задачу. Если в прямой задаче мы собирали кружочки, то в обратной станем раздавать их.
– По сколько кружочков станем раздавать? (По 2.)
– Сколько всего надо раздать? (6.)
– Беру с полотна 2 кружочка, отдаю ученику – 2 кружочка отдали одному человеку (и далее аналогично: по 2 кружочка отдали двум ученикам, по 2 кружочка отдали трем ученикам).
– Сколько всего раздали кружочков?
– Как разделили?
– По сколько делили?
– Скольким ученикам досталось?
На доске запись: 6 : по 2 = 3 (уч.)
| Сравним: | Умножение по 2 ∙ 3 = 6 | Деление 6 : по 2 = 3 |
– Читаем еще раз (с наименованием и без)
– Сравним процесс решения задач:
| – взять столько-то раз (∙) – собираем кружки – нашли (подсчитали, получилось) сколько всего кружков | – разделить по столько-то (:) – раздаем кружки – нашли (подсчитали, получилось) скольким ученикам достались кружки |
На первых уроках по одновременному изучению умножения и деления проводим многократные практические действия по собиранию и раздаче различных предметов. Смысл этих действий показываем в схеме:
Третья операция (деление на равные части) вводится на основе двух ранее известных: умножения и деления по содержанию.
4 ученика принесли по 2 тетради. Сколько всего тетрадей принесли?
– Составьте обратную задачу.
8 тетрадей раздали по 2 тетради. Сколько учеников получат тетради?
– Составьте третью задачу.
8 тетрадей надо раздать поровну четырем ученикам. По сколько тетрадей достанется каждому?
– У меня в руках 8 тетрадей.
– Скольким ученикам надо раздать по 2 тетради? (Вызываю 4-х учеников.)
– Сначала раздаем по одной тетради каждому ученику. Оставшиеся 4 тетради снова раздаем по одной тетради.
– Все тетради раздали?
–По сколько тетрадей получил каждый?
Далее на уроках по изучению умножения и деления широко используем метод решения взаимно обратных задач.
На опытном участке 4 класса посадили по 3 грядки моркови. Сколько всего грядок посадили?
Решение: 3 ∙ 4 = 12 (гр.)
– Сколько данных в задаче?
– Сколько чисел найдено?
– Составьте обратную задачу.
12 грядок моркови посажено несколькими классами. Каждый класс посадил по 3 грядки. Сколько классов участвовало в посадке?
Решение: 12 гр. : по 3 гр. = 4 (кл.)
Даю название вида задач: “умножение”, “деление по содержанию” (таблица прилагается).
– Составьте 2-ую обратную задачу: 12 грядок моркови посажен поровну 4 классами. По сколько грядок посажено каждым 7 классом?
Решение: 12 гр. : 4 = 3 (гр.)
Далее обязательно сравниваем задачи.
2.2. Задачи на увеличение и уменьшение числа в несколько раз и задачи на кратное сравнение величин.
По характеру связей данная тройка задач совершенно аналогична задачам на увеличение и уменьшение числа на несколько единиц и разностное сравнение величин.
Тетрадь стоит 6 рублей, а альбом в 4 раза дороже. Сколько стоит альбом?
– Какова цена тетради?
– Цена альбома?
– Что это значит? (Вместо 1 альбома можно купить 4 т.)
– Как найти стоимость 4 х тетрадей?
– Во сколько раз тетрадь дешевле альбома?
– 24 р. – что означает это число? (Цена альбома.)
– Что надо узнать? (Цену тетради.)
– За что уплатили меньше?
– В предыдущей задаче мы выполнили умножение и нашли цену альбома, так как за него уплатили больше, чем за тетрадь. А за тетрадь уплатили в 4 раза меньше.
– Каким действием найдем цену тетради?
– Сравниваем условия, решения задач. В прямой задаче была дана цена тетради. Что требовалось найти? (Цену альбома.)
– А в обратной задаче? (Наоборот.)
– Какое число входило в условие обеих задач? (В 4 раза.)
– В чем разница между задачами? (В 4 раза дороже – уплатили больше – действие умножения, в 4 раза дешевле – уплатили меньше – действие деления.)
– Какая из задач на увеличение числа, какая – на уменьшение? (Таблица.)
Результатом этого анализа является упрочение в мыслительной практике учащихся двух рядов ассоциаций: дороже в а раз → умножить на а, дешевле в а раз → разделить на а.
Затем применяем обратный переход от задачи на умножение к задаче на увеличение, а от них к понятию “кратное” сравнение.
Изучение темы завершаем упражнениями, когда по одному сюжету и набору чисел составляются все три задачи.
Школьник весит 24 кг, а его ранец с книгами 3 кг. Во сколько раз ученик тяжелее ранца с книгами?
Ранец школьника весит 3 кг, а сам он в 8 раз тяжелее ранца. Сколько килограмм весит школьник?
? кг 3 кг 8 раз
3 ∙ 8 = 24 (кг)
Школьник весит 24 кг, а его ранец в 8 раз легче. Сколько весит ранец?
Далее идет противопоставление задач на разностное и кратное сравнение. Одной из распространенных ошибок учащихся является подмена одного вида сравнения другим.
Чтобы выработать умение различать эти задачи, надо проводить противопоставление задач по трем линиям:
Иногда решаем задачи с несколькими вопросами.
Валя купила 80 см красной ленты и 20 см синей ленты.
– Сколько сантиметров ленты куплено всего?
– На сколько см красная лента длиннее синей?
– Во сколько раз красная лента длиннее синей?
Иногда выполняем структурно противоположное упражнение, когда к условию и данным задачи придумываем вопросы.
Книга стоит 35 р., тетрадь – 5 р. Поставьте вопросы, чтобы первая задача решалась делением, вторая – сложением, третья – вычитанием. После этого решаем задачи на умножение и деление, выраженные в косвенной форме.
2.3. Задачи на нахождение части числа, числа по величине его части. Какую часть составляет одно число от другого?
Естественно, что до введения этих задач дети знакомятся с дробями.
В коробке 32 конфеты. Мама разделила их поровну между четырьмя сыновьями. Какая часть конфет досталась каждому? (Четвертая часть – ¼.)
– Что больше: целая коробка или ее часть?
– Во сколько раз больше?
– Как найти сколько конфет в ¼ коробки?
Обратная задача. В четвертой части коробки 8 конфет. Сколько конфет в целой коробке?
– Где больше конфет: в ¼ или в целой коробке?
– Сколько конфет в целой коробке?
– Сравним условия задач и процессы их решения.
– Какие числа были даны в прямой задаче?
– Что они обозначают?
– А в обратной?
– Скажите вопросы прямой и обратной задач.
– Какими действиями решали задачи?
На следующих уроках выполняем обратные преобразования. После этого вводится третья задача этого цикла.
Купили несколько груш. Третья часть груш составляет 7 груш. Сколько всего было груш?
Обратная задача. Купили 21 грушу. Сколько груш составляет 1/3 часть?
Обратная задача. Какую часть составляет 7 яблок от 21 яблока?
– Во сколько раз 21>7?
– Как это найти? 21 : 7 = 3 (раза)
– Какую часть составляет 7 яблок от 21 яблока? (Третью.)
Затем выполняются закрепительные упражнения по решению задач на умножение и деление.
Конспект внеклассного занятия по математике для 3 класса на тему «Обратные задачи»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Конспект внеклассного занятия по математике в 3 классе на тему: «Обратные задачи»
Сегодня на занятии мы с вами продолжим знакомиться с загадочным и интересным миром занимательной математики. Но для начала я хочу посмотреть с каким настроением вы пришли. Покажите это при помощи сигнальных карточек.( красный-настроение отличное,к уроку готов, желтый-еще не решил,но буду стараться, зеленый-переживаю,сомневаюсь в своих знаниях).
Ученик зачитывает девиз занятия:
Чтоб водить корабли,
Чтобы летчик стать,
Уметь задачи решать.
Ведь на свете нет профессии пока,
Где бы нам не пригодилась математика.
Ребята, как вы понимаете этот девиз?( в любой профессии нужна математика, чтоб все получалось,нужно преодолевать различные трудности)
Так давайте прямо сейчас начнем преодолевать трудности. Посмотрите на экран, разгадайте ребусы (дети решают ребусы). А сейчас посмотрите на следующее задание, сколько прямоугольников вы видите на экране?( на экране квадрат,разбитый на несколько прямоугольников. Дети считают их количество ).
Не будет в математике удачи,
Коль не подружишься с задачей.
Друзья, что вы знаете о задачах ?(задачи люди начали решать очень давно. Задачи используются в разных случаях, например, при строительстве домов или при совершении покупок)
Назовите основные части задачи.( условие, вопрос,решение,ответ )
А какие виды задач вам известны?( задачи-загадки,задачи-шутки,логические задачи,задачи на смекалку, обратные задачи, задачи с геометрическим содержанием… )
Одна нога и шапка,а головы нет .(гриб)
Кто становится выше,когда садится?( собака)
Сколько ног у жука ?(6)
Сколько ног у паука?( 8)
Ребята,а к какому виду животных относятся жуки ?(насекомые)
А к какому виду животных относятся пауки?( пауки)
Давайте посмотрим как вы справитесь со следующими задачами.
Чему равен периметр треугольника со сторонами 10 см,15 см,18 см и 42 см? ( нет такого треугольника )
Шла Баба в Москву и повстречала трех мужиков. Каждый из них нес по мешку, в каждом мешке по коту. Сколько существ направлялось в Москву?( одна Баба )
Три юные утки в оранжевых шляпках,
Три юные мышки в беретах и тапках,
Три юные кошки с вуалью на лицах,
И три собачонки в рубашках их ситца,
А также три юные толстые свинки
Решили до речки дойти по тропинке.
Но к вечеру дождик полил проливной,
И всем им пришлось возвратиться домой.
Сколько всего было туристов?( 15)
Друзья, существует огромное количество различных задач. Напомните, с какими задачами мы работали на прошлом занятии?( с обратными )
Что такое обратные задачи ?(задачи, в которых известное становится неизвестным, а неизвестное-известным)
Правильно, и сегодня мы продолжим работать по этой теме.
Поставьте перед собою цель.
Предлагается слайд с задачами:
1.На землю с деревьев упало 15 дубовых и 16 кленовых
листочков.Сколько всего на земле листочков?
2. В лесу листопад. На землю с деревьев упал 31 листочек.
Кленовых было 16. Сколько на земле дубовых листочков?
3. В лесу листопад. На землю с деревьев упал 31 листочек. Из
них было 15 дубовых. Сколько на земле кленовых листочков?
Посмотрите на данные задачи. Одинаковы ли они?( нет ).
В чем сходство?( схожи числа и данные )
О чем говорится в задачах? ( о кленовых и дубовых листочках, о том, что они упали на землю )
В чем различие?( вопросы отличаются )
У каждого на столе лежит карточка (Приложение 1)
Заполните самостоятельно карточки, внимательно ознакомьтесь с условием задач, решите эти задачи.( дети самостоятельно заполняют пропуски на карточках )
Поменяйтесь карточками и проверьте друг друга.
Как можно назвать вторую и третью задачу? ( обратная первой )
В какой форме мы записали условие задач?( краткой записи )
Как еще можно оформить эти задачи?( при помощи схематичного рисунка )
Ученик демонстрирует у доски схематическую запись задачи.
На разминку становись.
Раз,два,три, не отставай.( повороты туловищем вправо,влево )
Раз, два, три, четыре, пять.
Тот,кто делает зарядку
Может на сплясать вприсядку.( приседания )
А теперь поднимем ручки
И опустим их рывком.
А теперь ходьба на месте,
Левой, правой, стой, раз-два( ходьба на месте )
Мы за парты сядем вместе.
Вновь возьмемся за дела.
Теперь давайте поработаем в группах.
Сейчас каждой группе я раздам по три карточки .( Приложение 2 )
Выберете только те карточки, в которых вы видите прямую задачу и две обратные ей.( дети работают в группах )
Ребята, зачем мы выполняли сейчас это задание?( чтобы уметь отличать обратную задачу от прямой ). Правильно.
А теперь вновь посмотрите на экран. Прочитайте задачу.
Карандаш стоит 12 рублей, а тетрадь 48 рублей. Сколько стоит вся покупка?
Задание для первой группы: составьте обратную задачу, где неизвестна стоимость карандаша.
Задание для второй группы: составьте обратную задачу, где неизвестна стоимость тетради.
( дети работают в группах ).
Первая группа, зачитайте свою задачу. Вторая группа, решите ее.( ученик из первой группы читает задачу, ученик из второй группы решает ее у доски ).
Теперь послушаем что поучилось у второй группы. Первая группа, решите задачу.( ученик из второй группы читает задачу, ученик из первой группы решает ее у доски. )
Ребята, а с какой целью вы выполняли данное задание?( закрепить умение составлять и решать обратные задачи )
На слайде две задачи:
1. В буфет завезли 3 ящика с печеньем,каждый из них весит по 6 кг. Сколько кг печенья завезли в буфет?
2. Маша собрала 8 сыроежек, а подберезовиков в 3 раза больше. Сколько подберезовиков собрала Маша?
Посмотрите на экран. Перед вами две задачи. Первый вариант составляет обратную задачу к первой, а второй вариант составляет задачу, обратную второй.
Ребята, чему вы сегодня научились?
Какие задачи называются обратными?
Какие цели вы ставили перед собой?
Кто сегодня на занятии испытывал трудности?
Что нужно сделать, чтобы их устранить?
Кому было легко сегодня решать задачи?
Оцените свою работу при помощи сигнальных карточек( красный-отлично!было интересно! Желтый-я старался, и все получилось, зеленый-нужно повторить материал. )
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-350407
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителям истории предлагают предоставить право бесплатно посещать музеи
Время чтения: 2 минуты
Во Франции планируют ввести уголовное наказание за буллинг в школе
Время чтения: 1 минута
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Школьники из Москвы выступят на Международной олимпиаде мегаполисов
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.