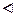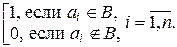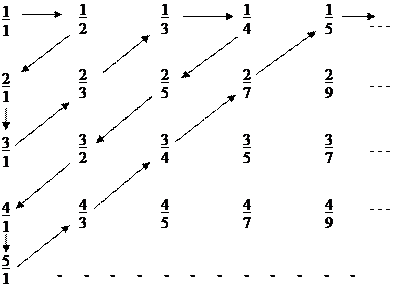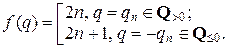Что такое взаимно однозначное соответствие между множествами
Математика
Множества и операции. Понятие множества.
Взаимно однозначное соответствие между двумя множествами
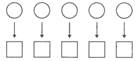
Разложим наши яблоки, хотя бы на столе, и попробуем положить против каждого яблока пр груше. Возможны три случая (рис. 2).
Первый случай: против каждого яблока окажется груша, и при этом не только все яблоки, но и все груши окажутся разложенными. В этом случае, очевидно, у нас столько же яблок, сколько и груш.
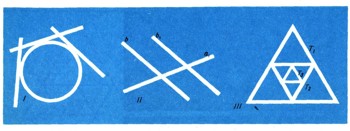
В математике можно найти многочисленные примеры взаимно однозначных соответствий. Например, каждой вершине треугольника или тетраэдра соответствует противоположная этой вершине сторона или грань. Таким образом, установлено взаимно однозначное соответствие между множеством всех вершин треугольника (тетраэдра) и множеством всех его сторон (граней). Множество всех сторон правильного многоугольника находится во взаимно однозначном соответствии с множеством всех перпендикуляров, которые опущены на эти стороны из центра правильного многоугольника. Множество всех боковых граней пирамиды находится во взаимно однозначном соответствии с множеством апофем этой пирамиды и т. д.
Да, есть и такой музей. Часов там много всяких: старинных и современных, механических и электрических, огромных и крошечных, с боем и без боя, с циферблатом и без циферблата.
Ответы и решения
Ответ. 1000000000=10 9 =(2*5) 9 =2 9 *5 9 = 51,2*1953126. 1 000 000 000 000 000 000 = 10 18 = 2 18 * 5 18 = 262 144 * 3 814 697 265 625. каждый из которых, кроме первого, вписан в предыдущий (рис. 3, III). Множество всех этих треугольников обозначим через X. Каждый треугольник получил определенное натуральное число п в качестве своего номера.
Номером треугольника Тn является натуральное число п. Этим, очевидно, установлено взаимно однозначное соответствие между множеством X наших треугольников и множеством всех натуральных чисел.
Понятие соответствия между множествами



Соответствием между элементами множества Х и элементами множества Y называется любое подмножество декартова произведения этих множеств.
Взаимно однозначные соответствия.
Взаимно однозначным соответствием между множествами X и Y называется такое соответствие, при котором каждому элементу множества X сопоставляется единственный элемент множества Y и каждый элемент множества Y соответствует только одному элементу множества X.
Если множества конечны, то отношение взаимно-однозначно только, если они содержат одинаковое количество элементов.
Если между множествами можно установить взаимно-однозначное соответствие, то такие множества называются равномощными.
Объединение, пересечение и вычитание множеств. Свойства объединения и пересечения (с иллюстрацией на кругах Эйлера). Примеры заданий из начального курса математики, при выполнении которых учащиеся явно (или неявно) выполняют объединение (пересечение, вычитание ) множеств.
Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В. Объединение множеств А и В обозначают А ÈВ. Таким образом, по определению, А ÈВ = <х \ х ÎА или х Î В].


Примеры:


Если изобразить множества А и В при помощи кругов Эйлера, то пересечением данных множеств является заштрихованная область. В случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто и пишут: А ÇВ =Æ.
Эквивалентные множества
Мощность конечного множества
Мощностью конечного множества называют число элементов этого множества.
В общем случае мощность множества A обозначают |A|.
Для конечных множеств чаще встречается обозначение n(A).
Конечные множества легко сравнивать по мощности.
Если n(A) = n(B), то конечные множества A и B равномощны.
Например: Мощность множества A= <1;3;5;7>равна n(A)=4.
Мощность множества B = <-3;13;2;4>равна n(B) = 4.
Множества A и B равномощны.
Взаимно однозначное соответствие двух множеств
1) каждому элементу множества A соответствует только один элемент множества B;
2) каждый элемент множества B при этом соответствует некоторому элементу множества A;
3) разным элементам множества A соответствуют разные элементы множества B.
Каждый раз, когда мы «считаем» множество каких-то объектов, мы устанавливаем взаимно однозначно соответствие между этим множеством и подмножеством натуральных чисел от 1 до некоторого n.
С этой точки зрения утверждение
«У Толи три друга: Вася, Коля и Петя» выглядит как соответствие:
Эквивалентность
Такой подход даёт нам возможность сравнивать по мощности не только конечные, но и бесконечные (!) множества.
Сравним мощности множеств натуральных и натуральных чётных чисел:
Для мощности натуральных чисел используется специальное обозначение:
Счётные и несчётные множества
Чтобы доказать счётность множества достаточно придумать правило, по которому нумеруются его элементы.
Докажем, что множество целых чисел счётно.
Что и требовалось доказать.
Таким образом, множество отрезка [0;1]оказывается мощнее всего множества натуральных чисел.
Любой отрезок [a;b] и отрезок [0;1] эквивалентны.
Мощность любого действительного отрезка равна мощности континуума.
Чтобы доказать несчётность множества, нужно показать, что нет таких правил, по которым можно его посчитать. Это значительно сложнее, чем доказать счётность.
Примеры
Пример 1. Среди данных конечных множеств укажите пары эквивалентных:
Запишем с помощью перечисления:
$A \sim B, B \sim C, A \sim C$
В каждый треугольник можно вписать окружность, и притом только одну. Условие единственности (1) выполняется.
Вокруг каждой окружности можно описать бесконечное количество правильных треугольников, поворачивая их на некоторый угол относительно центра окружности.
Условие (2) не выполняется.
Соответствие не является взаимно однозначным.
Пример 3. Постройте взаимно однозначное соответствие между отрезком [0;1] и отрезком [2;7] с помощью линейной функции.
Искомая функция имеет вид y = kx+b, где
Прямая проходит через две точки: A(0;2),B(1;7).
Прямая проходит через две точки: A(0;a),B(1;b). Уравнение прямой:
ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ
Смотреть что такое «ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ» в других словарях:
ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — такое соответствие между элементами двух множеств, при котором каждому элементу первого множества соответствует один определенный элемент второго множества, а каждому элементу второго множества один определенный элемент первого множества … Большой Энциклопедический словарь
взаимно однозначное соответствие — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN bijection … Справочник технического переводчика
взаимно-однозначное соответствие — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN one one mappingone to one correspondenceone to one dependence … Справочник технического переводчика
взаимно однозначное соответствие — такое соответствие между элементами двух множеств, при котором каждому элементу первого множества соответствует один определённый элемент второго множества, а каждому элементу второго множества один определённый элемент первого множества. * * *… … Энциклопедический словарь
ВЗАИМНО-ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — [или одно однозначное; сокращенно: (1–1) – соответствие] – одно из основных понятий теорий множеств (см. Множеств теория); частный случай понятия функции. Два множества A и B находятся в отношении В. о. с, если каждому элементу множества А… … Философская энциклопедия
взаимно однозначное соответствие — ▲ соответствие (между) ↑ взаимно, определенный ▼ отпечаток (рельефа), подобный … Идеографический словарь русского языка
Взаимно однозначное соответствие — (математическое) такое соответствие между элементами двух множеств, при котором каждому элементу первого множества соответствует один определённый элемент второго множества, а каждому элементу второго множества один определённый элемент… … Большая советская энциклопедия
Взаимно однозначное соответствие — Биективная функция. Функция называется биекцией (и обозначается ), если она: Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами … Википедия
ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — такое соответствие между элементами двух множеств, при к ром каждому элементу первого множества соответствует один определ. элемент второго множества, а каждому элементу второго множества один определ. элемент первого множества … Естествознание. Энциклопедический словарь
взаимно-однозначное отображение — взаимно однозначное соответствие — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы взаимно однозначное соответствие EN one to one mapping … Справочник технического переводчика
Взаимно однозначное соответствие. Мощность множества. Счетные, несчетные, континуальные множества и их свойства
Иногда бывает необходимо сопоставлять друг с другом элементы некоторых множеств. Рассмотрим, например, два множества: стадо из четырехсот овец и рощу из четырехсот деревьев. Эти множества можно попарно сопоставить друг с другом, привязав овец к деревьям, так что каждая овца и каждое дерево будут в точности принадлежать одной определенной паре. Ни одно из данных множеств не может быть по такому принципу попарно сопоставлено, например, с рощей из семисот деревьев или с множеством из трехсот камней.
Для взаимно однозначного соответствия можно дать следующее определение.
Определение 2.2.1. Взаимно однозначным соответствием между двумя непустыми множествами А и В называется такое правило (или закон) f, по которому каждому элементу а Î А ставится в соответствие единственный элемент f(а) Î В и для любого элемента b Î В существует единственный элемент а Î А, такой что f(а) = b, другими словами, f задает биекцию между А и В.
Определение 2.2.2. Множества А и В называются равномощными (обозначение А « В), если между ними можно установить взаимно однозначное соответствие.
Очевидно, что если множество А равномощно В, а В равномощно С, то А равномощно С, то есть А « В & В « С Þ А « С – свойство транзитивности.
Определение 2.2.3. Число элементов в конечном множестве А называется мощностью А и часто обозначается | А |. Пустое множество, то есть не содержащее элементов, относят к конечным, оно является множеством мощности 0: | Æ | = 0.
Мощность бесконечного множества – более сложное понятие. Оно будет рассмотрено ниже.
Теорема 2.2.1. Между непустыми конечными множествами А и В существует взаимно однозначное соответствие тогда и только тогда, когда | А | = | В |.
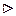
Достаточность. Пусть | А | = | В | = n Î N. Тогда А = <а1, а2,…, аn>, В = <b1, b2,…, bn>. Рассмотрим правило f, по которому каждому элементу аi Î А ставится в соответствие единственный элемент bi Î B. Тогда для » bi Î B существует единственный элемент ai Î A, такой что f(ai) = bi. Значит, f задает взаимно однозначное соответствие между множествами А и В.
В связи с этой теоремой становится понятно, почему два первых множества из примера в начале параграфа находятся во взаимно однозначном соответствии друг с другом, но не являются равномощными третьему и четвертому множествам. Сколько же существует таких взаимно однозначных соответствий для двух n-элементных множеств А и В?
Теорема 2.2.2. Общее число взаимно однозначных соответствий для двух n-элементных множеств равно n!.
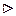
n × (n – 1) × (n – 2) ×…× 2 × 1 = n!.
Теорема 2.2.3. Пусть А1,…, Аn – конечные множества и | Ai | = mi, 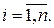
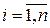
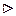
Если Ai = А, 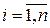
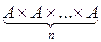
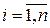
Следствие.| A n | = | A | n для любого n Î N.
Теорема 2.2.3 и следствие из нее лежат в основе очень многих комбинаторных фактов.
Определение 2.2.4. Пусть А – некоторое множество. Множеством-степенью или булеаном множества А называется множество Р(А) = <Х | Х Í A> – множество всех подмножеств множества А.
Вернемся к теореме 2.2.1. Во-первых, она позволяет установить равенство мощностей двух конечных множеств, не вычисляя этих мощностей, а во-вторых, часто дает возможность вычислить мощность множества, установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется. В качестве иллюстрации этого приема докажем важную теорему о числе подмножеств конечного множества.
Пусть n Î N. Рассмотрим множество Вn всех двоичных слов (векторов) из нулей и единиц длиной n. Каждому подмножеству В Í А сопоставим двоичное слово SB длиной n, построенное по следующему правилу:
SB = (a1,…, an), где ai =
Пусть требуется определить число всех k-элементных подмножеств n-элементного множества А, n Î Z³0. Очевидно, что k должно удовлетворять неравенству: 0 £ k £ n. Если А = Æ, то n = k = 0 и число 0-элементных подмножеств равно | P(Æ) | = 1. Пусть теперь n Î N. Поскольку, как уже было сказано в доказательстве теоремы 2.2.4, множества Р(А) и Вn равномощны, то число всех k-элементных подмножеств в А равно числу всех двоичных слов длиной n, в которых k символов равны 1, а остальные равны 0. Это число равно числу сочетаний из n элементов по k: 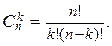
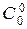
Если множества являются бесконечными, то установление между ними взаимно однозначного соответствия наталкивается на трудности, связанные с необходимостью оперировать с бесконечно большим числом элементов множества. За основу для сопоставления бесконечных множеств принято брать натуральный ряд чисел N: 1, 2, 3,…, n,…
Определение 2.2.5. Множество, равномощное множеству натуральных чисел N, называется счетным.
Вообще любое бесконечное подмножество множества N счетно. Действительно, пусть 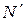
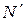
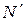
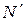
Таблица 2.2.1
Обходя таблицу 2.2.1 по направлению стрелок, начиная от 1/1 = 1, приходим к последовательности 1, 1/2, 2, 3, 2/3, 1/3, 1/4, 2/5, 3/2, 4, 5, 4/3, 3/4, 2/7, 1/5,…, позволяющей занумеровать все эти числа. Обход таблицы можно осуществить и другими способами, например, по «квадратам». Итак, задано правило, по которому каждому числу q Î Q>0 ставится в соответствие единственное число n Î N, являющееся номером q в данной последовательности. И для любого числа n Î N существует единственное число q Î Q>0 такое, что q имеет номер n в данной последовательности. Итак, Q>0 равномощно N.
Теперь рассмотрим множество всех рациональных чисел Q. Было показано выше, что Q>0 = <q1, q2, q3,…, qm,…> = <qi | i Î N>. Обозначим теперь q0 число 0. Построим взаимно однозначное соответствие f : Q ® N следующим образом, как показано на рис. 2.2.2.
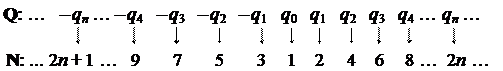 |
Рис. 2.2.2
Из приведенных примеров видно одно из замечательных свойств бесконечных множеств, которое не имеет места в случае конечных множеств, – возможность приведения во взаимно однозначное соответствие бесконечного множества с его же бесконечным подмножеством.
Объединение конечного числа счетных множеств A1, A2,…, Ak, k Î N,счетно. Действительно, перенумеруем сначала все первые элементы множеств, затем вторые и т.д. Объединение счетного множества конечных множеств также счетно (сначала нумеруем все элементы первого множества, затем все элементы второго множества и т.д.). Из последнего утверждения следует, что множество всех слов в любом конечном алфавите счетно. Менее очевидно, что счетно и объединение счетного множества счетных множеств. Примером такого объединения является множество 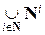
Определение 2.2.6. Если бесконечное множество не равномощно множеству N, то такое множество называется несчетным.
Существование несчетных множеств следует из теоремы, доказанной в 1874 г. известным немецким математиком Георгом Кантором (1845–1918).
Теорема 2.2.5 (Г. Кантор). Множество всех действительных чисел интервала (0; 1) несчетно.
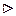
Рассмотрим любую бесконечную десятичную дробь 0,b1b2b3… такую, что b1 ¹ a11, b2 ¹ a22, b3 ¹ a33 и т.д. Эта дробь не может войти в указанную последовательность, так как от первого числа она отличается первой цифрой, от второго числа – второй цифрой и т.д. Следовательно, все вещественные числа интервала (0; 1) не могут быть пронумерованы и данное множество несчетно.
Определение 2.2.7. Мощность множества всех действительных чисел интервала (0; 1) называется континуум, множества такой мощности называются континуальными. Метод, использованный при доказательстве теоремы 2.2.5, называется диагональным методом Кантора.
Необычные свойства несчетных множеств проявляются в том, что рассмотренный интервал (0; 1) может быть приведен во взаимно однозначное соответствие с полуинтервалами [0; 1) (рис. 2.2.3), (0; 1], отрезком [0; 1], а также множествами (a; b), (a; b], [a; b), [a; b], где a, b Î R, a 2 « R и вообще R n « R для любого n Î N.
Множество всех подмножеств счетного множества континуально. Это становится ясным, если воспользоваться, как и в теореме 2.2.4, представлением подмножества в виде последовательности (но теперь уже бесконечной!) нулей и единиц: на i-ом месте стоит 1, если i-й элемент множества входит в данное подмножество, и 0 в противном случае. Получаем взаимно однозначное соответствие между собственными подмножествами счетного множества и правильными двоичными дробями, все множество которых, в свою очередь, взаимно однозначно соответствует множеству всех вещественных чисел полуинтервала [0; 1). Как показывается в теории множеств (с помощью метода, аналогичного диагональному методу Кантора), для множества любой мощности его булеан имеет более высокую мощность. Поэтому не существует множества максимальной мощности. Хорошо известным в истории математики является парадокс Кантора «Множество всех множеств». По смыслу своего описания оно должно содержать все мыслимые множества и, следовательно, иметь максимальную мощность, что противоречит результатам теории множеств. Однако само это «множество всех множеств» содержится в своем булеане в качестве элемента и поэтому не может иметь максимальную мощность. И, таким образом, кажущееся противоречие разрешается.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет