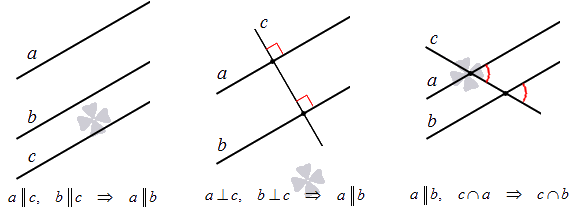Что такое взаимное расположение прямых в геометрии

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

Источник

Прямая на плоскости – необходимые сведения

Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.

Прямая на плоскости – понятие

Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.

Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.

Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Взаимное расположение прямой и точки

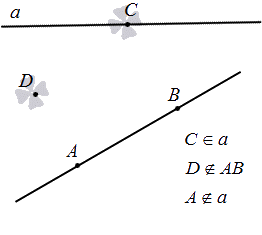
На каждой прямой и в каждой плоскости могут быть отмечены точки.

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Точка делит прямую на две части, называемые лучами. Имеем аксиому:

Взаимное расположение прямых на плоскости

Расположение прямых на плоскости может принимать вид двух состояний.

Две прямые на плоскости могут совпадать.

Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.

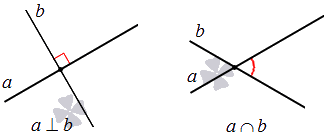
Две прямые на плоскости могут пересекаться.

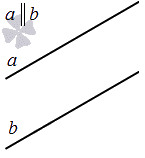
Две прямые на плоскости могут быть параллельны.

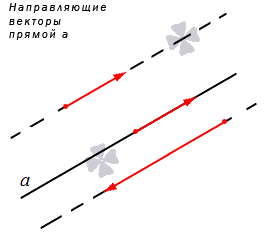
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.

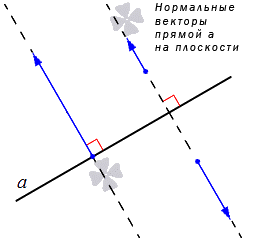
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.

Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.

Для этого приводим необходимы факторы, доказывающие их взаимное расположение:

Рассмотрим это на рисунках.

Способы задания прямой на плоскости

Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.

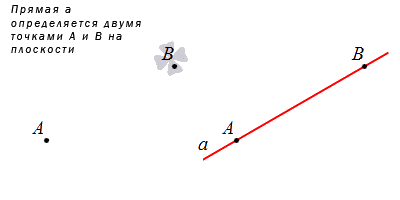
Прямая задается при помощи указанных двух точек, расположенных в плоскости.

Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.

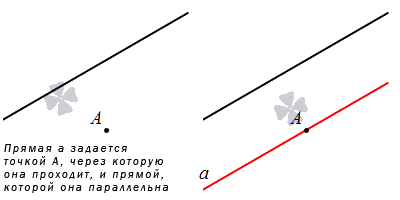
Прямая может быть задана через точку и прямую, которой она параллельна.

Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.

Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.

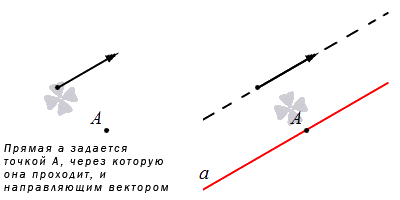
Прямая задается через указанную точку и направляющий вектор.

Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.

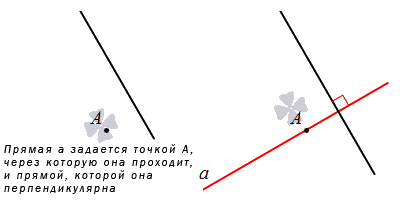
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:

Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.

И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.

Источник

Геометрия. 10 класс

Взаимное расположение прямых в пространстве

Взаимное расположение прямых в пространстве

Взаимное расположение прямых в пространстве

Угол между прямыми в пространстве

Взаимное расположение прямых в пространстве: скрещивающиеся прямые

Необходимо запомнить

Определение. Скрещивающиеся прямые – прямые, которые не лежат в одной плоскости.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Теорема. Если стороны двух углов соответственно сонаправлены, то такие углы равны.

Взаимное расположение прямых в пространстве

Теорема. Если стороны двух углов соответственно сонаправлены, то такие углы равны.

При доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

1. Стороны углов сонаправлены, а значит, параллельны. Проведем через них плоскости, как показано на чертеже.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырёхугольника равны и параллельны по условию, то этот четырёхугольник – параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны и параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁ || BB₁ и AA₁ = BB₁.

По определению четырёхугольник АВВ₁А₁ – параллелограмм, из этого получаем АВ = А₁В₁.

5. Из выше построенного и доказанного АВ = А₁В₁, ОA = O₁A₁ и OB = O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трём сторонам, и поэтому О = О₁.

Источник

Взаимное расположение прямых в пространстве

Возможны четыре различных случая расположения двух прямых в пространстве:

– прямые скрещивающиеся, т.е. не лежат в одной плоскости;

– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;

– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;

Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями

где — точки, принадлежащие прямым и соответственно, a — направляющие векторы (рис.4.34). Обозначим через вектор, соединяющий заданные точки.

Перечисленным выше случаям взаимного расположения прямых и соответствуют следующие признаки:

– прямые и скрещивающиеся векторы не компланарны;

– прямые и пересекаются векторы компланарны, а векторы не коллинеарны;

– прямые и параллельные векторы коллинеарны, а векторы не коллинеарны;

– прямые и совпадают векторы коллинеарны.

Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:

Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности. Поэтому:

– прямые и скрещивающиеся определитель отличен от нуля;

– прямые и пересекаются определитель равен нулю, а вторая и третья его строки не пропорциональны, т.е.

– прямые и параллельные вторая и третья строки определителя пропорциональны, т.е. а первые две строки не пропорциональны, т.е.

– прямые и совпадают все строки определителя пропорциональны, т.е.

Расстояние между параллельными прямыми

Найдем расстояние между параллельными прямыми, заданными каноническими уравнениями (рис.4.35)

где — произвольные точки на прямых и соответственно, а координаты направляющих векторов прямых пропорциональны:

Расстояние между скрещивающимися прямыми

Напомним, что расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра, т.е. кратчайшее расстояние между точками этих прямых.

Найдем расстояние между скрещивающимися прямыми, заданными каноническими уравнениями

где — произвольные точки на прямых и соответственно.

Искомое расстояние равно высоте параллелепипеда, построенного на векторах (рис.4.36), т.е.

— смешанное и векторное произведения векторов. Как показано выше, прямые и скрещивающиеся тогда и только тогда, когда векторы некомпланарные, т.е.

Отсюда следует, что вторая и третья строки не пропорциональны. Поэтому векторы неколлинеарные, т.е. и знаменатель в правой части (4.38) отличен от нуля.

Угол между прямыми

Угол между прямыми определяется как угол между их направляющими векторами. Поэтому величина острого угла между прямыми

вычисляется по формуле

Решение. Каноническое уравнение оси абсцисс имеет вид так как ось проходит через точку а — ее направляющий вектор. Каноническое уравнение прямой получено в примере 4.15,»а»:

Полагая по формуле (4.38) получаем:

Острый угол находим по формуле (4.39):

Взаимное расположение прямой и плоскости

Возможны три случая взаимного расположения прямой и плоскости:

– прямая и плоскость пересекаются, т.е. имеют одну общую точку;

– прямая и плоскость параллельны, т.е. не имеют общих точек;

– прямая лежит в плоскости, т.е. все точки прямой принадлежат плоскости.

Получим признаки для всех этих случаев. Пусть прямая и плоскость заданы уравнениями:

т.е. прямая проходит через точку коллинеарно вектору а плоскость перпендикулярна вектору

Перечисленным выше случаям взаимного расположения прямой и плоскости соответствуют следующие признаки:

– прямая и плоскость пересекаются векторы и не ортогональны (рис.4.37,а);

– прямая и плоскость параллельны векторы и ортогональны, а точка не принадлежит плоскости (рис.4.37,б);

– прямая лежит в плоскости векторы и ортогональны, а точка принадлежит плоскости (рис.4.37,в).

Учитывая свойство скалярного произведения векторов получаем:

– прямая и плоскость пересекаются ;

– прямая и плоскость параллельны

– прямая лежит в плоскости

Угол между прямой и плоскостью

Отсюда, например, следует полученное ранее необходимое условие параллельности прямой и плоскости.

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

3.4. Взаимное положение прямых

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.

1. Пересекающиеся прямые

Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.

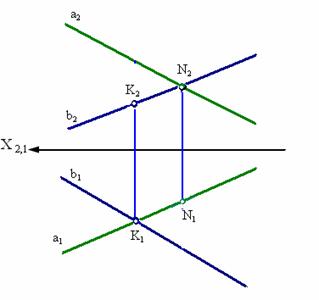
Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).

.

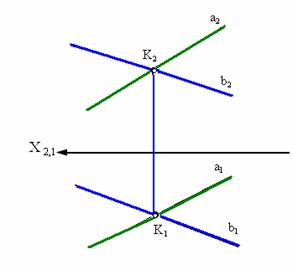
Рис. 3.4. Пересекающиеся прямые

2. Параллельные прямые

На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).

Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.

Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.

На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).

.

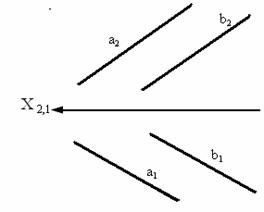
Рис. 3.5. Изображение параллельных прямых

.

Источник