Что такое взвешенные графы
Погружение в графы
Графы в большинстве своем представляют собой неупорядоченные деревья. В основном это утверждение касается ненаправленных и невзвешенных графов. Однако оно остается в силе и в отношении направленных или взвешенных графов, либо направленных и взвешенных одновременно, только при этом надо детализировать понятие “неупорядоченности”.
Направленные графы
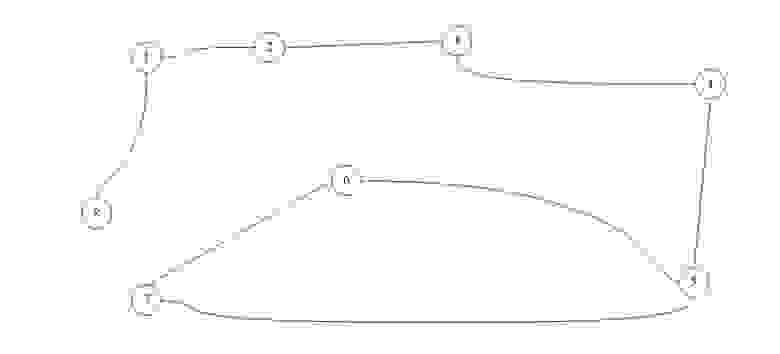
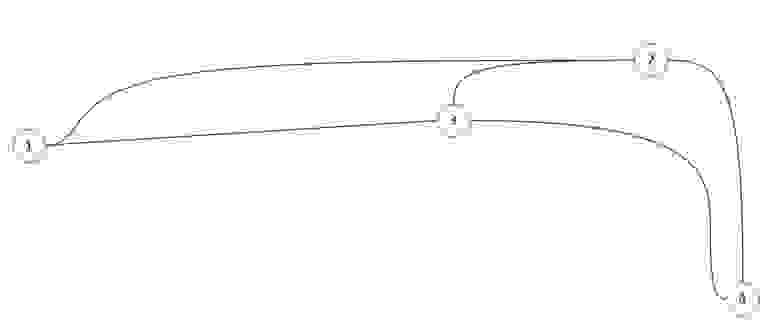
Прежде, чем познакомиться с направленным графом, взгляните на ненаправленный граф, представленный ниже:
Ненаправленный граф позволяет свободно перемещаться между вершинами в любом направлении. Теперь посмотрите на направленную версию этого графа:
Тут все меняется. Вы можете перемещаться между вершинами только в направлении стрелки, прикрепленной к каждому ребру. Например, вы можете перейти из пункта А в пункт В, но не из пункта В в пункт А. Немного более строго, верно?
Взвешенные графы
Теперь подумаем о том, чтобы добавить веса ребрам графа. Представьте себе, что у каждого ребра есть цена; цена, которую нужно заплатить, чтобы пересечь ребро. Но перед этим представьте, что все ребра бесплатные, то есть имеют нулевую цену.
На самом деле это мало что меняет, так как с самого начала не было никакой цены, которую нужно было платить. Мы все еще можем пройти по графу без раздумий, если будем следовать указаниям стрелок. Даже если у каждого ребра есть цена, пока все они равны, поскольку каждое ребро имеет одинаковое значение, или вес.
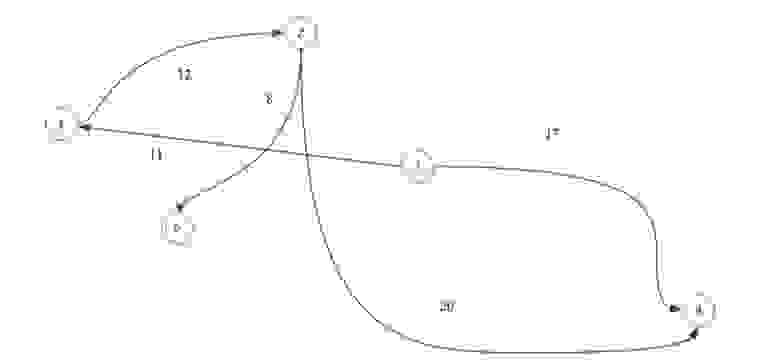
Хорошо, но что, если бы цены были другими? Как бы это изменило способ прохождения по графу?
Поскольку цены теперь отличаются друг от друга, вводится новая динамика. Переход от вершины к вершине будет стоить разных сумм “денег”. Иногда есть только один путь, но в некоторых случаях можно выбрать маршрут, и цена обычно служит определяющим фактором в этом решении. В общем, при переходе из одной вершины графа в другую “самый дешевый” путь является желаемым. Например, если бы я хотел выбрать самый дешевый путь из пункта А в пункт Е, я бы пошел по маршруту АBDЕ. Хотя первоначальным решением мог бы стать маршрут ABE, на самом деле он вышел бы дороже. Подсчеты показывают: стоимость ABE составляет 11, в то время как АBDЕ — всего 9. Надеюсь, вы получили основное представление о взвешенных графах.
До этого момента я называл числа, представляющие каждое ребро, его “ценой”, имея в виду деньги. На самом деле эти цифры обозначают “вес” ребра. Аналогия с деньгами упрощает знакомство с этим видом графа, поскольку деньги — это то, с чем все мы знакомы. Есть и другие способы рассмотрения взвешенного графа. Вы можете представить числа как расстояние между двумя вершинами. Большинство иллюстраций графов не соотнеслись бы с таким представлением, но, тем не менее, такая аналогия тоже приемлема.
Представление графов в коде
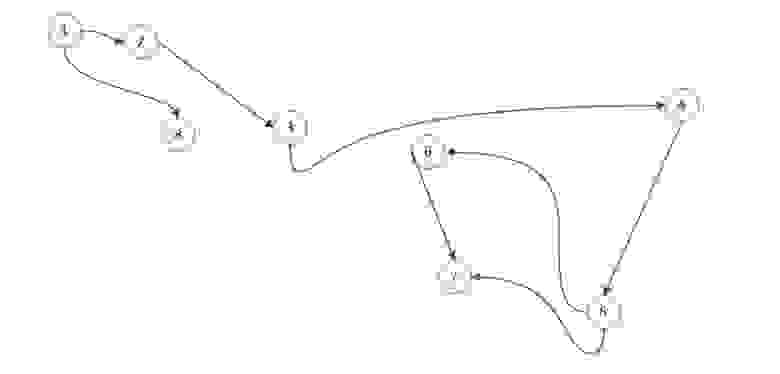
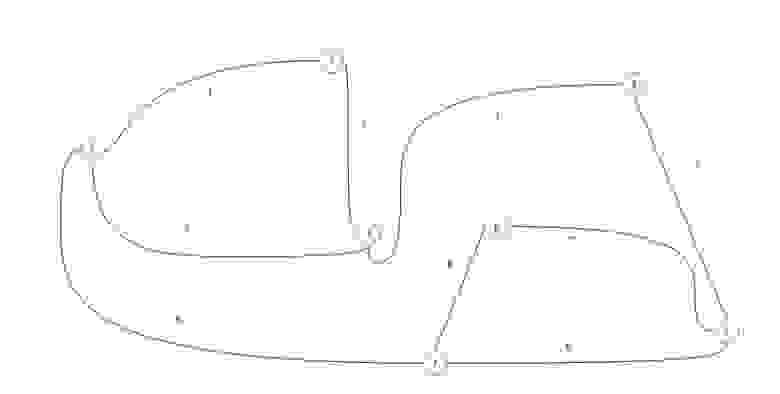
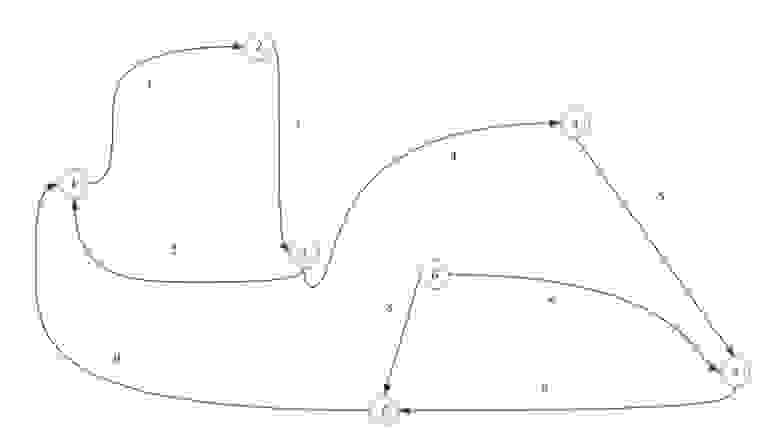
Итак, вы уже знаете, что такое направленные и взвешенные графы. Теперь выясним, как представить графы в коде. До сих пор мы использовали только иллюстрации графов. Что ж, оказывается, существует множество способов их представления в коде. Рассмотрим некоторые из них в отношении направленного и невзвешенного графа, показанного ранее.
Список ребер
Список ребер — это именно то, на что похож приведенный ниже код; это список всех ребер на графе. Обратите внимание: каждое ребро представлено своими вершинами — начальной и конечной.
Список смежности
Список смежности — это что-то вроде словаря, в котором каждый ключ является вершиной в графе, а каждое значение — это все, к чему эта вершина примыкает. В направленном графе стрелки должны быть направлены так, чтобы вершина была ключом в списке.
Матрица смежности
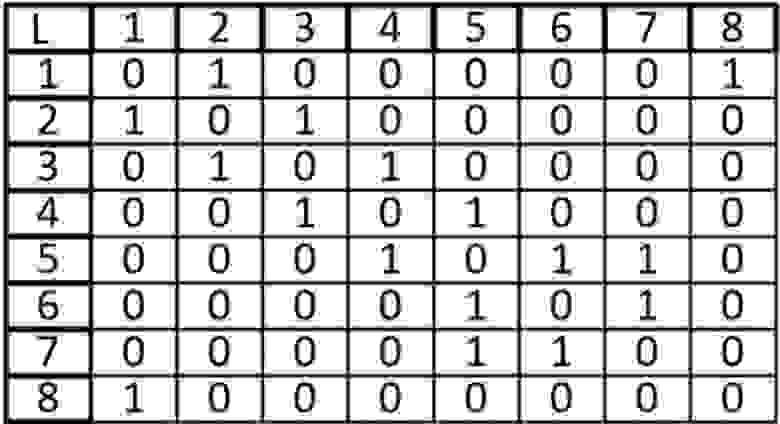
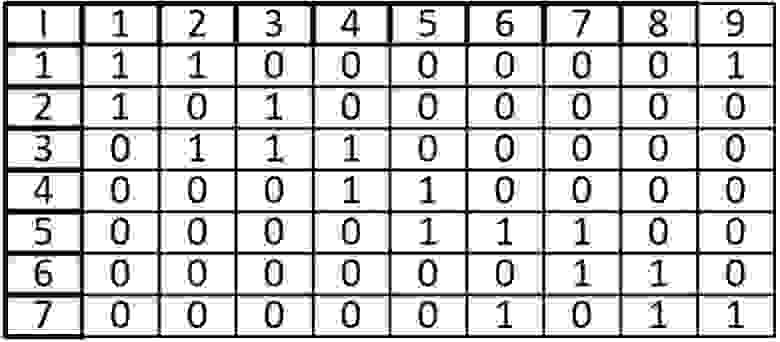
Чтобы лучше понять матрицу смежности, изобразим ее в виде рисунка. Если у вас есть опыт работы с матрицами в исчислении, то вам это дастся довольно легко. Если нет, не стоит беспокоиться — всему свое время.
В матрице смежности “0” означает, что две вершины не являются смежными, а “1”, указывает на то, что они являются смежными. Существует множество способов манипулировать такой матрицей и работать с ней, но это выходит за рамки данного объяснения. Обратите внимание на то, что на диагонали есть только нули. Подумайте, почему это так…
Для кодирования матрицы смежности существует несколько способов. В следующих случаях используется ООП:
Когда следует использовать каждый метод
Каждый метод является допустимым представлением графа. Когда же предпочесть один из них всем остальным? Если коротко, то это зависит от того, что вы делаете и как собираетесь манипулировать данными. Например, матрица смежности великолепна и проста в использовании, но может занимать гораздо больше памяти, чем, скажем, список ребер. Обратите внимание и на то, что каждый метод годится для указания веса ребра в случае со взвешенным графом; эта информация была исключена из примеров для упрощения.
Заключение
Мир графов в компьютерных науках огромен. Возможно, для вас это было первое знакомство с ним. Надеемся, что теперь вы лучше сможете понять основы продвижения проектов.
Для дальнейшего погружения в тему рекомендуем изучить алгоритмы обхода, такие как DFS (поиск в глубину) и BFS (поиск в ширину).
Теория графов. Часть третья (Представление графа с помощью матриц смежности, инцидентности и списков смежности)
Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор
Список смежности (инцидентности)
Взвешенный граф (коротко)
Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.
Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).
Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).
Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.
Матрица смежности
Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.
Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.
Каждая ячейка матрицы равна либо 1, либо 0;
Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.
Для практического примера возьмем самый обыкновенный неориентированный граф:
А теперь представим его в виде матрицы:
Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.
С одной стороны объем памяти будет:
Но используя вышеописанный подход получается:
Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.
Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.
Если мы используем ориентированный граф, то кое-что меняется.
Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.
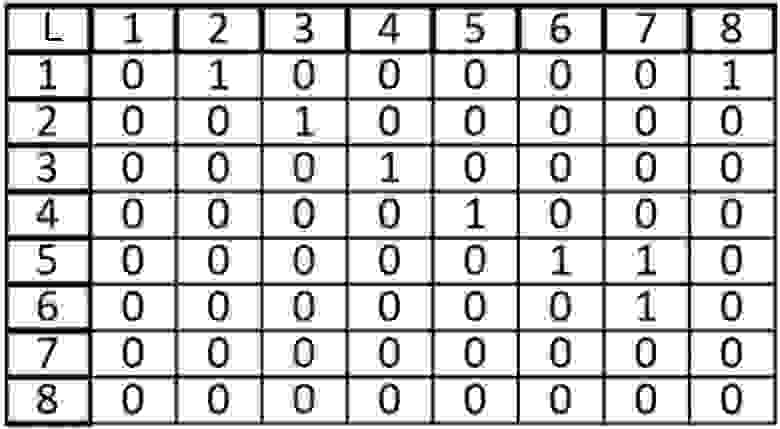
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:
Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.
Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.
Матрица инцидентности
Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.
Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.
Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.
Сразу же иллюстрируем данное правило:
Сумма элементов i-ой строки равна степени вершины.
Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.
Список смежности (инцидентности)
Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.
В виде списка это будет выглядеть так:
Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.
Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:
Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).
Сумма длин всех списков:
Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.
К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.
Взвешенность графа
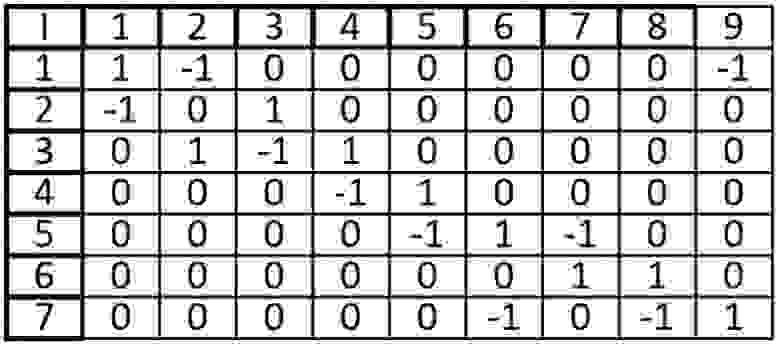
К примеру, возьмем граф с весами на ребрах:
И сделаем матрицу смежности:
В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.
Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.
Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.
Если заметили ошибку или есть предложения пишите в комментарии.
Что такое взвешенные графы
Теория графов представляет собой раздел математики, имеющий широкое практическое применение во многих областях человеческой деятельности. Математика, физика, химия, теория связи, электротехника, архитектура, исследование операций, генетика, психология – вот далеко не полный список областей ее применени я
Теория графов становится одной из существенных частей математического аппарата кибернетики, языком дискретной математики.
Граф G задается с помощью пары множеств G = (V, R ), где V есть множество вершин, а R – множество линий, соединяющих пары вершин. Линии со стрелками называются дугами, без стрелок – ребрами. Обычно граф представляют с помощью схемы, на которой некоторые вершины соединены ребрами (дугами).
Вершинами могут служить объекты любой природы: будь то населенные пункты, компьютерные сети, элементы блок- схем алгоритмов. Под ребром могут подразумеваться дороги между соседними городами, линии связи между компьютерами.
Ребро и любая из его двух вершин называются инцидентными. Под степенью вершин подразумевается количество инцидентных ей ребер. Так, степень вершин V1 равно 3, а степень вершин V 5 равна 4.
Последовательность чередующихся ребер и вершин графа называется маршрутом. В графах можно выделить различные маршруты. Маршрут называется замкнутым, если вершины начала и конца маршрута совпадают. Если ребра и вершины, образующие маршрут различны, то такой маршрут называется цепью. Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.
Длина маршрута равна количеству ребер, входящих в него.
Граф называется связным, если любые две его вершины можно соединить маршрутом (или путем).
Граф, в котором направление линий принципиально называется ориентированным (орграф). В орграфе каждое ребро имеет одно направление. Такие ребра называются дугами. Для орграфа вводятся такие понятия, как входящая и исходящая степени вершины. Это соответственно число входящих в вершину дуг и число исходящих из нее дуг.
Взвешенный граф – это граф, в котором с вершинами и линиями связана некоторая дополнительная информация. Эта информация называется весом вершины или линии. Вес позволяет отобразить на графе не только структуру системы, но и различные свойства компонент или связей, количественная характеристика. Вес сети равен сумме весов ее ребер.
Плоским графом называется граф, изображенный на плоскости так, что никакие два его ребра (или, вернее, представляющие их кривые) геометрически не пересекаются нигде, кроме инцидентной им обоим вершины. Граф, изоморфный плоскому графу, называется планарным. Планарный граф можно определить еще так: граф планарен, если его можно уложить на плоскости. Рисунок графа, в котором никакие два его ребра не пересекаются, если не считать точками пересечения общие вершины, называют плоским представлением графа. Ясно, что плоское представление имеет только плоский граф. Обратно, у всякого плоского графа непременно найдется плоское представление. Плоские графы — это простые циклы, деревья, лес, а также граф, содержащий цикл, из вершин которого «выходят» деревья.
Примером неплоского графа может служить полный граф с пятью вершинами. Любые попытки начертить его плоское представление обернутся неудачей.
В качестве характеристики плоского представления графа вводится понятие грани. Гранью в плоском представлении графа G называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.
В данном графе часть плоскости, ограниченная простым циклом (1,2,3,4,1), является гранью, так как ребро (4,5), расположенное внутри грани, не образует цикла.
Не является гранью заштрихованная часть плоскости в данном примере, так как она содержит цикл, да к тому же эта часть плоскости не ограничена циклом. Ребро (1,2) является мостом, соединяющим циклы. Такие мосты называются перегородками.
В качестве грани можно рассматривать и часть плоскости, расположенную «вне» плоского представления графа. Она ограничена «изнутри» простым циклом и не содержит других циклов. Эту часть плоскости называют бесконечной гранью.
На рисунке часть бесконечной грани заштрихована. Всякое плоское представление графа либо не имеет бесконечной грани, либо имеет в точности одну бесконечную грань. Как особый случай вводится бесконечная грань в плоском представлении дерева и леса. В плоском представлении дерева и леса за грань принимают всю плоскость рисунка.
Два графа гомеоморфны (или тождественны с точностью до вершин степени 2), если они оба могут быть получены из одного и того же графа «включением» в его ребра новых вершин степени 2.
Для всякого плоского представления связного плоского графа без перегородок число вершин ( V ), число ребер ( Е ) и число граней с учетом бесконечной ( R ) связаны соотношением V –Е + R = 2 .
Пусть граф G — связный, плоский граф без перегородок. Определим значение алгебраической суммы V –Е + R для его произвольного плоского представления.
Рассмотрим плоский граф G с пятью вершинами.
Если добавить к нему ребра (1, 3) и (1,5) и, то полученный новый граф G тоже будет плоским.
К этому графу не удается добавить ни одного ребра так, чтобы новый граф тоже был плоским.
Плоский граф называется максимально плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный граф был плоским. Изображенный граф является максимально плоским.
Каждая грань в плоском представлении максимально плоского графа имеет 3 вершины. Поэтому максимально плоский граф называют триангулированным. Операция добавления новых ребер, в результате которой в плоском представлении каждая грань имеет ровно 3 вершины, называется триангуляцией графа.
Преобразование графа в остовное связное дерево минимального веса.
Введем понятие цикломатического числа y, показывающего, сколько ребер графа нужно удалить, чтобы в нем не осталось ни одного цикла. Цикломатическое число y равно увеличенной на единицу разности между количеством ребер и количеством вершин графа:
Для каждого графа обычно существует несколько осотвных связных деревьев, которые обладают различными весами.
Для построения остовного связного дерева минимального веса используют алгоритм Крускала:
а) обе вершины включаемого графа принадлежат одноэлементным подмножествам, тогда они объединяются в новое, связное подмножество.
б) одна из вершин принадлежит связному подмножеству, а другая нет, тогда включаем вторую в подмножество, которому принадлежит первая.
в) обе вершины принадлежат разным связным подмножествам, тогда объединяем подмножества.
г) обе вершины принадлежат одному связному подмножеству, тогда исключаем данное ребро.
4. Алгоритм заканчивает работу, когда все вершины будут объединены ы одно множество, при этом оставшиеся ребра не включаются в оставное дерево.
Что такое взвешенный граф в информатике
Вы будете перенаправлены на Автор24
Взвешенный граф в информатике — это граф с вершинами или рёбрами, несущими добавочную информацию, другими словами вес.
Взвешенный граф
Под взвешенным графом понимается граф, у которого рёбрам соответствуют некоторые весовые параметры. То есть каждому ребру (дуге) поставлено в соответствие некое числовое значение, которое называется длина дуги (или вес, стоимость). Обычные графы (не взвешенные) тоже возможно представить в виде взвешенных, если считать, что все их рёбра обладают весом равным единице. Под длиной пути во взвешенном графе понимается суммарная длина (вес) рёбер, составляющих данный путь. Расстоянием между вершинами считается дистанция самого короткого по весу пути. На рисунке один приведён пример взвешенного графа и там можно видеть, что расстояние между вершинами a и d равняется шести. То есть это путь с наименьшим суммарным весом (от вершины a и далее b, c, d).
Рисунок 1. Образец взвешенного графа. Автор24 — интернет-биржа студенческих работ
Эйлеровы и гамильтоновы графы
Если в составе графа есть цикл (возможно и не простой), который содержит каждое ребро графа один раз, то этот цикл носит название эйлеровый цикл, и, соответственно, такой граф именуется эйлеровым.
Если в составе графа существует цепь, которая содержит каждую вершину один раз, то эта цепь считается эйлеровой цепью, а граф называется полуэйлеровым.
Эти формулировки появились в 1735-ом году в работе Эйлера, где он искал решение задачи о Кёнигсбергских мостах и там первым привёл термин граф. На рисунке два изображена схема, где представлены семь мостов в городе Кёнигсберг (сегодня это Калининград). По условиям задачи требуется пересечь каждый из мостов только один раз и выполнить возврат в начальную точку С. Так как обход мостов завешается в начальной точке маршрута и есть условие однократного пересечения каждого моста, то такой маршрут можно считать простым циклом, который содержит все рёбра графа. Позже подобные циклы получили название эйлеровых, а графы, в составе которых есть такие циклы, назвали эйлеровыми графами.
Готовые работы на аналогичную тему
Рисунок 2. Задача Эйлера о Кёнигсбергских мостах. Автор24 — интернет-биржа студенческих работ
На этом рисунке а — схема местоположения семи мостов в Кёнигсберге (сегодня Калининграде); б — граф, изображающий семь мостов в Кёнигсберге. Мосты представляют собой ребра графа, вершины отображают районы города, которые соединяют мосты.
Цикл Эйлера возможно представить как след от пера, которое рисует данный граф без отрыва пера от листа. То есть, иначе говоря, эйлеровы графы представляют собой графы, которые возможно нарисовать одним движением пера. При этом сам процесс рисования имеет начало и окончание в одной точке.
Выяснив, что в этом графе нет циклических обходов, которые проходят по каждому ребру один раз, Эйлер решил поставить задачу в более общей формулировке: какие должны выполняться условия, чтобы такой цикл в графе мог быть обнаружен? Ответ на поставленный вопрос Эйлер дал в своей теореме. Теорема Эйлера: для существования в связанном неориентированном графе G эйлерова цикла, необходимо и достаточно, чтобы количество вершин с нечётной степенью не превышало две.
Цепью Гамильтона в графе считается простая цепь, проходящая через каждую вершину графа строго по одному разу. Цикл графа, который проходит через все его вершины, считается гамильтоновым циклом. Гамильтоновым называют граф, у которого есть гамильтонов цикл. Гамильтоновы графы возможно использовать для построения моделей большого числа задач практики. К примеру, такие графы могут моделировать движение поездов, и это поможет составить оптимальное расписание их движения. Базой подобных задач является классическая проблема коммивояжера, которому необходимо выполнить вояж по городам и возвратиться в исходную точку, посетив каждый город только один раз. Затраты на поездку должны быть минимальными.