Что такое взвешенный граф информатика

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Графы

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)

§17. Графы.

Что такое граф?

Ключевые слова:

Давайте подумаем, как можно наглядно представить такую информацию:

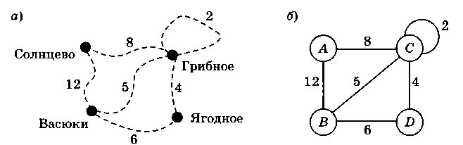
От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.

Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17

В информатике для исследования таких схем используют графы.

Граф — это набор вершин (узлов) и связей между ними — рёбер.

Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.

Матрица смежности графа

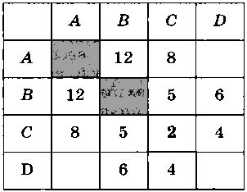
Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18

Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).

Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?

В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.

Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).

Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?

Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19

Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20

Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?

Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?

Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?

Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?

Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?

Связный граф

В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.

Связный граф — это граф, между любыми вершинами которого существует путь.

Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21

Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.

Постройте матрицу смежности графа, изображённого на рис. 3.21.

Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.

Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.

Найдите все циклы в графе на рис. 3.17.

Дерево — это связный граф, в котором нет циклов.

Взвешенный граф

Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

Рис. 3.23

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

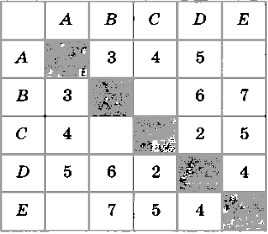
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24

Оптимальный путь в графе

Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.

Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?

Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25

Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.

Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26

Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27

Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?

Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.

Почему нельзя на этом остановиться, ведь путь из А в В найден?

Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28

Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.

Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29

Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.

Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?

Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.

Ориентированный граф

Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.

Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.

Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.

На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30

Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.

Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31

Количество путей

Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32

Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.

В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.

По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?

Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33

Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34

В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35

Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36

Выводы

• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.

Нарисуйте в тетради интеллект-карту этого параграфа.

Вопросы и задания

1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.

Подготовьте сообщение

а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»

Источник

Что такое взвешенный граф в информатике

Вы будете перенаправлены на Автор24

Взвешенный граф в информатике — это граф с вершинами или рёбрами, несущими добавочную информацию, другими словами вес.

Взвешенный граф

Под взвешенным графом понимается граф, у которого рёбрам соответствуют некоторые весовые параметры. То есть каждому ребру (дуге) поставлено в соответствие некое числовое значение, которое называется длина дуги (или вес, стоимость). Обычные графы (не взвешенные) тоже возможно представить в виде взвешенных, если считать, что все их рёбра обладают весом равным единице. Под длиной пути во взвешенном графе понимается суммарная длина (вес) рёбер, составляющих данный путь. Расстоянием между вершинами считается дистанция самого короткого по весу пути. На рисунке один приведён пример взвешенного графа и там можно видеть, что расстояние между вершинами a и d равняется шести. То есть это путь с наименьшим суммарным весом (от вершины a и далее b, c, d).

Рисунок 1. Образец взвешенного графа. Автор24 — интернет-биржа студенческих работ

Эйлеровы и гамильтоновы графы

Если в составе графа есть цикл (возможно и не простой), который содержит каждое ребро графа один раз, то этот цикл носит название эйлеровый цикл, и, соответственно, такой граф именуется эйлеровым.

Если в составе графа существует цепь, которая содержит каждую вершину один раз, то эта цепь считается эйлеровой цепью, а граф называется полуэйлеровым.

Эти формулировки появились в 1735-ом году в работе Эйлера, где он искал решение задачи о Кёнигсбергских мостах и там первым привёл термин граф. На рисунке два изображена схема, где представлены семь мостов в городе Кёнигсберг (сегодня это Калининград). По условиям задачи требуется пересечь каждый из мостов только один раз и выполнить возврат в начальную точку С. Так как обход мостов завешается в начальной точке маршрута и есть условие однократного пересечения каждого моста, то такой маршрут можно считать простым циклом, который содержит все рёбра графа. Позже подобные циклы получили название эйлеровых, а графы, в составе которых есть такие циклы, назвали эйлеровыми графами.

Готовые работы на аналогичную тему

Рисунок 2. Задача Эйлера о Кёнигсбергских мостах. Автор24 — интернет-биржа студенческих работ

На этом рисунке а — схема местоположения семи мостов в Кёнигсберге (сегодня Калининграде); б — граф, изображающий семь мостов в Кёнигсберге. Мосты представляют собой ребра графа, вершины отображают районы города, которые соединяют мосты.

Цикл Эйлера возможно представить как след от пера, которое рисует данный граф без отрыва пера от листа. То есть, иначе говоря, эйлеровы графы представляют собой графы, которые возможно нарисовать одним движением пера. При этом сам процесс рисования имеет начало и окончание в одной точке.

Выяснив, что в этом графе нет циклических обходов, которые проходят по каждому ребру один раз, Эйлер решил поставить задачу в более общей формулировке: какие должны выполняться условия, чтобы такой цикл в графе мог быть обнаружен? Ответ на поставленный вопрос Эйлер дал в своей теореме. Теорема Эйлера: для существования в связанном неориентированном графе G эйлерова цикла, необходимо и достаточно, чтобы количество вершин с нечётной степенью не превышало две.

Цепью Гамильтона в графе считается простая цепь, проходящая через каждую вершину графа строго по одному разу. Цикл графа, который проходит через все его вершины, считается гамильтоновым циклом. Гамильтоновым называют граф, у которого есть гамильтонов цикл. Гамильтоновы графы возможно использовать для построения моделей большого числа задач практики. К примеру, такие графы могут моделировать движение поездов, и это поможет составить оптимальное расписание их движения. Базой подобных задач является классическая проблема коммивояжера, которому необходимо выполнить вояж по городам и возвратиться в исходную точку, посетив каждый город только один раз. Затраты на поездку должны быть минимальными.

Источник

Содержание урока

Взвешенный граф

Взвешенный граф

Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Следующая страница Оптимальный путь в графе

Cкачать материалы урока

Источник

Что такое взвешенный граф информатика

Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.

Классификация графов

В связном графе между любой парой вершин существует как минимум один путь.

В несвязном графе существует хотя бы одна вершина, не связанная с другими.

Графы также подразделяются на

В ориентированном графе ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.

В неориентированном графе по каждому из ребер можно осуществлять переход в обоих направлениях.

Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер.

Способы представления графа

Граф может быть представлен (сохранен) несколькими способами:

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Размер массива зависит от количества вершин и/или ребер в конкретном графе.

Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.
Число строк матрицы смежности равно числу столбцов и соответствует количеству вершин графа.

Когда из одной вершины в другую проход свободен (имеется ребро), в ячейку заносится 1, иначе – 0. Все элементы на главной диагонали равны 0 если граф не имеет петель.

Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).

В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.

Матрица инцидентности для своего представления требует нумерации рёбер, что не всегда удобно.

Список смежности (инцидентности)
Если количество ребер графа по сравнению с количеством вершин невелико, то значения большинства элементов матрицы смежности будут равны 0. При этом использование данного метода нецелесообразно. Для подобных графов имеются более оптимальные способы их представления.

По отношению к памяти списки смежности менее требовательны, чем матрицы смежности. Такой список можно представить в виде таблицы, столбцов в которой – 2, а строк — не больше, чем вершин в графе.
В каждой строке в первом столбце указана вершина выхода, а во втором столбце – список вершин, в которые входят ребра из текущей вершины.

Преимущества списка смежности:

Недостатки списка смежности:

Алгоритмы обхода графов

Основными алгоритмами обхода графов являются

Поиск в ширину подразумевает поуровневое исследование графа:

Вершины просматриваются в порядке возрастания их расстояния от корня.
Алгоритм прекращает свою работу после обхода всех вершин графа, либо в случае выполнения требуемого условия (например, найти кратчайший путь из вершины 1 в вершину 6).
Каждая вершина может находиться в одном из 3 состояний:

Фиолетовый – рассматриваемая вершина.

Применения алгоритма поиска в ширину

Алгоритм поиска в ширину работает как на ориентированных, так и на неориентированных графах.
Для реализации алгоритма удобно использовать очередь.

Реализация на C++ (с использованием очереди STL)

Результат выполнения

Задача поиска кратчайшего пути
Реализация на С++

Поиск в глубину – это алгоритм обхода вершин графа.

Поиск в ширину производится симметрично (вершины графа просматривались по уровням). Поиск в глубину предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность продвижения означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина).

Отсутствие последнего свидетельствует об одной из двух возможных ситуаций:

Каждая вершина может находиться в одном из 3 состояний:

Фиолетовый – рассматриваемая вершина.

Применения алгоритма поиска в глубину

Алгоритм поиска в глубину работает как на ориентированных, так и на неориентированных графах. Применимость алгоритма зависит от конкретной задачи.
Для реализации алгоритма удобно использовать стек или рекурсию.

Реализация на C++ (с использованием стека STL)

Результат выполнения

Задача поиска лексикографически первого пути на графе.
Реализация на C++

Результат выполнения

Поиск в глубину также может быть реализован с использованием рекурсивного алгоритма.

Реализация обхода графа в глубину на C++ (с использованием рекурсии)

Источник