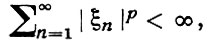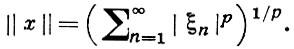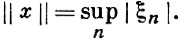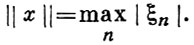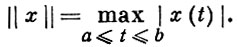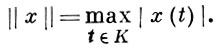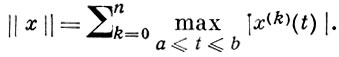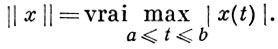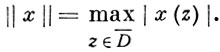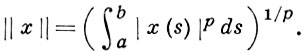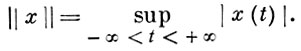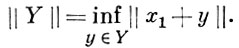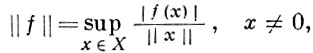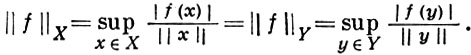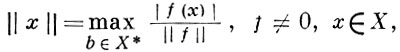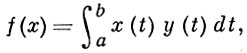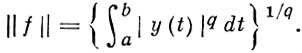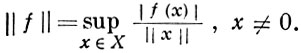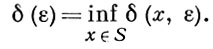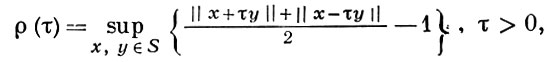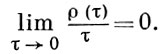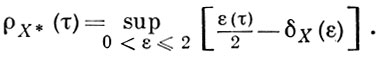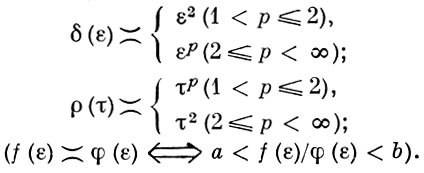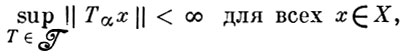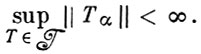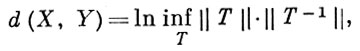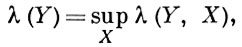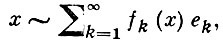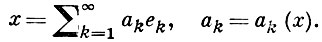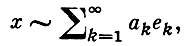Что такое банахово пространство

Банахово пространство

Ба́нахово пространство — нормированное векторное пространство, полное по метрике, порождённой нормой. Основной объект изучения функционального анализа. Названо по имени польского математика Стефана Банаха.

Примеры

Далее через обозначено одно из полей или .

Типы банаховых пространств

Полезное

Смотреть что такое «Банахово пространство» в других словарях:

БАНАХОВО ПРОСТРАНСТВО — В пространство, полное нормированное векторное пространство. Исходными для создания теории Б. п. послужили введенные (в 1904 18) Д. Гильбертом (D. Hilbert), М. Фреше (М. Frechet) и Ф. Рисом (F. Riesz) функциональные пространства. Именно в этих… … Математическая энциклопедия

Банахово пространство — (по имени С. Банаха полное нормированное Линейное пространство … Большая советская энциклопедия

БАНАХОВО АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО — бесконечномерное обобщение понятия аналитнч. пространства, возникшее в связи с изучением деформаций аналитических структур. Локальной моделью здесь служит банахово аналитическое множество, т. е. подмножество открытого множества Uв банаховом… … Математическая энциклопедия

Пространство Гильберта — Гильбертово пространство особый тип банаховых пространств, обобщение евклидова пространства на бесконечномерный случай. При этом гильбертово пространство не обязательно является бесконечномерным. Гильбертово пространство есть банахово… … Википедия

Пространство (физика) — Пространство понятие, используемое (непосредственно или в составе сложных терминов) в естественных языках, а также в таких разделах знания, как философия, математика, физика и т. п. На уровне повседневного восприятия пространство интуитивно… … Википедия

Пространство (значения) — Пространство понятие, используемое (непосредственно или в словосочетаниях) в обыденной речи, а также в различных разделах знаний. Пространство на уровне повседневного восприятия Математика Трёхмерное пространство Аффинное пространство Банахово… … Википедия

Пространство (математика) — У этого термина существуют и другие значения, см. Пространство. В математике слово «пространство» употребляется в большом наборе сложных терминов. Грубо говоря, пространство есть множество с некоторой дополнительной структурой. В зависимости от… … Википедия

Источник

БАНАХОВО ПРОСТРАНСТВО

Расстановка ударений: БАНА`ХОВО ПРОСТРА`НСТВО

Теория Б. п. развивалась параллельно с общей теорией линейных топологических пространств. Эти теории взаимно обогащались идеями и фактами. Так, идея полунормы, заимствованная из теории нормированных пространств, стала необходимым инструментом для построения теории локально выпуклых линейных топологич. пространств. Понятие слабой сходимости элементов и линейных функционалов в Б. п. обрело законченную форму в понятии слабой топологии. Теория Б. п. представляет собой хорошо разработанную область функционального анализа, имеющую (непосредственно или через теорию операторов) многочисленные применения в различных разделах математики.

Проблематика Б. п. складывается из нескольких направлений: геометрия единичной сферы, геометрия подпространств, линейно топологич. классификация, ряды и последовательности в Б. п., наилучшие приближения в Б. п., функции со значениями в Б. п. и др. Относительно теории операторов в Б. п. следует отметить, что многие ее предложения имеют непосредственное отношение к геометрии и топологии Б. п.

Пространства С [a, b], С n [а, b], L_p [a, b], с, l_p сепарабельны; пространства М [а, b], тm, АР несепарабельны; С [K] сепарабельно в том и только в том случае, если К-метрический компакт.

наз. пространством, сопряженным с X, и обозначается X*. Оно является Б. п.

Для Б. п. справедлива Хана-Банаха теорема о продолжении линейных функционалов: если линейный функционал определен на подпространстве Y нормированного пространства X, то его можно распространить с сохранением линейности и непрерывности на все пространство X. Более того, при этом можно обеспечить сохранение нормы расширенного функционала:

Справедливо и более общее утверждение: пусть действительная функция р(х), определенная в линейном пространстве, удовлетворяет условиям:

p(х + y) ≤ p(x) + p(y), р(λ х) = λ р(х), λ ≥ 0, х, у ∈ Х,

Тогда существует линейный функционал F(x), определенный на всем X и такой, что

F(x) = f(x) для х ∈ Y; F(x) ≤ р(х) для х ∈ Y.

Следствием теоремы Хана-Банаха является «обратная» формула, связывающая нормы X и X*:

Для многих конкретных Б. п. известен общий вид линейного функционала. Так, в L_p [a, b], (р > 1) каждый линейный функционал определяется по формуле:

где y ∈ L_q [a, b], 1/p + 1/q = 1, а каждая функция y(t) ∈ L_q определяет по этой формуле линейный функционал f, причем

Пространство X**, сопряженное с X*, наз. вторым сопряженным. Аналогично определяются третье, четвертое и т. д. сопряженные пространства. Каждый элемент из X может быть отождествлен с нек-рым линейным функционалом, определенным на X*:

F(f) = f(х), ∀ f ∈ X* (F ∈ X**, х ∈ Х).

Критерии рефлексивности Б. п. 1) X рефлексивно тогда и только тогда, когда для каждого f ∈ X* найдется х ∈ Х, на к-ром достигается sup в формуле

2) В рефлексивных Б. п., и только в них, каждое ограниченное множество компактно относительно слабой сходимости: любая его бесконечная часть содержит слабо сходящуюся подпоследовательность (теорема Эберлейна-Шмульяна). Пространства L_p и l_p, р > 1, рефлексивны. Пространства L₁, l₁, С, М, с, m, АР нерефлексивны.

Б. п. наз. строго нормированным, если его единичная сфера S не содержит отрезков. Для количественной оценки выпуклости единичного шара вводятся модули выпуклости: локальный модуль выпуклости и равномерный модуль выпуклости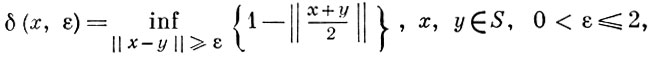

Если δ (х, ε) > 0 для всех х ∈ X и всех ε > 0, то Б. п. наз. локально равномерно выпуклым. Если δ (ε) > 0, то пространство наз. равномерно выпуклым. Каждое равномерно выпуклое Б. п. локально равномерно выпукло; каждое локально равномерно выпуклое Б. п. строго нормировано. В конечномерных Б. п. верны и обратные включения. Если Б. п. равномерно выпукло, то оно рефлексивно.

Б. п. наз. гладким, если для любых линейно независимых элементов х и у функция ψ (t) = ||x + ty|| дифференцируема при всех t. Б. п. наз. равномерно гладким, если для его модуля гладкости

В равномерно гладких Б. п., и только в них, норма равномерно дифференцируема по Фреше. Равномерно гладкое Б. п. гладко. Обратное верно, если Б. п. конечномерно, Б. п. X равномерно выпукло (равномерно гладко) в том и только в том случае, если X* равномерно гладко (равномерно выпукло). Между модулем выпуклости Б. п. А и модулем гладкости X* существует связь

Если Б. п. равномерно выпукло (равномерно гладко), то таковы любое его подпространство и факторпространство. Б. п. L_p и l_p (р > 1) равномерно выпуклы и равномерно гладки, причем

Б. п. М, С. A, L₁, АР, m, с, l₁ не являются строго нормированными и не являются гладкими.

В Б. п. справедливы следующие важные теоремы для линейных операторов:

Теорема Банаха-Штейнхауз а. Если семейство линейных операторов 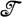= <Т_α> ограничено в каждой точке:

то оно ограничено по норме:

Теорема о замкнутом графике. Если замкнутый линейный оператор отображает Б. п. X в Б. п. Y, то он непрерывен.

где Т пробегает всевозможные операторы, осуществляющие изоморфизм между X и Y. Если X изометрично Y, то d(X, Y) = 0. Однако существуют и не изометричные пространства, для к-рых d(X, Y) = 0; их наз. почти изометричными. Свойства Б. п., сохраняющиеся при изоморфизме, наз. линейно топологическими. К ним относятся сепарабельность, рефлексивность, слабая полнота. Изоморфная классификация Б. п. содержит, в частности, следующие утверждения:

С [K] = С [0, 1], если К-метрич. компакт мощности континуума;

Каждое сепарабельное Б. п. изоморфно локально равномерно выпуклому. Неизвестно (1977), каждое ли Б. п. изоморфно своей гиперплоскости. Существует Б. п., не изоморфное строго нормированному.

Отвлекаясь от линейной природы нормированных пространств, можно рассматривать их топология, классификацию. Два пространства гомеоморфны, если между их элементами может быть установлено взаимно однозначное и взаимно непрерывное (не обязательно линейное) соответствие. Неполное нормированное пространство не гомеоморфно никакому Б. п. Все бесконечномерные сепарабельные Б. п. гомеоморфны.

Универсальными (см. Универсальное пространство) в классе сепарабельных Б. п. являются С [0, 1] и A (D). В классе рефлексивных сепарабельных Б. п. нет даже изоморфно универсального. Б. п. l 1 универсально в несколько ином смысле: каждое сепарабельное Б. п. изометрично нек-рому его факторпространству.

В каждом из перечисленных выше Б. п., кроме L₂ и l₂, существуют подпространства без дополнения. В частности, в m и М не дополняемо каждое бесконечномерное сепарабельное подпространство, в С [0, 1] не дополняемо каждое бесконечномерное рефлексивное подпространство. Если в Б. п. все подпространства дополняемы, то оно изоморфно гильбертову пространству. Неизвестно (1977), каждое ли Б. п. есть прямая сумма каких-то двух бесконечномерных подпространств. Подпространство Y дополняемо в том и только в том случае, если существует проектор, отображающий X на Y. Относительной проекционной константой λ (Y, X) подпространства Y в X наз. нижняя грань норм проекторов на Y. Каждое n-мерное подпространство Б. п. дополняемо и λ (Y_n, X) ≤ √n Абсолютной проекционной константой λ (Y) Б. п. Y наз.

где X пробегает все Б. п., содержащие Y в качестве подпространства. Для любого бесконечномерного сепарабельного Б. п. Y имеем λ (Y) = ∞. Б. п., для к-рых λ (Y) ≤ λ 2 _k ∞ Б. п. наз. минимальной, если любой ее член лежит вне замыкания X (n) = [e_k ]_{k ≠ n} линейной оболочки остальных членов. Последовательность наз. равномерно минимальной, если

однако в общем случае этот ряд расходится.

Система элементов k> ∞ ₁ наз. базисом в X, если каждый элемент х ∈ Х может быть единственным обра зом представлен в виде сходящегося ряда

Лит. : [1] Ваnасh S., «Fund. math. », 1922, t. 3, p. 133-81; [2] Банах С. С., Курс функцiонального аналiзу, Киiв, 1948; [3] Данфорд Н., Шварц Дж. Т., Линейные операторы. Общая теория, пер. с англ., М., 1962; [4] Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961; [5] Бурбаки Н., Топологические векторные пространства, пер. с франц., М., 1959.

М. И. Кадец, Б. М. Левитан.

Источник

Банахово пространство

СОДЕРЖАНИЕ

Определение [ править ]

Полнота [ править ]

Полные нормы vs полные метрики

Полные нормы против полных топологических векторных пространств

Характеристика по сериям

Завершенные [ править ]

Каждое нормированное пространство может быть изометрически вложено в плотное векторное подпространство некоторого банахова пространства, где это банахово пространство называется пополнением нормированного пространства. Это хаусдорфово пополнение единственно с точностью до изометрического изоморфизма.

Общая теория [ править ]

Линейные операторы, изоморфизмы [ править ]

Основные понятия [ править ]

Декартово произведение X × Y двух нормированных пространств канонически не снабжено нормой. Однако обычно используются несколько эквивалентных норм [11], таких как

и порождают изоморфные нормированные пространства. В этом смысле произведение X × Y (или прямая сумма X ⊕ Y ) является полным тогда и только тогда, когда два множителя полны.

Классические пространства [ править ]

Банаховы алгебры [ править ]

Примеры [ править ]

Двойной пробел [ править ]

В частности, любой непрерывный линейный функционал на подпространстве нормированного пространства можно непрерывно продолжить на все пространство без увеличения нормы функционала. [17] Важным частным случаем является следующий: для каждого вектора x в нормированном пространстве X существует непрерывный линейный функционал f на X такой, что

Двойственное к сепарабельному банахову пространству не обязательно должно быть сепарабельным, но:

Слабые топологии [ править ]

Теорема Банаха – Алаоглу зависит от теоремы Тихонова о бесконечных произведениях компактных пространств. Когда X отделимо, единичный шар B ′ дуального является метризуемым компактом в слабой * топологии. [24]

Примеры двойных пробелов [ править ]

Двойственный элемент c ₀ изометрически изоморфен ℓ 1 : для любого ограниченного линейного функционала f на c ₀ существует единственный элемент y = < y _n > ∈ ℓ 1 такой, что

Для любого вектора y в гильбертовом пространстве H отображение

Двусторонний [ править ]

Теоремы Банаха [ править ]

Этот результат является прямым следствием предыдущей теоремы об изоморфизме Банаха и канонической факторизации ограниченных линейных отображений.

Рефлексивность [ править ]

Нормированное пространство X называется рефлексивным, если естественное отображение

В самом деле, если двойственное Y ′ банахова пространства Y сепарабельно, то Y сепарабельно. Если X рефлексивно и отделимо, то двойственное к X ′ сепарабельно, поэтому X ′ сепарабельно.

Теорема может быть расширена, чтобы дать характеристику слабо компактных выпуклых множеств.

Слабые сходимости последовательностей [ править ]

Теорема. [35] Для любой меры µ пространство L 1 ( µ ) слабо секвенциально полно.

Результаты на основе ℓ 1 [ править ]

Дополнение к этому результату принадлежит Odell and Rosenthal (1975).

Последовательности, слабая и слабая * компактность [ править ]

Слабая топология банахова пространства X метризуема тогда и только тогда, когда X конечномерно. [43] Если двойственное X ′ сепарабельно, слабая топология единичного шара X метризуема. В частности, это относится к сепарабельным рефлексивным банаховым пространствам. Хотя слабая топология единичного шара, вообще говоря, не метризуема, слабую компактность можно охарактеризовать с помощью последовательностей.

Банахово пространство X рефлексивно тогда и только тогда, когда каждая ограниченная последовательность в X имеет слабо сходящуюся подпоследовательность. [45]

Базы Шаудера [ править ]

Тензорный продукт [ править ]

Существуют различные нормы, которые могут быть помещены в тензорное произведение лежащих в основе векторных пространств, в том числе проективная кросс-норма и инъективная кросс-норма, введенные А. Гротендиком в 1955 году [51].

Тензорные произведения и свойство аппроксимации [ править ]

Для любого банахова пространства Y существует линейное отображение с естественной нормой 1

X ′ ⊗ ^ π X ⟶ X ′ ⊗ ^ ε X <\displaystyle X'<\widehat <\otimes >>_<\pi >X\ \longrightarrow X’<\widehat <\otimes >>_<\varepsilon >X>

взаимно однозначно тогда и только тогда, когда X обладает свойством аппроксимации. [55]

Некоторые результаты классификации [ править ]

Характеризации гильбертова пространства среди банаховых пространств [ править ]

Необходимым и достаточным условием для того, чтобы норма банахова пространства X была ассоциирована со скалярным произведением, является тождество параллелограмма :

Доступны несколько характеристик пространств, изоморфных (а не изометричных) гильбертовым пространствам. Закон параллелограмма может быть расширен более чем на два вектора и ослаблен введением двустороннего неравенства с константой c ≥ 1 : Квапень доказал, что если

c − 2 ∑ k = 1 n ‖ x k ‖ 2 ≤ Ave ± ⁡ ‖ ∑ k = 1 n ± x k ‖ 2 ≤ c 2 ∑ k = 1 n ‖ x k ‖ 2 <\displaystyle c^<-2>\sum _^\left\|x_\right\|^<2>\leq \operatorname _<\pm >\left\|\sum _^\pm x_\right\|^<2>\leq c^<2>\sum _^\left\|x_\right\|^<2>>

Теорема. [61] Банахово пространство, изоморфное всем своим бесконечномерным замкнутым подпространствам, изоморфно сепарабельному гильбертову пространству.

Метрическая классификация [ править ]

Топологическая классификация [ править ]

Конечномерные банаховы пространства гомеоморфны как топологические пространства тогда и только тогда, когда они имеют ту же размерность, что и вещественные векторные пространства.

Пространства непрерывных функций [ править ]

Иная ситуация для счетно бесконечных компактных хаусдорфовых пространств. Каждый счетно бесконечный компакт K гомеоморфен некоторому отрезку порядковых чисел

Примеры [ править ]

Производные [ править ]

Обобщения [ править ]

Источник

Банахово пространство

СОДЕРЖАНИЕ

Определение [ править ]

Полнота [ править ]

Полные нормы vs полные метрики

Полные нормы против полных топологических векторных пространств

Характеристика по сериям

Завершенные [ править ]

Каждое нормированное пространство может быть изометрически вложено в плотное векторное подпространство некоторого банахова пространства, где это банахово пространство называется пополнением нормированного пространства. Это хаусдорфово пополнение единственно с точностью до изометрического изоморфизма.

Общая теория [ править ]

Линейные операторы, изоморфизмы [ править ]

Основные понятия [ править ]

Декартово произведение X × Y двух нормированных пространств канонически не снабжено нормой. Однако обычно используются несколько эквивалентных норм [11], таких как

и порождают изоморфные нормированные пространства. В этом смысле произведение X × Y (или прямая сумма X ⊕ Y ) является полным тогда и только тогда, когда два множителя полны.

Классические пространства [ править ]

Банаховы алгебры [ править ]

Примеры [ править ]

Двойной пробел [ править ]

В частности, любой непрерывный линейный функционал на подпространстве нормированного пространства можно непрерывно продолжить на все пространство без увеличения нормы функционала. [17] Важным частным случаем является следующий: для каждого вектора x в нормированном пространстве X существует непрерывный линейный функционал f на X такой, что

Двойственное к сепарабельному банахову пространству не обязательно должно быть сепарабельным, но:

Слабые топологии [ править ]

Теорема Банаха – Алаоглу зависит от теоремы Тихонова о бесконечных произведениях компактных пространств. Когда X отделимо, единичный шар B ′ дуального является метризуемым компактом в слабой * топологии. [24]

Примеры двойных пробелов [ править ]

Двойственный элемент c ₀ изометрически изоморфен ℓ 1 : для любого ограниченного линейного функционала f на c ₀ существует единственный элемент y = < y _n > ∈ ℓ 1 такой, что

Для любого вектора y в гильбертовом пространстве H отображение

Двусторонний [ править ]

Теоремы Банаха [ править ]

Этот результат является прямым следствием предыдущей теоремы об изоморфизме Банаха и канонической факторизации ограниченных линейных отображений.

Рефлексивность [ править ]

Нормированное пространство X называется рефлексивным, если естественное отображение

В самом деле, если двойственное Y ′ банахова пространства Y сепарабельно, то Y сепарабельно. Если X рефлексивно и отделимо, то двойственное к X ′ сепарабельно, поэтому X ′ сепарабельно.

Теорема может быть расширена, чтобы дать характеристику слабо компактных выпуклых множеств.

Слабые сходимости последовательностей [ править ]

Теорема. [35] Для любой меры µ пространство L 1 ( µ ) слабо секвенциально полно.

Результаты на основе ℓ 1 [ править ]

Дополнение к этому результату принадлежит Odell and Rosenthal (1975).

Последовательности, слабая и слабая * компактность [ править ]

Слабая топология банахова пространства X метризуема тогда и только тогда, когда X конечномерно. [43] Если двойственное X ′ сепарабельно, слабая топология единичного шара X метризуема. В частности, это относится к сепарабельным рефлексивным банаховым пространствам. Хотя слабая топология единичного шара в общем случае не метризуема, слабую компактность можно охарактеризовать с помощью последовательностей.

Банахово пространство X рефлексивно тогда и только тогда, когда каждая ограниченная последовательность в X имеет слабо сходящуюся подпоследовательность. [45]

Базы Шаудера [ править ]

Тензорный продукт [ править ]

Существуют различные нормы, которые могут быть помещены в тензорное произведение лежащих в основе векторных пространств, в том числе проективная кросс-норма и инъективная кросс-норма, введенные А. Гротендиком в 1955 году [51].

Тензорные произведения и свойство аппроксимации [ править ]

Для любого банахова пространства Y существует линейное отображение с естественной нормой 1

X ′ ⊗ ^ π X ⟶ X ′ ⊗ ^ ε X <\displaystyle X'<\widehat <\otimes >>_<\pi >X\ \longrightarrow X’<\widehat <\otimes >>_<\varepsilon >X>

взаимно однозначно тогда и только тогда, когда X обладает свойством аппроксимации. [55]

Некоторые результаты классификации [ править ]

Характеризации гильбертова пространства среди банаховых пространств [ править ]

Необходимым и достаточным условием для того, чтобы норма банахова пространства X была ассоциирована со скалярным произведением, является тождество параллелограмма :

Доступны несколько характеристик пространств, изоморфных (а не изометричных) гильбертовым пространствам. Закон параллелограмма может быть расширен более чем на два вектора и ослаблен введением двустороннего неравенства с константой c ≥ 1 : Квапень доказал, что если

c − 2 ∑ k = 1 n ‖ x k ‖ 2 ≤ Ave ± ⁡ ‖ ∑ k = 1 n ± x k ‖ 2 ≤ c 2 ∑ k = 1 n ‖ x k ‖ 2 <\displaystyle c^<-2>\sum _^\left\|x_\right\|^<2>\leq \operatorname _<\pm >\left\|\sum _^\pm x_\right\|^<2>\leq c^<2>\sum _^\left\|x_\right\|^<2>>

Теорема. [61] Банахово пространство, изоморфное всем своим бесконечномерным замкнутым подпространствам, изоморфно сепарабельному гильбертову пространству.

Метрическая классификация [ править ]

Топологическая классификация [ править ]

Конечномерные банаховы пространства гомеоморфны как топологические пространства тогда и только тогда, когда они имеют ту же размерность, что и вещественные векторные пространства.

Пространства непрерывных функций [ править ]

Иная ситуация для счетно бесконечных компактных хаусдорфовых пространств. Каждый счетно бесконечный компакт K гомеоморфен некоторому отрезку порядковых чисел

Примеры [ править ]

Производные [ править ]

Обобщения [ править ]

Источник