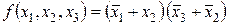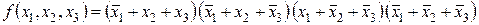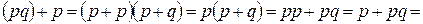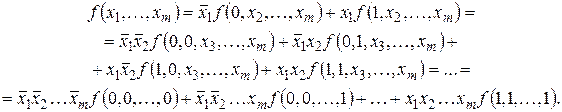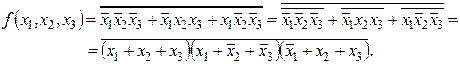Что такое базис логических элементов
Базис логических элементов
Правила алгебры логики позволяют преобразовать логическую функцию к виду, удобному для реализации в виде логического устройства.
Например, задана функция

Для реализации функции в данном виде требуется два инвертора НЕ, три трехвходовых элемента 3И, один трехвходовый элемент 3ИЛИ:
Проведем эквивалентные преобразования на основании правил (6), (13), (19)
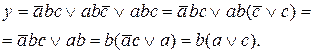
Очевидно, что после преобразования функция (22) значительно упростилась (23). Для ее реализации достаточно иметь один двухвходовый элемент 2И, один двухвходовый элемент 2ИЛИ (рис. б). Обе схемы (рис. а, б) позволяют реализовать одну и ту же функцию у.
При рассмотрении законов булевой алгебры использовались только три элементарные функции (НЕ, И, ИЛИ). Всего же существует 4 функции одной переменной и 16 функций двух переменных. Ранее отмечалось, что с помощью элементарных функций можно построить любую сложную логическую функцию.
Определение. Функционально полная система (базис) — совокупность логических элементов, которая позволяет реализовать любую логическую схему произвольной сложности.
Для построения сложной логической функции нет необходимости использовать все элементарные функции. Допустимо ограничить набор элементарных функций, исключая из него те элементы, которые можно выразить через другие. Последовательно исключая из базиса функции, получают минимальный базис.
Определение. Под минимальным базисом понимают такой набор функций, исключение из которого любой функции превращает полную систему в неполную.
Возможны различные базисы, отличающиеся друг от друга числом входящих в них функций и видом этих функций. Выбор того или иного базиса для построения логических устройств обусловлен тем, насколько экономически удобно и просто выполнить элементы, технически реализующие входящие в базис функции, и все логическое устройство в целом.
Через три логические функции инверсии (НЕ), конъюнкции (И), дизъюнкции (ИЛИ) можно выразить любую элементарную функцию и построить любое сложное логическое устройство. Набор из трех функций (НЕ, И, ИЛИ) является базисом. Однако, базис (НЕ, И, ИЛИ) не является минимальным. Из него можно исключить одну из функций И либо ИЛИ. Наборы (НЕ, И), а также (НЕ, ИЛИ) из двух функций служат базисами. Действительно функцию И можно реализовать через функции (НЕ, ИЛИ):

Функцию ИЛИ можно реализовать через функции (НЕ, И):

Ограничиваясь базисами (НЕ, И); (НЕ, ИЛИ) для выполнения исключенной одной операции требуется проводить дополнительно три операции НЕ, что экономически нецелесообразно. Поэтому на практике часто используют неминимальный базис трех функций (НЕ, И, ИЛИ).
Довольно удобно технически реализуются на микросхемах логические элементы, совмещающие в себе указанные функции. Удобство объясняется тем, что транзистор инвертирует фазу входного сигнала, изменяет ее на 180°. Это элементы И-НЕ (штрих Шеффера) и ИЛИ-НЕ (стрелка Пирса).
Каждый из элементов (И-НЕ), (ИЛИ-НЕ) в отдельности является функционально полным базисом, позволяет синтезировать любое сколь угодно сложное устройство. Рассмотрим реализацию функций НЕ, И, ИЛИ в базисе (ИЛИ-НЕ):

Для инверсии необходимо подать входной сигнал на оба входа. Для конъюнкции — сначала инвертировать входные сигналы, а затем применить операцию ИЛИ-НЕ. Для дизъюнкции — провести операцию ИЛИ-НЕ, после чего инвертировать полученный результат:
В базисе (И-НЕ) функции НЕ, И, ИЛИ получают следующим образом:

Легко заметить, что формулы (24), (25) подобны. Их схемное решение показано на рис.
Привлекательность базисов из одной логической функции (И-НЕ) либо (ИЛИ-НЕ) заключается в том, что все логическое устройство построено только на однотипных логических элементах. Получаем логическую схему, которая обладает регулярной структурой. Необходимо только осуществить коммутацию одинаковых логических элементов. Базисы на логических элементах (И-НЕ), (ИЛИ-НЕ) широко используются при проектировании устройств, удобны для реализации в больших интегральных схемах. Уменьшение номенклатуры до одного типа, таким образом, облегчает проектирование устройств. Дополнительные инверторы на входах улучшают нагрузочную способность и служат для формирования сигналов лог. 1 и лог. 0 достаточного уровня.
Логические элементы и понятие базиса
Логические элементы – устройства, с помощью которых реализуются логические функции. Логические элементы могут быть электрическими, пневматическими, световыми и струйными. Их используют для построения сложных преобразователей цифровых сигналов.
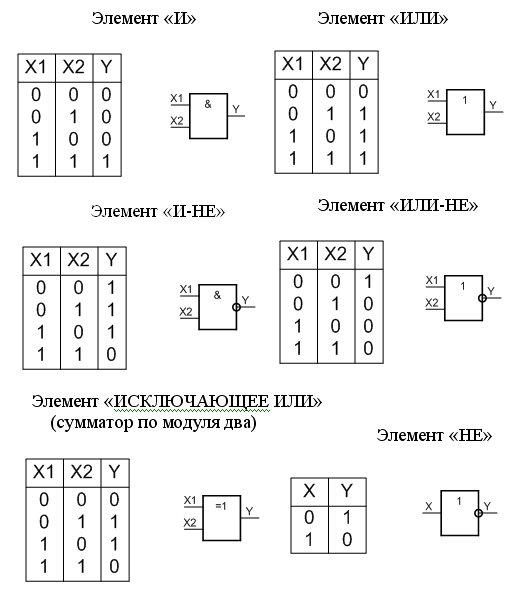
Изготовляются и используются в основном 6 типов логических элементов (остальные функции могут быть получены из этого набора). Таблицы истинности и их условное графическое обозначение элементов представлены на рисунке 1.1.
Рисунок 1.1 Таблицы истинности и условное графическое обозначение элементов
Набор логических элементов, с помощью которых можно реализовать любую функцию называется базисом.
Набор элементов И, ИЛИ, HЕ называют основным базисом.
Базисами являются также наборы элементов:
ИЛИ, НЕ; И, НЕ; И-НЕ; ИЛИ-НЕ;
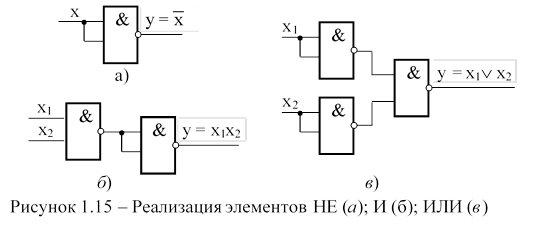
На рисунке 1.15 показан пример реализации логических элементов НЕ, И, ИЛИ в базисе И-НЕ.
Элемент НЕ реализован при использовании следующего соотношения:
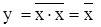
Элемент И реализован при использовании следующего соотношения:
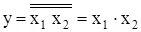
Элемент И реализован при использовании следующего соотношения:
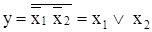
Базисы и формы представления логических функций



Базис (функционально полный набор) – это множество логических функций, суперпозицией которых можно представить любую логическую формулу, т. е. полная система логических функций.
Базисы могут быть избыточными и минимальными. Например, система функций И, Или, НЕ (булев базис, базис Буля) – избыточный базис, так как при удалении из него некоторых функций (функции ИЛИ или функции И) система остаётся полной.
Минимальными базисами являются системы: 1) И, НЕ; 2) ИЛИ, НЕ; 3) И-НЕ (базис Шеффера); 4) ИЛИ-НЕ (базис Пирса). При удалении из таких базисов любой операции они перестают быть полными системами функций.
В табл. 2.9 приведено несколько полезных свойств булевых функций НЕ, И, ИЛИ, формулы перехода между базисами И-НЕ и ИЛИ-НЕ (законы де Моргана), а также формулы перехода от операций импликация, тождественность и сумма по модулю 2 в базис Буля. Все приведённые соотношения можно легко проверить с помощью их таблиц истинности.
Таблица 2.9
| № | Формулы булевой алгебры | Формулы в упрощённой записи | Название свойства |
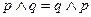 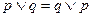 | 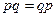 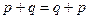 | Коммутативность (перемена мест операндов) | |
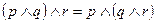  | 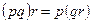 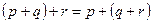 | Ассоциативность (последовательность выполнения операций) | |
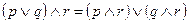 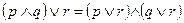 | 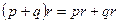 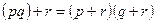 | Дистрибутивность (раскрытие скобок) | |
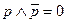 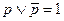 | 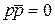 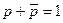 | Законы исключённого третьего | |
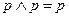 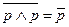 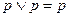 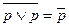 | 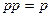 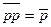 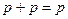 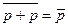 | Законы тождественных операндов | |
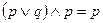 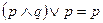 | 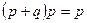 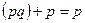 | Законы поглощения | |
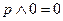 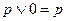 | 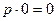 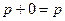 | Свойства нуля | |
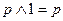 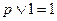 | 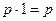 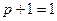 | Свойства единицы | |
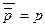 | Свойство двойного отрицания | ||
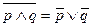 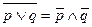 | 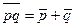 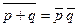 | Законы (формулы) де Моргана | |
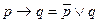 | 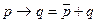 | Свойство импликации | |
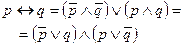 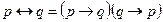 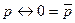 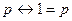 | 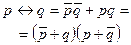 | Свойства эквивалентности | |
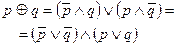 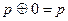 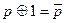 | 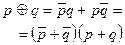 | Свойства сложения по модулю два |
Далее по возможности будем пользоваться упрощёнными обозначениями логических операций.
Докажем некоторые из приведённых свойств:
7. 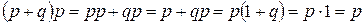
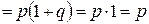
12. 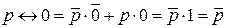
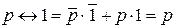
13. 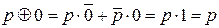
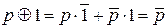
Введём понятие терма.
Терм – это дизъюнкция или конъюнкция любого числа переменных, взятых с отрицанием или без него. В терм в общем случае не обязательно должны входить все переменные, он даже может состоять только из одной переменной.
Термы, состоящие только из одной переменной, взятой с отрицанием или без него, называются первичными термами.
Ранг терма определяется количеством переменных, входящих в данный терм.
Терм в виде конъюнкции переменных, взятых с отрицанием или без него, называется конъюнктивным термом, конституентой единицы (любой такой терм, принимающий значение 1, автоматически приводит к единичному значению функции) или минтермом (для принятия функцией значения 1 требуется минимальное количество единичных термов, а точнее только один). Под минтермом обычно понимается конъюнктивный терм, содержащий все переменные логической функции.
Терм, являющийся дизъюнкцией логических переменных в прямом или инверсном виде, называется дизъюнктивным термом, конституентой нуля (любой такой терм, принимающий значение 0, автоматически приводит к нулевому значению функции) или макстермом (для принятия функцией значения 1 требуется максимальное количество единичных термов, а точнее всех термов). Под макстермом обычно понимается дизъюнктивный терм, содержащий все переменные логической функции.
Теорема 2.1. Любая логическая функция может быть представлена как суперпозиция только трёх функций: И, ИЛИ и НЕ.
Доказательство данной теоремы основано на лемме о дизъюнктивном разложении.
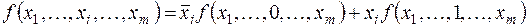
Действительно, при xi = 0 правая часть этой формулы принимает значение
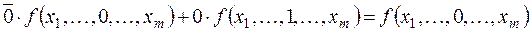
аналогично при xi = 1 правая часть
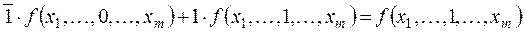
Итак, правая часть формулы (2.4) при всех наборах аргументов совпадает с левой, что доказывает справедливость формулы (2.4).
Таким образом, любую булеву функцию можно представить как дизъюнкцию термов, каждый из которых представляет собой конъюнкцию всех переменных (с отрицаниями или без них) и значения этой функции на соответствующем конкретном наборе значений переменных.
Примем для σ 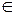
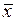
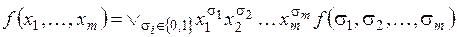
Поскольку значения функции на каждом конкретном наборе равны либо 0, либо 1, то в формуле (2.5) останутся только такие термы, которые соответствуют наборам переменных, на которых функция равна единице:
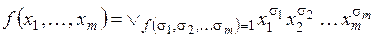
Представление булевой функции в форме дизъюнкции конъюнктивных термов (конституент единицы) Ki
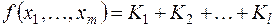
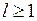
называется дизъюнктивной нормальной формой (ДНФ) этой функции.
Если все конъюнктивные термы в ДНФ являются минтермами, т. е. содержат в точности по одной все логические переменные, взятые с отрицаниями или без них, то такая форма представления функции называется совершенной дизъюнктивной нормальной формой (СДНФ) этой функции. СДНФ называется совершенной, потому что каждый терм в дизъюнкции включает все переменные; дизъюнктивной, потому что главная операция в формуле – дизъюнкция. Понятие “нормальной формы” означает однозначный способ записи формулы, реализующей заданную функцию.
С учётом сказанного выше из теоремы 2.1 вытекает следующая теорема.
Теорема 2.2. Любая булева функция ( не равная тождественно 0 ) может быть представлена в СДНФ, причём такое представление единственно.
Таблица 2.10
На основании формулы (2.6) получаем:
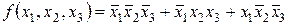
Как видно, при составлении СДНФ функции нужно составить дизъюнкцию всех минтермов, при которых функция принимает значение 1.
Представление булевой функции в форме конъюнкции дизъюнктивных термов (конституент нуля) Di
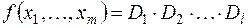
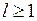
называется конъюнктивной нормальной формой (КНФ) этой функции.
Если все дизъюнктивные термы КНФ являются макстермами, т. е. содержат в точности по одной все логические переменные функции, взятые с отрицаниями или без них, то такая КНФ называется совершенной конъюнктивной нормальной формой (СКНФ) этой функции.
Теорема 2.3. Любая булева функция ( не равная тождественно 1 ) может быть представлена в СКНФ, причём такое представление единственно.
Доказательство теоремы может быть проведено аналогично доказательству теоремы 2.1 на основании следующей леммы Шеннона о конъюнктивном разложении.
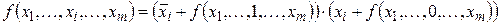
Нужно отметить, что обе формы представления логической функции (ДНФ и КНФ) теоретически являются равными по своим возможностям: любую логическую формулу можно представить как в ДНФ (кроме тождественного нуля), так и в КНФ (кроме тождественной единицы). В зависимости от ситуации представление функции в той или иной форме может быть короче.
В отличие от СДНФ, при составлении СКНФ в таблице истинности логической функции нужно смотреть комбинации переменных, при которых функция принимает значение 0, и составить конъюнкцию соответствующих макстермов, но переменные нужно брать с обратной инверсией:
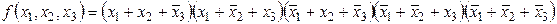
Нужно отметить, что непосредственно перейти от СДНФ функции к её СКНФ или наоборот невозможно. При попытке таких преобразований получаются функции, обратные по отношению к желаемым. Выражения для СДНФ и СКНФ функции непосредственно можно получить только из её таблицы истинности.
Используя результат примера 2.3 получим:
Как видно, под общей инверсией получилась СКНФ логической функции, которая является обратной по отношению к функции, полученной в примере 2.4:
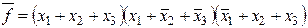
т. к. содержит все макстермы, которых нет в выражении для СКНФ рассматриваемой функции.
Далее приведём систематическую процедуру (алгоритм) преобразования аналитической записи функции в нормальную форму с использованием свойств булевых функций.
1. Используя свойства операций (см. табл. 2.9) тождественность ( 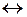
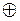
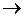
2. Используя свойства отрицания и законы де Моргана (см. табл. 2.9) добиваемся, чтобы операции отрицания относились только к отдельным переменным, а не к целым выражениям.
3. Используя свойства логических операций И и ИЛИ (см. табл. 2.9), получаем нормальную форму (ДНФ или КНФ).
4. При необходимости переходим к совершенным формам (СДНФ или СКНФ). Например, для получения СКНФ часто нужно использовать свойство: 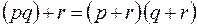
Пример 2.6. Преобразовать в СКНФ логическую функцию
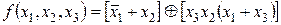
Выполняя по порядку шаги приведённого выше алгоритма, получим:
Используя свойство поглощения, получим: