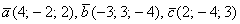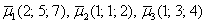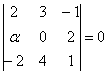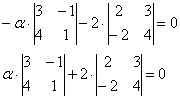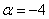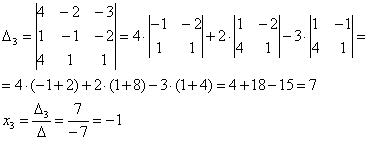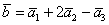Что такое базис пространства

29.10.202312.04.2022 admin 0 Comments

Размерность и базис линейного пространства

Определения размерности и базиса

Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов ( базисных векторов ).

и притом единственным образом, т.е. коэффициенты определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.

Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему векторов n-мерного линейного пространства можно дополнить до базиса пространства.

2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.

3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.

5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.

Примеры базисов линейных пространств

Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.

5. В пространстве матриц размеров можно выбрать 6 матриц:

которые линейно независимы. Действительно, их линейная комбинация

6. Для любого натурального в пространстве многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены линейно независимы, так как их линейная комбинация

Во-первых, покажем, что система линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов и приравняем ее нулевой функции

т.е. функция представлена в виде линейной комбинации функций (числа — коэффициенты линейной комбинации). Следовательно, система ковекторов является базисом сопряженного пространства и (для конечномерного пространства ).

Источник

Базис векторного пространства

Базис векторного пространства [basis of vector space] – набор из максимального (для данного пространства) числа линейно-независимых векторов. (см. Линейная зависимость векторов) Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы взаимно ортогональны, а длина каждого из них равна единице, то базис называется ортонормированным. Единичный базисный вектор называют ортом (обозначается e _i , где i – номер координаты).

Каждый вектор пространства может быть представлен в виде линейной комбинации базисных векторов: a = Σa _i e _i . Коэффициенты разложения a _i однозначно определяют вектор a. Поэтому часто говорят, что n-мерный вектор – это упорядоченная совокупность n чисел <a _i >. (См. Вектор). Размерность пространства равна количеству его базисных векторов.

Полезное

Смотреть что такое «Базис векторного пространства» в других словарях:

базис векторного пространства — Набор из максимального (для данного пространства) числа линейно независимых векторов (см. Линейная зависимость векторов). Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы… … Справочник технического переводчика

базис (векторного пространства) — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN basis … Справочник технического переводчика

Базис (векторного пространства) — такая линейно независимая система базисных векторов, что любой вектор, принадлежащий этому пространству, оказывается линейной комбинацией векторов этой системы … Начала современного естествознания

КОМПЛЕКСИФИКАЦИЯ ВЕКТОРНОГО ПРОСТРАНСТВА — комплексное векторное пространство VC, полученное из вещественного векторного пространства Vпутем расширения поля скаляров. Пространство VC определяется как тензорное произведение Его можно определить также как множество формальных выражений x+iy … Математическая энциклопедия

Размерность векторного пространства — Линейное пространство, или векторное пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства 3 Связанные определения и свойства … Википедия

БАЗИС — множества X минимальное порождающее его подмножество В. Порождение означает, что применением операций нек рого класса к элементам получается любой элемент Это понятие связано с понятием зависимости: элементы Xпосредством операций из ставятся в… … Математическая энциклопедия

Базис — У этого термина существуют и другие значения, см. Базис (значения). Базис (др. греч. βασις, основа) множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде… … Википедия

Дуальный базис — Тензор объект линейной алгебры. Частными случаями тензоров являются скаляры, векторы и билинейные формы. Часто тензор представляют как многомерную таблицу (где d размерность векторного пространства, над которым задан тензор, а число… … Википедия

ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ — линейной однородной системы обыкновенных дифференциальных уравнений базис векторного пространства действительных (комплексных) решений этой системы. (Система может состоять и из одного уравнения.) Более подробно это определение формулируется… … Математическая энциклопедия

Пространство — (мат) [space] множество, между элементами которого определены некоторые соотношения, аналогичные обычным пространственным соотношениям. Множество всех n мерных точек составляет n мерное прoстранство Rn. Например, точки M (2; 8; 24) и N ( 4;6;… … Экономико-математический словарь

Источник

1.8.4. Базис и система координат пространства

Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.

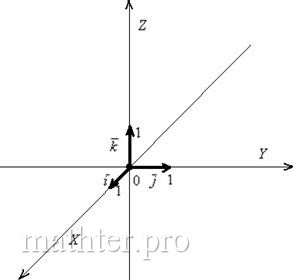
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.

И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец. Это будут векторы 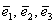, они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов!

Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)

Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными, и совершенно понятно, что базиса трёхмерного пространства они не создают.

Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).

Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.

Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (почему?).

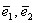
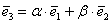
Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга.

И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.

Определение: базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов, взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в этом базисе. Также говорят, что вектор представлен в виде линейной комбинации базисных векторов.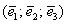

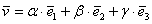
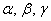
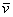
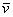
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки (начала отсчёта) и любых трёх линейно независимых векторов:

Выбранное (где угодно) начало координат , и некомпланарные векторы , взятые в определённом порядке, задают аффинную систему координаттрёхмерного пространства:

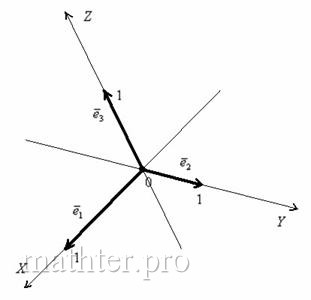
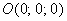
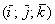
Наиболее привычным и удобным частным случаем аффинной системы координаявляется «школьная» система. Начало координат и ортонормированный базис задают декартову прямоугольную систему координат пространства:

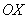
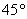
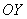
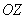
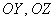
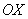
Ось абсцисс изображают под углом в по отношению к другим осям (к оси ординат и оси аппликат ). Популярный «тетрадный» масштаб: 1 ед. = 2 клетки по осям и 1 ед. = диагональ одной клетки – по оси .

И перед тем как перейти к практическим заданиям, вновь систематизируем теоретическую информацию:

Для трёх векторов пространства эквиваленты следующие утверждения:

1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.

Противоположные высказывания, думаю, понятны.

Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5), и оставшиеся практические задания параграфа будут носить ярко выраженный алгебраический характер. Повесим на гвоздь геометрическую клюшку и начнём орудовать бейсбольной битой линейной алгебры:

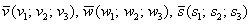
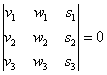
Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: .

Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (результат не изменится). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.

Задача 42

Проверить, образуют ли векторы базис трёхмерного пространства:

а)

б)

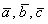
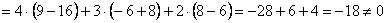
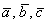
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):

, значит, векторы линейно независимы (не компланарны) и образуют базис трёхмерного пространства.

Ответ: данные векторы образуют базис.

б) Это пункт для самостоятельного решения. Не пропускаем! Для проверки правильности вычислений определителей я приложил к книге Алгебраический Калькулятор.

Решим творческую задачку:

Задача 43

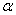
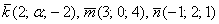
При каком значении параметра векторы будут компланарны?

Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:

По существу, требуется решить уравнение с определителем. Определитель выгоднее всего раскрыть по второй строке:

Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:

Ответ: при

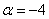
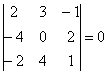
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново.

И в заключение параграфа рассмотрим ещё одну типовую задачу, которая встречается в подавляющем большинстве контрольных работ по алгебре и геометрии:

Задача 44

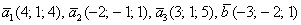
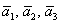
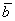
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.

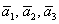
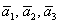
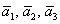
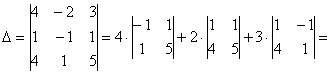
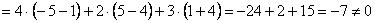
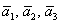
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать свой базис. И первый этап полностью совпадает с решением Задачи 42 – необходимо проверить, действительно ли векторы линейно независимы. Для этого нужно вычислить определитель, составленный из координат векторов :

, значит, векторы линейно независимы и образуют базис трехмерного пространства.

! Важно: координаты векторов 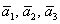обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.

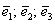
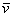
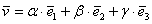
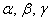
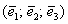
Теперь вспомним теоретическую часть: если векторы образуют базис, то любой вектор можно единственным способом разложить по данному базису: , где – координаты вектора в базисе .

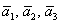
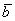
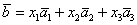
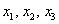
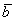
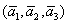
Поскольку наши векторы образуют базис трёхмерного пространства (это уже доказано), то вектор можно единственным образом разложить по данному базису:
, где – координаты вектора в базисе .

И по условию требуется найти координаты .

Для удобства объяснения поменяю части местами: . В целях нахождения следует расписать данное равенство покоординатно:
– коэффициенты левой части берём из опр-ля ,
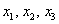
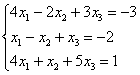
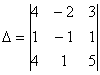
в правую часть записываем координаты вектора .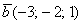

Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование.

Главный определитель системы уже найден: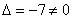
, значит, система имеет единственное решение.

Дальнейшее дело техники: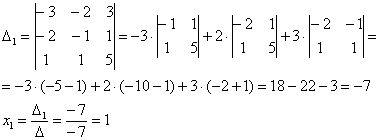

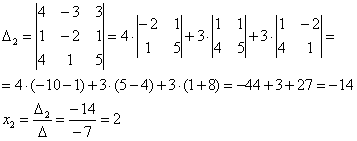
и ещё один определитель:

Таким образом:
– разложение вектора по базису .

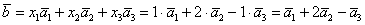
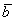
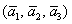
Ответ:

Такая же задача для самостоятельного решения:

Задача 45

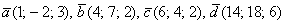
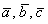
Даны векторы . Показать, что векторы образуют базис и найти координаты вектора в этом базисе. Систему линейных уравнений решить методом Крамера.

Полное решение и примерный образец чистового оформления в конце книги. Для самоконтроля используйте тот же Алгебраический Калькулятор, где есть макет с автоматическим расчётом системы по правилу Крамера.

Источник

Линейная Алгебра

Существование базиса векторного пространства.

Определение. Векторное пространство называется конечномерным, если оно обладает конечной порождающей системой векторов.

Замечание. Мы будем изучать только конечномерные векторные пространства. Несмотря на то, что мы уже довольно много знаем о базисе конечномерного векторного пространства, у нас нет уверенности, что базис такого пространства вообще существует. Все ранее полученные свойства были получены в предположении, что базис существует. Следующая теорема закрывает этот вопрос.

Теорема. (О существовании базиса конечномерного векторного пространства.)

Любое конечномерное векторное пространство обладает базисом.

Доказательство. По условию существует конечная порождающая система векторов данного конечномерного векторного пространства V: .

Мы можем считать, что все векторы этой системы ненулевые, ибо в противном случае, мы можем удалить их из этой системы и оставшаяся система векторов будет конечной порождающей системой.

Заметим сразу же, что если порождающая система векторов является пустой, т.е. не содержит ни одного вектора, то по определению полагают, что данное векторное пространство является нулевым, т.е. . В этом случае по определению полагают, что базисом нулевого векторного пространства является пустой базис и его размерность по определению полагают равной нулю.

Пусть далее, ненулевое векторное пространство и система ненулевых векторов является его конечной порождающей системой.

Если эта система линейно независимая, то все доказано, т.к. линейно независимая и порождающая система векторов векторного пространства является его базисом.

Если же данная система векторов является линейно зависимой, то один из векторов этой системы линейно выражается через оставшиеся и его можно удалить из системы, причем оставшаяся система векторов, будет по-прежнему порождающей.

Перенумеруем оставшуюся систему векторов: . Далее рассуждения повторяются.

Если эта система линейно независимая, то она является базисом. Если же нет, то снова найдется вектор в этой системе, который можно удалить, а оставшаяся система будет порождающей.

Повторяя этот процесс, мы не можем остаться с пустой системой векторов, т.к. в самом крайнем случае мы придем к порождающей системе из одного ненулевого вектора, которая является линейно независимой, а, следовательно, базисом. Поэтому, на каком-то шаге мы приходим к линейно независимой и порождающей системе векторов, т.е. к базису, ч.т.д.

Лемма. (О системах векторов в n-мерном векторном пространстве.)

Пусть . Тогда:

1. Любая система из вектора является линейно зависимой.

2. Любая линейно независимая система из векторов является его базисом.

Доказательство. 1). По условию леммы, число векторов в базисе равно и базис является порождающей системой, поэтому число векторов в любой линейно независимой системе не может превосходить , т.е. любая система содержащая вектор является линейно зависимой.

2). Как следует из только что доказанного, любая линейно независимая система из векторов этого векторного пространства является максимальной, а следовательно, базисом.

Теорема (О дополнении до базиса.) Любая линейно независимая система векторов векторного пространства может быть дополнена до базиса этого пространства.

Доказательство. Пусть векторное пространство размерности n и некоторая линейно независимая система его векторов. Тогда .

Если , то по предыдущей лемме, эта система является базисом и доказывать нечего.

Если же , тогда данная система является не максимальной линейной независимой системой (иначе она была бы базисом, что невозможно, т.к. ). Следовательно, найдется вектор , такой, что система – линейно независимая.

Если, теперь , то система является базисом.

Если же , все повторяется. Процесс пополнения системы не может продолжаться бесконечно, т.к. на каждом шаге мы получаем линейно независимую систему векторов пространства , а по предыдущей лемме число векторов в такой системе не может превышать размерности пространства. Следовательно, на каком-то шаге мы придем к базису данного пространства.