Что такое базисная форма

базисная форма

Смотреть что такое «базисная форма» в других словарях:

Базисная сеть — система треугольников, используемая в геодезических измерениях и обеспечивающая переход с требуемой точностью от непосредственно измеренного на местности короткого базиса геодезического (См. Базис геодезический) к более длинной (исходной) … Большая советская энциклопедия

ГОСТ 25634-83: Каталог координат геодезических пунктов. Форма и содержание — Терминология ГОСТ 25634 83: Каталог координат геодезических пунктов. Форма и содержание оригинал документа: 1.1. Общие сведения 1.1.1. В каталоге помещены координаты геодезических пунктов, определенных в 1933 1968 гг. Плановые координаты x, у… … Словарь-справочник терминов нормативно-технической документации

Формы организации обучения — Философская категория формы используется для описания способа упорядочивания объекта, его внутренней и внешней организации. Форма организации обучения это способ упорядочивания взаимодействия участников обучения, способ его существования. В … Википедия

ИНДУСТРИАЛЬНОЕ ОБЩЕСТВО — (industrial society) 1. Форма общества или какое либо определенное общество, в котором произошли индустриализация и модернизация. Термин принадлежит Сен Симону, выбравшему его для отражения усиливающейся роли обрабатывающей промышленности в… … Большой толковый социологический словарь

трехдольник — ТРЕХДО´ЛЬНИК одна из четырех элементных групп, участвующих в формировании правильных ритмических процессов стиха; он является малой метрической мерой стиха. В зависимости от объема анакрузы и эпикрузы Т. имеет три вида: Трехдольник 1 й | ⌣⌣⌣ |… … Поэтический словарь

НАЦИОНАЛЬНОГО ХАРАКТЕРА КОНЦЕПЦИИ — основаны на понятии “нац. характера”, обычно используемого для описания устойчивых личностных особенностей, характерных для членов той или иной нац. (или этнич.) группы; при этом исследуются доминирующие в группе паттерны внешнего… … Энциклопедия культурологии

Инсульт — I Инсульт Инсульт (позднелат. insultus приступ) острое нарушение мозгового кровообращения, вызывающее развитие стойкой (сохраняющейся более 24 ч) очаговой неврологической симптоматики. Во время И. происходят сложные метаболические и… … Медицинская энциклопедия

Вирусные гепатиты: симптомы, пути заражения, лечение и профилактика — Вирусные гепатиты распространенные и опасные инфекционные заболевания печени. Из всех форм вирусных гепатитов гепатит А является наиболее распространенным. От момента заражения до появления первых признаков болезни проходит от 7 до 50 дней. Чаще… … Энциклопедия ньюсмейкеров

Вирусные гепатиты: симптомы, пути заражения, методы лечения — Вирусные гепатиты распространенные и опасные инфекционные заболевания печени. Из всех форм вирусных гепатитов гепатит А является наиболее распространенным. От момента заражения до появления первых признаков болезни проходит от 7 до 50 дней. Чаще… … Энциклопедия ньюсмейкеров

Фирма — (Firm) Определение фирмы, признаки и классификация фирм Определение фирмы, признаки и классификация фирм, концепции фирмы Содержание Содержание Фирма Юридические формы Понятие фирмы и предпринимательства. Основные признаки и классификации фирм… … Энциклопедия инвестора

Источник

Подробный разбор симплекс-метода

Пролог

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

Замечание: ≥0.

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение: Пусть есть система m уравнений и n неизвестных (m

Источник

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показать\скрыть

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Если система является неопределённой, указать базисное решение.

Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.

Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

СЛАУ решение в базисной форме

Последний раз редактировалось Limit79 31.10.2012, 00:10, всего редактировалось 1 раз.

Что значит представить решение СЛАУ в базисной форме?

В смысле как оно должно выглядеть?

Есть некоторая слау, я получил ее решение, где базисные переменные выражены через свободные, а как быть дальше?

Я понимаю как «найти какое-либо базисное решение системы уравнений», или это одно и тоже с моим вопросом?

Заслуженный участник

Последний раз редактировалось Limit79 31.10.2012, 00:45, всего редактировалось 2 раз(а).

Методом Гаусса решить систему и представить ее решение в базисной форме:

А во втором задании такая же размерность системы и задание, но она однородная.

В этом случае выражаем свободные переменные через базисные, потом придаем свободным переменным нулевые значения, и вычисляем значения базисных переменных, это и будет базисное решение.

Одинаковы? (касательно базисного решения).

Решение получилось вот такое:

Может таки кто-нибудь знает, как представить это решение в базисной форме?

Весь интернет перерыл, нигде не нашел такой формулировки.

Незачем вводить лишнюю постоянную.

У вас есть 4 уравнения, 5 неизвестных, значит как минимум одна из них будет произвольной, то есть решений у вас бесчисленное множество (действительно все переменные окажутся выраженными через несколько свободных). Множество этих решений образуют линейное пространство, можете это проверить (понятно как)? Далее вас просят найти базис в этом пространстве, просто воспользуйтесь определением базиса.

Параграф 0.3, там то, что вы называете базисным решением называют частным. Более подробно с объяснением смысла всего этого смотреть в параграфе 3.5. Примеров разобрано много.

Последний раз редактировалось Limit79 01.11.2012, 22:10, всего редактировалось 3 раз(а).

still alive
Т.е. надо придать свободным переменным нулевые значения, и найти базисные, исходя из этого?

Там придают свободным переменным значения , и . А мне получается надо придать только значение ?

И базис будет: ?

Или все таки ответ будет вот такой:

Последний раз редактировалось Limit79 01.11.2012, 23:18, всего редактировалось 1 раз.

still alive
Все равно не очень понял.

Мы же имеем бесконечно много решений, и надо представить эти решения в базисной форме, то есть, как я думаю, будет вот так:

Где — произвольная константа, так как решений бесконечно много.

А если, обнулить , или же придать , то мы же получим частное решение?

А не множество ли линейных пространств?

Хоть может чушь сказал.

Последний раз редактировалось still alive 01.11.2012, 23:22, всего редактировалось 2 раз(а).

Нет. Решений бесконечно много, вы их представляете выражая переменных через свободных переменных. Никаких произвольных постоянных не может здесь возникать, если конечно они не заданы в условии задачи.

Множество решений образуют линейное пространство и вы ищете его базис, размерность пространства решений равна числу свободных переменных, в вашем случае она одна. Вы приравниваете свободную переменную к единице и получаете один базисный вектор. Через него можно представить любое решение вашей системы. Для примера возьмите и приравняйте свободную переменную двум, получите ещё один вектор который сможете линейно выразить через ваш базисный простым домножением на двойку.

Просто аккуратно разберитесь с определениями которые используете, например про базис линейного пространства и то какую информацию он даёт. Ну а алгоритм решения задачи вам уже известен, по той ссылке которую вы дали он неплохо изложен.

Это делается так. Сомневаетесь — берёте определение линейного пространства, берёте объект который вас интересует и начинаете проверять удовлетворяет ли объект определению.

Последний раз редактировалось Limit79 01.11.2012, 23:26, всего редактировалось 1 раз.

Вы пишите:

Хотя могли бы этого не делать и сразу выражать все значения через , если вам так нравится вводить новые переменные наверное можно и так, только не совсем логично называть это константой, потому что у вас здесь все величины переменные, даже свободные.

Два вектора у вас не будет, векторов у вас должно быть столько сколько свободных переменных в уравнении, здесь она одна, вектор будет один, выше вы написали сумму двух векторов это по-сути один вектор.

Заслуженный участник

Последний раз редактировалось gris 02.11.2012, 11:26, всего редактировалось 3 раз(а).

Заслуженный участник

Заслуженный участник

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник

Системы уравнений в базисной форме.

Рассмотрим произвольную систему

(16.1)

когда .

Для нахождения общего метода исследования и решения такой системы введем в рассмотрение ее частный случай. Система вида

(16.2)

называется системой в базисной форме.

Неизвестные называются свободными, а — несвободными или базисными неизвестными. Выбор базисных и свободных переменных может быть различным в общем случае.

Система (16.1) имеет решение в том и только том случае, когда ее можно записать в базисной форме.

Перенесем все свободные неизвестные в правые части уравнений системы (16.2). Тогда получим

(16.3)

Если свободным неизвестным придать конкретные числовые значения, то по формулам (16.3) можно вычислить базисные неизвестные. Таким образом, базисная система (16.2) всегда имеет решение. Причем возможны следующие варианты.

и является определенной, так как имеет единственное, очевидное решение. Матрицей такой системы является единичная матрица

.

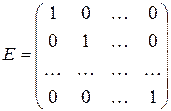
2). m

Источник