Что такое базисные функции

Базисная функция

Наборы базисных функций обладают тем свойством, что все функции из данного функционального пространства (с учётом некоторых ограничений) могут быть представлены как их линейная комбинация. Например, любая аналитическая функция одного аргумента может быть разложена в сумму степенных функций с различными коэффициентами, то есть разложена в ряд Тейлора. Если в качестве базисных выбраны синусоидальные функции, то разложение по ним есть преобразование Фурье и т. д.

Связанные понятия

Кэлеровы дифференциалы представляют собой адаптацию дифференциальных форм для произвольных коммутативных колец или схем. Это понятие было введено Эрихом Кэлером в 1930-х.

В математике и теоретической физике функциональная производная является обобщением производной по направлению. Разница заключается в том, что для последней дифференцирование производится в направлении какого-нибудь вектора, а для первой речь идёт о функции. Оба эти понятия можно рассматривать как обобщение обычного дифференциального исчисления.

К вейвлет-функциям с компактным носителем относятся вейвлеты Добеши, койфлеты и симмлеты. Метод построения вейвлет-функций с компактным носителем принадлежит Ингрид Добеши. Койфлеты являются частным случаем вейвлетов Добеши с нулевыми моментами скейлинг-функции.

Сглаживающие операторы — это гладкие функции со специальными свойствами, используемые в теории распределений для построения последовательности гладких функций, приближающей негладкую (обобщённую) функцию с помощью свёртки. Интуитивно, имея функцию с особенностями и осуществляя её свёртку со сглаживающей функцией, получаем «сглаженную функцию», в которой особенности исходной функции сглажены, хотя функция остаётся близкой к исходной функции. Операторы известны также как сглаживающие операторы Фридрихса.

Квазианалити́ческие фу́нкции в математическом анализе — класс функций, которые, нестрого говоря, можно полностью реконструировать по их значениям на небольшом участке (например, на границе области). Такое свойство значительно облегчает решение дифференциальных уравнений и исследование других задач анализа. Поскольку это свойство выполняется для аналитических функций (см. Комплексный анализ), то класс квазианалитических функций содержит класс обычных аналитических функций и может рассматриваться как.

В теории категорий есте́ственное преобразова́ние предоставляет способ перевести один функтор в другой, сохраняя внутреннюю структуру (например, композиции морфизмов). Поэтому естественное преобразование можно понимать как «морфизм функторов». Эта интуиция может быть строго формализована в определении категории функторов. Естественные преобразования — наиболее базовое определение в теории категорий наряду с функторами, поэтому оно появляется в большинстве её приложений.

Антиголоморфные функции (также называемые антианалитическими) — семейство функций, тесно связанных с голоморфными функциями.

В этой статье рассматривается математический базис общей теории относительности.

Смешанные частные производные одной и той же функции, отличающиеся лишь порядком (очерёдностью) дифференцирования, равны между собой при условии их непрерывности. Такое свойство называется равенством смешанных производных.

Источник

Системы базисных функций

В общем виде любой сигнал может быть представлен в виде ряда:

, (1)

где j _k (t) – представляет собой единичные орты, а а_к – проекции функций на соответствующие оси или спектральные коэффициенты, которые определяются по формуле

. (2)

СБФ должна удовлетворять условиям ортогональности и ортонормированности.

Условия ортогональности двух базисных функций заключаются в равенстве нулю их взаимных мощностей

. (3)

Условия ортонормированности заключаются в равенстве единице мощности всех базисных функций

(4)

Любую СБФ можно нормировать, если разделить каждую базисную функцию на ее мощность.

Существует бесконечное множество СБФ, при этом различным СБФ соответствует различная физическая интерпретация сигнала, а значит и практическая реализация. Выбор СБФ зависит от специфики решаемой задачи (например: анализ фильтров, оценка точности, быстродействия и т.д.), используемых методов (временные, частотные, операторные и т.д.) и других факторов.

Наиболее часто используются следующие СБФ:

– Системы единичных непрерывных и дискретных функций.

– Системы тригонометрических базисных функций:

.

Эти функции широко используются при частотном представлении сигналов в рядах Фурье.

– Системы комплексных экспоненциальных функций- . Эти функции используются в преобразованиях Фурье и Лапласа.

– Системы комплексных дискретных экспоненциальных, базисных функций- . Эти функции используются в дискретных преобразованиях Фурье и Лапласа, быстром преобразовании Фурье.

– Полиномиальные СБФ, использующие полиномы Чебышева и Лежандра. Эти функции часто используются для анализа и синтеза цифровых фильтров.

– Двоично – ортогональные СБФ Уолша, Хаара, Радемахера. Эти функции широко используются в вычислительной технике для анализа и синтеза цифровых автоматов.

Базисные функции составляют ядро различных интегральных преобразований, используемых для исследования сигналов и систем (Фурье, Лапласа, Карсона, Хэвисайда, Уолша, Хаара и др.), которые имеют следующую структуру записи:

, . (5)

При этом, различным СБФ соответствует различная интерпретация сигналов.

1. Ряд Фурье и интегральное преобразование Фурье

Любая периодическая функция, удовлетворяющая условиям Дирихле (ограниченная, кусочно-непрерывная и имеющая на протяжении периода конечное число экстремумов), может быть разложена в ряд Фурье:

,

где – постоянная составляющая функции f(t);

– круговая частота основной (первой) гармоники;

– частота первой гармоники;

— амплитуда, частота и начальная фаза к – той гармоники;

;

; ;

; .

Ряд Фурье можно представить в комплексной форме:

; . (6)

Пример 1. Дана периодическая последовательность импульсов, приведенная на рис. 1. Найти сумму ряда.

f(t)

Рис. 1. Периодическая последовательность импульсов

Определим выражение для спектральных коэффициентов

.

Периодическую последовательность импульсов можно представить в виде суммы ряда:

.

Интеграл Фурье

Для апериодических процессов вместо разложения в ряд Фурье используется разложение в интеграл Фурье при выполнении следующих условий: функция f(t) удовлетворяет условиям Дирихле и является абсолютно интегрируемой т.е.

. (7)

Формулы прямого и обратного преобразования Фурье имеют вид:

, . (8)

Пример 2. Определим спектральную плотность для одиночного прямоугольного импульса, приведенного на рис. 2.

0 t

Рис. 2. Одиночный прямоугольный импульс

Одиночный прямоугольный импульс может быть представлен следующим выражением:

.

Спектральная плотность для одиночного прямоугольного импульса имеет вид:

Пример Определим спектральную плотность низкочастотного шума корреляционная функция которого имеет вид:

Спектральная плотность при этом равна:

Проверка: Выполним обратное преобразование

Определим оригинал как сумму вычетов по полюсам подынтегральной функции

,

где s_k – значения полюсов; n – количество полюсов; m – кратность полюсов.

При этом, корреляционная функция равна

2. Дискретное преобразование Фурье

В цифровой технике для обработки дискретной информации широко используются ряды Фурье и дискретное преобразование Фурье. При этом, используются комплексные экспоненциальные СБФ, для которых характерны свойства ортогональности, ортонормированности, полноты и мультипликативности

, при k = m+n. (9)

Ряд Фурье может быть представлен в виде

(10)

(15)

При реализации алгоритмов вычисления ДПФ необходимо учитывать количество выполняемых арифметических операций и их тип (умножение, сложение и т.д.), процедуры обращения к памяти и ее объем для хранения коэффициентов. В дискретном преобразовании Фурье необходимо выполнить N 2 умножений и N 2 сложений.

При этом, для вычисления спектральных коэффициентов требуются одни и те же промежуточные спектры, что существенно сокращает объем вычислений. В некоторых случаях оказывается удобная БПФ с прореживанием по времени, в других случаях по частоте.

.

Решение: Алгоритм решения задачи можно представить в виде

.

1. Для заданной спектральной плотности определим корреляционную функцию

2. Определим дискретную корреляционную функцию

Определим дискретную спектральную плотность

Проверка: Определим дискретную корреляционную функцию

Используя теорему Коши о вычетах, корреляционную функцию можно определить как сумму вычетов по полюсам подынтегральной функции

Так как корреляционная функция является четной, то ее можно представить в виде

При реализации алгоритмов БПФ возможно распараллеливание вычислений (специализированные процессоры), что позволяет ускорить выполнение преобразований.

Области применения дискретного преобразования Фурье:

дискретный спектральный анализ;

моделирование цифровых фильтров;

дискретный анализ речевых сигналов;

исследование дискретных систем управления.

Список использованной литературы

1.Шеннон К. Математическая теория связи. – В сб. «Работы по теории информации и кибернетике». М., «Иностранная литература», 1963.

2.Фано К. Передача информации. Статистическая теория связи. М., «Мир», 1965.

3.Балюкевич Э.Л. Элементы теории кодирования. М., МЭСИ, 1976.

4.Стратонович Р.Л. Теория информации. М., «Советское радио», 1975.

5.Лапа В.Г. Математические основы кибернетики. Киев, «Вища школа», 1974.

6.Гринченко А.Г. Теория информации и кодирование: Учебн. пособие. –Харьков: ХПУ, 2000.

7.Цымбал В.П. Теория информации и кодирование. – М.: Высш. шк., 1986.

Источник

Базисная функция

Базисная функция — функция, которая является базисным вектором, если совокупность всевозможных функций представлять как линейное пространство.

Наборы базисных функций обладают тем свойством, что все остальные функции (с учётом некоторых ограничений) могут быть разложены на их сумму (или интеграл). Например, любая аналитическая функция одного аргумента может быть разложена в сумму степенных функций с различными коэффициентами, то есть разложена в ряд Тейлора. Если в качестве базисных выбраны синусоидальные функции, то разложение по ним есть преобразование Фурье и т. д.

Полезное

Смотреть что такое «Базисная функция» в других словарях:

Искусственный нейрон — Схема искусственного нейрона 1.Нейроны, выходные сигналы которых поступают на вход данному 2.Сумматор входных сигналов 3.Вычислитель передаточной функции 4.Нейроны, на входы которых … Википедия

Метод опорных векторов — Запрос «SVM» перенаправляется сюда; см. также другие значения. Метод опорных векторов (англ. SVM, support vector machine) набор схожих алгоритмов вида «обучение с учителем», использующихся для задач классификации и регрессионного… … Википедия

SVM — Метод опорных векторов (SVM support vector machines) – это набор схожих алгоритмов вида «обучение с учителем», использующихся для задач классификации и регрессионного анализа. Этот метод принадлежит к семейству линейных классификаторов. Он может… … Википедия

Support vector machine — Метод опорных векторов (SVM support vector machines) – это набор схожих алгоритмов вида «обучение с учителем», использующихся для задач классификации и регрессионного анализа. Этот метод принадлежит к семейству линейных классификаторов. Он может… … Википедия

Support vector machines — Метод опорных векторов (SVM support vector machines) – это набор схожих алгоритмов вида «обучение с учителем», использующихся для задач классификации и регрессионного анализа. Этот метод принадлежит к семейству линейных классификаторов. Он может… … Википедия

Машина опорных векторов — Метод опорных векторов (SVM support vector machines) – это набор схожих алгоритмов вида «обучение с учителем», использующихся для задач классификации и регрессионного анализа. Этот метод принадлежит к семейству линейных классификаторов. Он может… … Википедия

Сравнение алгоритмов выделения лиц — Содержание 1 Аннотация 2 Введение 2.1 Методы, основанные на знаниях … Википедия

B-сплайн — В вычислительной математике B сплайном называют сплайн функцию, имеющую наименьший носитель для заданной степени, порядка гладкости и разбиения области определения. Фундаментальная теорема устанавливает, что любая сплайн функция для заданной… … Википедия

СКРЫТАЯ ПРОГРАММА — (hidden system) совокупность ценностей, позиций, знаний, реализуемая в организации и процессах обучения и прививаемая ученикам в неявной форме. Все школы имеют формальную программу, состоящую из элементов академического знания, которое ученики,… … Большой толковый социологический словарь

РИЗОМА — (фр. rhizome корневище) понятие философии постмодерна, фиксирующее принципиально внеструктурный и нелинейный способ организации целостности, оставляющий открытой возможность для имманентной автохтонной подвижности и, соответственно, реализации ее … История Философии: Энциклопедия

Источник

Системы базисных функций (СБФ)

Один и тот же сигнал может быть разложен по различным СБФ или, что одно и то же, рассмотрен в различных системах координат. При этом внутренние закономерности сигналов не могут нарушаться при изменении системы координат. Однако спектральному анализу в различных СБФ соответствует различная физическая интерпретация и, что особенно важно, различная практическая реализация. При решении практических задач целесообразно подбирать наиболее подходящие СБФ. Выбор базиса во многом обусловлен спецификой решаемых задач и требованиями, предъявляемыми при их решении.

Если задан ряд из N чисел X₁, X₂, …, X_k,…, X_N,(1) то и функциональный базис следует выбрать из конечного набора N функций Ф_a (Х), a = 1, 2,…, N,(2) существующих на совокупности точек X_k. Тогда дискретное преобразование в этом базисе даст ровно N коэффициентов C_a, кoтoрыe находятся с помощью формального суммирования: C_a = S_k X_k Ф_a (X_k), a = 1, 2,…, N. (3) Совокупность N коэффициентов C_a и составляет дискретное представление ряда чисел (1) в функциoнaльном базисе (2). Часто эту совокупность чисел C_a называют линейчатым спектром в выбранном базисе.

Полных и ортогональных СБФ существует бесчисленное множество.

(3.17)

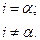
Такая система определена на целочисленном интервале [0, N). Система <u_(i)> в форме (3.17) является ненормированной, и ее норма (корень квадратный из мощности) Эта система представляет собой полную СБФ, служащую для разложения дискретных сигналов произвольной формы. Система дискретных единичных функций обладает тем свойством, что ее спектральный коэффициент с номером  совпадает со значением сигнала в точке i =  его интервала определения, т.е. c_a = x().

Полиномиальные базисные системы. К ним относят системы, построенные на основе ортогональных полиномов.

Двоично-ортогональные системы базисных функций. Под этим условным названием объединены системы функций меандрового типа Радемахера, Уолша и Хаара, интервал ортогональности которых при их построении представляется совокупностью двоично-рационального числа равных подынтервалов. Эти системы имеют важное значение для практики спектральной обработки, поскольку принимают только значения 1 (функция Радемахера и Уолша) либо 1 и 0 (функция Хаара) и легко могут быть получены с помощью цифровых устройств. Все эти системы взаимосвязаны друг с другом и каждую из них можно получить из другой, образуя соответствующую линейную комбинацию.

Функции Уолша

Функции Уолша различают по их порядку и рангу. Под порядком понимают максимальный из содержащих единицу номеров разрядов при двоичном представлении числа n, рангом называют число единиц в двоичном выражении n. Например, порядок и ранг функции wal(5,) равны соответственно 3 и 2, так как двоичным выражением числа 5 является 101. Функции Уолша могут быть упорядочены по Уолшу. Имеется упорядочивание функций Уолша по Пэли.

Система Уолша-Пэли. Масштабирование данных.

Во многих автоматизированных устройствах используются табличные данные. Одним из методов может быть метод сжатия табличной информации за счет ее спектрального разложения в некотором функциональном базисе. Более выгодным является использование для разложения базиса Уолша, так как для гладких функций коэффициенты разложения Уолша быстрее стремятся к нулю. Это допускает большую степень сжатия информации в базисе Уолша. Возможность сжатия информ. появляется, если число коэффициентов спектра можно сделать меньше числа N. Например, когда часть коэффициентов спектра равна нулю или близка к нему. Возможность сжатия информации и степень ее сжатия зависят как от самого ряда чисел, так и от набора функций, составляющих базис спектрального разложения C_a. Поскольку ряд чисел Х_k нам задан, то управлять степенью сжатия мы можем, изменяя базис спектрального разложения.

Именно это важное неравенство гарантирует быструю сходимость спектральных коэффициентов C_a с ростом номера a и открывает перспективы сжатия табличной информации. Действительно, ранг r функции Уолша увеличивается с ростом номера функции a так, что условие r ³ m выполняется для больших номеров a. Это значит, что оценка действует для финальных коэффициентов разложения. Чем меньше степень функции, которая порождает ряд чисел (l), тем большей степени сжатия можно достичь при разложении. Если ряд короткий, а степень велика, то сжатие вообще не достигается. Если при той же степени функции увеличивать число членов ряда и, следовательно, число коэффициентов спектра, то степень сжатия растет.

6.Классификация информационных сигналов. Сигналы. Модели процессов, аналитически представляющих сигнал. Аналитическое описание сигналов.

Результаты обработки информации существенно зависят от выбора рациональной модели анализируемого сигнала.

Обычно в качестве детерминированных моделей используются следующие элементарные колебания: -импульс, функция включения (скачок) s(t)=1(t), треугольный импульс, гармонические функции sin(t), cos(t), отрезок гармонической функции, экспоненциальная функция exp(t), комплексно-экспоненциальная функция exp(jt), функция sin(t)/t и другие. Детерминированные модели сигналов более сложного вида могут быть сформированы из элементарных путем линейных комбинаций.

Сигнал называется каузальным, если он имеет начало во времени. Все реальные сигналы являются каузальными.

Сигнал называется периодическим, если любое его значение повторяется через интервалы, равные периоду. Финитным называется сигнал, равный нулю вне некоторого ограниченного интервала его определения. Все реальные сигналы могут рассматриваться как финитные.

В зависимости от формы представления сигналы могут быть непрерывными, квантованными по уровню, дискретными и цифровыми

Формы представления сигнала

Множество значений	Наименование	Изображение
времени	сигнала
Непрерывное	Непрерывное	Непрерывный (аналоговый, континуальный)
Непрерывное	Дискретное	Квантованный по уровню (ступенчатая функция)
Дискретное	Непрерывное	Дискретный (решетчатая функция, последовательность вещественных чисел)
Дискретное	Дискретное	Цифровой (последовательность целых чисел

По характеру протекания во времени сигналы разделяются на два вида:

Сигнал называется случайным, если его значение в каждый момент времени есть случайная величина.

Случайные сигналы делятся на: стационарные и нестационарные. У стационарных сигналов вероятностные характеристики не зависят от времени (постоянны). Стационарные сигналы, для которых вероятностные характеристики не зависят от способа усреднения (по времени и ансамблю) называются эргодическими.

Все случайные сигналы в итоге классифицируются по виду закона распределения плотности вероятности, который является полной и исчерпывающей характеристикой любого случайного сигнала.

Источник