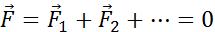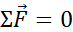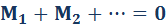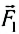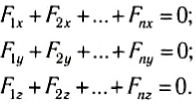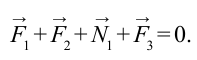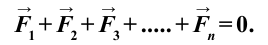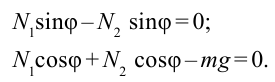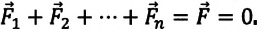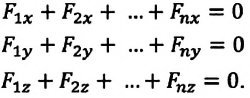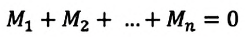Что такое безразличное равновесие

Равновесие тел. Виды равновесия тел

Виды равновесия тел

Это происходит, если при небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. Например, шарик, лежащий на дне сферического углубления (рис.1 а).

В данном случае при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Примером может служить шарик, находящийся в верхней точке выпуклой сферической поверхности (ри.1 б).

В этом случае при небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю. Например, шарик, лежащий на плоской поверхности (рис.1,в).

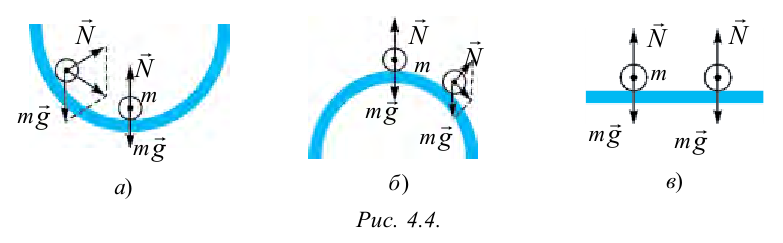
Рис.1. Различные типы равновесия тела на опоре: а) устойчивое равновесие; б) неустойчивое равновесие; в) безразличное равновесие.

Статическое и динамическое равновесие тел

Если в результате действия сил тело не получает ускорения, оно может находиться в состоянии покоя или двигаться равномерно прямолинейно. Поэтому можно говорить о статическом и динамическом равновесии.

Динамическое равновесие — это такое равновесие, когда по действием сил тело не изменяет своего движения.

В состоянии статического равновесия находится подвешенный на тросах фонарь, любое строительное сооружение. В качестве примера динамического равновесия можно рассматривать колесо, которое катится по плоской поверхности при отсутствии сил трения.

Источник

Условия равновесия тел

Статикой называется раздел механики, изучающий условия равновесия тел.

Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.

или

Равновесие твердого тела под действием трех сил. При вычислении равнодействующей все силы приводятся к одной точке C

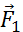
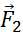
На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил и не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.

Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения.

Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.

Произведение модуля силы 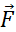на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).

Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

В Международной системе единиц (СИ) моменты сил измеряются в Ньютон—метрах (Н∙м).

Источник

Содержание:

Условия равновесия тел:

Основным признаком взаимодействия тел в динамике является возникновение ускорений. Однако часто бывает нужно знать, при каких условиях тело, на которое действует несколько сил, не движется с ускорением, а покоится или движется равномерно и прямолинейно. В последнем случае мы всегда можем выбрать другую инерциальную систему отсчета, в которой тело покоится, поэтому в дальнейшем будем изучать условия равновесия покоящихся тел.

Раздел механики, в котором изучаются условия равновесия тел, называется статикой.

Все опытные факты, которые мы рассмотрели в предыдущих параграфах, убеждают нас в том, что тело покоится, если равнодействующая всех сил, действующих на него, равна нулю.

Итак, первое условие равновесия тела: векторная сумма всех сил, приложенных к телу, равна нулю.
Если на тело действует n сил

Из этого условия следует, что и сумма проекций всех сил на любое направление тоже должна быть равна нулю. В частности, сумма проекций сил на оси выбранной декартовой системы координат равна нулю:

Фактически эти три равенства эквивалентны одному векторному равенству ( 1 ). Но с их помощью достаточно просто решать задачи, поскольку проекции сил — скалярные величины.

В повседневной жизни и технике часто встречаются тела, которые не могут двигаться поступательно, но могут вращаться вокруг оси. Примерами таких тел могут служить двери и окна, качели, колеса машин и детали механизмов и т. д.

На рисунке 149, а изображен однородный диск, который может вращаться вокруг закрепленной оси, проходящей через его центр — точку О. Если подвесить к нему тело в точке А, то диск будет находиться в равновесии.

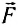
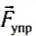
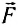
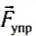
Естественно, что действующая сила будет уравновешиваться силой упругости со стороны оси вращения. Если подвесить тело в точке В, то равновесие тоже не нарушится. Отсюда можно сделать вывод, что точку приложения силы натяжения можно переносить вдоль линии действия силы. При этом силы и лежат на одной прямой.

Если же прямая, на которой лежит вектор силы 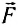, не проходит через ось вращения, то эта сила не может быть уравновешена силой упругости оси, и тело поворачивается вокруг нее (рис. 149, б).

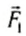
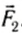
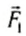
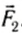
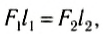
На рисунке 149, в изображен тот же диск, на который действуют две силы и . Численные значения этих сил определяются динамометрами. Сила вращает диск против часовой стрелки, а сила — по часовой стрелке. Диск не будет вращаться, если выполняется условие:
(2)

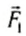
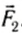
где l₁ и l₂ — кратчайшие расстояния от оси вращения до прямых, на которых лежат векторы сил и .

Итак, мы получили известное вам из курса физики 8-го класса условие равновесия рычага.

Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы, а произведение модуля силы F на плечо l называется моментом силы М:
M = Fl (3)

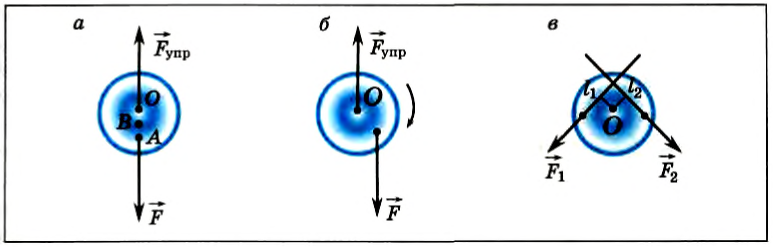
Рис. 149

Следовательно, равенство (2) означает равенство моментов сил F₁ и F₂. Но момент силы F₁ вращает диск против часовой стрелки, а момент силы F₂ — по часовой стрелке. Поэтому им нужно приписать различные знаки. Обычно положительным считают момент силы, вызывающий вращение по часовой стрелке, а отрицательным — момент силы, вызывающий вращение против часовой стрелки.

Итак, вторым условием равновесия тела является правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу, относительно этой оси равна нулю.

Таким образом, тело будет находиться в равновесии, если выполняются два условия: (1) и (4). Например, доска, изображенная на рисунке 150, находится в равновесии.

Рис. 150

Главные выводы:

Условия равновесия тел

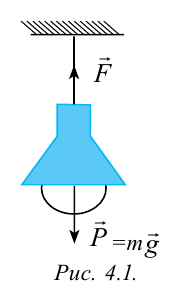
Рассмотрим силы, действующие на подвешенную к потолку лампу (рис. 4.1). Для начала вспомним изученное в 6-м классе понятие «центр масс» тела.

Центр масс – это воображаемая точка, в которой воплощена вся масса тела.
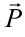
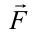
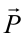
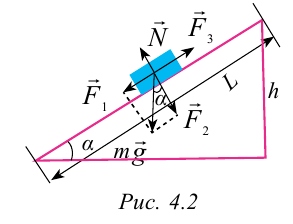
Исходя из этого будем считать, что силы, действующие на тело, приложены к центру масс. На подвешенную лампу действует направленная вниз сила тяжести . При этом туго натягивается удерживающая ее нить. Возникающая в нити сила натяжения и сила тяжести действуют вдоль одной прямой линии, которая проходит через центр массы и направлены противоположно. Эти силы равны по модулям. Если эти силы сложить по правилу сложения векторов, то результирующая сила становится равной нулю. Поэтому лампа остается в положении равновесия.

Рассмотрим случай, когда тело покоится в равновесии на наклонной плоскости (рис. 4.2). Рассмотрим действующие относительно центра масс силы в этом случае. На тело действует сила тяжести .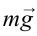
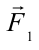
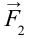
Эту силу разделим на составляющие: и .

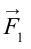
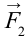
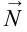
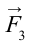
При этом сила стремится сдвинуть тело вниз по наклонной плоскости, сила представляет силу давления на площадь наклонной плоскости. Эта сила приводит к образованию силы реакции на тело со стороны наклонной плоскости. Также на тело действует сила трения в противоположном относительно скольжения направлении.

В этом случае векторная сумма всех действующих сил тоже будет равна нулю.

Исходя из вышесказанного можно сделать следующие выводы:
Для того чтобы тело или система тел, не имеющие вращения оси, остались в равновесии, векторная сумма всех действующих на них сил должна быть равна нулю.

Виды равновесия

Если некое тело находится в состоянии равновесия, это не означает, что оно постоянно будет находиться в таком состоянии (рис. 4.3). В реальных условиях тело подвергается неожиданным воздействиям извне, которые невозможно избежать. Главное, что нужно знать – останется ли тело после такого воздействия в равновесии или равновесие будет нарушено. Для этого необходимо учесть направление результирующей силы внешнего воздействия. В зависимости от направления результирующей силы различают три вида равновесия.

Устойчивое равновесие

При выведении тела из положения равновесия возникают силы, возвращающие тело в прежнее положение, это называется устойчивым равновесием (рис. 4.4а). В данном случае, при небольшом смещении шарика, лежащего на дне сферического углубления, равнодействующая сила возвращает его в положение равновесия.

Неустойчивое равновесие

При выведении тела из положения равновесия возникают силы, удаляющие его от положения равновесия, это называется неустойчивым равновесием (рис. 4.4б). В данном случае шарик находится в верхней точке выпуклой сферической поверхности. При небольшом смещении из положения равновесия равнодействующая сила действующих на него сил удаляет его еще дальше от состояния равновесия.

Безразличное равновесие

Равновесие, при котором смещение тела в любом направлении не вызывает изменения действующих на него сил и равновесие тела сохраняется, называется безразличным равновесием (рисунок 4.4в). Если приложить силу к шарику, находящемуся на горизонтальной поверхности, то он переместится на другое место.

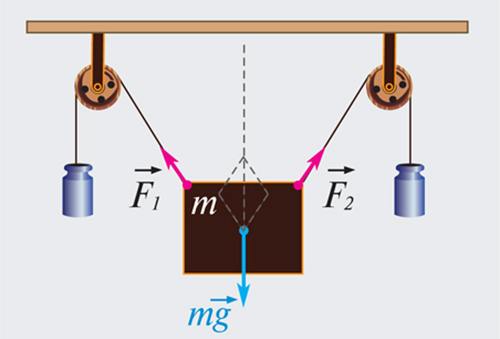
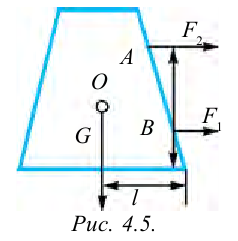
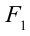
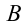
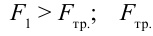
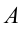
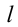
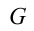
Если на тело, показанное на рисунке 4.5 действует сила в точке ниже центра тяжести ( – сила трения), тело приходит в поступательное движение. Не меняя величину силы, приложим ее к точке , при этом тело начинает наклоняться. Начинает уменьшаться расстояние между крайними точками нижнего основания контура и вектором, направленным вниз из центра тяжести. Если продолжить прикладывать силу, вектор выйдет за пределы контура тела и оно опрокинется.

Таким образом, равновесие тела зависит от:

Образец решения задачи

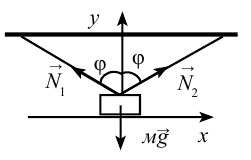
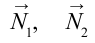
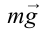
Согласно чертежу, действующие на груз силы и пересекаются в одной точке.
Следовательно, условие равновесия определяется двумя уравнениями:

После внесения математических изменений получим: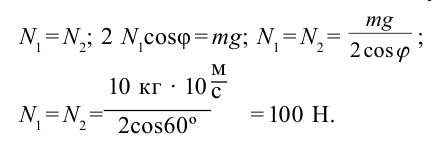

Ответ: 100 Н.

Определение условия равновесия тела

По I закону Ньютона, нахождение тела в состоянии равновесия означает, что оно находится в покое или движется прямолинейно и равномерно в инерциальной системе отсчета. Ознакомимся с условиями, при выполнении которых тело остается в состоянии равновесия.

Равновесие тела при поступательном движении

Для нахождения тела в состоянии равновесия при его поступательном движении равнодействующая сила (геометрическая сумма всех действующих на тело сил), прикладываемая к телу, должна быть равна нулю:

Если геометрическая сумма сил равна нулю, то и сумма проекций этих сил на произвольную координатную ось равна нулю:

Равновесие тела с неподвижной осью вращения

Тело с неподвижной осью вращения находится в равновесии, если алгебраическая сумма моментов действующих на него сил относительно оси вращения равна нулю:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Равновесие: определение, виды, примеры

Дата публикации: 26.10.2019 2019-10-26

Статья просмотрена: 8818 раз

Библиографическое описание:

Григорьев, К. А. Равновесие: определение, виды, примеры / К. А. Григорьев, А. А. Григорьев. — Текст : непосредственный // Юный ученый. — 2019. — № 9 (29). — С. 24-28. — URL: https://moluch.ru/young/archive/29/1761/ (дата обращения: 08.12.2021).

Изучение видов равновесия.

Рассмотреть виды равновесия.

Выявить их отличия друг от друга.

Показать практическое применение описанных эффектов.

Опытным путём рассчитать зависимость вероятности падения хлеба маслом вниз от соотношения толщин хлеба и масла.

В природе всё пребывает в равновесии, нет предметов, у которых не было бы центра тяжести и зачастую его сложно определить.

Основная часть

Самая главная наука во вселенной — это физика. На физике, как на фундаменте, стоят все прочие науки. Физика — многогранна и сегодня речь пойдёт о механическом равновесии и его видах.

4.1. Что такое равновесие

Что такое равновесие? Понятие равновесия — одно из самых универсальных в естественных науках.

Равновесие — это комплекс сил, которые действуя на одну систему, компенсируют друг друга и система не получает ускорение. А система— множество элементов, находящихся в отношениях и связях друг с другом, которое образует определённую целостность, единство.

4.2. Виды равновесия

Существует 3 вида равновесия: устойчивое, неустойчивое и безразличное.

Устойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, возвращается в прежнее положение.

Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.

Безразличное равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, не меняет своего положения (состояния).

1 опыт: устойчивое равновесие: шарик неподвижно лежит на дне сферического углубления. При небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. Шарик возвращается в исходную точку.

2 опыт: неустойчивое равновесие: шарик неподвижно лежит на вершине сферической поверхности. При небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Шарик не возвращается в исходную точку.

3 опыт: безразличное равновесие: шарик неподвижно лежит на плоской поверхности. При небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю. Шарик после перемещения не меняет своё положение.

4.3. Применение принципов равновесия

Принципы устойчивого равновесия используются в строительстве зданий. Устойчивое равновесие корабля обеспечивает балласт в трюме.

Понятие устойчивости широко применяется в самолётостроении.

Устойчивость и управляемость летательного аппарата — взаимосвязанные свойства динамики полета.

Управляемость — свойство самолёта отвечать соответствующими линейными и угловыми перемещениями в пространстве на команды управления.

Устойчивость — свойство самолёта восстанавливать без вмешательства пилота кинематические параметры невозмущенного движения и возвращаться к исходному режиму полета после прекращения действия возмущений.

Устойчивое равновесие пассажирского самолёта обеспечивает верхнее расположение крыльев относительно фюзеляжа.

Неустойчивое равновесие применяется в строительстве военных самолётов.

Для достижения сверх манёвренности нужно снизить устойчивость самолёта до нулевой или даже отрицательной — ввести его в состояние неустойчивого равновесия. Например, обеспечить взаимное расположение вектора тяги ниже центра масс. И нужно увеличить тягу двигателей настолько, чтобы она превышала вес самолёта. В таком случае говорят, что удельная тяга больше единицы.

При этом управлять им вручную, когда органы управления связаны напрямую с рулями, становится невозможно. Управление берёт на себя автоматика, а лётчик, грубо говоря, только приказывает ей, что делать. Такой принцип применяется в системах управления истребителей 5-го поколения.

А все самолёты на земле находятся в состоянии безразличного равновесия.

Физику многие боятся, как огня, считая трудной. Однако понимание зависит от способа изложения. Поехали.

5.1. Описание системы падающего бутерброда

Распространено убеждение, что бутерброд практически всегда падает маслом вниз. Это связано с равновесием.

Лучший способ исследования в смысле объективности — поставить эксперимент. Нужно ронять на пол бутерброды до тех пор, пока вы не придете к определенному выводу. Но это негигиенично, неэкономично и неэтично. Верный результат можно получить и с помощью мысленного эксперимента. Правда, при условии, что вы умеете доводить мысленный эксперимент до конца.

Для упрощения представим себе, что бутерброд, стоит на ребре. Предположим, что стол резко убрали. Как поведёт себя бутерброд?

Принимаем, что в самом бутерброде при его падении не возникает никаких сил, которые давали бы предпочтение одной из двух ситуаций или они бесконечно малы: трение воздуха о масло и о хлеб одинаково, ветра нет.

Ну а теперь перейдём к расчётам.

5.2. Определение плотности хлеба и масла.

Для начала вычислим плотность масла и хлеба.

Источник