Что такое биекция в математике
Инъективная несюръективная функция (инъекция, а не биекция)
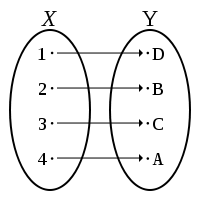
Инъективная сюръективная функция ( биекция )
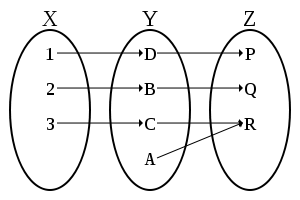
Неинъективная сюръективная функция (сюръекция, а не биекция)
Неинъективная несюръективная функция (также не биекция)
СОДЕРЖАНИЕ
Определение
Чтобы пара между X и Y (где Y не обязательно отличаться от X ) была биекцией, должны выполняться четыре свойства:
Примеры
Состав бейсбольной или крикетной команды
Места и студенты класса
В классе есть определенное количество мест. Группа студентов входит в комнату, и инструктор просит их сесть. Быстро осмотрев комнату, инструктор заявляет, что существует взаимное соответствие между набором студентов и набором сидений, где каждый студент сопоставляется с сиденьем, на котором они сидят. Что наблюдал преподаватель, чтобы прийти к такому выводу было это:
Инструктор смог сделать вывод, что мест было столько же, сколько и студентов, не считая ни одного набора.
Еще математические примеры и некоторые не-примеры
Перевернутые
В кратких математических обозначениях функция f : X → Y биективна тогда и только тогда, когда она удовлетворяет условию
для каждого y в Y существует единственный x в X с y = f ( x ).
Продолжая пример с расстановкой бейсбольных битов, определяемая функция принимает в качестве входных данных имя одного из игроков и выводит позицию этого игрока в порядке битья. Поскольку эта функция является биекцией, у нее есть обратная функция, которая принимает в качестве входных данных позицию в порядке отбивания и выводит игрока, который будет отбивать эту позицию.
Сочинение
Мощность
Характеристики
Теория категорий
Обобщение на частичные функции
Смотрите также
Примечания
использованная литература
Эта тема является базовой концепцией теории множеств и может быть найдена в любом тексте, который включает введение в теорию множеств. Почти все тексты, посвященные введению в написание доказательств, будут включать раздел по теории множеств, поэтому эту тему можно найти в любом из них:
Биективность
Функция 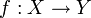
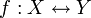
Биекцию также называют взаимно однозначным отображением. Множества, для которых существует биекция, называются равномощными.
Содержание
Примеры
Свойства
Использование модели
В информатике
Организация связи «один к одному» между таблицами реляционной БД на основе первичных ключей
См. также
Литература
Полезное
Смотреть что такое «Биективность» в других словарях:
Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия
ДЕФОРМАЦИЯ — 1) Д. аналитической структуры семейство аналитич. ространств (или связанных с ними аналитич. объектов), зависящее от параметров. Теория Д. возникла из задачи классификации всевозможных попарно не изоморфных комплексных структур на данном… … Математическая энциклопедия
Клеточный автомат — дискретная модель, изучаемая в математике, теории вычислимости, физике, теоретической биологии и микромеханике. Включает регулярную решётку ячеек, каждая из которых может находиться в одном из конечного множества состояний, таких как 1 и 0.… … Википедия
Функциональная зависимость — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
Область значений — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
Область определения — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
Образ (математика) — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
Отображение — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
Полный прообраз — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
Праобраз — Запрос «Отображение» перенаправляется сюда. Cм. также другие значения. В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое… … Википедия
Биекция
Инъективная несюръективная функция (инъекция, а не биекция)
Инъективная сюръективная функция (биекция)
Неинъективная несюръективная функция (также не биекция)
СОДЕРЖАНИЕ
Определение [ править ]
Чтобы пара между X и Y (где Y не должно отличаться от X ) было биекцией, должны выполняться четыре свойства:
Примеры [ править ]
Состав бейсбольной или крикетной команды, отбивающий мяч [ править ]
Сиденья и ученики в классе [ править ]
В классе есть определенное количество мест. Группа студентов входит в комнату, и инструктор просит их сесть. Быстро осмотрев комнату, инструктор заявляет, что существует взаимное соответствие между набором студентов и набором сидений, где каждый студент сопоставляется с сиденьем, на котором они сидят. Что наблюдал преподаватель, чтобы прийти к такому выводу было это:
Инструктор смог сделать вывод, что мест было столько же, сколько и студентов, не считая ни одного набора.
Дополнительные математические примеры и некоторые не-примеры [ править ]
Перевернутые [ править ]
В кратких математических обозначениях функция f : X → Y биективна тогда и только тогда, когда она удовлетворяет условию
для каждого y в Y существует единственный x в X с y = f ( x ).
Продолжая пример с расстановкой бейсбольных битов, определяемая функция принимает в качестве входных данных имя одного из игроков и выводит позицию этого игрока в порядке битья. Поскольку эта функция является биекцией, у нее есть обратная функция, которая принимает в качестве входных данных позицию в порядке отбивания и выводит игрока, который будет отбивать эту позицию.
Состав [ править ]
Мощность [ править ]
Свойства [ править ]
Теория категорий [ править ]
Обобщение на частичные функции [ править ]
Сравните с [ править ]
См. Также [ править ]
Заметки [ править ]
Ссылки [ править ]
Эта тема является базовой концепцией теории множеств и может быть найдена в любом тексте, который включает введение в теорию множеств. Почти все тексты, посвященные введению в написание доказательств, будут включать раздел по теории множеств, поэтому эту тему можно найти в любом из них:
только для инъекций
Инъективная функция не обязательно должна быть сюръективной (не все элементы кодомена могут быть связаны с аргументами), а сюръективная функция не обязательно должна быть инъективной (некоторые изображения могут быть связаны с более чем одним аргументом). Четыре возможных комбинации инъективных и сюръективных признаков показаны на соседних диаграммах.
СОДЕРЖАНИЕ
Инъекция
Ниже приведены некоторые факты, связанные с инъекциями:
Surjection
Ниже приведены некоторые факты, относящиеся к сюрпризам:
Биекция
Ниже приведены некоторые факты, относящиеся к предубеждениям:
Мощность
Примеры
Важно указать домен и кодомен каждой функции, поскольку при их изменении функции, которые кажутся одинаковыми, могут иметь разные свойства.
Характеристики
Теория категорий
История
Инъективно-сюръективно-биективная терминология (как существительные, так и прилагательные) была первоначально введена французской группой Бурбаки до их широкого распространения.
Биекция
Инъективная несюръективная функция (инъекция, а не биекция)
Инъективная сюръективная функция (биекция)
Неинъективная несюръективная функция (также не биекция)
СОДЕРЖАНИЕ
Определение [ править ]
Чтобы пара между X и Y (где Y не должно отличаться от X ) было биекцией, должны выполняться четыре свойства:
Примеры [ править ]
Состав бейсбольной или крикетной команды, отбивающий мяч [ править ]
Сиденья и ученики в классе [ править ]
В классе есть определенное количество мест. Группа студентов входит в комнату, и инструктор просит их сесть. Быстро осмотрев комнату, инструктор заявляет, что существует взаимное соответствие между набором студентов и набором сидений, где каждый студент сопоставляется с сиденьем, на котором они сидят. Что наблюдал преподаватель, чтобы прийти к такому выводу было это:
Инструктор смог сделать вывод, что мест было столько же, сколько и студентов, не считая ни одного набора.
Дополнительные математические примеры и некоторые не-примеры [ править ]
Перевернутые [ править ]
В кратких математических обозначениях функция f : X → Y биективна тогда и только тогда, когда она удовлетворяет условию
для каждого y в Y существует единственный x в X с y = f ( x ).
Продолжая пример с расстановкой бейсбольных битов, определяемая функция принимает в качестве входных данных имя одного из игроков и выводит позицию этого игрока в порядке битья. Поскольку эта функция является биекцией, у нее есть обратная функция, которая принимает в качестве входных данных позицию в порядке отбивания и выводит игрока, который будет отбивать эту позицию.
Состав [ править ]
Мощность [ править ]
Свойства [ править ]
Теория категорий [ править ]
Обобщение на частичные функции [ править ]
Сравните с [ править ]
См. Также [ править ]
Заметки [ править ]
Ссылки [ править ]
Эта тема является базовой концепцией теории множеств и может быть найдена в любом тексте, который включает введение в теорию множеств. Почти все тексты, посвященные введению в написание доказательств, будут включать раздел по теории множеств, поэтому эту тему можно найти в любом из них: