Что такое бинарная система
Двоичная система счисления
Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.
Немного истории
Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.
Таблица и алфавит
Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.
1001102 = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 3810
Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:
| Делимое | 38 | 19 | 9 | 4 | 2 |
|---|---|---|---|---|---|
| Делитель | 2 | 2 | 2 | 2 | 2 |
| Частное | 19 | 9 | 4 | 2 | 1 |
| Остаток | 0 | 1 | 1 | 0 | 0 |
Для перевода в другие системы необходимо:
Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:
| Двоичная | Восьмеричная | Шестнадцатеричная |
|---|---|---|
| 0 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | |
| 1001 | 9 | |
| 1010 | A | |
| 1011 | B | |
| 1100 | C | |
| 1101 | D | |
| 1110 | E | |
| 1111 | F |
110010012 = 11 001 001 = 011 001 001 = 3118
110010012 = 1100 1001 = С916
Представление двоичных чисел
В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.
Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.
Прямой код предполагает приписывание единицы в начале без изменений записи:
| A > 0 | Aпр = 0A | 1010112; Aпр = 01010112 |
| A ≤ 0 | Aпр = 1|A| | -1010112; Aпр = 11010112 |
Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:
| A > 0 | Aобр = 0A | 1010112; Aобр = 01010112 |
| A ≤ 0 | Aобр = 1 A | -1010112; Aобр = 10101002 |
Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:
| A > 0 | Aдоп = 0A | 1010112; Aдоп = 01010112 |
| A ≤ 0 | Aдоп = 1 A + 1 | -1010112; Aдоп = 10101012 |
Применение двоичной системы в информатике
Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.
Двоичная система счисления
Все что-то слышали о двоичной системе счисления, все знают, что это некий «язык компьютеров». Но почему именно так? Почему не пользоваться привычной десятичной системой? В чем, собственно, смысл?
Что такое двоичная система? Это позиционная система счисления с основанием 2. Вот только цифры «два» в ней нет, есть только 0 и 1, и так как цифры две, система называется двоичной (бинарной).
Современный цифровой язык, это ноли и единицы, больше ничего и не нужно. Самое интересное, так называемый машинный код использовался людьми задолго до появления самих машин, а, возможно, даже по появления чисел.
Зачем нужна двоичная система
Двоичная, или бинарная система счисления удобна своей простотой. С помощью комбинации нолей и единиц можно записать любой число и любую букву, что угодно может быть закодировано таким образом.
Но главное, что значения всего два. Это либо «ноль», либо «единица». Сигнал либо есть, либо его нет, свет горит или не горит, есть отверстие или нет (перфокарта), намагничен сектор или размагничен… Аналогии можно приводить бесконечно. Главное, что кодировать сигнал просто. Не нужно создавать сложные механизмы или устройства, достаточно только двух состояний.
Например, еще до того как люди научились считать и писать, сигналы передавались с помощью дыма от костра или ударов в барабаны.
Бинарная система — это просто, ничего проще просто нет. Есть, конечно, и древнейшая унитарная система, где значение всего одно (например, только 1) но с ее помощью нельзя ничего закодировать.
В любой микросхеме транзистор может прибывать в двух положениях «закрыто» или «открыто» (0 или 1) ток пропускается или нет.
Кстати, азбука Морзе — это тоже двоичный код (точка или тире), так же, как и древнейшая сигнальная система — «оптический телеграф». Это это просто огонь костра, который можно закрыть и открыть (огонь есть, или огня нет) ночью, а днем так же использовать дым.
Да, двоичная система используется потому, что с ее помощью удобно кодировать информацию, нужны всего 2 значения. Но удобно ли это считать?
Как считать
Как использовать двоичную систему для записи чисел? Так же как и десятичную. Самым простым примером можно считать кодовый замок, такой как на чемоданах. Каждый диск которого, вращается и может принимать значение от 0 до 9. Достаточно представить, что вместо десяти цифр есть только 2, ноль и единица.
Так как система позиционная, это будет выглядит так:
Сейчас здесь записано число «ноль». Чтобы получилась единица, нужно провернуть крайний правый диск один раз.
Начинается самое интересное, как будет выглядеть число «два»? Крутим правое колесико… И снова получаем 0, ведь других значений нет. Нужно поступить так же, как и в десятичной системе, перенести разряд влево. Только в десятичной, это происходит когда значение превышает 9, а в двоичной сразу после 1.
| Двоичная система | Десятичная система |
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
Сто в двоичной системе — это 1100100.
Очень интересно в бинарной системе выглядит таблица умножения:
Легко запомнить, неправда ли? 0*0=0, 0*1=0, 1*1=1… И все!
Все математические операции выполняются точно так же
Если сложит в столбик то получается нагляднее
100
Складываем ноли, получаем 0, складываем две единицы, получаем ноль (2 раза провернули диск) и единичку переносим вправо.
Как видите, математика та же, вот только запись чисел неудобная, слишком много нолей и единиц, для человека — неудобно, машине же все равно.
Так же как с цифрами можно поступить с буквами. Латинская буква «a» будет выглядеть как 01001010 кириллическая «а» — 000011100010111000011001, и даже пробел — 00010100.
История создания
Ясно, что человечество пользовалось двоичным кодом очень давно. И сигнальные системы с дымом от костров и даже китайская Книга Перемен (700 лет до нашей эры) с ее гексаграммами известны очень давно. Но окончательно практический смысл бинарный код получил совсем недавно (если не считать азбуку Морзе).
Великий Лейбниц занимался двоичной системой в 17 веке, но применить бинарную систему счисления было особо негде. В том же Веке Паскаль создал свою счетную машину (суммирующую), использующую десятичную систему. Оказалось, что считать на таком «калькуляторе» не так уж и удобно.
Суммирующая машина Паскаля (десятичная)
И только в 40-х годах 20 веке, вместе с появлением первых электронный вычислительных машин двоичный код явил всю свою безусловную полезность и красоту. Именно как машинный язык. Записывать информацию в котором гораздо проще, чем привычными нам средствами, буквами и цифрами.
То же самое, в двоичном коде можно сделать проще
Для чего нужна двоичная система счисления сегодня, мы прекрасно знаем, у каждого в кармане есть смартфон. На самом деле, ноли и единицы используются намного чаще, чем десятичная система, даже если мы, люди, этого и не видим. Не удивительно, мы использовали двоичную систему на протяжении всей истории, но до эры машин даже не замечали этого.
Двоичная система
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
Содержание
Таблица умножения двоичных чисел
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7 15 / 16″, 3 11 / 32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо 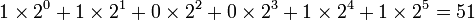
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)» [1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
Полезное
Смотреть что такое «Двоичная система» в других словарях:
ДВОИЧНАЯ СИСТЕМА — ДВОИЧНАЯ СИСТЕМА, в математике система счисления, имеющая ОСНОВАНИЕ 2 (десятичная система имеет основание 10). Она наиболее пригодна для работы с компьютерами, поскольку отличается простотой и соответствует двум положениям (открытое 0 и закрытое… … Научно-технический энциклопедический словарь
двоичная система — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN binary system … Справочник технического переводчика
двоичная система — dvejetainė sistema statusas T sritis automatika atitikmenys: angl. binary system vok. Binärsystem, n rus. двоичная система, f pranc. système binaire, m … Automatikos terminų žodynas
двоичная система — dvejetainė sistema statusas T sritis fizika atitikmenys: angl. binary system; dyadic system vok. Binärsystem, n; Dualsystem, n rus. двоичная система, f pranc. système binaire, m … Fizikos terminų žodynas
Двоичная система — Жарг. студ. Шутл. Сильное опьянение. ПБС, 2002 … Большой словарь русских поговорок
Двоичная система счисления — позиционная система счисления с основанием 2, в которой для записи чисел используются цифры 0 и 1. См. также: Позиционные системы счисления Финансовый словарь Финам … Финансовый словарь
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — ДВОИЧНАЯ система СЧИСЛЕНИЯ, способ записи чисел, при котором используются две цифры 0 и 1. Две единицы 1 го разряда (т.е. места, занимаемого в числе) образуют единицу 2 го разряда, две единицы 2 го разряда образуют единицу 3 го разряда и т.д.… … Современная энциклопедия
Двоичная система счисления — ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ, способ записи чисел, при котором используются две цифры 0 и 1. Две единицы 1 го разряда (т.е. места, занимаемого в числе) образуют единицу 2 го разряда, две единицы 2 го разряда образуют единицу 3 го разряда и т.д.… … Иллюстрированный энциклопедический словарь
Двоичная система исчисления — система, использующая для представления буквенно цифровых и иных символов наборы комбинаций цифр 1 и 0, основа используемых в цифровых ЭВМ кодов … Издательский словарь-справочник
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — позиционная система счисления с основанием 2, в которой имеются две цифры 0 и 1, и их последовательностями записываются все натуральные числа. Напр. цифра 2 записывается как 10, цифра 4 = 22 как 100, число 900 как 11 значное число: 11 110 101 000 … Большая политехническая энциклопедия
Что такое бинарный код и как он работает?
Бинарная система представляет собой систему представления чисел с использованием шаблона единиц и нулей. Впервые изобретенная Готфридом Лейбницем в 17 веке, система двоичных чисел стала широко использоваться, когда компьютерам требовался способ представления чисел с помощью механических переключателей.
Что такое двоичный код?
Цифровой или ноль — это просто электрический сигнал, который либо включается, либо выключается внутри аппаратного устройства, такого как ЦП, которое может хранить и вычислять многие миллионы двоичных чисел.
Двоичные числа состоят из серии из восьми «битов», которые известны как «байт». Бит представляет собой единицу или ноль, составляющий 8-битное двоичное число. Используя коды ASCII, двоичные числа также могут быть преобразованы в текстовые символы для хранения информации в памяти компьютера.
Как работают двоичные числа
Преобразование двоичного числа в десятичное число очень просто, если учесть, что компьютеры используют двоичную систему с основанием 2. Размещение каждой двоичной цифры определяет ее десятичное значение. Для 8-разрядного двоичного числа значения рассчитываются следующим образом:
Сложив вместе отдельные значения, где бит имеет единицу, вы можете представить любое десятичное число от 0 до 255. Гораздо большее число может быть представлено путем добавления большего количества битов в систему.
Когда компьютеры имели 16-разрядные операционные системы, наибольшее число, которое ЦП мог вычислить, составляло 65 535. 32-разрядные операционные системы могут работать с отдельными десятичными числами размером до 2 147 483 647. Современные компьютерные системы с 64-разрядной архитектурой способны работать с впечатляюще большими десятичными числами — до 9 223 372 036 854 775 807!
Представление информации с ASCII
Теперь, когда вы понимаете, как компьютер может использовать двоичную систему счисления для работы с десятичными числами, вы можете задаться вопросом, как компьютеры используют ее для хранения текстовой информации.
Как объяснять двоичную систему счисления
Кто-то только входит в IT-мир, кто-то объясняет информатику своему чаду.
Довольно быстро вы обнаружите, что не так-то просто объяснить, как работает двоичный счёт.
Это вам очевидно, что после 11 идёт 100, а новичку это ещё долго может быть непонятно.
Так вот, чтобы увеличить скорость понимания, мы решили сделать дидактический материал.
Проблема
Важно отметить, что даже распиаренный курс Гарвардского университета по компьютерным наукам «CS50» не помогает.
Парень из американского университета просто заявляет, что «нуль — это нуль», «один — это один», а потом идёт 10, а потом 11. Понятно? Думаю, нет. Вот спросите кого-то, кто не программист, а каким будет следующее число — высока вероятность, что он не сможет ответить. Слишком быстро проскочили идею о переносе разряда.
То же самое касается школьных методов перевода: во-первых, методы эти академически сухи, во-вторых, не интуитивны — например, не очевидно, почему после каскадного деления на 2 нужно ставить биты задом наперёд.
А если непонятно, то и не интересно. А если нет интереса, то и запоминается с трудом.
Мы это всё учли, и решили сделать интересное и постепенное объяснение.
Что мы предлагаем
Сначала нужно объяснить, как вообще работает обычная десятичная система счисления — и про конечный «алфавит» цифр, и про идею переноса разряда. Так развивается понимание принципа «системы счисления».
Только потом можно переходить к идее двоичной системы — и вот обучаемый уже медленно, но довольно уверенно говорит «1, 10, 11, 100».
Далее, мы решили попробовать совсем не школьный метод — объяснение двоичного счёта на пальцах: это когда загнутый палец это 0, а разогнутый это 1.
Я проверял это на подростках: показываешь им: «это 1, это 2, это 3 — теперь покажите мне 4». И весь класс сосредоточенно, медленно показывает средние пальцы. Отличницы в эсхатологическом восторге, задние парты тыкают друг другу в лицо и кричат «на тебе четвёрку!».
Провокативно? Да. Запоминается? 100%.
Теперь, когда тема стала «своей», можно переходить к теме перевода чисел из одной системы счисления в другую — начать лучше с классического школьного сухого перевода (если честно, то больше чтобы постращать).
А уже потом с помощью анимации объяснить идею перевода прямо на пальцах, и потом опять же на пальцах пересчитать число 132 в средние пальцы уже на обеих руках.
На десерт показываем, где двоичная и 16-ричная системы применяется в реальной жизни.
Двоичная система — это например QR-коды вокруг нас.
А 16-ричная система это в основном коды цветов в CSS и хеши разных стилей, от MD5 до UUID.
Итак, вот весь пакет видео-уроков (они бесплатные, в Ютубе):





