Что такое булева логика
Булева логика
Основоположником её является Дж. Буль, английский математик и логик, положивший в основу своего логического учения аналогию между алгеброй и логикой. Алгебра логики стала первой системой математической логики, в которой алгебраическая символика стала применяться к логическим выводам в операциях с понятиями, рассматриваемыми со стороны их объёмов. Буль ставил перед собой задачу решить логические задачи с помощью методов, применяемых в алгебре. Любое суждение он пытался выразить в виде уравнений с символами, в которых действуют логические законы, подобные законам алгебры.
Впоследствии усовершенствованием алгебры логики занимались У. С. Джевонс, Э. Шрёдер, П. С. Порецкий, Ч. Пирс, Г. Фреге, разработавший теорию исчисления высказываний, Д. Гильберт, добившийся успехов в области применения метода формализации в операциях с логическими высказываниями. Внесли свой вклад Б. Рассел, придавший вместе с А. Уайтхедом, математической логике современный вид; И. И. Жегалкин, заслугой которого явилась дальнейшая разработка исчисления классов и значительное упрощение теории операций логического сложения; В. И. Гливенко вынес предмет алгебры логики далеко за рамки изучения объёмных операций с понятиями.
Алгебра логики в её современном изложении занимается исследованием операций с высказываниями, то есть с предложениями, которые характеризуются только одним качеством — истинностным значением (истина, ложь). В классической алгебре логики высказывание одновременно может иметь только одно из двух истинностных значений: «истина» или «ложь». Алгебра логики исследует также высказывания — функции, которые могут принимать значения «истина» и «ложь» в зависимости от того, какое значение будет придано переменной, входящей в высказывание — функцию.
Содержание
Определение
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.
а логический ноль 0 и логическая единица 1 — константы.
Также используются названия:
Аксиомы
Логические операции
Простейший и наиболее широко применяемый пример такой алгебраической системы строится с использованием множества B, состоящего всего из двух элементов:
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено»), комплексную логику и др.
Свойства логических операций
История
Своим существованием наука «алгебра логики» обязана английскому математику Джорджу Булю, который исследовал логику высказываний. Первый в России курс по алгебре логики был прочитан П. С. Порецким в Казанском государственном университете.
Булевы операции
Битовые операции, иногда также булевы или логические операции [1] — операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике.
Содержание
Введение
Булевы операции и математическая логика
Булевы операции очень близки (хотя и не тождественны) логическим связкам в классической логике. Бит можно рассматривать как логическое суждение — его значениями являются 1 «истина» и 0 «ложь». При такой интерпретации известные в логике связки конъюнкции, дизъюнкции, импликации, отрицания и другие имеют представление на языке битов. И наоборот, битовые операции легко описываются на языке исчисления высказываний.
Однако, связкам математической логики более соответствуют логические операции в т.ч. в программировании, нежели собственно битовые операции.
Булевы операции как основа цифровой техники
Булевы операции лежат в основе обработки цифровых сигналов. А именно, посредством них мы можем из одного или нескольких сигналов на входе получить новый сигнал, который в свою очередь может быть подан на вход одной или нескольким таким операциям. По сути, именно булевы операции в сочетании с запоминающими элементами (напр. триггерами) реализуют всё богатство возможностей современной цифровой техники.
Список битовых операций
«(Логическое) И» (and) — аналог конъюнкции в логике. Иногда называется логическим умножением.
В булевой логике:  | В языке C: & |
Выдаёт 1 если оба входа равны 1, в противном случае 0. Если один из аргументов равен 1, то результат «И» равен другому. Если один из аргументов равен 0, то результат «И» равен 0 независимо от значения другого аргумента.
«(Логическое) НЕ» (not), инвертирование — аналог отрицания в логике.
В булевой логике:  | В языке C: Данная унарная операция (с одним входом) заменяет 0 на 1 и наоборот. Реализующий её элемент называется инвертором. «(Логическое) ИЛИ» (or) — аналог дизъюнкции в логике.
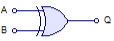
Выдаёт 1 если и только если хотя бы один из входов равен 1. Операция, двойственная AND: при инвертировании выхода и всех входов (т.е. при замене 0 и 1 местами) «И» и «ИЛИ» взаимно превращается друг в друга. Исключающее ИЛИ«Исключающее ИЛИ» (xor), «сложение по модулю 2» — аналог исключающего ИЛИ в логике.
Если один из аргументов равен 0, то результат равен другому. Если один из аргументов равен 1, то результат равен отрицанию другого аргумента. Первое русское название операции обусловлено тем, что результат данной операции отличается от результата «ИЛИ» только в одном случае из 4 случаев входа — обоих 1 (случай одновременной истинности аргументов «исключается»). Ещё в русской грамматике значение данной логической связки передаётся союзом «либо». Второе название — тем, что действительно является сложением в кольце вычетов по модулю 2, из чего следуют некоторые интересные свойства. Например, в отличие от вышеописанных «И» и «ИЛИ» данная операция является обратимой, или инволютивной: В графике «исключающее ИЛИ» применяется при выводе спрайтов на картинку — повторное её применение убирает спрайт с картинки. Благодаря инволютивности же эта операция нашла применение в криптографии как простейшая реализация идеального шифра (шифра Вернама). «Исключающее ИЛИ» также может использоваться для обмена двух переменных, используя алгоритм обмена при помощи исключающего ИЛИ. Операции от многих аргументовОперации «И», «ИЛИ» и «исключающее ИЛИ» являются не только коммутативными, но и ассоциативными, и потому легко обобщаются на случай нескольких аргументов (входов). Прочие бинарные операции
Стрелка Пирса является результатом инвертирования результата «ИЛИ» своих аргументов, выдаёт значение 1 только когда оба входа 0. «И-НЕ» (nand), или «штрих Шеффера».
Двойственная стрелке Пирса операция: является результатом инвертирования результата «И» своих аргументов, выдаёт значение 0 только когда оба входа 1. Известна простотой реализации в ТТЛ. Импликация («если-то») — аналог импликации в логике.
Совпадает с «ИЛИ» с инвертированным первым аргументом, выдаёт значение 0 только когда первый вход 1 а второй — 0. Данная операция не является коммутативной, в отличие от всех вышеописанных бинарных операций. Её можно понимать как арифметическое Эквиваленция. Выдаёт 1 если и только если оба аргумента равны между собой. Является результатом инвертирования результата «исключающего ИЛИ» своих аргументов. Она же и двойственна исключающему «ИЛИ» в вышеописанном смысле. Сводная таблица истинности булевых операций
x) | (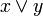 ) ) (x|y) | (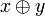 ) ) (x^y) | 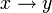 ( (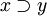 ) ) (( x)|y) | 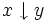 (( y)) | 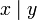 ( (x&y)) | ||||||||||||||||||||
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | ||||||||||||||||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | ||||||||||||||||||
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | ||||||||||||||||||
Операции над битовыми векторами
Обобщение операций на булеву алгебру
Тем не менее, ничто не мешает рассматривать эти регистры именно как битовые векторы и проводить булевые операции покомпонентно (бит номер k значения есть результат операция от битов номер k аргументов). Кстати, математически говоря, булевы операции распространяются таким образом на произвольную булеву алгебру. Таким образом мы получаем операции побитового И, ИЛИ, НЕ, искл. ИЛИ и т. д. Как арифметические, данные операции не обладают хорошими свойствами за исключением побитового НЕ, которое для чисел в дополнительном коде совпадает с вычитанием из −1 (
Битовые сдвиги
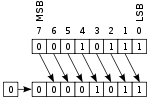
К битовым операциям также относят битовые сдвиги. При сдвиге значения битов копируются в соседние по направлению сдвига. Различают несколько видов сдвигов — логический, арифметический и циклический, в зависимости от обработки крайних битов.
Также различают сдвиг влево (в направлении от младшего бита к старшему) и вправо (в направлении от старшего бита к младшему).
Логический сдвиг
При логическом сдвиге значение последнего бита по направлению сдвига теряется (копируясь в бит переноса), а первый приобретает нулевое значение.
Логические сдвиги влево и вправо используются для быстрого умножения и деления на 2, соответственно.
Арифметический сдвиг
Арифметический сдвиг аналогичен логическому, но значение слова считается знаковым числом представленному дополнительным кодом. Так при правом сдвиге старший бит сохраняет свое значение. Левый арифметический сдвиг идентичен логическому.
Циклический сдвиг
При циклическом сдвиге, значение последнего бита по направлению сдвига копируется в первый бит (и копируется в бит переноса).
Также различают циклический сдвиг через бит переноса — при нем первый бит по направлению сдвига получает значение из бита переноса, а значение последнего бита сдвигается в бит переноса.
2-адическая интерпретация
Практические применения
Физическая реализация битовых операций
Реализация битовых операций может в принципе быть любой: механической, электромеханической, гидравлической, пневматической, оптической и даже химической.
В первой половине XX века вместо транзисторов применяли электромеханические реле и электронные лампы.
В пожароопасных и взрывоопасных условиях до сих пор применяют пневматические логические устройства (пневмоника).
В квантовых вычислениях из перечисленных булевых операций реализуются только НЕ и искл. ИЛИ (с некоторыми оговорками). Квантовых аналогов И, ИЛИ и т.д. не существует.
Схемы аппаратной логики
Результат операции ИЛИ-НЕ или ИЛИ ото всех битов двоичного регистра проверяет, равно ли значение регистра нулю; то же самое взятое от выхода искл. ИЛИ двух регистров проверяет равенство их значений между собой.
Битовые операции применяются в знакогенераторах и графических адаптерах; особенно велика была их роль в адаптере графический ускоритель.
Использование в программировании
Благодаря реализации в арифметическом логическом устройстве (АЛУ) процессора многие их регистровые битовые операции аппаратно доступны в языках низкого уровня. В большинстве процессоров реализованы в качестве инструкции регистровый НЕ; регистровые двухаргументные И, ИЛИ, исключающее ИЛИ; проверка равенства нулю (см. выше); три типа битовых сдвигов, а также циклические битовые сдвиги.
Регистровая операция И используется для сброса конкретных битов по битовой маске, ИЛИ — для установки, исключающее ИЛИ — для инвертирования битов регистра по маске.
Так, например, в сетевых интернет-технологиях операция И между значением IP-адреса и значением маски подсети используется для определения принадлежности данного адреса к подсети.
См. также
Примечания
Полезное
Смотреть что такое «Булевы операции» в других словарях:
Битовые операции — Не следует путать с булевой функцией. Битовая операция в программировании некоторые операции над цепочками битов. В программировании, как правило, рассматриваются лишь некоторые виды этих операций: логические побитовые операции и… … Википедия
ЛОГИЧЕСКИЕ ОПЕРАЦИИ — логич. операторы, логич. связки, функции, преобразующие выражения логич. исчислений (формальных логич. систем); подразделяются на пропозициональные (сен тенциональные) связки, с помощью которых образуются выражения логики высказываний, и… … Философская энциклопедия
Битовая операция — Битовые операции, иногда также булевы или логические операции[1] операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике. Содержание 1 Введение 1.1 … Википедия
Инвертор (логический элемент) — Битовые операции, иногда также булевы или логические операции[1] операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике. Содержание 1 Введение 1.1 … Википедия
Булева алгебра — Эта статья об алгебраической системе. О разделе математической логики, изучающем высказывания и операции над ними, см. Алгебра логики. Булевой алгеброй[1][2][3] называется непустое множество A с двумя бинарными операциями (аналог конъюнкции),… … Википедия
IARP — International Aging Research Portfolio URL … Википедия
БУЛЕВА АЛГЕБРА — булева решетк а, частично упорядоченное множество специального вида. Б. а. наз. дистрибутивная решетка (дистрибутивная структура), имеющая наибольший элемент 1 единицу Б. а., наименьший элемент 0 нуль Б. а. и содержащая вместе с каждым своим… … Математическая энциклопедия
Матрица достижимости — простого ориентированого графа бинарная матрица замыкания по транзитивности отношения (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.… … Википедия
Векторная графика — Пример, показывающий разницу между векторной, фрактальной и растровой графикой при увеличении. a: исходное векторное изображение; b: иллюстрация, увеличенная в 8 раз как векторное изображение; c: иллюст … Википедия
Глава 11. Булева логика: критерии И, ИЛИ
Это глава из книги: Майкл Гирвин. Ctrl+Shift+Enter. Освоение формул массива в Excel.
В предыдущих главах вы уже использовали И критерий при написании формул. Например:
Рис. 10.24 – суммирование с использованием двух критериев
=СУММЕСЛИМН(C8:C19;A8:A19; » >= » &A2;A8:A19; » » &B2;B8:B19;C2)
Рис. 10.25 – также суммирование с использованием двух критериев =БДСУММ(A7:C19;C7;A1:C2)
Рис. 4.39 – нахождение минимума на основе двух критериев
=АГРЕГАТ(15;6;$C$3:$C$13/(($A$3:$A$13<>$F$2)*($B$3:$B$13=E5));1)
Во всех четырех формулах И критерий означает, что все условия, или логические тесты должны быть удовлетворены для включения данных в расчет. В этой главе мы подробно рассмотрим также ИЛИ критерий.
Булеву алгебру предложил в 1854 году Джордж Буль. Логическими (булевыми) называют тип данных, которые имеет только два варианта значений: ИСТИНА и ЛОЖЬ (или 1 и 0).
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Я употребляю термины И критерий, ИЛИ критерий, потому что в Excel они часто используются для создания отчетов, выборки данных или расчетов, основанных на наборе критериев. Кроме того, я обычно использую синоним булева математика вместо булевой логики, потому что использую умножение для И критерия, и суммирование – для ИЛИ критерия.
Примечание: вот некоторые синонимичные термины, которые вы можете встретить в литературе:
Ниже приведены все возможные комбинации из двух и трех логических значений в варианте И критерия и ИЛИ критерия:
Для И критерия используется умножение, так что если хоть один элемент равен 0 (ЛОЖЬ), конечный результат будет 0 (ЛОЖЬ). И критерий вернет значение 1 (ИСТИНА) в единственном случае – когда все элементы равны 1.
Для ИЛИ критерия используется сложение, так того если хоть один элемент равен 1 (ИСТИНА), конечный результат будет 1 (ИСТИНА). ИЛИ критерий вернет значение 0 (ЛОЖЬ) в единственном случае – когда все элементы равны 0.
Ключевая концепция, которая используется при построении больших формул, заключается в том, что критерии И, ИЛИ являются фильтрами для отбора «нужных» данных. Давайте рассмотрим некоторые примеры.
И критерий (рис. 11.1–11.7). Во всех примерах используется 4 критерия. Это означает, что все четыре проверки должны вернуть значение ИСТИНА для того чтобы элемент данных был включен в расчет.
Рис. 11.1. Формулы [1]–[4] используют И критерии; [5] – логическое умножение; [6] – логическое умножение и деление; [7] – функцию ЕСЛИ и И критерий.
Примечания: подробнее о формулах [1], [2], [3] и [5] см. главу 10, [4], [6] и [7] – главу 4.
Рис. 11.2. Сводная таблица с помощью фильтров суммирует на основе И критерия
Рис. 11.3. Опция Таблица с соответствующими фильтрами и строкой Итоги позволяет вычислить среднее (используются И критерий); подробнее о Таблицах см. главу 7
Рис. 11.4. Опция Фильтр позволяет фильтровать данные, используя И критерий; выделите ячейки А1:D1, перейдите на закладку Данные в область Сортировка и фильтр и нажмите кнопку Фильтр; с помощью кнопок в правой части каждого столбца выберите требуемые значения
Рис. 11.5. Расширенный фильтр может сделать выборку на основе И критерия; создайте область критериев, перейдите на закладку Данные в область Сортировка и фильтр и нажмите кнопку Дополнительно; в открывшемся окне Расширенный фильтр заполните поля и нажмите Ok
Рис. 11.6. Функция И с четырьмя логическими проверками в дополнительном столбце. Можно обойтись и без дополнительного столбца, если использовать вместо СЧЁТЕСЛИ функцию СЧЁТЕСЛИМН; подробнее см. главу 15
Рис. 11.7. Вместо того, чтобы, использовать функцию И, вы можете перемножить операторы сравнения, и получить во вспомогательном столбце единицы и нули
Чтобы лучше понять, как работает И критерий, давайте подробнее изучим пару формул, с рис. 11.1.
ИЛИ критерий. При запуске логического теста ИЛИ достаточно чтобы хотя бы одна проверка вернула значение ИСТИНА, чтобы весть тест вернул значение ИСТИНА. Только в том случае, когда все условия вернули значение ЛОЖЬ, тест вернет ЛОЖЬ. Характерные фразы при описании критерия ИЛИ: «по крайней мере один», «один или более».
Далее показаны два примера, которые иллюстрируют работу логического критерия ИЛИ. На рис. 11.8 показан список менеджеров (столбец А) и значение формулы с критерием ИЛИ (столбец B). Логическое ИЛИ выясняет: «Имя менеджера Gidget или Rodger?». Обратите внимание, что, поскольку использовано два отдельных вопроса к одной ячейке, вы не можете получить в столбце В два значения ИСТИНА. Все ответы сводятся к нулям и единицам.
Рис. 11.8. Ответ на вопрос «Gidget или Rodger?» не может вернуть два значения ИСТИНА; критерий ИЛИ, применяемый к одной ячейке решает проблему
Рис. 11.9. Кредит может быть выдан, если чистые активы > 100 000 или рейтинг >= 3,5
Почему важно различать вопросы ИЛИ, которые могут давать более одного значения ИСТИННА, и вопросы ИЛИ, которые возвращают не более одного значения ИСТИННА? Это важно для построения формул. Вы должны быть особенно осторожны с вопросами ИЛИ, которые могут возвращать несколько значений ИСТИННА. Я бы сказал, что есть два типа формул с логическим ИЛИ.
Логический тест ИЛИ, который не может вернуть более одного значения ИСТИНА:
Логический тест ИЛИ, который может вернуть более одного значения ИСТИНА:
Чтобы глубже понять две указанные разновидности тестов, сравните формулы в следующих двух примерах. На рис. 11.10 показан набор формул, в которых критерий ИЛИ, не можете вернуть более одного значения ИСТИНА.
Рис. 11.10. Примеры формул на основе критерия ИЛИ, возвращающего не более одного значения ИСТИНА
Формула [1]. Поскольку обе функции СЧЁТЕСЛИ извлекают данные из одного и того же столбца (А), а в одной ячейке не может одновременно быть и Gidget и Rodger, критерий ИЛИ для каждой ячейки из диапазоне А2:А6 вернет, либо 0, либо 1.
Формула [2]. Вы используете БСЧЁТА (а не БСЧЁТ), потому что вы подсчитываете вхождение текста, а не чисел. Критерии ИЛИ для функции базы данных должны быть введены в соседних строках в одном или разных столбцах (в отличие от критериев И, которые должны быть в одной строке в соседних столбцах). Если вам нужно подсчитать количество ячеек с текстовыми строками нулевой длины, БСЧЁТА справится и с этим.
Формула [3]. (A2:A6=C2)+(A2:A6=C3) → <ИСТИНА:ЛОЖЬ:ЛОЖЬ:ЛОЖЬ:ЛОЖЬ>+ <ЛОЖЬ:ИСТИНА: ЛОЖЬ:ИСТИНА:ЛОЖЬ>→ <1:1:0:1:0>. Нет необходимости в двойном отрицании, потому что вы уже использовали математический оператор сложения, преобразующий логические значения в числа.
Формула [4]. <=СУММ(ЕСЛИ((A2:A6=C2)+(A2:A6=C3);1))>→ <=СУММ(ЕСЛИ(<1:1:0:1:0>;1))> → <=СУММ(<1:1:ЛОЖЬ:1:ЛОЖЬ>)>. Аргумент лог_выражение функции ЕСЛИ содержит массив чисел. Это работает, потому что лог_выражение интерпретирует любое ненулевое значение, как ИСТИННА, и ноль как ЛОЖЬ.
Эти пять формулы удивительные! Но чтобы в полной мере сравнивать их, давайте посмотрим, как они справляются с большим набором данных. На рис. 11.11 приведено 500 строк и 6 критериев.
Рис. 11.11. Формулы аналогичные рис. 11.10, но для 500 строк и 6 критериев
Видно, что формулы [1], [3] и [4] значительно усложнились, в то время, как формулы [2] и [5] остались короткими. С точки зрения набора, формулы [2] и [5] предпочтительнее. В тоже время, самой быстрой является формула [1]. Немного уступают ей в скорости работы формулы [2] и [5], а самые медленные [3] и [4].
Рис. 11.13. Каждый логический тест ИЛИ обращается у двум различным ячейкам и, следовательно, может вернуть два значения ИСТИНА; формулы масиива обращаются к двум столбцам (В и С)
Формула [1]. <=СУММ(ЕСЛИ((B2:B6>E3)+(C2:C6>=E5);1))> → <=СУММ(ЕСЛИ(<1:2:0:1:0>;1))> → <=СУММ(<1:1:ЛОЖЬ:1:ЛОЖЬ>)>. Красота этой формулы заключается в том, что вы можете разместить проверку на основе логического ИЛИ в аргументе лог_выражение функции ЕСЛИ. В свою очередь, аргумент лог_выражение интерпретирует любое ненулевое число, как ИСТИННА, а ноль, как ЛОЖЬ. Т.е., для аргумента лог_выражение <1:2:0:1:0>= (<ИСТИННА:ИСТИННА:ЛОЖЬ: ИСТИННА:ЛОЖЬ>. Далее функция ЕСЛИ заменяет ИСТИНА на 1, а ЛОЖЬ оставляет без изменения (аргумент значение_если_ложь опущен). Обратите внимание, что в формуле [1] вдвое меньше операций с массивами, чем в формуле [3], что позволяет формуле [1] быстрее выполнять рассчеты.
Формула [2]. Поскольку используются критерии ИЛИ, вы должны разместить область критериев в разных столбцах (G3 и H4).
Рассмотренные концепции могут быть применены также для функций суммирования, нахождения среднего, минимума и максимума (рис. 11.15–11.17).
Рис. 11.15. Расчет суммы и среднего значения на основе критерия ИЛИ, применяемого к одному столбцу; логическая проверка в каждой ячейке не может вернуть более одного значения ИСТИНА
Рис. 11.16. Расчет суммы и среднего значения на основе критерия ИЛИ, применяемого к двум столбцам; логическая проверка в каждой ячейке может вернуть более одного значения ИСТИНА; формула [4] дает неверные ответ из-за двойного счета по ряду 4 (лишние 77 970)
Рис. 11.17. Расчет МИН и МАКС с использованием критерия ИЛИ, применяемого к двум столбцам; логическая проверка в каждой ячейке может вернуть более одного значения ИСТИНА; обратите внимание, что в формуле [2] у функции АГРЕГАТ первый параметр (15) соответствует функции НАИМЕНШИЙ; при этом внутри формулы используется деление, чтобы отфильтровать (не включать в расчет) нулевые значения; в формуле [4] первый параметр (14) соответствует функции НАИБОЛЬШИЙ; здесь используется обычное умножение, так как нули не повлияют на результат (при этом и деление подошло бы); формулы [1] и [3] с функцией ЕСЛИ содержат на один оператор массива больше, чем формулы [2] и [4].
Одновременное использование критериев И, ИЛИ в одной формуле. Когда у вас есть логический тест, который сочетает в себе критерии И, ИЛИ, вы действуете в зависимости от того, может ли критерий ИЛИ вернуть более одного значения ИСТИНА. На рис. 11.18 приведены данные, где есть три И критерия, при том что последний И критерий включает ИЛИ критерий: дата >= 18/03/2013 И дата 100 000 И чистая прибыль >= 37 500 И (рейтинг 1 >= 3,5 ИЛИ рейтинг2 >= 6). В конкретной ячейке логический тест ИЛИ может вернуть более одного значения ИСТИНА. Логический тест ИЛИ указывает на несколько столбцов.
Рис. 11.19. Критерии И, ИЛИ, когда логический тест ИЛИ указывает на несколько столбцов
Этот пример иллюстрирует пользу от вспомогательного столбца, в котором удобно разместить логический тест. Благодаря этому формула [1] выглядит предельно простой. Если вы хотите обойтись без вспомогательного столбца, вы можете использовать формулы [2], [3] или [4]. Обратите внимание, что определения максимального и среднего значения (формулы [5] и [6]) в качестве фильтра использована функция ЕСЛИ (одинаковая для обеих формул). В аргумент лог_выражение функции ЕСЛИ помещен фрагмент формулы: (B2:B7>B10)*(E2:E7>D10)* ((C2:C7>=C10)+(D2:D7>=C12)). Обратите внимание, что здесь есть два умножения (для операторов И) и одно сложение (для оператора ИЛИ). Такого рода логические структуры типичны для критериев И, ИЛИ.
Имейте в виду, что если формулы вам не нужны, для обработки критерия ИЛИ можно использовать фильтр, расширенный фильтр и сводные таблицы, подобно тому, как показано на рис. 11.2–11.5.




 .
.

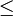 (меньше или равно).
(меньше или равно).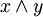 )
) 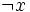 )
)