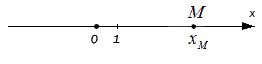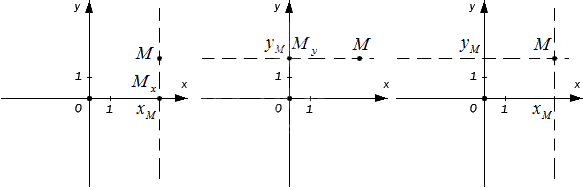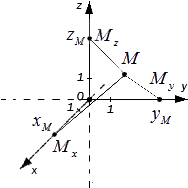Что такое декартовые координаты заданной точки
Декартовы координаты на плоскости и в пространстве
Декартовы координаты — это (декартова система координат) система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты.
Содержание:
Декартовы координаты на прямой
В курсе алгебры постоянно приходится пользоваться прямоугольной системой координат. Рассмотрим прямоугольную систему координат на прямой. Хорошей иллюстрацией этой системы координат является термометр.
Стрелка показывает положительное направление отсчета координат. Прямую с установленной на ней системой координат называют координатной прямой. Точку О называют началом координат. Кроме этого, на координатной прямой вводится единичный отрезок ОЕ, его иногда называют масштабом.
Декартовы координаты на плоскости
Положение точки на плоскости может быть определено ее расстоянием до двух фиксированных взаимно перпендикулярных прямых — осей. В этом случае каждой точке плоскости будет соответствовать не одно число, а пара чисел. Соответствие между точками и парами чисел задается на плоскости: выбирают прямую, называемую осью Ох, вводят на ней систему координат. На оси Ох рисуют стрелку, чтобы указать ее положительное направление. Эта ось называется также осью абсцисс.
Проводят прямую Оу, перпендикулярную оси Ох и проходящую через точку О прямой Ох, имеющую координату 0, и вводят на прямой Оу систему координат так, чтобы точка с координатой 0 совпадала с точкой О. Прямая Оу называется осью Оу или осью ординат. Положительное направление на оси Оу также указывается стрелкой. Точка О пересечения прямых Ох и Оу (осей координат) называется началом координат (рис. 2.445).
На рисунке 2.446 изображена построенная прямоугольная система координат. Если дана точка Р, то из нее опускают перпендикуляр на ось Ох. Пусть основанием перпендикуляра будет точка М и х — координата точки М на прямой Ох (рис. 2.446). Тогда число х называют абсциссой точки Р. На рисунке 2.446 
Затем опускают из точки Р перпендикуляр на ось Оу. Пусть основанием этого перпендикуляра будет точка N и у — координата точки N на прямой Оу. Тогда число у называют ординатой точки Р. На рисунке 2.446 

Порядок, в котором записываются координаты точки, очень существенен. Координаты (1, 3) имеет точка 

Ниже приводится определение координат точки на плоскости.
Определение. Абсциссой точки Р называют координату основания перпендикуляра, опущенного из точки Р на ось Ох; ординатой точки Р называют координату основания перпендикуляра, опущенного из точки Р на ось Оу.
Если прямая разбивает плоскость на две полуплоскости, то две оси координат разбивают плоскость на четыре части, называемые четвертями. Четыре четверти нумеруются в порядке, изображенном на рисунке 2.448.
Таким образом, между точками плоскости и упорядоченными парами действительных чисел имеется взаимооднозначное соответствие. Такое соответствие называют прямоугольной системой координат.
Декартовы координаты в пространстве
Построим горизонтальную плоскость и введем на ней декартову систему координат хОу (рис. 2.449).
Если ввести также координатную прямую Oz, перпендикулярную плоскости хОу в точке О, то тем самым будет введена система координат в пространстве. Точка О будет началом этой системы координат.
Стрелки осей Ох, Оу и Oz на рисунках указывают положительное направление каждой оси.
В декартовой системе координат в пространстве мы имеем три оси: Ох — ось абсцисс, Оу — ось ординат, Oz — ось аппликат. Плоскости, проходящие через оси Ох и Оу, Оу и Oz, Ох и Oz — координатные плоскости. Их обозначают соответственно: ху, yz, xz (рис. 2.450). Координатные плоскости разбивают все пространство на восемь частей — октантов.
Если задана такая система координат, то каждой точке пространства можно поставить в соответствие упорядоченную тройку действительных чисел, а каждой тройке чисел — единственную точку.
На рисунке 2.452: точка Р лежит в плоскости хОу, так что ее проекция на ось Ог есть 0. Ее проекция на ось Ох совпадает с точкой, имеющей координату 2, а на ось Оу — с точкой, имеющей координату 3. Поэтому пишут Р(2, 3, 0).
Таким образом, нахождение координат точки в пространстве сводится к построению соответствующего прямоугольного параллелепипеда (иногда его воспроизводят частично, чтобы были видны координаты точки (рис. 2.453)).
Порядок записи этих трех чисел также существенен. На рисунке 2.452 изображены точки 
Можно иначе находить координаты точки пространства. Пусть дана точка М. Спроектируем точку М на оси Ох, Оу, Ог в точки 

Если есть три координаты — три числа 



Прямоугольная система координат носит имя Рене Декарта (1596—1650). В 1637 г. вышла книга с длинным по обычаю времен названием «Рассуждение о методе, позволяющем направлять разум и отыскивать истину в науках. Кроме того, Диоптрика, Метеоры и Геометрия, которые являются приложениями этого метода», с ней в науку вошел метод координат. Со времен Декарта алгебра и геометрия стали сотрудничать между собой к выгоде обеих дисциплин. Введенную систему координат с тех пор стали называть декартовой.
Координаты середины отрезка
Рассмотрим отрезок 



1. 
2. 
3. 
Эта формула годится и в случае, когда
Рассмотрим случай, когда отрезок 
1. Точка Р является серединой отрезка 
2. Построим проекции точек 

3. Точка М является серединой отрезка 
4. 
Аналогично можно получить, что 
Теорема 1. Даны точки 

Формула расстояния между точками
Пусть мы знаем координаты двух точек 
Теорема 2. Расстояние между точками 
Например, если 
Формула расстояния между точками верна и в пространстве. Пусть даны две точки 

Пример:
Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от его вершин.
Решение:
Из условия задачи имеем:
1. 
3. CD = AD (требуется доказать).
Мы хотим применить для решения задачи декартову систему координат, а значит, надо удачно выбрать расположение этой системы.
4. Для данной задачи удачный выбор системы координат показан на рисунке 2.460. Начало координат помещено в точку А, а оси проведены через точки Б и С так, чтобы эти точки лежали на положительных лучах осей (построение).
5. Точка В имеет координаты (

6. Середина отрезка СВ точка D имеет координаты 
7. 
8. 
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Прямоугольная система координат на плоскости и в пространстве
При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.
Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.
Прямоугольная декартова система координат на плоскости
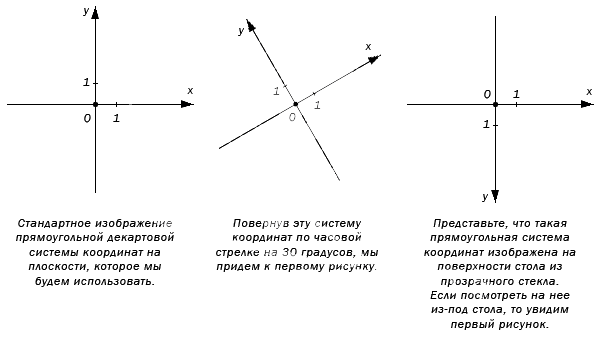
Изображение прямоугольной системы координат на плоскости.
Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.
Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.
Прямоугольная система координат в трехмерном пространстве
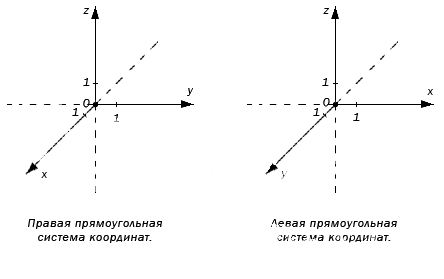
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.
Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат на плоскости
Имеющееся число x M называют координатой точки М на заданной координатной прямой.
Координаты точки в прямоугольной системе координат в трехмерном пространстве
Декартова система координат: основные понятия и примеры
Понятие декартовой системы координат
С именем французского математика Рене Декарта (1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат (аффинная система координат). Она может включать и не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является прямоугольной.
Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.
Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.
Прямоугольная декартова система координат на плоскости
Координатные оси разбивают плоскость на четыре квадранта, нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.
Прямоугольная декартова система координат в пространстве
Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.
Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.
Задачи о точках в декартовой системе координат
Пример 1. В декартовой системе координат на плоскости даны точки
Найти координаты проекций этих точек на ось абсцисс.
Пример 2. В декартовой системе координат на плоскости даны точки
Найти координаты проекций этих точек на ось ординат.
Пример 3. В декартовой системе координат на плоскости даны точки
Решить задачи на декартову систему координат самостоятельно, а затем посмотреть решения
Пример 5. В декартовой системе координат на плоскости даны точки
Продолжаем решать задачи вместе
Пример 6. В декартовой системе координат на плоскости даны точки
Пример 7. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно начала координат.
Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:
Пример 8. В декартовой системе координат в пространстве даны точки
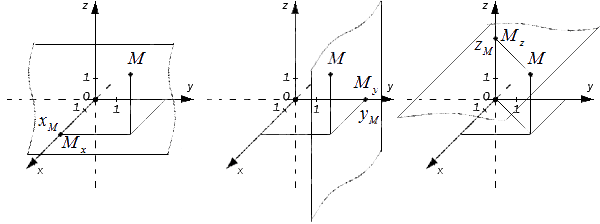
Найти координаты проекций этих точек:
1) на плоскость Oxy ;
2) на плоскость Oxz ;
3) на плоскость Oyz ;
1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy :
2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz :
3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz :
Пример 9. В декартовой системе координат в пространстве даны точки
Найти координаты точек, симметричных этим точкам относительно:
7) начала координат.
По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.
4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:
5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:
6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:
7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат:
Декартовы координаты
Прямоугольная, или декартова система координат — наиболее распространённая система координат на плоскости и в пространстве.
Содержание
Прямоугольная система координат на плоскости
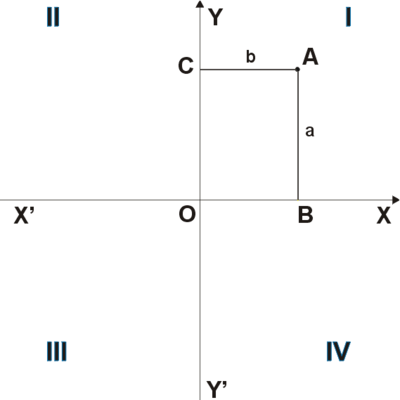
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве
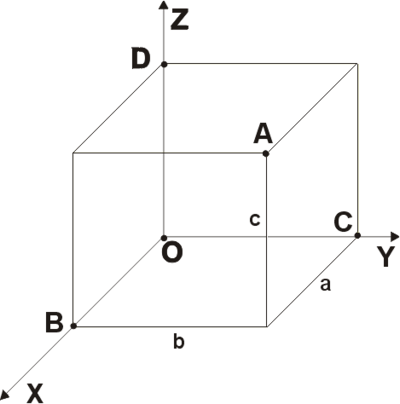
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
История
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
См. также
Ссылки
Полезное
Смотреть что такое «Декартовы координаты» в других словарях:
ДЕКАРТОВЫ КООРДИНАТЫ — (декартова система координат) система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты. Названы по имени Р. Декарта … Большой Энциклопедический словарь
декартовы координаты — Система координат, состоящая из двух перпендикулярных осей. Положение точки в такой системе формируется с помощью двух чисел, определяющих расстояние от центра координат по каждой из осей. [http://www.morepc.ru/dict/] Тематики информационные… … Справочник технического переводчика
декартовы координаты — (декартова система координат), система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты. Названы по имени Р. Декарта … Энциклопедический словарь
декартовы координаты — Dekarto koordinatės statusas T sritis Standartizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: angl. Cartesian coordinates vok. kartesische Koordinaten, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
декартовы координаты — Dekarto koordinatės statusas T sritis fizika atitikmenys: angl. Cartesian coordinates; grid coordinates vok. kartesische Koordinaten, f rus. декартовы координаты, f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas
ДЕКАРТОВЫ КООРДИНАТЫ — способ определения положения точек на плоскости их расстояниями до двух фиксированных перпендикулярных прямых осей. Это понятие усматривается уже у Архимеда и Аппология Пергского более двух тысяч лет назад и даже у древних египтян. Впервые эта… … Математическая энциклопедия
ДЕКАРТОВЫ КООРДИНАТЫ — декартова система координат [по имени франц. философа и математика Р. Декарта (R. Descartes; 1596 1650)], система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные Д … Большой энциклопедический политехнический словарь
ДЕКАРТОВЫ КООРДИНАТЫ — (декартова система координат), система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные Д. к. Названы по имени Р. Декарта … Естествознание. Энциклопедический словарь
ДЕКАРТОВЫ КООРДИНАТЫ — Система расположения любой точки нашли кости относительно двух осей, перекрещивающихся под прямым углом. Разработанная Рене Декартом, эта система стала основой для стандартных методов графического представления данных. Горизонтальная линия… … Толковый словарь по психологии
Координаты — Координаты. На плоскости (слева) и в пространстве (справа). КООРДИНАТЫ (от латинского co совместно и ordinatus упорядоченный), числа, которые определяют положение точки на прямой, плоскости, поверхности, в пространстве. Координаты суть расстояния … Иллюстрированный энциклопедический словарь