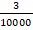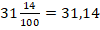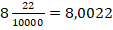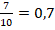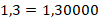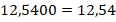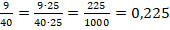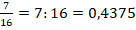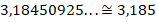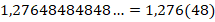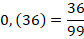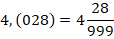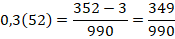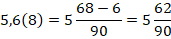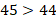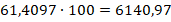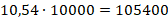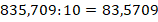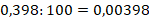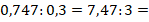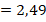Что такое десятичная запятая
Десятичная запятая
Имеет особую форму записи: целая часть в десятичной системе счисления, затем запятая и затем дробная часть в десятичной системе счисления, причём количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.
| обыкновенная дробь | десятичная дробь |
|---|---|
| 4 /10 | 0,4 |
| 79 395 /1000 | 79,395 |
Очевидно, в начало целой части и/или в конец дробной части можно дописывать сколько угодно нулей.
Существуют также бесконечные десятичные дроби — периодические и непериодические. Например, ⅓ записывается как бесконечная периодическая дробь 0,3333… или 0,(3). А число π записывается как бесконечная непериодическая дробь 3,141592…
Периодическая десятичная дробь называется чистой периодической дробью, если её период (группа повторяющихся цифр) начинается сразу после запятой, а период может содержать любое конечное число цифр. Так, дробь 1,(3) — чистая периодическая дробь. Если периодическая десятичная дробь содержит ещё число, заключённое между целой частью и периодом, то такая периодическая дробь называется смешанной; число периодической дроби, стоящее между целой частью и периодом, называется предпериодом этой дроби.
Очевидно, что всякая периодическая дробь является рациональным числом вида 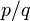
Произношение десятичных дробей
В русском языке десятичные дроби читаются так: сначала произносится целая часть, потом слово «целых» («целая»), потом десятичная часть так, как если бы всё число состояло только из этой части, то есть числитель дроби — количественное числительное женского рода (одна, две, восемь и т. д.), а знаменатель — порядковое числительное (седьмая, сотая, двести тридцатая и т. д.).
Однако на практике часто встречается такое произношение: целая часть, союз «и», дробная часть.
Десятичный разделитель
Десятичный разделитель — знак, используемый для разделения целой и дробной частей вещественного числа в форме десятичной дроби в системе десятичного исчисления. Для дробей в иных системах счисления может использоваться термин разделитель целой и дробной частей числа. Иногда также могут употребляться термины десятичная точка и десятичная запятая.
В англоязычных странах в качестве десятичного разделителя используется точка, в большинстве остальных — запятая (,).
Выбор символа для десятичного разделителя влияет и на выбор знака разделителя групп разрядов, который используется для того, чтобы упростить чтение больших чисел. Например, в русскоязычной среде в качестве этого разделителя принято использовать точку (.) или пробел.
Содержание
История вопроса
В Средние века, в допечатную эпоху было принято надчёркивать (¯) целую часть числа. Таким способом пользовался, например, иранский математик ал-Хорезми. Позже для этих целей стал применяться небольшой вертикальный штрих (ˌ) (символ U+02CC). Уже после начала книгопечатания этот штрих стало естественным отображать либо точкой, либо запятой. Большинство стран выбрали в качестве десятичного символа запятую. Однако англоязычные страны предпочли точку, а запятую стали использовать как разделитель групп разрядов.
В США в качестве десятичного разделителя использовалась точка. В Британской империи в рукописной записи также использовали точку, однако в типографском наборе предпочтительнее был интерпункт — точка, расположенная на середине строки (·). Но такой символ уже был общеупотребительным в математике для обозначения операции умножения, и система СИ не допускала его использования в качестве разделителя. В то же время использование точки допускалось. Поэтому в Британии постепенно переняли американскую систему.
В ЮАР при принятии метрической системы в качестве разделителя стали использовать запятую, заменив принятую в бывших британских колониях точку.
В большинстве международных организаций (таких, как Международное бюро мер и весов и ISO) до 1997 года во всех языках, включая английский, в качестве десятичного разделителя рекомендовалось использовать только запятую. Затем постепенно начался процесс признания точки в качестве десятичного разделителя, увенчавшийся принятием в 2003 году нормы ISO 31-0, допускающей использование как точки, так и запятой.
В арабских странах в качестве десятичного разделителя используется особый символ моммайе: «٫» (U+066B).
Разделитель групп разрядов
Для упрощения чтения, цифры в больших числах слева (а иногда и справа) от знака десятичного разделителя могут быть разделены на группы специальным символом — разделителем групп разрядов. Разбивка на группы осуществляется начиная от десятичного разделителя. Как правило, группы состоят из трёх цифр. В то же время в некоторых странах числа традиционно делятся на группы из двух или четырёх цифр. Деление на группы, как правило, не осуществляется, если с соответствующей стороны от десятичного разделителя не больше четырёх или пяти цифр.
Так же, как и в случае с десятичным разделителем, для разделителя групп разрядов используются разные символы. Если в качестве десятичного разделителя используется точка, то разделитель групп разрядов может быть представлен запятой, апострофом или пробелом, а если запятая, — то точкой (например, в испанском языке [1] [2] ) или пробелом. Таким образом, значение точки и запятой оказывается зависимым от контекста (например, запись 1,546 в английской нотации обозначает тысяча пятьсот сорок шесть, а в русской — одна целая пятьсот сорок шесть тысячных). Поэтому, чтобы избежать неоднозначности, для разделителя групп разрядов международные стандарты (ISO, Международное бюро мер и весов, ИЮПАК) рекомендуют всегда использовать пробел (или тонкую шпацию при типографском наборе).
Десятичные разделители в разных странах
| Австралия и Океания | Америка | Азия | Африка | Европа |
|---|---|---|---|---|
| Австралия, Новая Зеландия | Англоязычная Канада, Мексика, США | Бруней, Израиль, Индия, Китай, КНДР, Малайзия, Пакистан, Сингапур,Тайвань, Таиланд, Филиппины, Шри Ланка, Южная Корея, Япония | Ботсвана, Зимбабве, Нигерия | Великобритания, Ирландия |
| Австралия и Океания | Америка | Азия | Африка | Европа |
|---|---|---|---|---|
| — | Вся Южная Америка, кроме Перу, а также Гватемала, Гондурас, Доминиканская республика, франкоязычная Канада, Куба, Никарагуа, Панама, Сальвадор | Вьетнам, Индонезия, Турция | Камерун, ЮАР | Вся Европа, кроме Великобритании и Ирландии, а также все страны бывшего СССР |
| А также в искусственных языках интерлингва и эсперанто. | ||||
| Австралия и Океания | Америка | Азия | Африка | Европа |
|---|---|---|---|---|
| — | — | Бахрейн, Иран, Ирак, Катар, Кувейт, ОАЭ, Оман, Саудовская Аравия, Сирия | — | — |
Распространение систем обозначений
Все страны, использующие в качестве десятичного разделителя запятую, знакомы и с англоязычной нотацией из-за того, что такая система используется во многих электронных устройствах, например, калькуляторах.
Большинство операционных систем позволяют пользователю выбрать предпочтительные символы для десятичного разделителя и для разделителя групп разрядов, и программное обеспечение может учитывать этот выбор.
В большинстве языков программирования в качестве десятичного разделителя используется точка, а при разработке языка Алгол между разработчиками разыгралась «десятичная буря» (см. в статье о языке Алгол): европейцы требовали выбрать запятую, а американцы — точку.
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
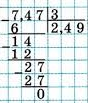
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Десятичная дробь
Десятичные дроби: определение, сложение, вычитание, умножение, деление, сравнение
Десятичная дробь является частным случаем обыкновенных дробей (у которой знаменатель кратен 10).
Определение
Десятичными называют дроби, знаменатели которых представляют собой числа, состоящие из единицы и некоторого количества следующих за нею нулей. То есть это дроби со знаменателем 10, 100, 1000 и т.д. Иначе десятичную дробь можно охарактеризовать как дробь со знаменателем 10 или одной из степеней десятки.
 ,
,  ,
, 
Десятичная дробь записывается иначе, чем обыкновенная. Операции с этими дробями также отличны от операций с обыкновенными. Правила действий над ними в значительной мере приближены к правилами действий над целыми числами. Этим, в частности, обусловлена их востребованность при решении практических задач.
Представление дроби в десятичной записи
В записи десятичной дроби нет знаменателя, в ней отображено число числителя. В общем виде запись десятичной дроби осуществляется по такой схеме:
где Х – целая часть дроби, Y – ее дробная часть, «,» – десятичная запятая.
Для правильного представления обыкновенной дроби в виде десятичной требуется, чтобы она была правильной, то есть с выделенной целой частью (если это возможно) и числителем, который меньше знаменателя. Тогда в десятичной записи целая часть записывается до десятичной запятой (Х), а числитель обыкновенной дроби – после десятичной запятой (Y).
Если в числителе представлено число с количеством знаков, меньшим, чем количество нулей в знаменателе, то в части Y недостающее количество знаков в десятичной записи заполняется нулями впереди цифр числителя.
Пример:
Если обыкновенная дробь меньше 1, т.е. не имеет целой части, то для Х в десятичном виде записывают 0.
В дробной части (Y), после последнего значимого (отличного от нуля) разряда, может быть вписано произвольное количество нулей. На значение дроби это не влияет. И наоборот: все нули в конце дробной части десятичной дроби можно опустить.
Прочтение десятичных дробей
Часть Х читается в общем случае так: «Х целых».
Часть Y прочитывается в соответствии с числом в знаменателе. Для знаменателя 10 следует читать: «Y десятых», для знаменателя 100: «Y сотых», для знаменателя 1000: «Y тысячных» и так далее… 😉
Более корректным считается другой подход к прочтению, основанный на подсчете количества разрядов дробной части. Для этого нужно понимать, что дробные разряды расположены в зеркальном отражении по отношению к разрядам целой части дроби.
Наименования для правильного прочтения приведены в таблице:
Исходя из этого, прочтение должно опираться на соответствие наименованию разряда последней цифры дробной части.
Перевод произвольной обыкновенной дроби в десятичную
Если в знаменателе обыкновенной дроби стоит 10 или какая-нибудь степень десятки, то перевод дроби выполняется как описано выше. В остальных ситуациях необходимы дополнительные преобразования.
Существует 2 способа перевода.
Первый способ перевода
Числитель и знаменатель необходимо домножить на такое целое число, чтобы в знаменателе было получено число 10 или одна из степеней десятки. А далее дробь представляется в десятичной записи.
Этот способ применим для дробей, знаменатель которых раскладывается только на 2 и 5. Так, в предыдущем примере 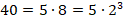
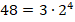
Второй способ перевода
2-й способ заключается в делении числителя на знаменатель в
Правило деления в столбик, приводящее в результате к десятичной дроби, описано ниже (см. Деление десятичных дробей).
Перевод десятичной дроби в обыкновенную
Для этого следует ее дробную часть (справа от запятой) записать в виде числителя, а результат прочтения дробной части – в виде соответствующего числа в знаменателе. Далее, если это возможно, нужно сократить полученную дробь.
Конечная и бесконечная десятичная дробь
Конечной называют десятичная дробь, дробная часть которой состоит из конечного количества цифр.
Выше все приведенные примеры содержат именно конечные десятичные дроби. Однако не всякую обыкновенную дробь возможно представить в виде конечной десятичной. Если 1-й способ перевода для данной дроби не применим, а 2-й способ демонстрирует, что деление невозможно завершить, значит, получена может быть только бесконечная десятичная дробь.
В полном виде бесконечную дробь записать невозможно. В неполном же виде такие дроби можно представить:
Периодической называется дробь, у которой после запятой можно выделить повторяющуюся бесконечно последовательность цифр.
Остальные дроби называются непериодическими. Для непериодических дробей допустим только 1-й способ представления (округление).
Пример периодической дроби: 0,8888888… Здесь налицо повторяющаяся цифра 8, которая, очевидно, будет повторяться до бесконечности, поскольку нет оснований предполагать иное. Эта цифра называется периодом дроби.
Периодические дроби бывают чистыми и смешанными. Чистой является десятичная дробь, у которой период начинается непосредственно после запятой. У смешанной дроби до периода после запятой имеется 1 или больше цифр.
54,33333… – периодическая чистая десят.дробь
2,5621212121… – периодическая смешанная дробь
Примеры записи бесконечных десятичных дробей:
Во 2-м примере показано, как правильно оформлять период в записи периодической дроби.
Перевод периодических десятичных дробей в обыкновенные
Для перевода чистой периодической дроби в обыкновенную ее период записывают в числитель, а в знаменатель пишут число, состоящее из девяток в количестве, равном количеству цифр в периоде.
Смешанная периодическая десятичная дробь переводится следующим образом:
Сравнение десятичных дробей
Десятичные дроби сравнивают первоначально по их целым частям. Больше та дробь, у которой больше ее целая часть.
Если целые части одинаковы, то сравнивают цифры соответствующих разрядов дробной части, начиная с первого (с десятых). Здесь действует тот же принцип: больше та из дробей, у которой больше разряд десятых; при равенстве цифр разряда десятых сравнивают разряды сотых и так далее.
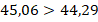
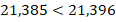
Сложение и вычитание десятичных дробей
Десятичные дроби складывают и вычитают так же, как и целые числа, записав соответствующие цифры друг под другом. Для этого нужно, чтобы друг под другом находились десятичные запятые. Тогда единицы (десятки и т.д.) целой части, а также десятые (сотые и т.д.) дробной окажутся в соответствии. Недостающие разряды дробной части заполняют нулями. Непосредственно процесс сложения и вычитания осуществляется так же, как и для целых чисел.
Примеры:
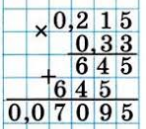
Умножение десятичных дробей
Для умножения десятичных дробей нужно записать их друг под другом, выровняв по последней цифре и не обращая внимания на местоположение десятичных запятых. Затем нужно перемножить числа так же, как и при умножении целых чисел. После получения результата следует пересчитать количество цифр после запятой в обоих дробях и отделить запятой в результирующем числе суммарное количество дробных разрядов. Если разрядов не хватает, то они заменяются нулями.
Умножение и деление десятичных дробей на 10 n
Примеры:
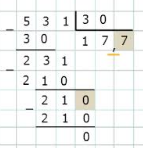
Деление десятичной дроби и целого числа на целое число и на десятичную дробь
Деление в столбик десятичной дроби на целое число выполняется аналогично делению двух целых чисел. Дополнительно требуется только учет положения десятичной запятой: при сносе цифры разряда, за которым следует запятая, необходимо поставить запятую после текущей цифры формируемого ответа. Далее нужно продолжать делить до получения нуля. Если знаков в делимом для полного деления недостает, в их качестве следует использовать нули.
Аналогично делятся в столбик 2 целых числа, если снесены все цифры делимого, а полное деление еще не завершено. В этом случае после сноса последней цифры делимого ставится десят.запятая в формирующемся ответе, а в качестве сносимых цифр используют нули. Т.е. делимое здесь, по сути, представляют как десятичную дробь с нулевой дробной частью.
Пример:
Графическое представление десятичных дробей
Графически десятичные дроби изображаются посредством координатной прямой. Для этого единичные отрезки делят дополнительно на 10 равных долей подобно тому, как на линейке откладываются одновременно сантиметры и миллиметры. Это обеспечивает точное отображение десятичных дробей и возможность объективного их сравнения.
Чтобы дольные деления на единичных отрезках были одинаковыми, следует тщательно продумывать длину самого единичного отрезка. Она должна быть такой, чтобы можно было обеспечить удобство дополнительного деления.



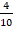 ,
, 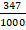 ,
,