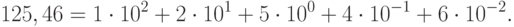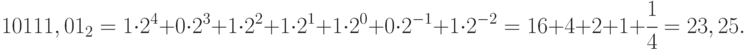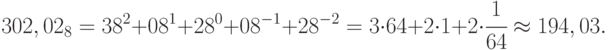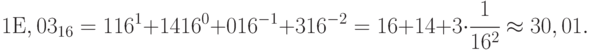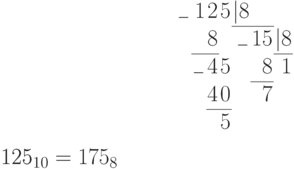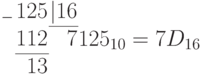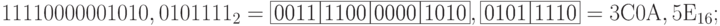Что такое десятичный эквивалент числа

Перевод чисел из одной системы счисления в другую

Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.

Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.

Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
200₁₀ = 11001000₂ = 310₈ = C8₁₆

Кратко об основных системах счисления

Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.

Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.

Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.

Перевод в десятичную систему счисления

Перевод из десятичной системы счисления в другие

Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.

Переведем число 375₁₀ в восьмеричную систему:

Перевод из двоичной системы в восьмеричную

Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:

Перевод из двоичной системы в шестнадцатеричную

Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:

Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Перевод из восьмеричной системы в двоичную

Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.

Используем таблицу триад:

Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.

Перевод из шестнадцатеричной системы в двоичную

Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.

Используем таблицу тетрад:

Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111

Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.

Перевод из восьмеричной системы в шестнадцатеричную и наоборот

Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.

Источник

Как записать десятичный эквивалент числа

Вычислите десятичные эквиваленты следующих двоичных чи-
сел:
111₂
1010₂
11011₂
101101₂

так надо написать на 5

Здравствуйте! На рисунке изображён график функции у =f(х). Точки a, b, с, d и е задают на оси х четыре интервала. Помогите пользуясь ( Подробнее. )

2. В чем заключается принцип Ферма?

Плата за телефон составляет 350 рублей в месяц. В следующем году она увеличится на 12%. Сколько рублей придётся платить ежемесячно за ( Подробнее. )

Приведите примеры информации, которая в конкретной ситуа-
ции является:
актуальной (своевременной)/неактуальной ( Подробнее. )

От разведчика была получена шифрованная радиограмма, пере-
данная с использованием азбуки Морзе. При передаче радио-
граммы ( Подробнее. )

Ответ оставил Гуру

Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Информатика.

Помогите записать десятичные эквиваленты чисел, не понимаю как это сделать.172 (8) (восьмёрка в учебнике записана маленьким шрифтом внизу) 2EA(16) 101010(2) 10,1(2) 243(6)

Лучший ответ:

Цифры записанные внизу указывают систему счисления
172₈ – число записано в восьмеричной системе счисления. Требуется перевести его в десятичной системе счисления.
172₈ = 1*8² 7*8¹ 2*8⁰ = 64 56 2 = 122₁₀ – т.е. 122 в десятичной
2ЕА₁₆ = 2*16² 14*16¹ 10*16⁰ = 512 224 10 = 746₁₀
101010₂ = 1*2⁵ 0*2⁴ 1*2³ 0*2² 1*2¹ 0*2⁰ = 32 0 8 0 2 0 = 42₁₀
10,1₂ = 1*2¹ 0*2⁰ 1*2⁻¹ = 2 0 1/2 = 2,5₁₀
243₆ = 2*6² 4*6¹ 3*6⁰ = 72 24 3 = 99₁₀

Источник

Десятичное число 1439 =

== двоично-десятичному числу 1010000111001 (3 нуля в начале опущены) Написание:

Написание числа 1439 в двоично-десятичной системе

5.3. Вычисление десятичного эквалента двоичного числа 10110011111

Вычисленный десятичный эквивалент

Буквы. Шестая и седьмая дорожки совместно с дорожками, предназначенными для кодирования цифр, используются для кодирования букв и специальных знаков. Рис. 5.7 показывает, что существует определенная система кодирования букв (английского) алфавита, хотя код ASCII несколько отличается от кода EIA244A. В коде ASCII алфавит кодируется пробиванием отверстий в шестой и седьмой дорожках с добавлением чисто двоичного кода номера буквы от 1 до 26 на дорожках с первой по пятую, поскольку в алфавите 26 букв. Код EIA244A следует двоично-десятичное системе счисления за счет разделения алфавита на три группы по десять букв. Группы кодируются следующим образом.

Буквы алфавита от А до I: отверстия в шестой и седьмой дорожках; буквы от J до R: отверстия в седьмой дорожке; буквы от S до Z: отверстия в шестой дорожке. Внутри группы цифры нумеруются с 1 до 9 в двоичной системе.

Внимательный читатель уже вероятно заметил некоторое несоответствие в описании процедуры кодирования букв в коде EIA244A. Ведь алфавит состоит из 26 букв, а не из 27, поэтому «три группы по девять букв» оставляют одну комбинацию неиспользованной. Сможете ли вы определить по рис. 5.7, какая комбинация пропущена и какому месту в алфавите это соответствует?

Проверка четности. Пятая дорожка в коде EIA244A и восьмая дорожка в коде ASCII зарезервированы для проверки надежности перфоратора и устройства считывания программы, установленного на станке. По установленному жесткому правилу число отверстий в каждом горизонтальном ряду всегда должно быть четным (в случае кода EIA244A) или нечетным (в случае кода ASCII). Это правило называется проверкой четности (или нечетности в зависимости от кода). Поскольку некоторым знакам двоично-десятичного кода соответствует четное количество отверстий, а некоторым — нечетное, дорожка четности используется для добавления в случае необходимости отверстия, обеспечивающего четность (или нечетность) каждого горизонтального ряда. Цель этой операции сейчас будет объяснена.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Двоичные числа и двоичная арифметика

Принцип представления чисел в позиционных системах счисления

Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].

сотни десятки единицы десятые доли сотые доли

Аналогично любое число в десятичной системе счисления можно представить в виде подобной суммы:

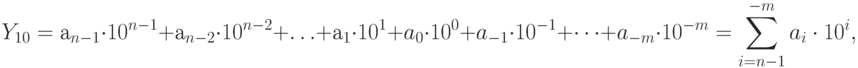( 11.1)

Для числа в системе счисления с основанием выражение (11.1) преобразуется к виду:

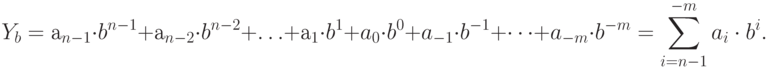( 11.2)

Таблица 11.1. Параметры позиционных систем счисления

Название системы счисления	Основание системы счисления	Знаки, использующиеся для записи чисел
Двоичная	2	0, 1
Троичная	3	0, 1, 2
Четверичная	4	0, 1, 2, 3
…	…	…
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7
…	…	…
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
…	…	…
Шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
…	…	…

Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).

Для двоичного числа:

Для восьмеричного числа:

Для шестнадцатеричного числа:

Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 11.2. Для нашего примера вместо знака » » в расчетную формулу (11.2) подставляется десятичное число .

Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.

Перевод чисел из одной системы счисления в другую

Перевод из десятичной системы в любую другую. Перевод целых чисел

Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.

Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).

В рассмотренном примере при переводе вместо коэффициента используется его десятичный эквивалент в соответствии с таблицей 11.2.

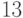
Перевод из двоичной системы в шестнадцатеричную (восьмеричную)

Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.

Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).

Таблица 11.2. Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков

Двоичная группа	Шестнадцатеричный знак	Десятичный эквивалент	Двоичная группа	Восьмеричный знак
0000	0	0	000	0
0001	1	1	001	1
0010	2	2	010	2
0011	3	3	011	3
0100	4	4	100	4
0101	5	5	101	5
0110	6	6	110	6
0111	7	7	111	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

Перевод из шестнадцатеричной (восьмеричной) системы в двоичную

Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).

Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.

Источник

Эквиваленты десятичных чисел в различных системах счисления

ALFA1 FECD 15AB BASIC

Все процессы, происходящие в вычислительной системе, связаны непосредственно с различными физическими носителями информационных сообщений (носитель данных), а все узлы и блоки этой системы являются физической средой, в которой осуществляются информационные процессы. Особенности носителя информации накладывают определённые ограничения

на используемый для её представления алфавит. При подготовке к решению на ЭВМ исходная формулировка, описание методов решения, задание конкретных исходных данных осуществляется на математическом языке, алфавит которого наряду с буквами естественного языка может включать буквы других языков, специальные символы математических операций и другие знаки. Носителем информации на данном этапе служат листы обычной бумаги.

Для ввода в ЭВМ информация об условиях задачи и методе её решения должна быть перенесена на специальный носитель, с которого она воспринимается в ЭВМ.

При единичном производстве компакт- дисков подложка выполняется из золота, а нанесение информации на неё осуществляется лучом лазера.

Носителем информации в электронных блоках ЭВМ, ведущих её обработку, является электрический сигнал, у которого меняется какой- либо параметр (частота, амплитуда).

Как видно из приведённых примеров, в процессе ввода, хранения, обработки и вывода информации в ЭВМ осуществляется неоднократное её преобразование из одной формы в другую. При этом с каждой из используемых форм представления информации связаны различные алфавиты. Процесс преобразования информации часто требует представлять буквы одного алфавита средствами (буквами, словами) другого алфавита. Такое представление называется кодированием. Декодированием называется процесс обратного преобразования информации относительно ранее выполненного кодирования.

Для представления информации в ЭВМ преимущественное распространение получило двоичное кодирование, при котором символы вводимой в ЭВМ информации представляются средствами двоичного алфавита, состоящего из двух букв. Это символы «0» и «1».

Двоичный алфавит по числу входящих в него символов является минимальным, поэтому при двоичном кодировании алфавита, включающего большое количество букв, каждой букве ставится в соответствие последовательность нескольких двоичных знаков или двоичное слово. Такие последовательности называются кодовыми комбинациями.

Полный набор кодовых комбинаций, соответствующих двоичному представлению всех букв кодируемого алфавита, называется кодом.

Различают коды равномерные и неравномерные. Кодовые комбинации равномерных двоичных кодов содержат одинаковое число двоичных знаков, неравномерных – не одинаковое.

Примером неравномерного двоичного кода может служить азбука Морзе, в которой для каждой буквы определена последовательность коротких и длинных сигналов. В азбуке Морзе букве Е, например, соответствует один короткий сигнал (точка), а букве Ш – четыре длинных сигнала (четыре тире). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающимся в передаваемых текстах символам назначается для их представления более короткая комбинация.

В технике наибольшее применение нашли равномерные коды, как более удобные для реализации. Например, во 2-м международном телеграфном коде символы передаваемого алфавита кодируются последовательностями из пяти «токовых или бестоковых посылок».

В вычислительной технике используются обычно равномерные коды, кодовые комбинации которых составляются последовательностью из восьми двоичных знаков. Такими являются, например, расширенный стандарт кодирования символов ASCII (American Standart Code for Information Interchange), модифицированная альтернативная кодировка ГОСТа, используемых в программах, работающих под управлением дисковой операционной системы (DOS) в компьютерах фирмы IBM.

Число символов, составляющих кодовую комбинацию, называется «длиной кода». В отношении двоичных кодов наряду с термином « длина кода» используется термин «разрядность кода».

Если разрядность кода обозначить через «n», то легко убедиться в том, что полное число кодовых комбинаций такого кода будет равно 2^n. Для ASCII n=8, а полное число кодовых комбинаций составляет 256. Модификация кода ASCII позволяет кодировать символы кириллицы.

Количество введённой в ЭВМ информации измеряют величиной, выраженной в двоичных знаках или битах. Бит – цифра 0 или 1.

Последовательность из восьми двоичных знаков, применяемая в используемых в вычислительной технике кодах для представления символов входных алфавитов получила название байт. Как правило, код символа хранится в одном байте, поэтому коды символов могут принимать значения от 0 до 255.Такие кодировки называются однобайтными, они позволяют использовать до 256 различных символов. Впрочем, в настоящее время всё большее распространение приобретает двухбайтная кодировка Unicode, в ней символы могут принимать значения от 0 до 65535. В этой кодировке имеются номера для практически всех применяемых символов (буквы алфавитов разных языков, математические, декоративные символы и т.д.). Используются и более крупные единицы количества информации: 1Килобайт = 1024 байт; 1Мегабайт = 1024Килобайт;

Названные единицы измерения количества информации используются для характеристики ёмкости запоминающих устройств ЭВМ. Ёмкость запоминающих устройств определяется количеством информации, которое хранится в памяти одновременно.

Например, в состав оборудования ЭВМ фирмы IBM входят накопители на жёстком диске ёмкостью 50Гигабайт. Персональные ЭВМ (ПК) комплектуются также накопителями на гибких магнитных дисках ёмкостью 720Кбайт, и1,44Мбайт, компакт – дисками ёмкостью 700Мбайт.

Для того, чтобы оценить порядок приведённых значений, определим, какой объём памяти необходим для хранения текста книги в 200 страниц, на каждой из которых размещены 50 строк по 50 символов. Простой подсчёт числа символов в книге даёт ответ на поставленный вопрос. Для хранения указанной книги необходимо запоминающее устройство ёмкостью 500 000 байт(50*50*200). Переведём полученное значение в Кбайты:

500 000 : 1024 = 488,2 Кбайт

Способность хранить и осуществлять быстрый поиск информации – важное качество вычислительных машин, обусловившее их широкое использование в системах автоматизированной обработки информации автоматического проектирования, в автоматизированных обучающих системах и т.д.

Размещение информации на гибких и жёстких дисках большого объёма позволяет отказаться от использования традиционной справочной и другой литературы. При наличии соответствующего оборудования пользователь может обеспечить доступ к локальной компьютерной сети организации или к глобальной сети Internet.

В информатике принято широко использовать понятие данные. Этот термин принято применять в отношении информации, представленной в формализованном (закодированном) виде, позволяющем хранить, передавать или обрабатывать её с помощью технических средств. Поэтому наряду с термином «ввод», «обработка», «хранение», «поиск информации» можно использовать термины ввод данных, обработка данных, хранение данных и т.п.

СИСТЕМЫ СЧИСЛЕНИЯ И ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ.

Необходимость выполнения арифметических действий над вводимыми в ЭВМ числами предъявляет особые требования к кодированию числовой информации. Язык чисел, как и обычный язык, имеет свой алфавит. В том языке чисел, которым сейчас пользуются практически на всём земном шаре, алфавитом служат десять цифр, от 0 до 9.Этот язык называется десятичной системой счисления. Однако не во все времена и не везде люди пользовались десятичной системой. С точки зрения чисто математической она не имеет специального преимущества перед другими возможными системами счисления и своим повсеместным распространением эта система обязана вовсе не общим законам математики, а причинам совсем иного характера. Десять пальцев на руке –первоначальный аппарат для счёта, которым человек пользовался, начиная с доисторических времён. Таким образом, именно счёт по пальцам положил начало той системе, которая кажется нам сейчас чем-то само собой разумеющимся. С момента создания цифровых вычислительных машин широкое распространение получила двоичная система счисления для двоичного представления чисел в ЭВМ, применяются также восьмеричная и шестнадцатеричная системы счисления.

Система счисления— это способ наименования и изображения чисел с помощью символов, имеющих определённые количественные значения (совокупность приёмов и правил записи чисел цифровыми знаками).

Любая предназначенная для практического применения система счисления должна обеспечивать:

— возможность представления любого числа в рассматриваемом диапазоне величин;

— единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);

— простоту оперирования с числами.

В зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные.

В позиционной системе счисления количественное значение каждой цифры зависит от её места (позиции) в числе: один и тот же знак принимает различные значения. Например, в десятичном числе 333 первая цифра справа означает три единицы, соседняя с ней – три десятка, а левая – три сотни.

Количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в пределах от 0 до Р-1.В общем случае запись любого смешанного числа в системе счисления с основанием Р будет представлять собой ряд вида:

где нижние индексы определяют местоположение цифры в числе (разряд):

— положительные значения индексов- для целой части числа (n разрядов);

— отрицательные значения- для дробной (s разрядов).

Компьютерная форма записи этого выражения будет:

Рассмотрим пример. Представим число 86,54 в соответствии с этой формулой:

86,54(10) = 8*10^1+ 6*10^0 + 5*10^(-1) + 4*10^(-2)

Для примера запишем число Х= 135(10) в двоичной, троичной, восьмеричной и шестнадцатеричной системах счисления.

Из приведённого примера видно, что увеличение основания системы счисления делает запись числа более компактной( уменьшает потребное количество разрядов для его изображения). В этом смысле наименее экономична двоичная система счисления. Количество разрядов в двоичной системе счисления примерно в 3,3 раза больше требуемого количества разрядов в десятичной системе счисления.

В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе.

Непозиционная система счисления – римская, в которой для каждого числа используется специфическое сочетание символов (XIV, CXXVII и т.п.)

В таблице приведены эквиваленты десятичных чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления.

Эквиваленты десятичных чисел в различных системах счисления.

Десятичное число Р =10	Двоичное число Р =2	Восьмеричное число Р =8	Шестнадцатеричное число Р =16
A
B
C
D
E
F

Системы счисления, применяемые в ЭВМ, можно разделить на основную и вспомогательные.

Основной является система счисления, в которой представляется и хранится информация, а также выполняются все основные операции в цифровой вычислительной машине. В качестве такой системы используется двоичная система счисления. Несмотря на громоздкость записи, она имеет перед другими системами счисления значительные преимущества. Это прежде всего простота конструкции элементов, представляющих каждый разряд числа.

При применении двоичной системы счисления они наиболее просты, так как должны иметь только два устойчивых состояния, соответствующих цифрам 0 и 1, которые изображают коэффициенты ai в нашей формуле. Это увеличивает надёжность функционирования ЭВМ. Простота выполненияарифметических операций является свойством двоичной арифметики.

При этом можно использовать хорошо разработанный аппарат двоичной логики.

Операции сложения, вычитания и умножения двоичных чисел представлены в таблице 2.

Двоичные операции
0+0=0	0-0=0	0*0=0
0+1=1	1-0=1	0*1=0
1+0=1	1-1=0	1*0=0
1+1=10	10-1=1	1*1=1
1+1+1=11

Операции сложения, вычитания, умножения и деления двоичных чисел выполняются по тем же правилам, которыми мы пользуемся при аналогичных действиях с десятичными числами. Рассмотрим это на примере.

Сложить два десятичных числа 15(10) и 17(10) в двоичной системе счисления:

Десятичное число 15(10) в двоичной системе счисления будет 1111(2), а десятичное число 17(10)=10001(2)

Сложение, как в десятичной системе счисления, выполним столбиком:

Сложение осуществляется следующим образом:

Сначала складываем две цифры младших разрядов 1+1

Результат равен 10 (2) В младшем разряде пишем 0, а 1 переносим во второй разряд. К имеющейся там 1 прибавляем перенесённую:

1+1 = 10, во втором разряде записываем 0, а 1 переносим в следующий старший (третий) разряд и т.д.

Проверку правильности операции можно провести, используя запись числа по формуле:

Умножение двоичных чисел производится в соответствии с таблицей 2.

Принцип умножения такой же, как и в десятичной системе счисления.

Пример 2: Получить произведение чисел Х1=10110(2) и Х2=1011(2) в двоичной системе счисления.

Деление двоичных чисел осуществляется многократным вычитанием делителя из делимого.Деление на произвольное число

Вспомним, как мы делим одно число на другое в десятичной системе исчисления. Я имеется в виду деление столбиком или углом. Точно так же происходит деление в двоичной системе. Вот пример деления двух двоичных чисел:

Сначала мы записываем делимое. В данном случае это число 1000001 (в десятичном виде 65). Затем, справа от него, рисуем угол. В верхней части угла записываем делитель. В нашем случае – это 101 (десятичное 5). Затем мы начинаем находить частное по разрядно. В десятичной системе исчисления в данном случае мы подбираем, на какое число от 1 до 9 нужно умножить делитель, для того, что бы результат был бы все же меньше, чем три первые разряда делимого. Если такого числа не находится, то берут первые четыре разряда делимого. В двоичной системе исчисления любой разряд может принимать только два значения – ноль или единица. Поэтому выбор у нас гораздо меньший. Делитель можно умножать только на 1 либо на ноль. При этом в первом случае он останется неизменным, а во втором он будет равен нулю. Нам придется лишь проверять не больше ли делитель, чем число, составляющее первые три разряда делимого. Как видим первые три разряда составляют число 100, что меньше, чем 101. Поэтому берем первые четыре разряда делимого. Число, составляющее первые четыре разряда делимого (1000) естественно больше делителя. Поэтому мы записываем делитель под первыми четырьмя разрядами делимого и вычитаем эти два числа. Получаем разность 11. В первый разряд частного записываем 1.

Находим следующий разряд частного. Для этого сносим следующий разряд делимого (так же, как это делается при делении в десятичной системе). Проверяем – можно ли теперь вычесть из него 101. Число 110 больше, чем 101. Поэтому мы записываем единицу в следующий разряд частного и производим вычитание этих двух чисел. Разность равна 1.

Далее ищем третий разряд частного. Сносим еще один ноль с очередного разряда делимого. Но из числа 10 невозможно вычесть 101. 10 меньше, чем 101. Поэтому записываем в очередной разряд частного ноль и сносим последний разряд делимого. Теперь вычитание возможно. Более того, результат вычитания равен нулю. Это означает во первых, что последний разряд частного равен единице, а во вторых то, что число 1000001 поделилось на 101 без остатка. Результат деления равен 1101 (десятичное 13).

Вспомогательные системы счисления используются для ввода и вывода информации, а также для перехода из одной системы счисления в другую. В качестве вспомогательных систем счисления применяются: десятичная, восьмеричная и шестнадцатеричная системы.

Исходная числовая информация и результаты решения представляются, как правило, в десятичной системе счисления. Программа часто кодируется в шестнадцатеричной системе счисления, имеющей компактную запись, и, вместе с тем, делающей простой перевод чисел в двоичную систему счисления.

Шестнадцатеричные цифры имеют 16 значений: от 0 до15; они записываются цифрами от 0 до 9, затем идёт буква А( обозначает число 10), буква В (обозначает11), и далее от С до F(со значениями от 12 до 15). Десятичные эквиваленты чисел представлены в таблице 1. Каждая шестнадцатеричная цифра соответствует комбинации четырёх двоичных, т.е. 4 битам (16=2^4). Любую шестнадцатеричную цифру можно записать с помощью двоичной тетрады: 1(16)=0001, 2(16)=0010, 3(16)=0011, …А(16)=1010….. F(16)= 1111

Если для записи программы применяется восьмеричная система, использующая для записи числа цифры от 0 до 7, каждой цифре соответствует 3 бита (8=2^3).

Использование двоичной системы счисления для ЭВМ связано с необходимость перевода вводимых в ЭВМ чисел в двоичную систему счисления и обратного преобразования числовых данных при выводе из ЭВМ. Эти преобразования осуществляются автоматически с использованием специально разработанных методов. Однако если потребуется ручной перевод при отладке программы, то его можно осуществить несколькими путями: для целых чисел, правильных дробей, произвольных чисел

Рассмотрим порядок перевода целых десятичных чисел из одной системы счисления в другую:

1. Разделить данное число на основание новой системы счисления. Остаток от деления даёт младший разряд числа в новой системе счисления;

2. Если частное от деления больше или равно основанию системы счисления, продолжить деление в соответствии с пунктом 1. Второй остаток даёт второй разряд числа и т.д.

3. Такое последовательное деление необходимо продолжать до получения целого частного, которое будет меньше основания системы счисления. Это частное будет старшим разрядом числа в новой системе счисления.

Перевести число 49(10) в двоичную систему счисления.

49:2=24 1 в остатке; эту 1 пишем в младший разряд.

24:2=12 0 в остатке, пишем его во второй разряд.

12:2=6 0 в остатке, пишем его в третий разряд.

6:2=3 0 в остатке, пишем его в четвёртый разряд.

3:2=1 и 1 в остатке, пишем эту единицу в пятый разряд и частное от деления( 3:2=1) пишем в шестой, старший разряд.

ПРИМЕР 4:Перевести число 1237(10) в шестнадцатеричную систему.

1237:16= 77 5 остаток 5 запишем в младший разряд;

77:16= 4 13 остаток 13 (в шестнадцатеричной системе счисления это D пишем во второй разряд, а частное 4 (77:16=4) пишем в старший разряд.

Зависимость между числами шестнадцатеричной системы счисления и эквивалентными им двоичными тетрадами представлены в таблице 1. Рассмотрим перевод числа этим способом.

Перевести число 4D5(16) в двоичную систему счисления.

РЕШЕНИЕ: записываем каждую шестнадцатеричную цифру двоичными тетрадами, сохраняя при этом последовательность цифр шестнадцатеричного числа.

Для перевода двоичного числа в шестнадцатеричное необходимо разбить двоичное число на тетрады справа налево. Первую цифру двоичного числа при необходимости дополняют до тетрады нулями.

ПРИМЕР 6: перевести двоичное число 1011101110(2) в шестнадцатеричную систему счисления.

РЕШЕНИЕ: разобьём двоичное число на тетрады:

10 1110 1110 Неполную тетраду 10 дополни до четырёх знаков нулями ( получим 0010). Таким образом, получим

0010 1110 1110 четырёхбитовые группы, тетрады. Из таблицы 1 знаем их шестнадцатеричные эквиваленты. Получим 2 Е Е

Для перевода правильных дробей из системы счисления с основанием р1 в систему с основанием р2 используется метод, базирующийся на умножении переводимой правильной дроби на основание р2 новой системы счисления.

Рекомендуется следующая последовательность операций:

1. Умножить число на основание новой системы счисления;

2. В полученном произведении выделить целую часть. Она даст старший разряд дробной части нового искомого числа;

3. Дробную часть произведения снова умножить на основание новой системы счисления. Целая часть произведения даст следующий разряд нового числа и т.д.

При переводе правильных дробей точный перевод может потребовать значительного (иногда бесконечного) количества разрядов нового числа. Поэтому в большинстве случаев он осуществляется с определённой, заранее заданной точностью. Для этого в условии задачи указывается необходимое число разрядов нового числа, которое обеспечит точность представления числа в новой системе счисления примерно такую же, как и в исходной. В ЭВМ точность перевода обычно ограничивается длиной разрядной сетки, отведённой для представления чисел.

ПРИМЕР 7: Перевести число Х=0,2(10) в двоичную систему счисления с точностью до четырёх разрядов после запятой.

Целая часть Старший разряд

0,8*2= 1,6 1, следующий разряд 1

0,6*2= 1,2 1, следующий разряд 1

ОТВЕТ: 0,2(10) = 0, 0011(2)

Для перевода неправильных дробей из одной системы в другую систему счисления необходим раздельный перевод целой и дробной частей по правилам, описанным выше. Полученные результаты записывают в виде новой дроби в системе с основанием р2.

ПРИМЕР 8: перевести десятичное число Х=49,2(10) в двоичную систему счисления с точностью до четырёх разрядов после запятой.

Решение: Результаты перевода соответственно целой и дробной частей возьмём из примеров 3 и 7

ОТВЕТ: Х=49,2(10) = 110001,0011(2)

В информатике и вычислительной технике разработано множество других методов перевода чисел из одной системы счисления в другую, позволяющих получить результат с меньшими затратами времени на преобразования.

Источник