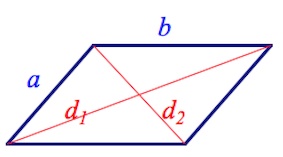
Что такое диагональ параллелограмма
Параллелограмм. Формулы, признаки и свойства параллелограмма
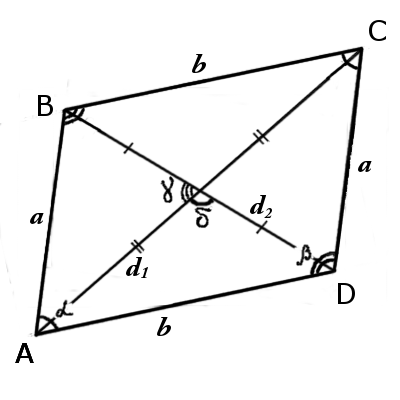 | 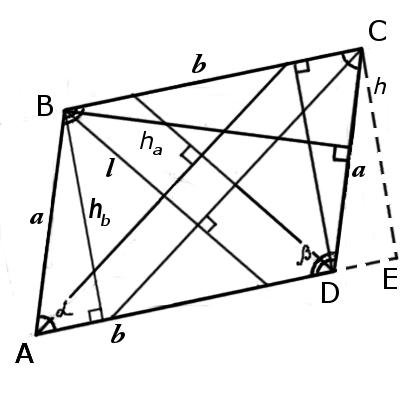 |
| Рис.1 | Рис.2 |
Признаки параллелограмма
AB||CD, AB = CD (или BC||AD, BC = AD)
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Основные свойства параллелограмма
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d 1 |
| 2 | |
| BO = DO = | d 2 |
| 2 |
AC 2 + BD 2 = 2AB 2 + 2BC 2
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
2. Формула сторон параллелограмма через диагонали и другую сторону:
3. Формула сторон параллелограмма через высоту и синус угла:
| a = | h b |
| sin α |
| b = | h a |
| sin α |
4. Формула сторон параллелограмма через площадь и высоту:
| a = | S |
| ha |
| b = | S |
| hb |
Диагонали параллелограмма
Формулы определения длины диагонали параллелограмма:
d 2 = √ a 2 + b 2 + 2 ab·cosβ
d 1 = √ a 2 + b 2 + 2 ab·cosα
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d 1 = | 2S | = | 2S |
| d 2· sinγ | d 2· sinδ |
| d 2 = | 2S | = | 2S |
| d 1· sinγ | d 1· sinδ |
Периметр параллелограмма
Формулы определения длины периметра параллелограмма:
P = 2 a + 2 b = 2( a + b )
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
| P = | 2( b + | h b | ) |
| sin α |
| P = | 2( a + | h a | ) |
| sin α |
Площадь параллелограмма
Формулы определения площади параллелограмма:
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
| S = | 1 | d 1 d 2 sin γ |
| 2 |
| S = | 1 | d 1 d 2 sin δ |
| 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Параллелограмм: свойства и признаки
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Параллелограмм. Свойства и признаки параллелограмма
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
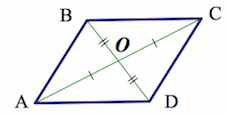
6. Точка пересечения диагоналей является центром симметрии параллелограмма
7. Диагонали параллелограмма и стороны
связаны следующим соотношением:
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны:
2. Противоположные углы попарно равны:
3. Диагонали пересекаются и в точке пересечения делятся пополам
4. Противоположные стороны равны и параллельны:
5.
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:
 Формулы площади параллелограмма смотрите здесь.
Формулы площади параллелограмма смотрите здесь.Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.
Диагонали параллелограмма?
Равны ли диагонали параллелограмма? Диагонали a параллелограмм равны. Противоположные стороны и противоположные углы параллелограмма равны. И эти противоположные стороны и углы составляют два конгруэнтных треугольника, причем две диагонали являются сторонами этих двух конгруэнтных треугольников.
Кроме того, каковы 5 свойств параллелограмма?
Параллелограмм обладает следующими свойствами:
При этом, какая форма представляет собой параллелограмм?
Параллелограмм: Четырехугольник с 2 парами параллельных сторон.
Также узнать, у какого параллелограмма одинаковые диагонали? Прямоугольник является параллелограммом, поэтому его противоположные стороны равны. Диагонали прямоугольника равны и делят друг друга пополам.
Какова длина диагонали параллелограмма?
Какая формула диагонали параллелограмма?
Часто задаваемые вопросы о диагонали формулы параллелограмма
Что не является свойствами параллелограмма?
Если же линия индикатора четыре стороны не соединяются в своих конечных точках, у вас нет замкнутой формы; нет параллелограмма! Если одна сторона длиннее противоположной, у вас нет параллельных сторон; нет параллелограмма! Если только один набор противоположных сторон конгруэнтен, у вас нет параллелограмма, у вас есть трапеция.
Каковы три свойства параллелограмма?
Объяснение свойств параллелограммов
Почему его называют параллелограммом?
Здесь все стороны равны, а все углы прямые. Диагонали AC и BD равны. Термин «параллелограмм» происходит от среднефранцузского «параллелограмма», позднелатинского «параллелограмм» и греческого «параллелограммон», что означает «ограничен параллельными линиями ».
Какая форма не параллелограмм?
Обычный четырехугольник без равных сторон не является параллелограммом. А воздушный змей не имеет параллельных линий вообще. У трапеции и равнобедренной трапеции одна пара противоположных сторон параллельна. Вогнутый четырехугольник или наконечник стрелы не имеет параллельных сторон.
Равна ли диагональ ромба?
Диагонали ромбы пересекаются под равными углами, а диагонали прямоугольника равны по длине.
Какая большая и малая диагонали параллелограмма?
Диагональ, проходящая через больший угол, называется малой диагональю. из-за небольшого размера. Диагональ, проходящая через Меньший угол, называется большой диагональю из-за ее размера.
Что такое диагональная формула?
Какова длина большей диагонали в параллелограмме быстрого?
Ответ: Длина самой длинной диагонали параллелограмма равна 24.86.
По какой формуле найти диагональ параллелограмма?
Часто задаваемые вопросы о диагонали формулы параллелограмма
Как найти большую диагональ параллелограмма?
Что такое диагональ?
Какая форма у параллелограмма?
Параллелограмм: Четырехугольник с 2 парами параллельных сторон.
Какой формы четырехугольник, но не параллелограмм?
Почему диагонали параллелограмма не равны?
Диагонали параллелограмма не равны. Если бы они были, фигура будет прямоугольником. А если бы стороны тоже были равны, фигура была бы квадратом! Поскольку к параллелограмму примыкают острые и тупые углы, диагонали разбивают фигуру на 2 пары равных треугольников.
Что такое примеры параллелограмма?
В геометрии четырехугольник называется параллелограммом. У параллелограмма противоположные стороны параллельны и равны по длине. Несколько примеров параллелограмма: ромб, прямоугольник и квадрат.
У параллелограмма четыре прямых угла?
Прямоугольник параллелограмм с четырьмя прямыми углами, поэтому все прямоугольники также параллелограммы и четырехугольники. С другой стороны, не все четырехугольники и параллелограммы являются прямоугольниками. Прямоугольник обладает всеми свойствами параллелограмма, а также следующими: диагонали совпадают.
Параллелограмм — признаки и свойства
Клод Бернард однажды сказал:
«Думать, что всё знаешь, останавливает тебя от того, чтобы учиться новому»
Давай узнаем что-то новое сегодня, разбирая, казалось бы, такую простую тему!
Статья поможет тебе окончательно разобраться с самыми «популярными» параллелограммами, а наши вебинары дадут тебе необходимую практику.
И на ЕГЭ ты сможешь решить любую задачу на эту тему!
Параллелограмм — коротко о главном
Параллелограмм – четырехугольник, противоположные стороны которого попарно параллельны.
Свойства параллелограмма:
Прямоугольник – четырехугольник, все углы которого прямые: \( \displaystyle \angle A=\angle B=\angle C=\angle D=90<>^\circ \).
Свойства прямоугольника:
Ромб – четырехугольник, все стороны которого равны между собой: \( \displaystyle AB=BC=CD=DA\).
Свойства ромба:
Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые: \( \displaystyle AB=BC=CD=DA\); \( \displaystyle \angle A=\angle B=\angle C=\angle D=90<>^\circ \).
Свойства квадрата:
\( \displaystyle ABCD\) – ромб