Что такое диагональ пирамиды
Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида
Что такое пирамида в общем случае?
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.
Правильная четырехугольная пирамида
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.
Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.
Египетские пирамиды в Гизе являются правильными четырехугольными.
Далее приведем формулы, позволяющие определить все характеристики этой фигуры.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):
Очевидно, что боковое ребро b всегда больше апофемы ab.
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.
Площадь и объем фигуры
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:
Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:
S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.
Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
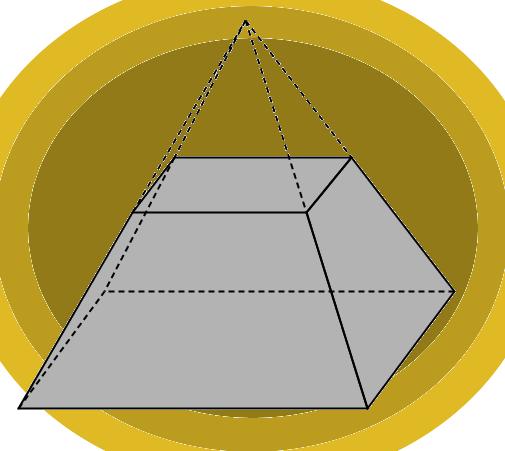
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (So1 + So2 + √(So1 × So2))
Пирамида
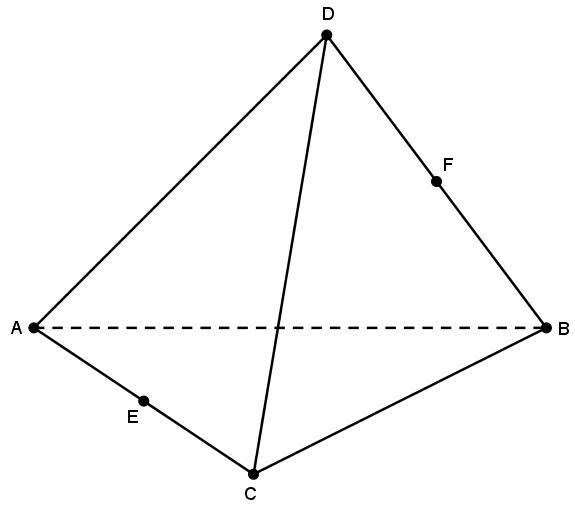
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
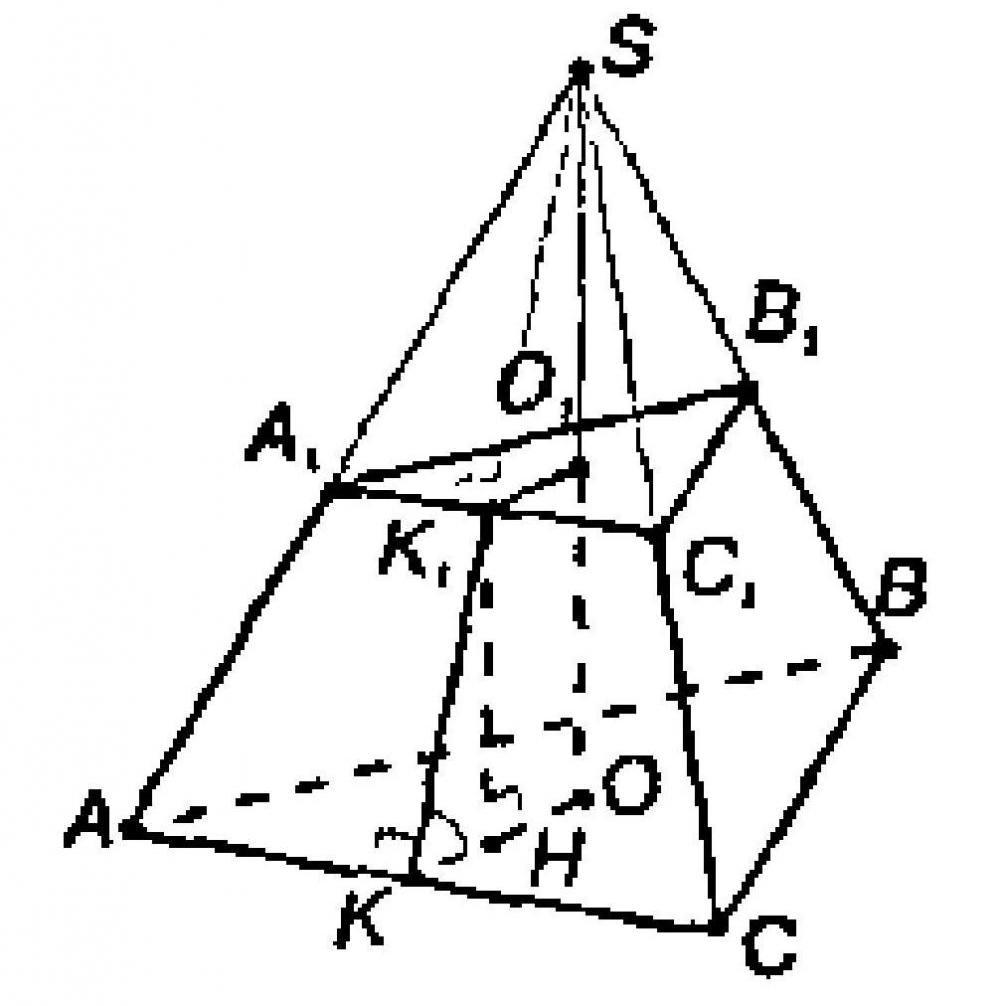
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Виды пирамид
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Что такое пирамида: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение пирамиды
Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.
Примечание: пирамида – это частный случай конуса.
Элементы пирамиды
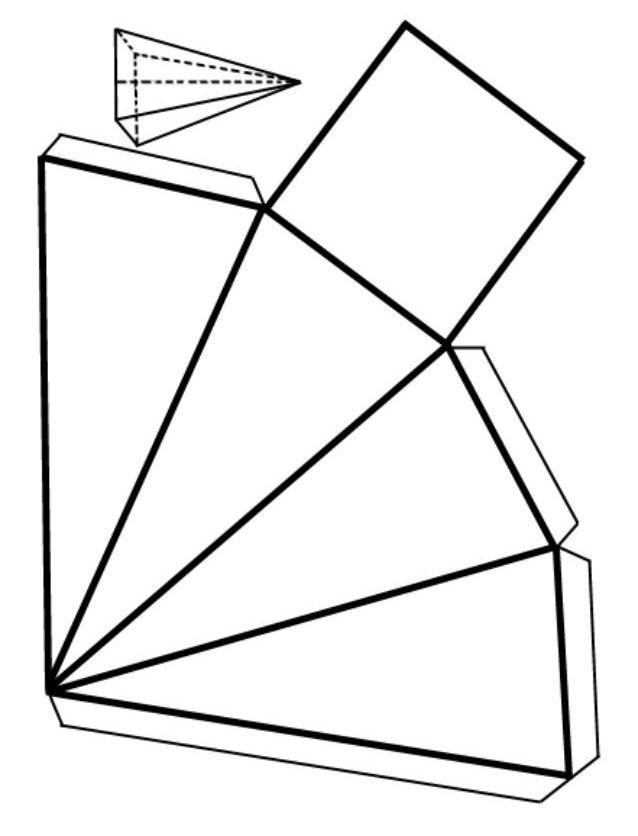
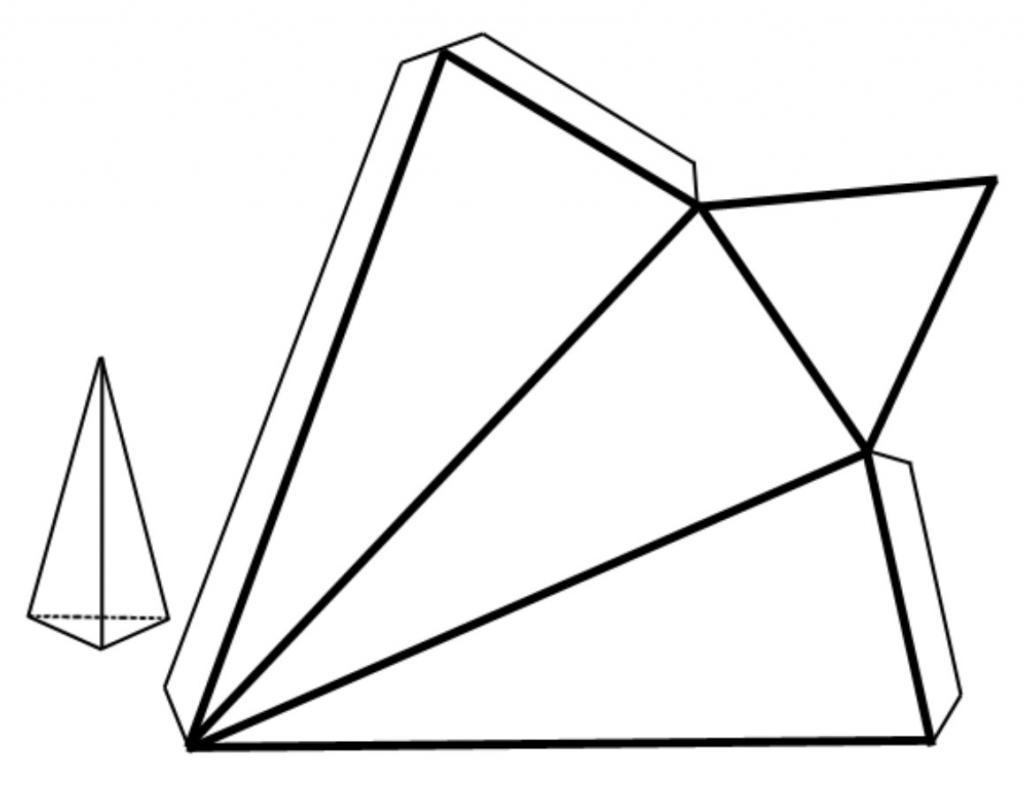
Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.
Примечание: свойства пирамиды представлены в отдельной публикации.
Виды сечения пирамиды
1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):
2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.
Примечание: Существуют и другие виды сечения, но они не так распространены.
Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.
Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
Геометрические фигуры. Пирамида.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани являются треугольниками, которые имеют общую вершину. Пирамида – это частный случай конуса.
Элементы пирамиды.
Свойства пирамиды.
1. Когда все боковые ребра имеют одинаковую величину, тогда:
2. Когда боковые грани имеют угол наклона к плоскости основания одной величины, тогда:
3. Около пирамиды можно описать сферу в том случае, если в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы станет точка пересечения плоскостей, которые проходят через середины ребер пирамиды перпендикулярно им. Из этой теоремы делаем вывод, что как около всякой треугольной, так и около всякой правильной пирамиды можно описать сферу.
4. В пирамиду можно вписать сферу в том случае, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в 1-ной точке (необходимое и достаточное условие). Эта точка станет центром сферы.
5. Конус будет вписанным в пирамиду, когда вершины их совпадут, а основание конуса будет вписанным в основание пирамиды. При этом вписать конус в пирамиду можно лишь в том случае, если апофемы пирамиды имеют равные величины (необходимое и достаточное условие).
6. Конус будет описанным около пирамиды, если их вершины совпадут, а основание конуса будет описано около основания пирамиды. При этом описать конус около пирамиды можно лишь в том случае, если все боковые ребра пирамиды имеют одинаковые величины (необходимое и достаточное условие). Высоты у этих конусов и пирамид одинаковы.
7. Цилиндр будет вписанным в пирамиду, если 1-но его основание совпадет с окружностью, которая вписана в сечение пирамиды плоскостью, параллельной основанию, а второе основание будет принадлежать основанию пирамиды.
8. Цилиндр будет описанным около пирамиды, когда вершина пирамиды будет принадлежать его одному основанию, а второе основание цилиндра будет описано около основания пирамиды. При этом описать цилиндр около пирамиды можно лишь в том случае, если основанием пирамиды служит вписанный многоугольник (необходимое и достаточное условие).
Виды пирамид.
По количеству углов основания пирамиды делят на треугольные, четырехугольные и так далее.
Пирамида будет треугольной, четырехугольной, и так далее, когда основанием пирамиды будет треугольник, четырехугольник и так далее. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и так далее.