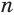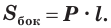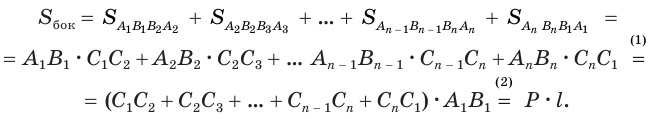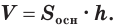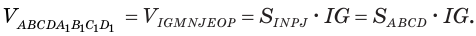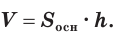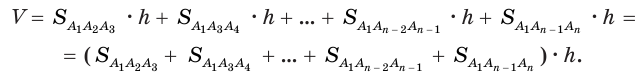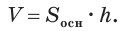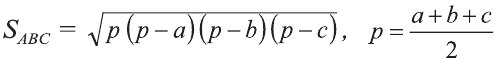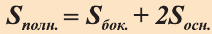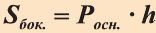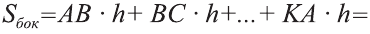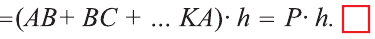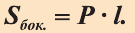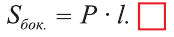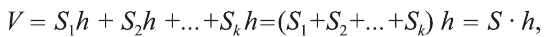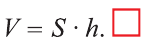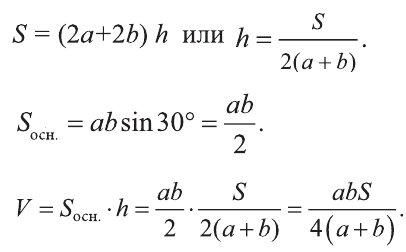Что такое диагональ призмы что такое диагональное сечение
Призма. Виды призмы
Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.
Мы же поведем подробный разговор.
Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и
, лежащих в параллельных плоскостях, и
параллелограммов
.
Боковые грани – все грани, кроме оснований ( являются параллелограммами ).
Боковые ребра – общие стороны боковых граней ( параллельны между собой и равны ).
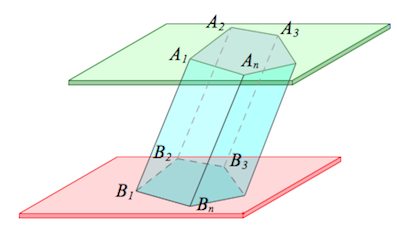
Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.
Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.
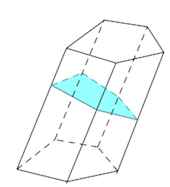
Диагональное сечение –пересечение призмы и диагональной плоскости.
Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
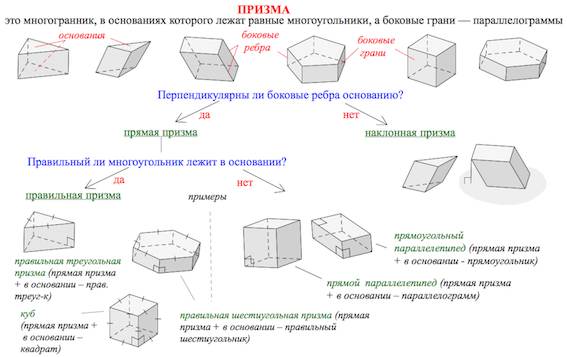
Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).
Среди прямых призм выделяют правильные.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).
Параллелепипед – это призма, основаниями которой являются параллелограммы.
Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.
Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Частный случай прямоугольного параллелепипеда – куб.
Куб – прямоугольный параллелепипед, все грани которого – квадраты.
Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике.

Чтобы не потерять страничку, вы можете сохранить ее у себя:
Содержание:
Ранее вы уже знакомились с призмой, т. е. многогранником, две грани которого — равные
Что такое призма
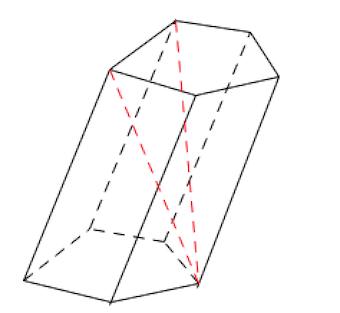
Равные грани-многоугольники призмы лежат в параллельных плоскостях и называются основаниями призмы, а остальные грани-параллелограммы — боковыми гранями. Ребра боковых граней, не принадлежащие основаниям, называют боковыми ребрами. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называют диагональю призмы (рис. 1). Плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани, называется диагональной плоскостью, а сечение призмы диагональной плоскостью — диагональным сечением. На рисунке 2 показаны два диагональных сечения призмы.
Призмы разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Призма, изображенная на рисунке 1, — шестиугольная, а на рисунке 2, — девятиугольная.
Отличают прямые и наклонные призмы в зависимости от того, перпендикулярны или не перпендикулярны боковые ребра призмы ее основаниям. Обычно при изображении прямой призмы ее боковые ребра проводят вертикально.
Прямая призма, основаниями которой являются правильные многоугольники, называется правильной призмой. В прямой призме все боковые грани — прямоугольники, а в правильной — равные прямоугольники.
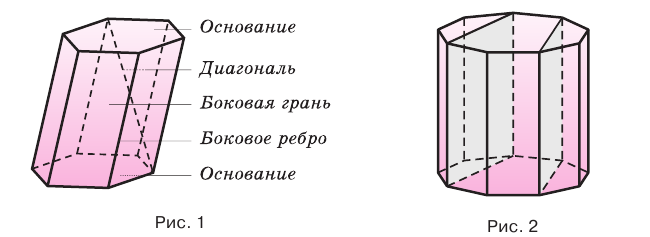
Перпендикуляр, проведенный из какой-либо точки одного основания призмы к плоскости другого основания, называется высотой призмы. На рисунке 3 показаны две высоты 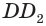
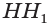
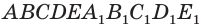
Боковые грани составляют боковую поверхность призмы, а боковые грани вместе с основаниями — полную поверхность призмы.
Теорема 1.
Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра:
Доказательство:
Пусть имеется 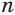
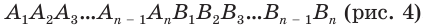
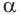
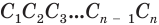
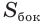
При переходе (1) мы учли, что все боковые ребра призмы равны друг другу, при переходе (2) — то, что сумма 
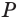
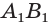
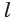
Следствие 1.
Площадь боковой поверхности прямой призмы равна произведению периметра ее основания и высоты.
Действительно, перпендикулярное сечение прямой призмы равно ее основанию, а боковое ребро является высотой.
Частным видом призмы является параллелепипед, т. е. призма, основанием которой является параллелограмм. Параллелепипед, как и призма, может быть прямым или наклонным. Прямой параллелепипед, основаниями которого являются прямоугольники, называется прямоугольным параллелепипедом. Прямоугольный параллелепипед, у которого три ребра, выходящие из одной вершины, равны друг другу, называется кубом.
У параллелепипеда все грани — параллелограммы, из которых у прямого параллелепипеда прямоугольниками являются боковые грани, а у прямоугольного параллелепипеда — все грани.
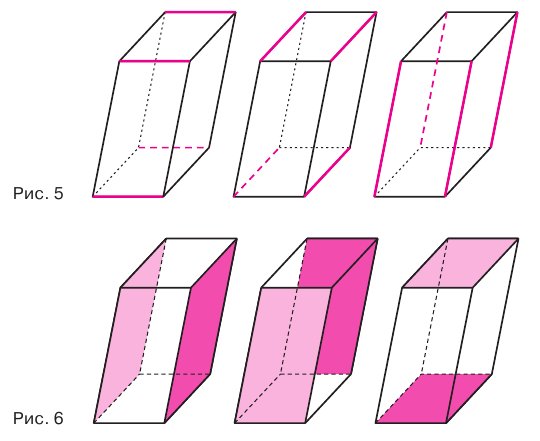
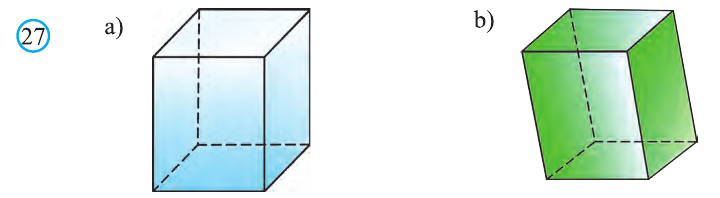
12 ребер параллелепипеда разделяются на три четверки равных ребер (рис. 5), его 6 граней — на три пары равных граней (рис. 6), а 4 диагонали пересекаются в одной точке, являющейся центром симметрии параллелепипеда (рис. 7).
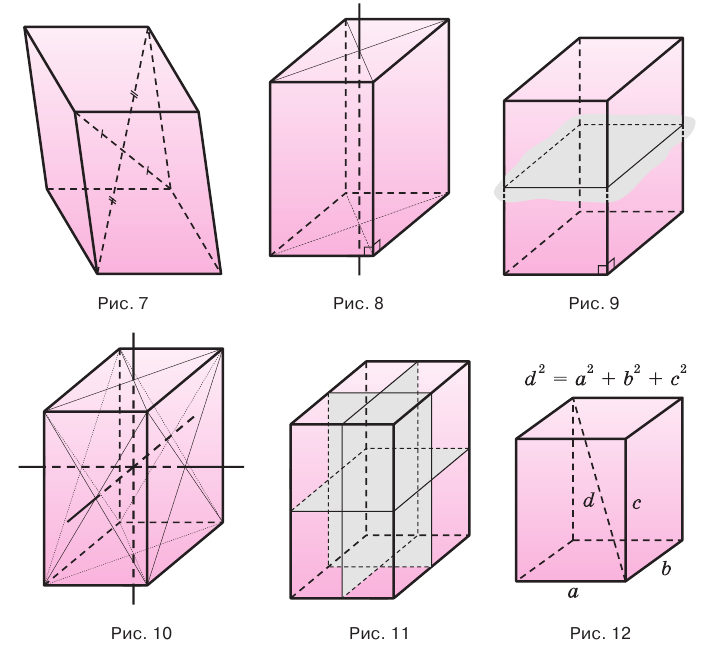
Прямой параллелепипед еще имеет ось симметрии (рис. 8) и плоскость симметрии (рис. 9). Прямоугольный параллелепипед имеет три оси симметрии (рис. 10) и три плоскости симметрии (рис. 11).
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, называют измерениями прямоугольного параллелепипеда. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (рис. 12), и все его диагонали равны друг другу.
Важной характеристикой плоской фигуры является ее площадь. Подобной характеристикой тела является его объем. Будем считать, что изучаемые нами тела имеют объем.
За единицу объема принимают объем куба с ребром 1. На практике пользуются разными единицами объема: как метрическими — кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр, кубический километр, так и неметрическими — галлон, барель, бушель, кварта.
Для объема тела выполняются его основные свойства:
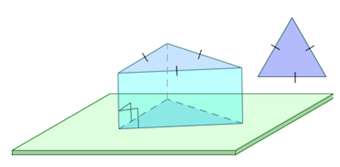
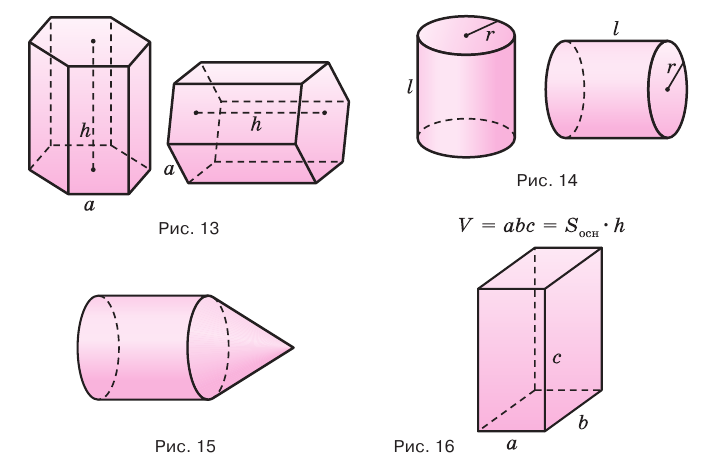
При этом равными фигурами называют фигуры, которые преобразуются друг в друга определенным движением. Например, равными являются две шестиугольные правильные призмы, у которых соответственно равны стороны оснований и высоты (рис. 13), или два цилиндра с соответственно равными радиусами оснований и образующими (рис. 14). Тело, изображенное на рисунке 15, можно разделить на цилиндр и конус, и его объем равен сумме объемов этих цилиндра и конуса.
Два тела с равными объемами называют равновеликими телами. Равные тела являются равновеликими, но не наоборот.
Вы знаете, что объем 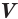
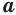
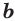
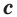
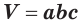
Учитывая, что в формуле 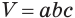
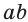
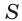
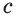
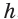
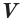

Теорема 2.
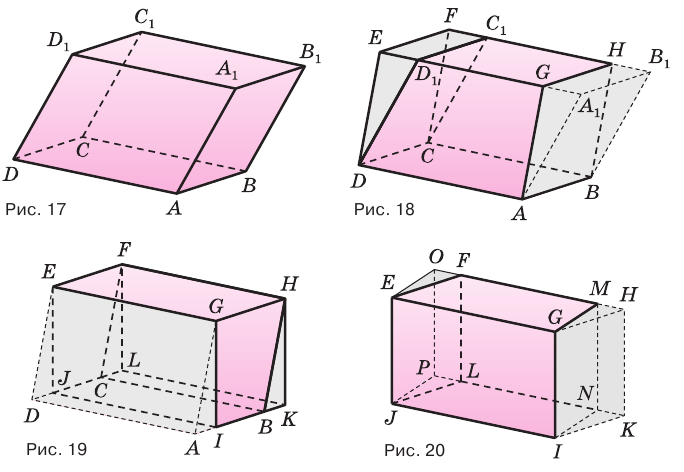
Объем произвольного параллелепипеда равен произведению площади его основания и высоты:
Доказательство:
Пусть имеется произвольный параллелепипед 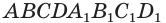
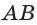
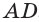
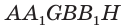
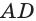
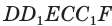
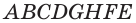
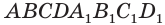
У параллелепипеда 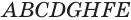
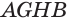

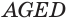
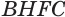
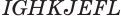
Наконец, применив еще раз такое преобразование к граням 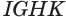

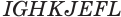
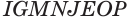
Множитель 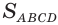
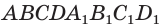
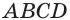
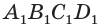
Теорема 3.
Объем призмы равен произведению площади ее основания и высоты:
Доказательство:
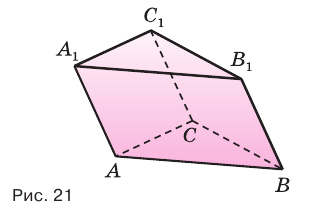
Рассмотрим сначала треугольную призму 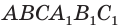
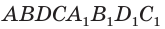
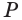
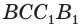
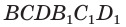
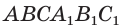
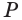
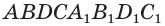
Объем параллелепипеда 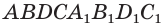
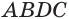
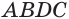
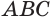
Отсюда следует, что объем призмы 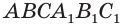
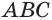
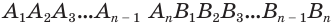
Учитывая, что сумма в скобках выражает площадь S основания данной призмы, получим:
Следствие 2.
Объем прямой призмы равен произведению площади ее основания и бокового ребра.
Призма и её сечения
С призмой вы уже знакомы. Несмотря на это, мы напомним определение призмы и её свойства.
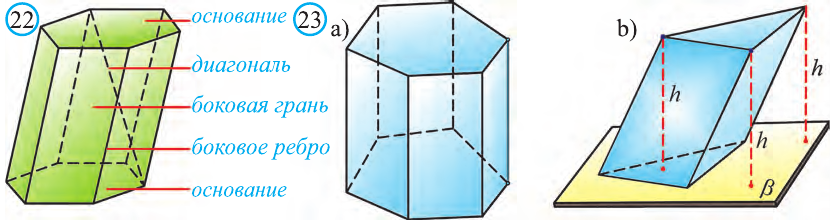
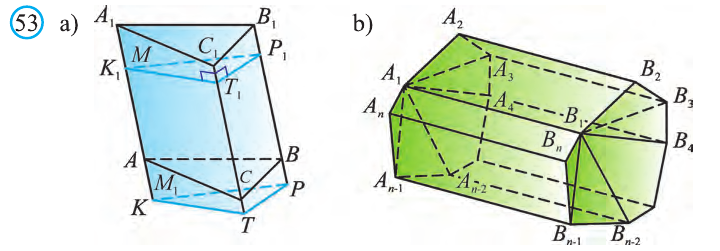
Если основания прямой призмы являются правильными многоугольниками, то её называют правильной (рис. 24). Боковые грани правильной призмы это равные между собой прямоугольники.
Перпендикуляр, опущенный из некоторой точки одного основания к другому, называют его перпендикуляром (рис. 23.b).
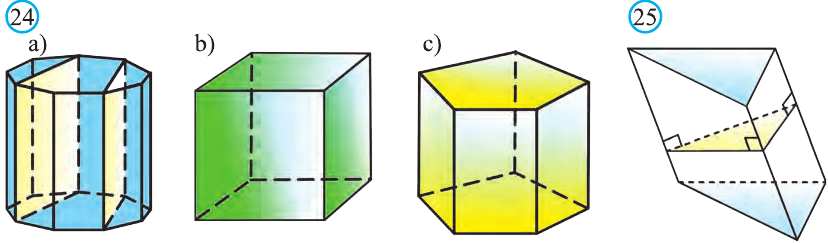
Сечение призмы, проходящее через соответствующие диагонали его оснований, называют диагональным сечением (рис. 24.а) и их число равно числу диагоналей одного из оснований.
Перпендикулярным сечением призмы называют сечение перпендикулярное всем его боковым рёбрам (рис. 25). так как 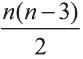
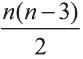
В каждом диагональном сечении призмы можно провести две диагонали. Следовательно, n-угольная призма имеет 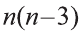
Пример:
В наклонной треугольной призме расстояния между боковыми ребрами соответственно равны 7 см, 15 см и 20 см. Найдите расстояние между большей боковой гранью и противолежащим боковым ребром.
Решение:
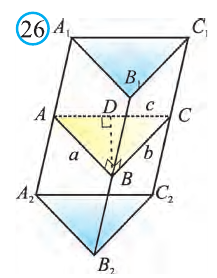
Известно, что расстояние между параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки одной прямой на другую. Тогда длины сторон перпендикулярного сечения ABC (рис. 26). Наибольшая грань призмы проходит через наибольшую сторону АС= 20 см этого сечения. Расстояние от рёбра призмы В2В1 до плоскости грани 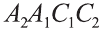
Тогда по формуле Герона получаем:
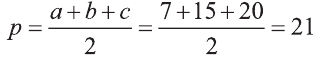
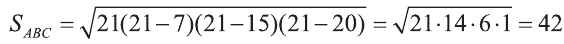
С другой стороны, 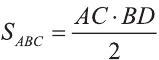
Отсюда 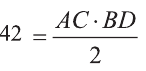
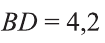
Ответ: 4,2 см.
Параллелепипед и куб
Призма, основаниями которой являются параллелограммы, называют параллелепипедом (рис. 27). Параллелепипеды также как и призмы могут быть прямыми (рис. 27.а) и наклонными (рис. 27.b).
Грани параллелепипеда, не имеющие общую вершину, называют противоположными гранями.
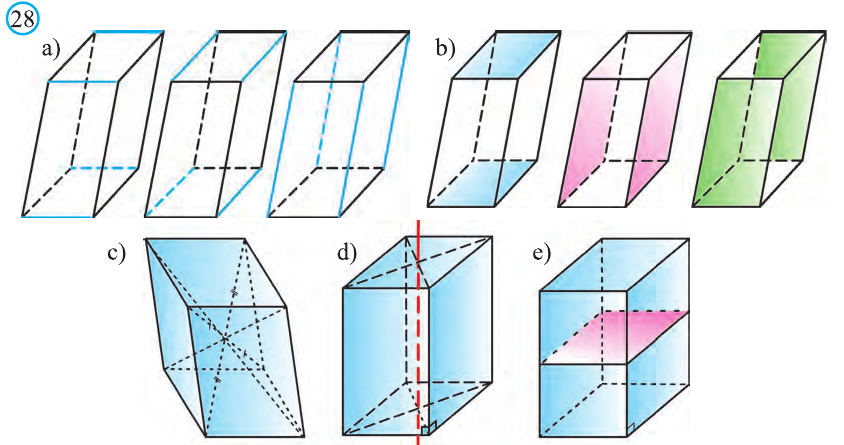
Прямой параллелепипед, основания которого являются прямоугольники, называют прямоугольным параллелепипедом (рис. 29). Очевидно, что все грани прямоугольного параллелепипеда являются прямоугольниками.
Прямоугольный параллелепипед имеет три оси симметрии (рис. 30) и три плоскости симметрии (рис. 31).
Длины трех рёбер, исходящих из одной вершины прямоугольного параллелепипеда называют его измерениями.
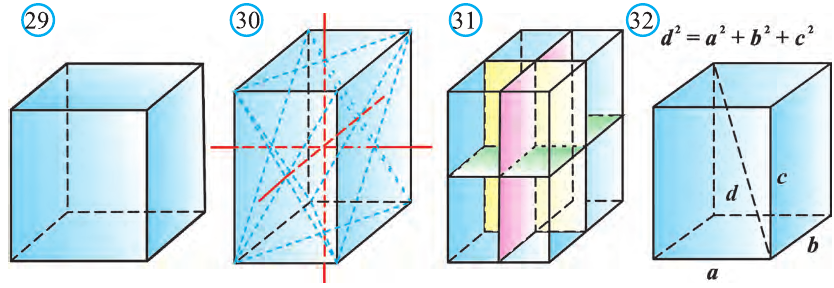
Свойство: В прямоугольном параллелепипеде квадрат любой диагонали d равен сумме квадратов его измерений: а, b и с (рис.32):
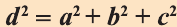
Прямоугольный параллелепипед, все измерения которого равны, называют кубом. Очевидно, что все грани куба являются равными квадратами. Куб имеет один центр симметрии, 9 осей симметрии и 9 плоскостей симметрии.
Выше были перечислены свойства призмы. Некоторые из них были показаны в 10 классе. Доказательства остальных свойств проще, поэтому их доказательства вы можете провести самостоятельно.
Площади боковой и полной поверхности призмы
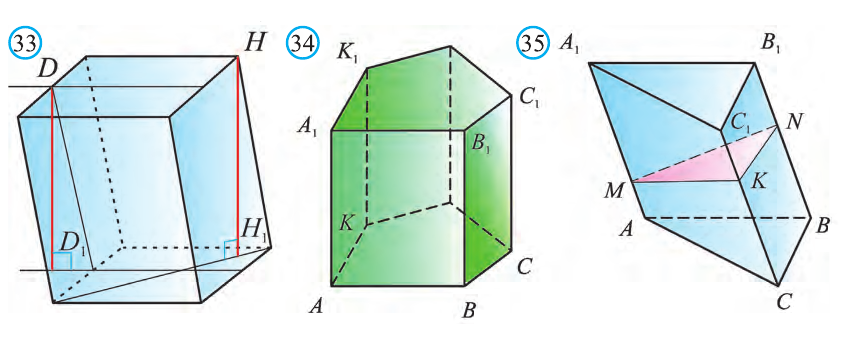
На рисунке 33 проведены высоты НН1 DD1 призмы
АВСDЕ—А1В1С1D1Е1. Очевидно, что высоты правильной призмы будут равны её боковому рёбру.
Боковая поверхность призмы (точнее, площадь боковой поверхности)равна сумме боковых поверхностей ее граней, а полная поверхнасть равна сумме боковой поверхности и площадей двух ее оснований.
Теорема. Боковая поверхность прямой призмы равна произведению периметра ее основания на высоту:
Доказательство. Пусть высота данной прямой призмы равна 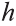
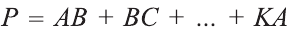
Тогда
Теорема. Боковая поверхность произвольной призмы равна произведению периметра перпендикулярного сечения призмы на ее боковое ребро:
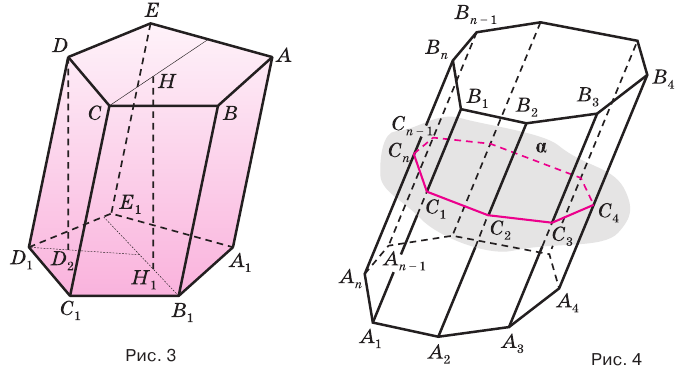
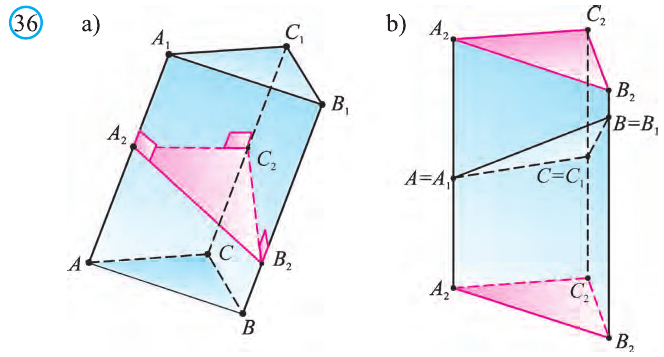
Доказательство. Пусть периметр перпендикулярного сечения призмы равен Р (рис. 35). Сечение делит призму на две части (рис. 36.а). Совершим параллельный перенос одной из этих частей так, чтобы основания нашей призмы совпали. В результате мы получим новую прямую призму (рис. 36.b). Очевидно, что, боковая поверхность этой призмы равна боковой поверхности данной. Её основанием является перпендикулярное сечение, а боковое ребро равно 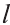
Тогда по доказанной выше теореме:
Объем призмы
Одним из свойств, характеризующих геометрические тела в пространстве, является понятие объема. Каждый предмет (тело) занимает некоторую часть пространства. Например, кирпич по сравнению со спичечным коробком занимает большую часть пространства. Для сравнения этих частей между собой вводится понятие объёма.
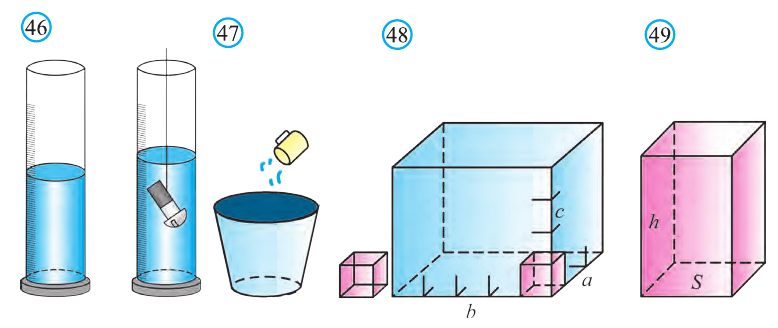
Объёмы тел измеряют различными способами или вычисляют. Например, объёмы маленьких предметов можно измерить с помощью сосудов (мензурки) с мелкими делениями (шкалами) (рис. 46). А объём ведра можно измерить с помощью сосуда, имеющего единичный объём, наполнив его водой (рис. 47). Но таким способом мы не можем измерить объёмы всех тел. В таких случаях объём вычисляют различными способами. Ниже рассмотрим их без доказательств.
Объём параллелепипеда
Теорема. Объём прямоугольного параллелепипеда равен произведению трех его измерeний (рис.48): 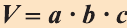
Следствие. Объём прямоугольного параллелепипеда равен произведению площади его основания на высоту (рис. 49): 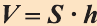
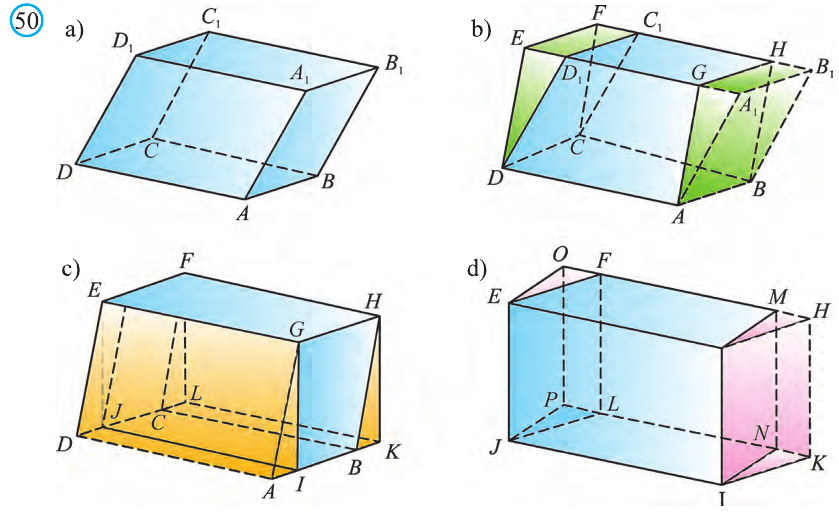
Теорема. Объём произвольного параллелепипеда равен произведению площади его основания на высоту (рис. 50): 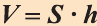
Это свойство вытекает из вышеупомянутого следствия. На рисунке 50 показано как данный параллелепипед преобразовать в прямоугольный параллелепипед. Воспользовавшись этим самостоятельно обоснуйте свойство.
Нахождение объёма призмы
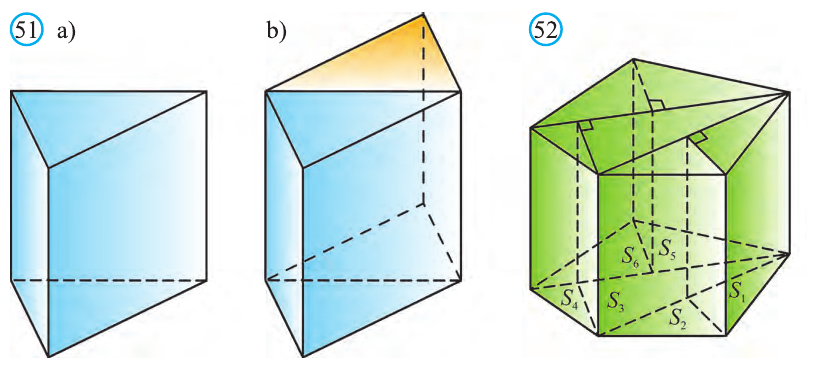
Теорема. Объём прямой призмы равен произведению площади его основания на высоту (рис. 51): 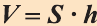
Если объём данной призмы, площадь её основания и высота V, S и h, то объём полученного прямоугольного параллелепипеда, площадь его основания и высота будут соответственно равны 2V, 2S и h.
Следовательно 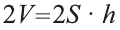
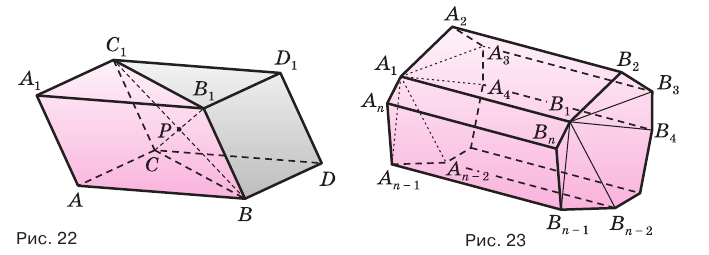
Объём данной призмы равен сумме объёмов составляющих её треугольных призм:
или
Теорема. Объём произвольной призмы равен произведению площади его основания на высоту:
По рисунку 5.3 докажите эту теорему самостоятельно, сначала для треугольной призмы (рис. 5.3.а), затем для любой призмы (рис. 5.3.b).
Пример:
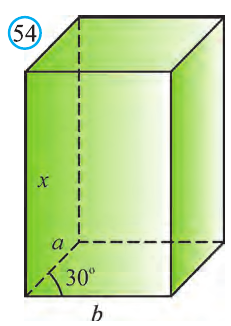
Стороны основания прямого параллелепипеда равны а и b, а угол между ними 30°. Найдите его объём, если площадь его боковой поверхности равна S.
Решение:
Обозначим высоту параллелепипеда h(рис. 54).
Тогда по условию задачи:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.