Что такое диаграмма растяжения

§ 9.3. Механические свойства твердых тел. Диаграмма растяжения

Напряжение

В любом сечении деформируемого тела действуют силы упругости, препятствующие разрыву тела на части (рис. 9.15). Деформированное тело находится в напряженном состоянии, которое характеризуется особой величиной, называемой механическим напряжением или короче — напряжением.

Напряжение — величина, равная отношению модуля силы упругости к площади поперечного сечения(1) тела:

где σ — напряжение, F_ynp — модуль силы упругости и S — площадь поперечного сечения.

В СИ за единицу напряжения принимается паскаль (Па):

Заметим, что в формуле (9.3.1) иногда удобно модуль силы упругости заменить на модуль F внешней деформирующей силы, уравновешивающей силу упругости.

Диаграмма растяжения

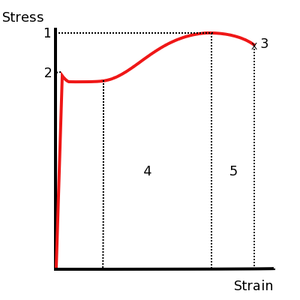
Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств (например, с помощью гидравлического пресса) подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения с от относительного удлинения е. Этот график называют диаграммой растяжения (рис. 9.16).

Закон Гука

Многочисленные опыты показывают, что при малых деформациях напряжение а прямо пропорционально относительному удлинению ε (участок ОА диаграммы). Эта зависимость называется законом Гука. Его можно записать так:

Относительное удлинение в формуле (9.3.2) взято по модулю, так как закон Гука справедлив как для деформации растяжения, так и для деформации сжатия, когда ε

Закон Гука для деформации сдвига

Опыт показывает, что касательное напряжение х при малых деформациях прямо пропорционально углу сдвига а. Это и есть закон Гука для деформации сдвига. Он записывается так:

Коэффициент у называется модулем сдвига. Он численно равен касательному напряжению при угле сдвига в 1 рад. Очевидно, что для абсолютного большинства реальных материалов такое напряжение нельзя приложить к реальным телам, не разрушая их.

В СИ единицей модуля сдвига является 1 Па/рад.

Наиболее полную информацию об упругих свойствах материалов дает диаграмма растяжения, получаемая экспериментально. При малых деформациях напряжение в твердом теле прямо пропорционально относительной деформации (закон Гуна).

(1) Сечение тела производится плоскостью, перпендикулярной направлению силы упругости. При этом предполагается, что деформация тела во всех участках сечения одинакова.

Источник

Статическое растяжение

Статическое растяжение — одно из наиболее распространённых видов испытаний для определения механических свойств материалов.

Содержание

Основные характеристики, определяемые при испытании

При статическом растяжении, как правило, определяются следующие характеристики материала.

Основные типы материалов

Принято разделять пластичные и хрупкие материалы. Основное отличие состоит в том, что первые деформируются в процессе испытаний с образованием пластических деформаций, а вторые практически без них вплоть до своего разрушения. За критерий для условной классификации материалов можно принять относительное остаточное удлинение δ = (l_к − l₀)/l₀, где l₀ и l_к — начальная и конечная длина рабочей части образца), обычно вычисляемое в процентах. В соответствии с величиной остаточного удлинения материалы можно разделить на:

Для испытаний на статическое растяжение используют образцы как с круглым, так и с прямоугольным сечением. Предъявляются повышенные требования к изготовлению образцов, как с точки зрения геометрии, так и с точки зрения обработки резанием. Требуется высокая однородность диаметра образца по его длине, соосность и высокое качество поверхности (малая шероховатость, отсутствие царапин и надрезов). При изготовлении образцов следует избегать перегрева материала и изменений его микроструктуры.

Образцы круглого сечения, как правило, имеют рабочую длину, равную четырём или пяти диаметрам — т. н. короткие образцы или десяти диаметрам — т. н. нормальные образцы. Перед началом испытания замеряется диаметр образца (обычно 6, 10 или 20 мм) для вычисления напряжения σ и для расчёта относительного остаточного сужения после разрушения образца. В случае использования экстензометра, длина рабочей части образца не замеряется, а деформация ε и относительное удлинение при разрушении регистрируются автоматически с помощью компьютера или измеряются по диаграмме σ — ε. При отсутствии экстензометра (не рекомендуется стандартом), отмечается рабочая длина образца, деформация ε рассчитывается по перемещениям конца образца (захвата), а относительное удлинение при разрушении рассчитывается путём замера разрушенного образца.

Диаграмма растяжения пластичного материала

Обычно диаграмма растяжения является зависимостью приложенной нагрузки P от абсолютного удлинения Δl. Современные машины для механических испытаний позволяют записывать диаграмму в величинах напряжения σ (σ = P/A₀, где A₀ — исходная площадь поперечного сечения) и линейной деформации ε (ε = Δl/l₀ ). Такая диаграмма носит название диаграммы условных напряжений, так как при этом не учитывается изменение площади поперечного сечения образца в процессе испытания.

Начальный участок является линейным (т. н. участок упругой деформации). На нём действует закон Гука:

Затем начинается область пластической деформации. Эта деформация остаётся и после снятия приложенной нагрузки. Переход в пластическую область обнаруживается не только по проявлению остаточных деформаций, но и по уменьшению наклона кривой с увеличением степени деформации. Данный участок диаграммы обычно называют площадкой (зоной) общей текучести, так как пластические деформации образуются по всей рабочей длине образца. С целью изучения и точного анализа диаграммы деформации, современные испытательные машины оснащены компьютеризированной записью результатов.

По наклону начального участка диаграммы рассчитывается модуль Юнга. Для малоуглеродистой стали наблюдается т. н. «зуб текучести» и затем площадка предела текучести. Явление «зуба» текучести связано с дислокационным механизмом деформации. На начальном участке плотность дислокаций является недостаточной для обеспечения более высокой степени деформации. После достижения точки верхнего предела текучести начинается интенсивное образование новых дислокаций, что приводит к падению напряжения. Дальнейшая деформация при пределе текучести происходит без роста напряжения . Зависимость предела текучести, от размера зерна, d, выражена соотношением Холла-Петча:

После достижения конца площадки текучести (деформация порядка 2 — 2,5 %) начинается деформационное упрочнение (участок упрочнения), видимое на диаграмме, как рост напряжения с ростом деформации. В этой области до достижения максимальной нагрузки (напряжения (σ_В) макродеформация остаётся равномерной по длине испытуемого образца. После достижения точки предела прочности начинает образовываться т. н. «шейка» — область сосредоточенной деформации. Расположение «шейки» зависит от однородности геометрических размеров образца и качества его поверхности. Как правило, «шейка» и, в конечном счёте, место разрушения расположено в наиболее слабом сечении. Кроме того, важное значение имеет одноосность напряжённого состояния (отсутствие перекосов образца в испытательной машине). Для пластичных материалов при испытании на статическое растяжение одноосное напряжённое состояние сохраняется лишь до образования т. н. «шейки» (до достижения максимальной нагрузки и начала сосредоточенной деформации).

Вид диаграммы деформации, приведённый на рис. 1 является типичным для О.Ц.К. материалов с низкой исходной плотностью дислокаций.

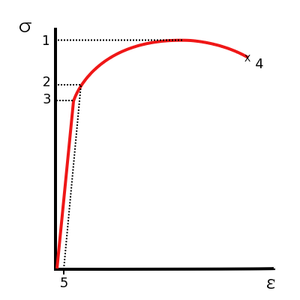
Для многих материалов, например, с Г. Ц. К. кристаллической решёткой, а также для материалов с высокой исходной плотностью дефектов, диаграмма имеет вид, показанный на рис. 2. Основное отличие — отсутствие явно выраженного предела текучести. В качестве предела текучести выбирается значение напряжения при остаточной деформации 0,2 % (σ_0.2).

После достижения максимума нагрузки происходит падение нагрузки (и, соответственно, напряжения σ) за счёт локального уменьшения площади поперечного сечения образца. Соответствующий (последний) участок диаграммы называют зоной местной текучести, так как пластические деформации продолжают интенсивно развиваться только в области шейки.

Иногда используется диаграмма истинных напряжений, S — e (истинное напряжение S = P/A, где A — текущая площадь поперечного сечения образца; истинная деформация e = Δl/l, где l — текущая длина образца). В этом случае, после достижения максимальной нагрузки не происходит падения напряжения, истинное напряжение растёт за счёт локального уменьшения сечения в «шейке» образца. Поэтому различие между диаграммами истинных и условных напряжений наблюдается только после предела прочности — до точки 1 они практически совпадают друг с другом.

Образцы из пластичного материала разрушаются по поперечному сечению с уменьшением диаметра в месте разрыва из-за образования «шейки».

Диаграмма растяжения хрупкого материала

Диаграмма растяжения и диаграмма условных напряжений хрупких материалов по виду напоминает диаграмму, показанную на рис. 2 за тем исключением, что не наблюдается снижения нагрузки (напряжения) вплоть до точки разрушения. Кроме того, данные материалы не получают таких больших удлинений как пластичные и по времени разрушаются гораздо быстрее. На диаграмме хрупких материалов уже на первом участке имеется ощутимое отклонение от прямолинейной зависимости между нагрузкой и удлинением (напряжением и деформацией), так что о соблюдении закона Гука можно говорить достаточно условно. Так как пластических деформаций хрупкий материал не получает, то в ходе испытания не определяют предела текучести. Не имеет особенного смысла также рассчитывать и относительное сужение образца, так как шейка не образуется и диаметр после разрыва практически не отличается от исходного.

Влияние скорости деформации и температуры на прочностные характеристики

Стандарты на проведение испытаний на статическое растяжение, как правило, ограничивают скорость деформации или скорость приложения нагрузки. Так, стандарт ASTM E-8 ограничивает скорость деформации величиной 0,03 — 0,07 мм/мин. Такое ограничение вызвано искажением результатов за счёт повышения прочности металлов с ростом скорости деформации (при постоянной температуре). При скоростях деформации до 1 сек скорость деформации практически не влияет на прочностные характеристики (в частности, на предел текучести).

В общем виде можно выразить формулу влияния скорости деформации на предел текучести в виде:

где — скорость деформации; — астотный фактор, — активационный объём; — напряжение течения; — экстраполяция напряжения течения на нулевую скорость деформации.

Эта же зависимость даёт и зависимость напряжения течения от температуры. В области низких температур и при отсутствии фазовых превращений прочность кристаллических материалов повышается. Вклад в повышение прочности даёт и переход от термически активируемого процесса деформации за счёт движения дислокаций к механизму деформации путём двойникования.

Источник

диаграмма растяжения

3.2.1 диаграмма растяжения (tensile diagram): Зависимость между удлинением и нагрузкой вплоть до разрушения образца в режиме деформирования с постоянной скоростью.

Смотреть что такое «диаграмма растяжения» в других словарях:

Диаграмма растяжения — (tensile diagram): зависимость между удлинением и нагрузкой вплоть до разрушения образца в режиме деформирования с постоянной скоростью. Источник: Распоряжение Росавтодора от 16.07.2010 N 468 р Об издании и применении ОДМ 218.5.006 2010… … Официальная терминология

диаграмма — 3.1.3.27 диаграмма: Условное графическое изображение числовых величин или их соотношений, выполненное с помощью линий, плоскостей, геометрических фигур, рисунков. Источник … Словарь-справочник терминов нормативно-технической документации

ДИАГРАММА — графический способ изображения, наглядно показывающий какое либо явление, состояние, взаимосвязь или соотношение между различными величинами (напр. (см.), Д. растяжения или состояния сплава) … Большая политехническая энциклопедия

диаграмма деформации — [stress strain diagram] графическое изображение зависимости силовых характеристик материала (напряжение, истинное напряжение и т. п.) от деформации (удлинение, сужение, истинное удлинение и т. п.) при конкретных условиях испытаний. Различают… … Энциклопедический словарь по металлургии

Диаграмма — так называется кривая линия, вычерчиваемая самопишущим прибором, предназначенным для измерения какой либо величины, изменяющейся с течением времени. Таковы Д. индикатора (см.), ординаты которых выражают движение пара в паровом цилиндре, а… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Диаграмма (граф.) — так наз. кривая линия, вычерчиваемая самопишущим прибором, предназначенным для измерения какой либо величины, изменяющейся с течением времени. Таковы Д. индикатора (см.), ординаты которых выражают движение пара в паровом цилиндре, а абсциссы… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Рабочая диаграмма арматуры — – кривая растяжения арматуры, изображенная в прямоугольных координатах, с указанием на абсциссе деформаций в %. а на кординате напряжений в МПа; на кривой указываются точки, соответствующие напряжениям. [Терминологический словарь по бетону… … Энциклопедия терминов, определений и пояснений строительных материалов

ДЕФОРМИРОВАНИЯ ДИАГРАММА — графич. изображение зависимости между напряжениями (или нагрузками) и деформациями материала (или перемещениями при деформировании). Каждому виду нагружения присуща своя Д. д., поэтому различают диаграммы растяжения, сжатия, сдвига, изгиба,… … Большой энциклопедический политехнический словарь

Статическое растяжение — Машина для испытаний на растяжение с электромеханическим приводом Статическое растяжение одно из наиболее распространённых видов испытаний для определения механических свойств материалов … Википедия

ОДМ 218.5.006-2010: Рекомендации по методикам испытаний геосинтетических материалов в зависимости от области их применения в дорожной отрасли — Терминология ОДМ 218.5.006 2010: Рекомендации по методикам испытаний геосинтетических материалов в зависимости от области их применения в дорожной отрасли: 3.3.3 агрессивная среда (aggressive substance): Среда, вызывающая разрушение материалов и… … Словарь-справочник терминов нормативно-технической документации

Источник

Испытания материалов на растяжение. Диаграмма растяжения

При проектировании строительных конструкций, машин и механизмов инженеру необходимо знать значения величин, характеризующих прочностные и деформационные свойства материалов. Их можно получить путем механических испытаний, проводимых в экспериментальных лабораториях на соответствующих испытательных машинах. Таких испытаний проводится много и самых различных – испытания на твердость, сопротивляемость ударным и переменным нагрузкам, противодействие высоким температурам и т.д. Подробное описание всех видов механических испытаний и применяемых при этом машин и приборов приводится в специальной литературе. Мы же рассмотрим лишь испытания металлов на растяжение.

Наибольшую информацию о механических свойствах металлов можно получить из статических испытаний на растяжение. Испытания проводятся в соответствии с ГОСТом.

Испытания проводят на разрывных или универсальных машинах. В зависимости от метода приложения нагрузки машины бывают с механическим или гидравлическим приводом. Они обычно выпускаются с вертикальным расположением образца. Передача усилия на образец осуществляется через захваты. Разрывная машина снабжена устройством для автоматической записи в определенном масштабе диаграммы растяжения, т.е. графика зависимости между растягивающей силой Р и удлинением образца Dl. На рис.27 представлена диаграмма растяжения образца из низкоуглеродистой стали.

В начальной стадии нагружения до некоторой точки А диаграмма растяжения представляет собой наклонную прямую, что указывает на пропорциональность между нагрузкой и деформацией – справедливость закона Гука.

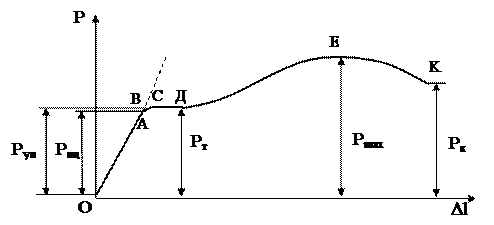Нагрузка, при которой эта пропорциональность еще не нарушается, на диаграмме обозначена Р_пц и используется для вычисления предела пропорциональности:

s_пц=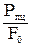, (47)

где F₀ – начальная площадь поперечного сечения образца.

Пределом пропорциональности s_пц называется наибольшее напряжение, до которого существует прямо пропорциональная зависимость между нагрузкой и деформацией.

Зона ОА называется зоной упругости. Здесь возникают только упругие, очень незначительные деформации. Данные, характеризующие эту зону, позволяют определить значение модуля упругости Е, как тангенс угла наклона этой прямой.

После достижения предела пропорциональности деформации начинают расти быстрее, чем нагрузка, и диаграмма становится криволинейной. На этом участке в непосредственной близости от точки А находится точка В, соответствующая пределу упругости:

s_уп=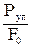. (48)

Пределом упругости s_уп называется максимальное напряжение, при котором в материале не обнаруживается признаков пластической (остаточной) деформации.

У большинства металлов значения предела пропорциональности и предела упругости незначительно отличаются друг от друга. Поэтому обычно считают, что они практически совпадают.

При дальнейшем нагружении криволинейная часть диаграммы переходит в почти горизонтальный участок СД – площадку текучести. Здесь деформации растут практически без увеличения нагрузки. Нагрузка Р_т, соответствующая точке Д, используется при определении физического предела текучести:

s_т=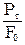. (49)

Пределом текучести s_т называется напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки.

Предел текучести является одной из основных механических характеристик прочности металлов.

Зона ВД называется зоной общей текучести. В этой зоне значительно развиваются пластические деформации. При этом происходит изменение внутренней структуры металла, что приводит к его упрочнению. Диаграмма после зоны текучести снова становится криволинейной, образец приобретает способность воспринимать возрастающее усилие до значения Р_max – точка Е на диаграмме. Это усилие используется для вычисления временного сопротивления или предела прочности:

s_в=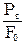. (50)

Пределом прочности называется напряжение, соответствующее максимальной нагрузке, достигнутой в ходе испытаний.

Зона ДЕ называется зоной упрочнения. Здесь удлинение образца происходит равномерно по всей его длине, первоначальная цилиндрическая форма образца сохраняется, а поперечное сечение изменяется незначительно, но также равномерно.

При максимальном или несколько меньшем усилии на образце в наиболее слабом месте возникает локальное уменьшение поперечного сечения – шейка. Дальнейшая деформация происходит в этой зоне образца. Сечение в середине шейки продолжает быстро уменьшаться, но напряжения в этом сечении все время растут, хотя растягивающее усилие и убывает. Вне области шейки напряжения уменьшаются, и поэтому удлинение остальной части образца не происходит. Наконец, в точке К образец разрушается. Сила, соответствующая точке К, называется разрушающей Р_к, а напряжения – истинным сопротивлением разрыву:

S_к=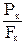, (51)

где F_к – площадь поперечного сечения в месте разрыва.

Зона ЕК называется зоной местной текучести.

Помимо указанных характеристик прочности определяют характеристики пластичности.

Относительное удлинение после разрыва d (%) – это отношение приращения расчетной длины образца после разрыва к ее первоначальному значению, вычисляемое по формуле:

%. (52)

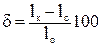
Заметим, что относительное удлинение после разрыва зависит от отношения расчетной длины образца к его диаметру. С увеличением этого отношения значение d уменьшается, так как зона шейки (зона местной пластической деформации) у длинных образцов занимает относительно меньше места, чем в коротких образцах. Кроме того, относительное удлинение зависит и от места расположения шейки (разрыва) на расчетной длине образца. При возникновении шейки в средней части образца местные деформации в области шейки могут свободно развиваться и относительное удлинение будет больше, чем в случае, когда шейка возникает ближе к головке образца, тогда местные деформации будут стеснены.

Другой характеристикой пластичности является относительное сужение после разрыва y (%), представляющее собой отношение уменьшения площади поперечного сечения образца в месте разрыва к начальной площади поперечного сечения образца:

%. (53)

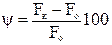
Диаграмма растяжения характеризует свойства образца, так как зависит от его размеров. Для оценки механических свойств материала диаграмму растяжения перестраивают в координатах «напряжение-деформация»: все ординаты делят на первоначальную площадь поперечного сечения F₀, а все абсциссы – на первоначальную длину рабочей части l₀. В результате получаем диаграмму напряжений, которая имеет тот же вид, что и диаграмма растяжения, так как F₀ и l₀ постоянны. Эта диаграмма является условной, поскольку при ее построении не учитывается изменение значений F₀ и l₀ в процессе испытания.

Поэтому определенные ранее пределы пропорциональности, текучести и прочности являются условными. Истинные же напряжения в каждый момент нагружения будут больше условных. Заметное отклонение истинных напряжений от условных происходит после предела текучести, так как сужение сечения становится более значительным. Особенно сильно возрастает разница между напряжениями после образования шейки. Диаграмма напряжений, построенная с учетом сужения площади поперечного сечения и местного увеличения деформаций, называется диаграммой истинных напряжений.

Некоторые диаграммы растяжения не имеют ярко выраженной площадки текучести, например, для низколегированных сталей, сплавов алюминия (рис.28). В этих случаях вместо физического предела текучести определяют условный предел текучести s_0,2 (точка Д) – напряжение, при котором остаточное удлинение достигает 0,2% от рабочей длины образца.

Источник