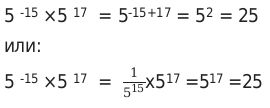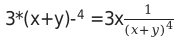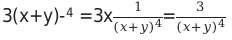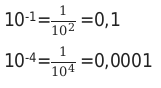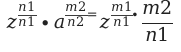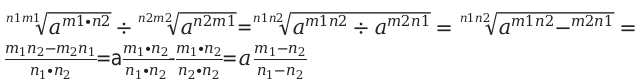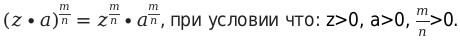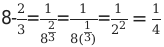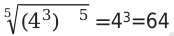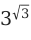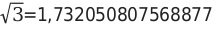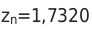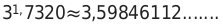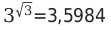Что такое степень с действительным показателем
1.1.7 Свойства степени с действительным показателем
Видеоурок 1: Степень с рациональным и действительным показателями. Часть 1
Видеоурок 2: Степень с рациональным и действительным показателями. Часть 2
Лекция: Свойства степени с действительным показателем
При рассмотрении степеней с действительным показателем в показателе может быть абсолютно любое значение, а, значит, при работе с такими степенями следует использовать следующие свойства.

Если в основании степени лежит положительное число, а в качестве показателя используются действительные числа, то можно пользоваться следующими формулами:
1. Так как в основании степени используется положительное число, то, несмотря на знак показателя степени, результат всегда будет числом положительным.
2. Если показатель степени является отрицательным числом, то его можно заменить на равный по модулю положительный показатель, а основание дроби перевернуть.
3. При умножении чисел с одинаковыми основаниями, действительные показатели степени следует сложить.
4. При делении чисел с одинаковыми основаниями, действительные показатели степени вычитаются:
5. При возведении числа в степени в дополнительную степень показатели умножаются.
7. При возведении частного некоторых чисел в действительную степень можно возвести каждое число по отдельности в данную дробь и только после этого разделить.
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №17. Степень с рациональным и действительным показателем.
Перечень вопросов, рассматриваемых в теме
2) определение степени с рациональным и действительным показателем;
3) нахождения значения степени с действительным показателем.
Если n- натуральное число, 



При любом действительном х 


Но если основание степени а=0, то степень 

При 

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Пример: вычислим
Мы можем представить 
Таким образом, мы можем записать

На основании данного примера можно сделать вывод:
Если n- натуральное число, 



Таким образом, степень определена для любого рационального показателя r и любого положительного основания а.
Если 




Пользуясь формулой 
Рассмотрим несколько примеров:
Отметим, что все свойства степени с натуральным показателем, которые мы с вами повторили, верны для степени с любым рациональным показателем и положительным основанием, а именно, для любых рациональных чисел p и q и любых 

Разберем несколько примеров, воспользовавшись данными свойствами:
В числителе вынесем общий множитель ab за скобки, в знаменателе представим корни в виде дробных показателей степени:
А теперь дадим определение степени с действительным показателем, на примере 
Пусть 

Эта последовательность стремится к числу 
Числа 

Можно сделать вывод, что данная последовательность стремится к некоторому действительному числу, которое обозначают 

Опредление степени с действительным показателем.
При любом действительном х 


Но если основание степени а=0, то степень 

При 

Для степени с действительным показателем сохраняются все известные свойства степени с рациональным показателем, из которых следует теорема.
Теорема. Пусть 


По условию 
а^(х₂)




Из данной теоремы вытекают три следствия:


Эти теорема и следствия помогают при решении уравнений и неравенств, сравнении чисел.
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Сравнить числа
Сравним показатели
Степень числа: определения, обозначение, примеры
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).
Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 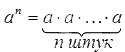
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0
При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как
При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
и так далее (при этом сами приближения являются рациональными числами).
Основные определения и свойства степеней в математике
Время чтения: 30 минут
В предложенном материале мы подробно будем изучать степени, их свойства. И постараемся весь изученный материал усвоить на примерах.
В этой статье мы подробно изучим, что такое степень числа. Разберемся и охарактеризуем определения степени числа. При этом выучим все существующие в математике показатели степени. Начиная от натурального числового показателя, заканчивая рациональным показателем.
Весь материал попутно будем рассматривать, и закреплять на конкретных примерах.
Перед тем, как приступить к изучению основных свойств степеней, разберем следующие основные определения, которые нам понадобятся в процессе всего изучения материала определения:
Степень числового значения — это перемноженные между собой одинаковые значения.
Разберем данное определение на примерах:
Левую часть равенства можно упростить. Для начала указать множитель, который повторяется, и обозначить количество его повторений. Повторяющийся множитель в данном случае это 2. Дублируется он три и шесть раз соответственно. Поэтому над двойкой записываем 3 и 6:
Формулировка выражений звучит следующим образом:
Основание выражения степени — это числовое или буквенное значение, которое повторяется в выражении не однократно.
В вышеизложенных выражениях — это число два.
Показатель степени — это значение, которое отображает, количество повторений основания степени.
В примере, мы видим, что число 5 и 6 повторяется три раза, так как степень, в которую нужно возвести число равняется трем.
Если степень, будет иметь иное значение. Например: 7, то показатель степени будет равняться семи.
Иными словами, приведенный расчет называется приведением в степень.
Например: нам необходимо определить произведение пяти одинаковых чисел, каждый из них равен 3, то правильно будет сказано, что число 3 возводится в пятую степень:
Видим, что число три в пятой степени равняется числу 243.
Для закрепления разберем еще несколько простых примеров.
Пример 1.
Пример 2.
Пример 3
Степени, так же подразделяются на:
В алгебре, да и, в общем, в математике, степень, как правило, имеет четыре основных свойства:
В данном уроке, мы поочередно разберемся с каждым свойством, его особенностями расчетов. Закрепим материал на конкретных примерах с применением числовых данных.
Свойство степени с натуральным показателем и особенности вычисления
Натуральный показатель степени имеет следующие свойства:
а) Главное свойство:
Равенство является верным при любых значениях m и n. И действительном значении а.
Равенство мы разберем на конкретном числовом примере:
Мы имеем две степени с основание четыре.
Натуральные показатели имеют значения три, и пять соответственно.
Составим равенство, подставляя числовые значения:
4 3 x4 5 =(4·4·4)(4·4·4·4·4)=64×1024=65536 или 4 8 =4·4·4·4·4·4·4·4=65536
Решив равенство, мы получаем: 4 3 4 5 =4 8
Тем самым, мы видим, что равенство доказано.
Также, используя свойство умножения, можно обобщить свойства. Если в равенстве представлены от трех и более степеней. Натуральные числа обозначим m1, m2.
Составим несколько равенство, подставляя числовые значения, для лучшего усвоения:
(2) 2 (2) 3 (2) 3 (2) 4 =(2) 2+3+3+4 =(2) 12
(3) 2 (3) 3 (3) 3 (3) 4 =(3) 2+3+3+4 =(3) 12
(5) 2 (5) 3 (5) 3 (5) 4 =(5) 2+3+3+4 =(5) 12
б) Свойство частных степени, когда основания имеют одинаковые значения
Свойство частных имеет следующий вид, в виде равенства:
Оно справедливо при любых натуральных значений n и m, любом значении x, кроме нуля. Значение основания, нельзя принимать равным нулю. В противном случае при расчете, придется делить на ноль, что по правилам математики недопустимо.
Так же, есть еще одно условие: значение n должно быть больше, значения m. После вычета должно получится положительное число.
Для доказательства условия, составим равенство:
x n-m x m =x (n-m)+m =x n
Преобразовав равенство, мы можем вывести следующий пример:
Для наглядности, подставим числовые значения:
в) Произведение степеней
Степень произведения можно выразить в виде равенства:
Равенство можно преобразовать в следующей вид:
(xy) m =(xy)(xy). (xy), количество множителей равно числовому значению степени.
Рассмотрим несколько равенств с числовыми значениями:
— Вариант для положительных значений:
— Вариант для дробей:
— Вариант отрицательных значений:
г) Возведение частного в натуральную степень.
Составим равенство для доказательства данного свойства.
Должны соблюдаться следующие условия:
Для доказательств равенства распишем пример:
Для закрепления знаний, решим несколько примеров, заменяя буквенные значения числовыми.
д) Принцип возведения степени в степень
(2 5 ) 4 =2 5 x 4 =2 20
Также, данное свойство, может быть выражено и несколькими степенями, в виде:
((((x n ) b ) a ) m =x n·x·b·a·m
Для решения равенства, такого типа, необходимо перемножить между собой значение степеней.
((((32) 3 ) 4 ) 2 =3 2342 =3 48
((((5) 3 ) 4 ) 2 =5 2342 =5 48
((((12) 3 ) 4 ) 6 =3 2346 =3 192
е) Принципы равенства и неравенства.
Данный принцип звучит следующим образом: большее значение имеет степень, у которой значение основания степени большее или наоборот.
Например:
x 2 2 или подставив числовые значения, образует вид: 4 5 5
Еще несколько примеров для закрепления, с разными числовыми значениями:
Как видно из примеров, равенство верно, в том случае если значение основания больше.
Принцип неравенства считается верным, если одна степень больше значения другой, а основание больше нуля, но не меньше единицы. То есть, числовое значение должно быть положительным.
Степень с целым показателем и ее свойства
После того как мы определили степень числа с натуральным показателем, мы можем дальше продолжать расширять знания о степени и перейти к степени числа, показателем которой является любое число, в том числе и отрицательное и ноль. Из этого следует, чтобы оставались правильными все свойства степени, потому что натуральные числа являются составляющей целых чисел.
Степень с целым показателем — это степень, когда любое целое число, является показателем.
Натуральный вид степени тоже является степенью с целым показателем, потому что натуральные числовые значения так же являются целыми числами.
Для степеней с целыми положительными показателями, свойства аналогичны, как и для натуральных показателей.
Рассмотрим основные свойства степеней с целыми показателями.
Рассмотрим следующую последовательность степеней:
3 0 3 1 3 2 3 3 3 4 3 5 3 6 3 7
Продолжим решать значения с отрицательными степенями:
Теперь определим степени с натуральным значением и с нулем.
Расчеты приведены в таблице 1
Таблицы 1. Расчет степени с натуральными показателями и с нулем
| Значение степени | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Результат вычисления | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Если вычисление положительных значений и нуля, особых трудностей не вызывает. А что делать с отрицательными показателями? На этот вопрос мы ответим далее.
При возведении в положительную степень, как правило, число имеет большее значение. А вот при вычислении в отрицательной степени, результат будет иметь меньшее значение.
Если для примера взять число z, и начать поочередно увеличивать его степень, то в результате мы увидим поочередность чисел, где последующее число меньше следующего в z раз.
Для примера, возьмем число 4.Начало расчета возьмем ноль и будем поочередно повышать степень. Далее найдем значение при вычислении.
Расчеты приведены в таблицу 2.
Таблицы 2. Расчет степени с натуральными показателями.
| Значение степени | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Результат вычисления | 1 | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 |
Получили перечень чисел, в котором каждое число больше предыдущего числа в четыре раза. Тогда правильно предположить, что число, которое имеет значение больше единицы, будет в четыре раза больше единицы.
Предыдущее за числом 1/4 должно быть в два раза меньше. Чтобы его получить разделим 1/4 на 2.
Отсюда следует, что 1/4>1/16 в четыре раза.
Выполняя деление на четыре определим значения других степеней с целыми отрицательными показателями:
Расчеты приведены в таблицу 3.
Таблицы 3. Расчет степени с целыми отрицательными значениями степеней.
| Значение степени | -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| Результат вычисления | 1 | 4 | 16 | 64 | 256 | 1024 | 16384 |
Проанализировав значения в таблице 3, можно сделать следующий вывод: результаты степени с отрицательными значениями, прямо пропорциональны значениям с положительным результатом.
Данные вычисления и сравнения сведем в таблицу 4.
Таблица 4. Сравнение и анализ итоговых данных.
| -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| 1 | 4 | 16 | 64 | 256 | 1024 | 16384 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 |
Решим еще несколько примеров для закрепления материала.
Воспользуемся, уже изученным правилом вычисления значения степеней, у которых значение отрицательное.
Потому что, если z будет равен нулю, в знаменателе число выйдет равным ноль. По правилам математики на ноль делить нельзя.
1.Принцип вычисления тождественных преобразований
Все данные преобразования для натуральных и целых показателей одинаковы. Они, также, сохраняются и для степеней, которые имеют отрицательные значения.
Далее, при помощи примеров, закрепим полученные знания
Пример 1. Найти значение выражения 5 −15 × 5 17
Вариант вычисления, первым способом, легче. Именно его чаще всего и применяют в процессе обучения.
Пример 2. Найти значение выражения (10−4)−1
Используем для расчета правило возведения в степень
(10 −4 ) −1 = 10 −4 × (−1) = 10 4 = 10000
Пример 3. Определить значение выражения (10 −5 ) −1
Для этого применим правилом возведения степени в степень:
(10 −5 ) −1 = 10 −5 × (−1) = 10 5 = 10000
2.Перемещение степени между знаменателем и числителем
В случае если в знаменателе дроби, имеется степень, то ее можно переместить в числитель и при этом необходимо поменять знак на противоположный.
При этом само значение выражения не поменяется.
Данный метод иногда используется при упрощении выражений.
Рассмотрим основные примеры:
Пример 1.
Пример 2. Перемещение значения степени из знаменателя дробного выражения 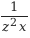
Пример 3. Записать произведение 3x*(x + y) −4 в виде дроби, которая не имеет степени с отрицательным значением.
Затем перемножим множитель 3 с числителем дроби 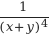
Итоговый результат:
3.Возведение числа 10 в целую отрицательную степень
Вычисление степени для числа 10 происходит таким же образом, как и остальные числа.
На примерах рассмотрим более подробно.
Пример 1:
Если обратить внимание на пример, то мы увидим, что количество нулей в ответе равно показателю самой степени.
Проще говоря, чтобы возвести 10 в отрицательную степень, можно только записать количество необходимых нулей перед единицей. Но, не забыть поставить запятую, перед вторым нулем.
Пример 1:
Пример 2:
Пример 3:
Пример 4:
Пример 5:
4.Преобразование значений 0,1, 0,01, 0,001, где основанием степени является число 10
Если степень представлена числами 0,1; 0,01; 0,001 и основание имеет значение 10. Для преобразования необходимо:
Число 0,01 это значение деления 1/100, или 1/10 2
Пример 2: Значение 0,00001 в виде степени с основанием 10.
5. Вид числа (значения) стандартный
Запишем число 4 000 в следующем виде 4 и 1 000
Именно такое выражение и называют стандартным видом. Он позволяет записывать большие и маленькие числа в более компактном виде.
Пример 1.
Пример 2.
0,158× 10 000 = 0,158× 10 4
Пример 3.
26× 1 000 000 = 26× 10 6
Стандартный вид числа имеет следующее выражение: z × 10m, где 1 ≤ z Нужна помощь
Свойство степени с рациональным показателем
От целых показателей степени числа z мы переходим к рациональным показателем степеням. Далее мы определим степень с рациональным показателем, причем будем производить расчеты так, чтобы сохранялись все свойства степени с целым показателем. Это обязательно, потому что целые числа являются непосредственно частью рациональных чисел.
Свойство степени с рациональным показателем значительно облегчает изучение степеней в целом. Изучив данный метод, можно легко научится решать задачи различного уровня сложности.
Рассмотрим основные свойства степени с рациональным показателем.
а) Произведение степеней с основаниями, которые имеют одинаковые значения.
б) Свойство частного значения.
Доказательство данного свойства идентично по сравнению с предыдущим.
в) Свойство произведения в степень в виде дроби
г) Свойство степени в степени.
д) Свойство сравнения степеней со значениями равными между собой
Отсюда следует неравенство: m m >y m
е) Условие рациональных чисел
x > y при 0 0 z x >z y
Для того чтобы доказать все перечисленные условия, нам необходимо будет вспомнить, понятие степени с дробным показателем.
Рассмотрим свойство с рациональным показателем на примере:
Пример №1.
Пример № 2: необходимо вычислить
Преобразуя уравнение, мы получим следующий вид: 4 15 =(4 3 ) 5 далее записываем в виде
Степень с иррациональным и действительным показателем
Понятно, что множество действительных чисел можно рассматривать как объединение множеств рациональных и иррациональных числовых значений. Поэтому степень с действительным показателем принято считать определенным значением, когда определяются степень с рациональным показателем и степень с иррациональным показателем. Про степень с рациональным показателем было подробно рассмотрено в предыдущем пункте, осталось лишь разобраться подробнее со степенью с иррациональным показателем.
Основные свойства иррациональных чисел:
— сумма из двух положительных иррациональных чисел может равняться рациональным числом.
— множество иррациональных чисел встречаются повсюду на протяжении всей числовой прямой
— между двумя любыми различными рациональными числами имеется иррациональное число.
Свойства иррациональных степеней, как было уже сказано ранее, включают в себя все предыдущие характеристики с других свойств степеней
1. a p ⋅ a q = a p + q ;
2. a p : a q = a p – q ;
3; ( a ⋅ b ) p = a p ⋅ b p ;
4.( a : b ) p = a p : b p ;
6. a p q a p =0 a>0, то a p > a q a p >a q ;
Таким образом, все степени, показатели которых p p и q q являются действительными числами, при условии
a > 0 a>0 обладают теми же свойствами.
Для определения степени с иррациональным показателем, часто конечный результат определяют с точностью до определенного знака.
Для того, чтобы вычислить число в иррациональной степени, нужно его число возвести в дробную степень.
Более точный результат мы получим, при наиболее приближенном значении.
Рассмотрим на примере:
— Вычислим значение корня из 3.
— Определим приближенное значение до четырех цифр после запятой.
— Возведем значение три в степень и получим значение, в виде бесконечной дроби:
— Далее необходимо округлить полученное числовое значение до четырех знаков.
Иррациональный процесс расчета, метод очень трудоемкий. В основном все вычисления в алгебре строятся таким методом, чтобы избавиться от иррациональности. Он несет в себе неудобства расчета, ведь иррациональность не дает возможность получить точность определения окончательного значения.