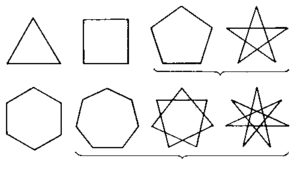
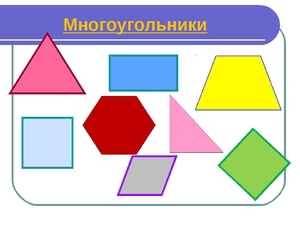
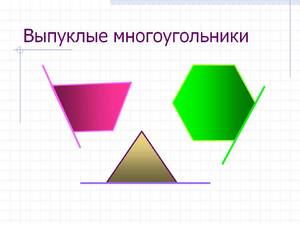
Что такое правило многоугольника в геометрии

Сложение и вычитание векторов – правила

Сложение и вычитание векторов – это одно из немногих действий на стыке математики и геометрии. Дело в том, что выражения из векторов можно складывать и вычитать арифметически, ориентируясь только по буквенным обозначениям отрезков, но для того, чтобы получить числовой результат или его геометрическое отображение придется выполнить ряд построений. Разберемся подробнее в правилах сложения и вычитания векторов.

Что такое вектор?

Вектор это образок с направлением.

Вектор и луч часто путают и допускают грубую ошибку. Вектор то направленный отрезок, а любой отрезок имеет величину, то есть его можно измерить линейкой. Луч имеет начало и направление, но он бесконечен, то есть измерить его невозможно. Так же, как нельзя и складывать лучи между собой или луч с вектором.

Вектор иногда помещают в декартову систему координат. Тогда проведя перпендикуляры к каждой из осей, можно получить проекции вектора на оси х и у. Каждая из этих проекций будет отрезком. При этом, если из проекций составить прямоугольник, то его гипотенуза и будет начальным вектором. Это иногда используется при сложении векторов.

Рис. 1. Вектор в системе координат.

Сложение и вычитание векторов

Способов и методов сложения векторов всего два. Существует и третий, но его не считают отдельным методом, так как он проистекает из первых двух. Но мы его рассмотрим отдельно, чтобы не возникало вопросов при дальнейшем изучении темы.

Правило многоугольника

Для того, чтобы сложить вектора правилом многоугольника, необходимо параллельным переносом совместить конец первого вектора с началом второго, конец второго с началом третьего и так далее, пока не кончатся вектора, которые необходимо складывать.

После этого нужно конец последнего вектора соединить с началом первого и указать направление. Получившийся вектор будет направлен в сторону последнего из учавствовавших в сложении.

Складывать таким способом можно любое количество векторов. Если так складывается только два вектора, то способ называют правилом треугольника

Нужно понять и запомнить, что у отрезка одна определяющая величина: размер. У вектора определяющих величин две: размер и направление. Поэтому нельзя менять направление вектора и его размер. Любые действия нужно осуществлять с помощью параллельного переноса, то есть без изменения направления.

Рис. 2. Правило многоугольника.

Правило параллелограмма

Правило параллелограмма сложнее, его можно применять только для 2 векторов. Если вам нужно этим способом сложить большее количество векторов, например, три, то действие выполняют в следующем порядке:

Само правило параллелограмма заключается в том, что начала двух векторов совмещаются. После этого получившуюся фигуру достраивают до параллелограмма. Диагональ, которая выходит из начала двух векторов и есть результат сложения. Вектор должен быть направлен в противоположную сторону от совмещенного начала двух векторов.

Для того чтобы вычесть вектора любым способом, направление вектора, который является вычитаемым, меняют на противоположное. Получившиеся вектора складывают любым из методов.

Рис. 3. Правило прямоугольника.

Сложение в декартовой системе

В декартовой системе все вектора раскладывают на проекции, после чего отрезки проекций складывают: проекции на ось х отдельно, на ось у отдельно. После из получившихся двух проекций снова собирают вектор.

Что мы узнали?

Мы узнали, что такое вектор. Поговорили о правилах сложении и вычитании векторов. Обсудили, чем отличается вектор от луча и обсудили метод действий с векторами в декартовой системе координат.

Источник

Геометрическая фигура многоугольник

Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.

Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.

Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.

Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.

Основные понятия

Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:

Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:

Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.

Виды фигур

Треугольник

Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.

Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.

По соотношениям между сторонами все треугольники можно подразделять на несколько видов:

Кроме того, принято различать следующие треугольники:

Четырехугольник

Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.

На одной прямой не может находиться сразу три вершины четырехугольника.

Видео

Дополнительную информацию о многоугольниках вы найдете в этом видео.

» width=»560″ height=»314″ allowfullscreen=»allowfullscreen»>

Источник

Многоугольник

Всего получено оценок: 265.

Всего получено оценок: 265.

Многоугольников в математике 5 класса достаточно много. Только самые популярные из них имеют названия. Разберем наиболее часто встречающиеся виды многоугольников.

Что такое многоугольник?

На самом деле многоугольником может считаться вообще любая фигура. Как плоская, так и объемная. Ведь в любой фигуре количество углов больше или равняется 3. Многоугольники делятся на выпуклые и невыпуклые. Определяется этот параметр следующим способом: через каждую сторону проводят прямую. Если для каждой прямой фигура лежит по одну сторону от прямой, то многоугольник называется выпуклым.

В школьном курсе нет ни одной теоремы для невыпуклых многоугольников. Далеко не каждый профессор математики может вспомнить хотя бы одну такую теорему. Дело в том, что в жизни невыпуклые треугольники не встречаются и решать задачи на них просто не имеет смысла. Но знать о разделении многоугольников по такому признаку – обязательно.

Виды многоугольников

Простейшие многоугольники делятся по количеству углов:

На самом деле называть можно продолжать до бесконечности, но даже пятиугольник уже редко встречается в решении задач, при его решении зачастую приходится использовать уравнения.

Пятиугольник редко встречается и в строительстве, физике и прочих науках. В любом случае, если ученику требуется решить пятиугольник, его нужно разбить на треугольники и работать с привычными фигурами. А на треугольники можно разбить вообще любую плоскую фигуру.

Треугольник

Треугольник не просто простейший многоугольник, это одновременно и основа большей части известной геометрии. Все неизвестные плоские фигуры при решении разбивают на треугольники. Для этой фигуры открыто больше всего теорем, характеризующих точек, отрезков и пропорций. В Америке существует целая энциклопедия треугольников.

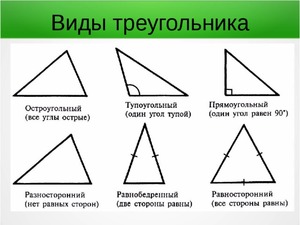
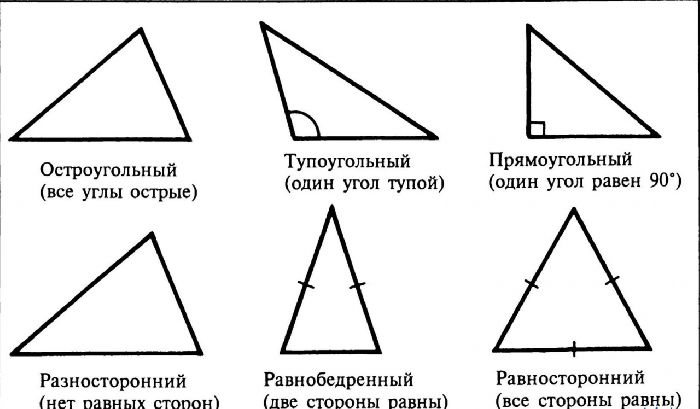
В зависимости от входящих в состав треугольника углов, фигуры подразделяются на:

В зависимости от сторон треугольники делятся на:

Особенное внимание нужно уделять правильному определению видов треугольников. Многие теоремы созданы для специального вида треугольников и не будут работать с другими.

Рис. 2. Виды треугольников.

Четырехугольник

Четырехугольник имеет не меньшее количество разновидностей, чем треугольник. Но основных всего две, это параллелограмм и трапеция.

Параллелограммом называют выпуклый четырехугольник, у которого стороны попарно равны и параллельны. Обратите внимание, что в определении треугольника никогда не используют параметр «выпуклый», о котором мы говорили в начале. Дело в том, то треугольники всегда выпуклые, а вот уже четырехугольники могут быть и невыпуклыми.

Параллелограмм в зависимости от равенства элементов: углов и сторон – подразделяется на следующие фигуры:

Все эти, привычные нам, фигуры являются разновидностями параллелограммов.

Рис. 3. Виды параллелограмма.

Трапецией зовется четырехугольник, у которого две стороны параллельны, а две нет. При этом существует множество четырехугольников, которые не входят ни в одну из групп. Такие фигуры называют произвольными четырехугольниками.

Необычные многогранники

Помимо названных фигур, существует и множество других. Количество углов в многоугольнике может быть бесконечно велико, но встречаются такие фигуры только при использовании правила многоугольника. Это правило используют при сложении вектором.

Существует отдельное понятие правильных многоугольников, то есть фигур, у которых все стороны и углы равны. Плоские фигуры в гранях объемных объектов образуют многогранники с замысловатыми названиями:

Что мы узнали?

Мы поговорили о многоугольниках. Выделили основные виды многоугольников, немного поговорили о каждом из видов. Рассказали, зачем нужно точно знать вид многоугольника, который прописан в условии задачи.

Источник

Многоугольники (ЕГЭ 2022)

Никогда не было интересно, почему в треугольнике 180 градусов?

А в других фигурах сколько? Да постой, положи транспортир!

Сейчас ты узнаешь много нового о такой, казалось бы, простой теме, как многоугольники.

Многоугольники — коротко о главном

Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,

Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.

Например: многоугольник c \( \displaystyle 4\) сторонами называют четырехугольником, многоугольник с \( \displaystyle 6\) сторонами — шестиугольником и так далее по аналогии.

Выпуклый многоугольник – многоугольник лежащий по одну сторону от любой прямой, соединяющей его соседние вершины.

Сумма внутренних углов выпуклого n-угольника равна \( \displaystyle 180<>^\circ \cdot (n-2)\) или \( \displaystyle <<\alpha >_<1>>+<<\alpha >_<2>>+\text< >…

Правильный выпуклый многоугольник – многоугольник все стороны и внутренние углы которого равны.

Внутренний угол правильного \( \displaystyle n\)-угольника равен \( \displaystyle \alpha =\frac\cdot 180<>^\circ \).

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

Центры вписанной в правильный многоугольник окружности и окружности, описанной около него, совпадают.

Если многоугольник такой, что в него можно вписать окружность, то его площадь выражается формулой: \( \displaystyle S=pr\), где \( \displaystyle p=\frac<<_<1>><_<2>>+<_<2>><_<3>>+…+<_><_<1>>><2>\).

Многоугольник — подробнее

Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,

При этом смежные стороны (имеющие общую вершину) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (то есть не должны пересекаться).

Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.

Произвольные многоугольники

Давай-ка нарисуем, какие бывают многоугольники.

А теперь вопрос: какой из этих многоугольников выпадает из ряда?

Посмотри внимательно на второй многоугольник — он отличается от всех остальных. Чем же?

Это не выпуклый многоугольник. Это, конечно, математическое название, но с человеческой интуицией не расходится.

Ну вот, а мы будем рассматривать только выпуклые многоугольники, то есть такие, как 1),3),4) и т.п.

Итак, основной факт:

В любом многоугольнике сумма внутренних углов равна \( \displaystyle 180^o(n-2)\), где буква «\( \displaystyle n\)» означает число углов многоугольника.

Давай сразу к примерам:

Четырехугольник

Пятиугольник

Шестиугольник

Ах да, про треугольник забыли.

Треугольник

Сумма углов многоугольника. Доказательство.

А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника \( \displaystyle 180^\circ(n-2)\).

Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.

Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.

Итак, давай разделим многоугольник на треугольники.

Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:

Всего вершин: \( \displaystyle n\)

Из вершины \( \displaystyle B\) можем провести диагонали во все вершины, кроме:

Значит всего диагоналей \( \displaystyle (n-3)\). А на сколько треугольников распался наш многоугольник?

Представь себе: на \( \displaystyle n-2\). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.

Итак, у нас ровно \( \displaystyle n-2\) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.

Чему равна сумма углов треугольника? Помнишь? Конечно \( \displaystyle 180<>^\circ \).

Ну вот, \( \displaystyle n-2\) треугольника, в каждом по \( \displaystyle 180<>^\circ \), значит:

Сумма углов многоугольника равна \( \displaystyle 180<>^\circ \)\( \displaystyle (n-2)\)

Что же из этого может оказаться полезным? Два момента:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Правильные многоугольники

Многоугольник называется правильным, если все его углы и все его стороны равны.

Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.

Первый вопрос:

А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?

Давай посмотрим на примере.

Пусть есть, скажем, правильный восьмиугольник:

Сумма всех его углов равна \( \displaystyle 180<>^\circ \left( 8-2 \right)=1080<>^\circ \).

А сколько всего углов? Восемь конечно, и они все одинаковые.

Значит любой угол, скажем \( \displaystyle \angle A\) можно найти:

\( \displaystyle \angle A=\frac<1080<>^\circ ><8>=135<>^\circ \).

Что мы еще должны знать?

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

При этом центры этих окружностей совпадают.

Смотри, как это выглядит!

И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.

Давай опять на примере восьмиугольника.

Посмотри на \( \displaystyle \Delta OKG\). В нем \( \displaystyle OK=r,OG=R.\)

Значит, \( \displaystyle \frac=\sin \angle x\) – и это не только в восьмиугольнике!

Чему же равен в нашем случае \( \displaystyle \angle x\)?

Ровно половине \( \displaystyle \angle G\), представь себе!

Значит \( \displaystyle \angle x=\frac<135<>^\circ ><2>=67,5<>^\circ \).

Смешно? Но так и есть! Поэтому для восьмиугольника \( \displaystyle \frac=\sin 67,5<>^\circ \).

Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки \( \displaystyle O\)?

И тот же ответ: конечно можно!

Опять рассмотрим наш восьмиугольник. Вот мы хотим найти \( \displaystyle \angle \alpha\) (то есть \( \displaystyle \angle HOG\)).

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

И так можно все находить не только для восьмиугольника, но и для любого правильного многоугольника.

Бонус. Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 6. Описанная окружность. Многоугольники

Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.

Около каких фигур можно, а вокруг каких нельзя описать окружность.

Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.

Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

А теперь твоя очередь!

Теперь ты знаешь все о многоугольниках!

Особенно эти знания пригодятся тебе, когда будешь решать задачи про окружности. Задачи олимпиадного уровня. Да и просто так знать полезно 🙂

А сейчас мы хотим услышать тебя. Понравилась ли тебе статья? Ты во всем разобрался?

Кстати, пытался строить многоугольники циркулем?

Напиши в комментариях ниже!

И задай любые вопросы, если они возникли! Мы непременно ответим!

Добавить комментарий Отменить ответ

3 комментария

Як разбить чатырох угольник так, чтоб палучился трохвугольник и чатырохвугольник

Даша, например, можно провести отрезок из вершины в середину противоположной стороны.

Некоторые комментарии прошлых лет к этой статье:

Сергей
19 февраля 2018
Просто огромное спасибо. Хоть что-то начал понимать.

Александр (админ)
19 февраля 2018
Просто огромное пожалуйста. 🙂 Очень приятно слышать от вас такие слова.

Вероника
18 марта 2020
Спасибо большое, а то на карантине приходится самим разбирать темы!

Александр (админ)
18 марта 2020
Отлично, Вероника! Круто, что ты сама пытаешься разобраться с математикой! Этот навык ой как пригодится в будущем. Я всегда говорю: «В жизни репетитора и учителя рядом не будет». И я рад, что наш скромный сайт в этом помогает. Удачи на экзаменах! Все будет хорошо!

Сима
01 июля 2020
Блин, действительно очень круто изложили. А главное- понятно и просто. Начала подготовку к егэ, в следующем году сдавать. Очень помогли разобраться с этой темой! Спасибо)

Александр (админ)
01 июля 2020
Блин, Сима, до чертиков приятно слышать такие слова! 🙂 Если начала подготовку к ЕГЭ, то будь на связи, мы сейчас делаем крутейший курс подготовки к ЕГЭ, где вот так вот просто все будет объяснять Алексей Шевчук.

Источник

Многоугольники

Замкнутая ломаная линия, которая состоит из нескольких звеньев-отрезков, называется многоугольником.

Если у замкнутой ломаной линии 4 звена-отрезка, это четырёхугольник.

У четырёхугольника 4 стороны и 4 вершины.

Четырёхугольники бывают разными.

Прямоугольник

Противоположные стороны прямоугольника равны между собой и ВСЕ углы прямые.

Свойства диагоналей прямоугольника:

1) Диагонали прямоугольника равны.

2) Точка пересечения диагоналей прямоугольника делит каждую диагональ пополам.

Квадрат

Прямоугольник, у которого все стороны равны и все углы прямые, называется квадратом.

При пересечении диагоналей квадрата получаются четыре прямых угла.

Трапеция

А этот четырёхугольник называется трапецией.

Ромб

А такой четырёхугольник называется ромбом.

Существуют и другие многоугольники, например, такой.

Ты видишь, что у него 8 вершин, значит, это восьмиугольник.

А у этого многоугольника 5 вершин. Это пятиугольник.

Поделись с друзьями в социальных сетях:

Источник