Что такое диаграмма венна
Диаграмма Венна
Диаграмма Венна — схематичное изображение всех возможных пересечений нескольких (часто — трёх) множеств. Если пересечения позволяется указывать не все, получается более общий случай — круги Эйлера.
Диаграммы Эйлера — Венна (как их ещё называют) изображают все 


Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.
Ссылки
Логические операции с понятиями
2 константы: импликация (
Полезное
Смотреть что такое «Диаграмма Венна» в других словарях:
ДИАГРАММА ВЕННА — ДИАГРАММА ВЕННА, схематическое представление отношений между математическими МНОЖЕСТВАМИ или логическими утверждениями, названное по имени английского логика Джона Венна (1834 1923). Множества изображаются в виде геометрических фигур, обычно… … Научно-технический энциклопедический словарь
диаграмма Венна — Иллюстрирующая логические операции и операции булевой алгебры Boolean algebra [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN Venn diagram … Справочник технического переводчика
диаграмма Венна — Venn o diagrama statusas T sritis automatika atitikmenys: angl. Venn diagram vok. Venn Diagramm, n rus. диаграмма Венна, f pranc. diagramme de Venn, m ryšiai: sinonimas – Veno diagrama … Automatikos terminų žodynas
ДИАГРАММА ЭЙЛЕРА — ДИАГРАММА ЭЙЛЕРА, простая диаграмма, используемая в логике для демонстрации силлогизмов. Классы предметов изображаются в виде кругов, и утверждения типа «Некоторое а находится в b» представляется двумя пересекающимися кругами, представляющими а и … Научно-технический энциклопедический словарь
Диаграмма Эйлера — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия
ВЕННА ДИАГРАММА — графический способ изображения формул математич. логики, прежде всего формул исчисления высказываний. В. д. ппеременных классич. логики высказываний представляет собой такой набор замкнутых контуров (го меоморфных окружностям), к рый разбивает… … Математическая энциклопедия
Диаграммы Венна — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия
Диаграммы Эйлера—Венна — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия
ДИАГРАММЫ ВЕННА — ДИАГРАММЫ ВEHHА графический способ задания и анализа логико математических теорий и их формул. Строятся путем разбиения части плоскости на ячейки (подмножества) замкнутыми контурами (кривьми Жордана). В ячейках представляется информация,… … Философская энциклопедия
Круги Эйлера — Пример кругов Эйлера. Буквами обозначены, например, свойства: живое существо, человек, неживая вещь Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения … Википедия
Диаграммы Венна
Что такое диаграмма Венна
Диаграмма Венна — это схема с пересекающимися кругами, которая показывает, как много общего имеют различные множества. Для построения диаграммы Венна выбирают несколько групп объектов и размещают их в отдельных кругах, при этом в область пересечения кругов попадают объекты, совмещающие в себе свойства данных множеств.
Приведем простейший пример. Допустим, у нас есть две группы объектов — световые устройства (обозначим их в первом круге) и энергосберегающие технологии (обозначим их во втором круге). В данном случае область пересечения кругов будет охватывать объекты, которые можно отнести и к первой, и ко второй группе, то есть энергосберегающие световые устройства.
Диаграммы Венна с успехом применяются в математике, логике, менеджменте и других прикладных областях для сопоставления каких-либо множеств и установления взаимосвязей между ними.
Единственный минус таких диаграмм — они могут быть использованы лишь для определения общих качеств рассматриваемых объектов и не дают информации о количестве объектов.
Диаграммы Венна: для чего они нужны
К диаграммам Венна прибегают для сравнения исходных данных в двух случаях:
Благодаря визуальной форме подачи информации и простоте расшифровки диаграммы Венна значительно облегчают процесс осмысления и анализа сравниваемых объектов. Именно поэтому они нашли широкое применение при проведении презентаций.
Рекомендации по созданию диаграмм Венна
Рисование диаграммы Венна — это совсем не сложный процесс, который включает всего четыре этапа:
Диаграмма Венна
Опубликовано 10.06.2020 · Обновлено 14.06.2021
Что такое Диаграмма Венна?
Диаграмма Венна – это иллюстрация, в которой круги используются для отображения отношений между вещами или конечными группами вещей. Перекрывающиеся круги имеют общие черты, в то время как круги, которые не перекрываются, не имеют этих черт.
Ключевые моменты
Понимание диаграммы Венна
Английский логик Джон Венн популяризировал диаграмму в 1880-х годах. Он назвал их кругами Эйлера в честь швейцарского математика Леонарда Эйлера, создавшего аналогичные диаграммы в 1700-х годах.
Термин диаграмма Венна не появлялся до 1918 года, когда Кларенс Льюис, американский академический философ и возможный основатель концептуального прагматизма, назвал круговое изображение диаграммой Венна в своей книге Обзор символической логики.
Краткая справка
Диаграммы Венна используются с середины 20-го века в классах от уровня начальной школы до вводной логики.
Венн изучал и преподавал логику и теорию вероятностей в Кембриджском университете, где он разработал свой метод использования диаграмм для иллюстрации раздела математики, известного как теория множеств.
Приложения для диаграмм Венна
Диаграммы Венна используются для отображения того, как элементы соотносятся друг с другом на общем фоне, вселенной, наборе данных или среде. Диаграмму Венна можно использовать, например, для сравнения двух компаний в одной отрасли, иллюстрируя продукты, предлагаемые обеими компаниями (где круги перекрываются), и продукты, которые являются эксклюзивными для каждой компании (внешние круги).
Примеры диаграмм Венна
Для иллюстрации фруктов красного или оранжевого цвета можно нарисовать диаграмму Венна. Ниже мы видим, что есть оранжевые фрукты (круг B), такие как хурма и мандарины, а яблоки и вишня (круг A) красного цвета. Перец и помидоры бывают красного и оранжевого цветов, что представлено областью перекрытия двух кругов.
Ниже мы видим, что Car A – это седан, который работает на бензине и имеет скорость 20 миль на галлон, а Car B – гибрид, который имеет 40 миль на галлон за пробег и является хэтчбеком.
Заштрихованная область, где два круга перекрываются, показывают общие черты обоих автомобилей, в том числе радио, 4 двери, возможность Bluetooth и подушки безопасности.
Диаграмма Венна наглядно показывает сходства и различия между двумя автомобилями, чтобы помочь решить, какой из них купить.
Диаграммы Эйлера-Венна
Что такое диаграммы Эйлера-Венна
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
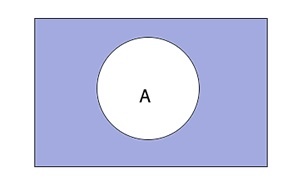
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
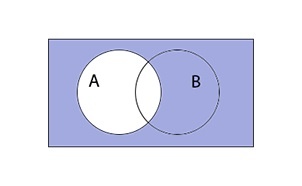
Дополнение множества
При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:
Таким образом выглядит дополнение \(\overline A\) графически:
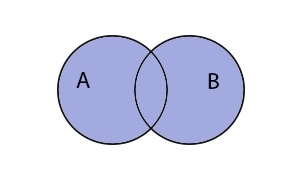
Объединение множеств
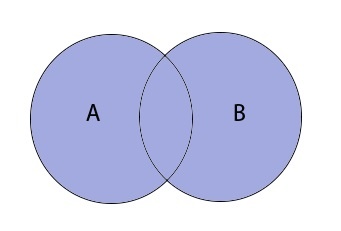
Объединение записывается следующим образом:
Таким образом объединение множеств выглядит графически:
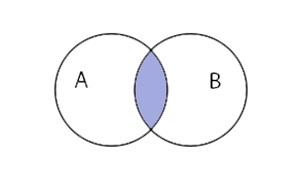
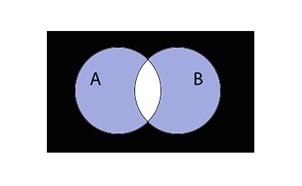
Пересечение множеств
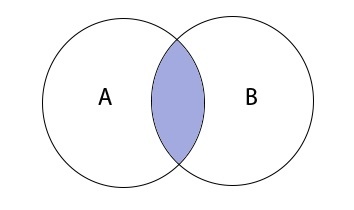
Пересечение множеств записывается следующим образом:
Таким образом пересечение множеств выглядит графически:
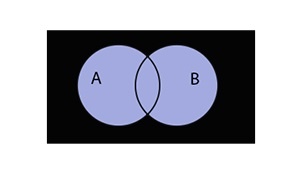
Симметричная разность множеств
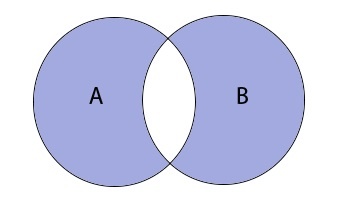
Симметричная разность A \ B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
\(A\bigtriangleup B=(A\backslash B)\cup(B\backslash A)\)
Таким образом разность выглядит графически:
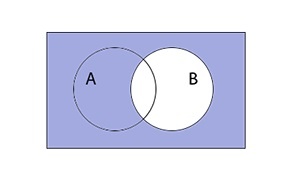
Разность множеств
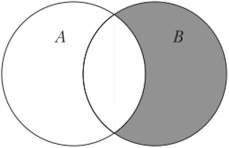
Разностью A \ B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств \(A\;\wedge\;B\)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Задача
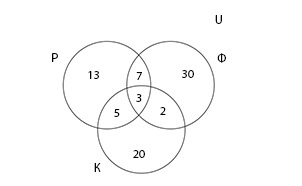
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
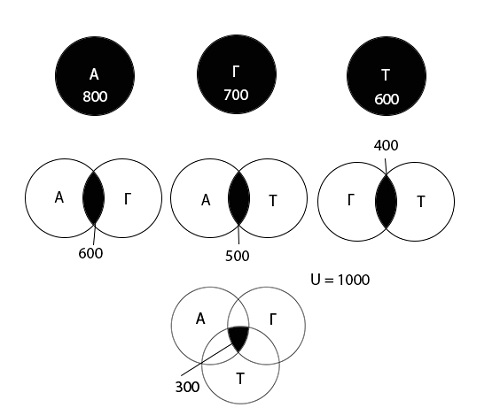
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
Теперь используя диаграмму, обозначим область, которую необходимо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
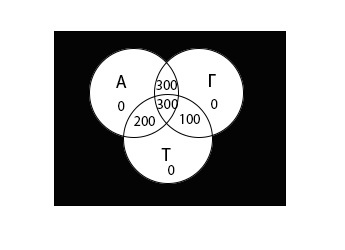
Теперь внесем значения всех областей в диаграмму:
\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)
Ответ: 100 школьников не решило ни одной задачи.
ДИАГРАММЫ ВЕННА
Полезное
Смотреть что такое «ДИАГРАММЫ ВЕННА» в других словарях:
Диаграммы Венна — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия
диаграммы венна — геометрическое наглядное представление отношений между классами (объемами понятий) в булевой алгебре с помощью кругов или иных фигур. Д. В. были введены в логику в конце XIX в. англ. логиком Дж. Венном. Элемент 1 булевой алгебры представляется… … Словарь терминов логики
Венна диаграммы — [Venn diagrams] способ графического изображения множеств. Конечное множество может быть условно представлено как совокупность точек, окруженных подходящей фигурой, например, кругом, квадратом или треугольником. Таким образом могут быть… … Экономико-математический словарь
Венна диаграммы — Способ графического изображения множеств. Конечное множество может быть условно представлено как совокупность точек, окруженных подходящей фигурой, например, кругом, квадратом или треугольником. Таким образом могут быть проиллюстрированы… … Справочник технического переводчика
ВЕННА ДИАГРАММЫ — геометрич. (точнее – топологич.) иллюстрация отношений между классами (объемами понятий) с помощью системы взаимно пересекающихся кругов (или др. контуров), введенная в конце 19 в. англ. логиком Дж. Венном (J. Venn). Лит.: Wenn J., Symbolic logic … Философская энциклопедия
ВЕННА ДИАГРАММА — графический способ изображения формул математич. логики, прежде всего формул исчисления высказываний. В. д. ппеременных классич. логики высказываний представляет собой такой набор замкнутых контуров (го меоморфных окружностям), к рый разбивает… … Математическая энциклопедия
Диаграммы Эйлера—Венна — Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. Круги Эйлера[1] геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… … Википедия
Логические диаграммы — графический (геометрический, точнее топологический) аппарат математической логики (См. Логика). Идея Л. д. была известна ещё в средние века, развивалась затем Г. В. Лейбницем, но впервые достаточно подробно и обоснованно была изложена Л.… … Большая советская энциклопедия
Диаграмма Венна — Диаграмма Венна, показывающая все пересечения греческого, русского и латинского алфавитов (буквы заглавные) Диаграмма Венна … Википедия
Венн, Джон — Джон Венн John Venn Джон Венн Дата рождения … Википедия