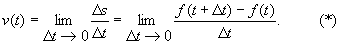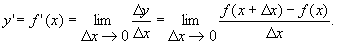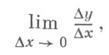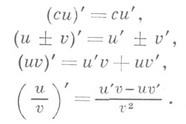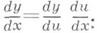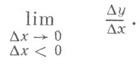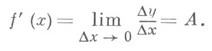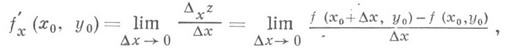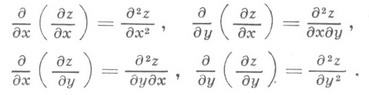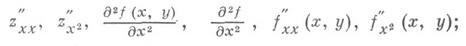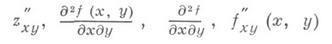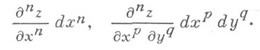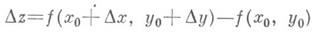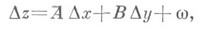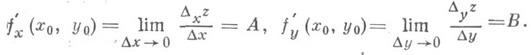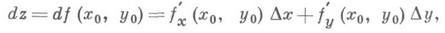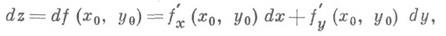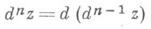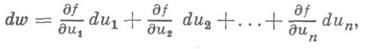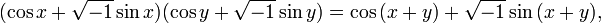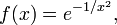Что такое дифференциальное исчисление

Дифференциальное исчисление

Полезное

Смотреть что такое «Дифференциальное исчисление» в других словарях:

Дифференциальное исчисление — Дифференциальное исчисление раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Содержание 1 Дифференциальное исчисление функций одной переменной … Википедия

Дифференциальное исчисление — Дифференциальное исчисление. Проведение касательной к графику функции y=f(x) в точке M. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ, раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной… … Иллюстрированный энциклопедический словарь

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — математическая наука, занимающаяся изучением дифференциалов функций, т. е. выражений, показывающих, в какой зависимости переменные величины находятся друг от друга. Дифференциалом функции назыв. бесконечно малое приращение, получаемое ею,… … Словарь иностранных слов русского языка

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ, см. ИСЧИСЛЕНИЕ … Научно-технический энциклопедический словарь

дифференциальное исчисление — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN differential calculus … Справочник технического переводчика

дифференциальное исчисление — раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции у = f(х) называется предел отношения приращения Δу = у1 – у0 функции к приращению Δх = x1 – х0 аргумента при Δх … Энциклопедический словарь

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — на аналитических пространствах обобщение классич. исчисления дифференциальных форм и дифференциальных операторов на случай аналитич. ространств. Об исчислении дифференциальных форм на комплексных многообразиях см. Дифференциальная форма. Пусть… … Математическая энциклопедия

Дифференциальное исчисление — Исчисление бесконечно малых, включающее так называемое Д. исчисление, а также ему обратное интегральное, принадлежит к числу наиболее плодотворных открытий человеческого ума и составило эпоху в истории точных наук. Ближайшим поводом к изобретению … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Дифференциальное исчисление

Из Википедии — свободной энциклопедии

Дифференциальное исчисление — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Формирование дифференциального исчисления связано с именами Исаака Ньютона и Готфрида Лейбница. Именно они чётко сформировали основные положения и указали на взаимообратный характер дифференцирования и интегрирования. Создание дифференциального исчисления (вместе с интегральным) открыло новую эпоху в развитии математики. С этим связаны такие дисциплины как теория рядов, теория дифференциальных уравнений и многие другие. Методы математического анализа нашли применение во всех разделах математики. Очень распространилась область применения математики в естественных науках и технике.

Дифференциальное исчисление базируется на таких важнейших понятиях математики, определение и исследование которых и составляют предмет введения в математического анализа: действительные числа (числовая прямая), функция, граница, непрерывность. Все эти понятия получили современную трактовку в ходе развития и обоснования дифференциального и интегрального исчислений.

Основная идея дифференциального исчисления состоит в изучении функции в малом. Точнее дифференциальное исчисление дает аппарат для исследования функций, поведение которых в достаточно малой окрестности каждой точки близка к поведению линейной функции или многочлена. Таким аппаратом служат центральные понятия дифференциального исчисления: производная и дифференциал.

Источник

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

— раздел математики, в к-ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу математич. анализа, имеющего чрезвычайное значение для естествознания и техники. Основной предпосылкой для создания Д. и. явилось введение в математику переменных величин (Р. Декарт, R. Descartes). В общих чертах построение дифференциального и интегрального исчислений было завершено в трудах И. Ньютона (I. Newton) и Г. Лейбница (G. Leibniz) к концу 17 в., однако вопросы обоснования с помощью понятия пре-

Производная. Пусть функция y=f(x). определена в нек-рой окрестности точки х ₀,есть приращение аргумента, Dy=f(x₀+Dx)-f(x₀).— соответствующее приращение функции. Если существует (конечный или бесконечный) предел

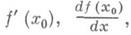
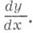
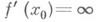
то он наз. производной функции f(x). в точке х ₀ и обозначается у’, у’ _х, Итак, по определению,

в случае касательная образует с Ох прямой угол (см. рис. 2). Таким образом, производная непрерывной функции f(x)в точке х ₀ совпадает с угловым коэффициентом tga касательной к кривой, заданной уравнением у=f(x), в ее точке с абсциссой х ₀.

Механичес кое истолков а ние производной. Пусть точка Мдвижется прямолинейно по закону s=f(t). За время Dt точка Мсместится на Ds=f(t+Dt)-f(t). Отношение Ds/Dt представляет собой среднюю скорость u _ср точки за время Dt. При неравномерном движении u_cp не постоянна. Мгновенной скоростью в момент tназ. предел средней скорости при т. е. u=f’(t). (в предположении, что эта производная существует).

Таким образом, понятие производной доставляет общее решение задачи о построении касательной к плоской кривой и задачи о вычислении скорости прямолинейного движения. Эти две задачи явились основными предпосылками в формировании понятия производной.

Функция, имеющая в точке х ₀ конечную производную, непрерывна в этой точке. В случае бесконечной производной этого может не быть. Непрерывная функция может не иметь ни конечной, ни бесконечной производной. Существуют непрерывные функции, не имеющие производной ни в одной точке области определения. Для производных основных элементарных функций справедливы следующие формулы (в любой точке области определения; исключения оговариваются):

Имеют место также следующие правила дифференцирования;

1) Если функции и(х)и u(х)дифференцируемы в точке х ₀, то функции

также дифференцируемы в этой точке, причем

2) Теорема о производной сложной функции: если функция y=f(u)дифференцируема в точке и ₀, а функция j(х)дифференцируема в точке х ₀, причем u₀=j(x_o), то сложная функция y-f(j(x))дифференцируема в точке х ₀ и y’_x=f(u₀)j'(x₀) или, в другой записи,

3) Теорема о производной обратнойфункции: если y=f(x)и x=g(y)- две взаимно обратные возрастающие (или убывающие) функции, заданные на нек-рых интервалах, и существует конечная производная то в точке y₀=f(z₀ )существует конечная производная или, в другой записи, Эта теорема допускает обобщение: если, при выполнении прочих условий, f’ (x₀) =0(f’ ( х _о)=), то g’( у _о)= (соответственно g’( у ₀)=0).

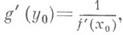
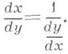
Односторонние производные. Если в точке х ₀ существует предел

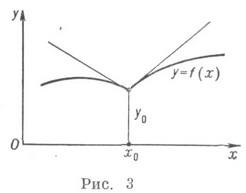
Функция f(x)имеет производную в точке х ₀ в том и только в том случае, если в этой точке существуют равные между собой правая и левая производные. Для непрерывной функции существование в точке правой (соответственно левой) производной равносильно существованию в соответствующей точке ее графика правой (соответственно левой) односторонней полукасательной с угловым коэффициентом, равным значению этой односторонней производной. Точки, в к-рых полукасательные не образуют одну прямую, называются угловыми точками (см. рис. 3).

Функция y=f(x)имеет в точке хдифференциал в том и только в том случае, если она имеет в этой точке конечную производную

Функция, для к-рой существует дифференциал, наз. дифференцируемой в рассматриваемой точке. Таким образом, дифференцируем ость функции означает одновременно и существование дифференциала, и существование конечной производной. При этом dy = df(x)=f’(x)Ax. Для независимого переменного хполагают dx= Ax и поэтому можно писать dy = f(x)dx, т. е. производная равна отношению дифференциалов:

См. также Дифференциал.

Повторный дифференциал от dy имеет вид 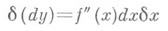и вторым дифференциалом является значение d (dy )при dx=dx.

продолжение Дифференциальное исчесление.

Д. и. функций многих переменных. Для простоты рассматривается случай функций двух переменных (за нек-рым исключением), хотя все понятия легко распространяются на случай трех и большего числа переменных. Пусть функция z=f(x, у )задана в нек-рой окрестности точки ( х ₀, у ₀ )и пусть зафиксировано значение y=y₀. Тогда f(x, y₀ )есть функция только от х. Если она имеет в х ₀ производную по х, то эта производная наз. частной производной функции f( х, у) по х в точке ( х ₀, у ₀ )и обозначается f’x( х ₀, у ₀)>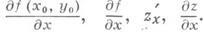Итак, по определению,

где D_xz=f(x₀+Dx, y₀)-f(x₀, y₀) — частное приращение функции по х(dz/dx в общем случае нельзя рассматривать как дробь; д/дх есть символ операции).

Аналогично определяется частная производная по у:

(где, как и в случае одного переменного, dx=Dx, dy=Dyозначают приращения независимых переменных).

Первые частные производные =f’_x( х, у) и =f’_y(x, у), или частные производные первого порядка, являясь функциями от x и у, могут в свою очередь иметь частные производные по хи у, к-рые называются, по отношению к функции z=f(x, у), частными производными второго порядка, или вторыми частными производными. При этом полагают

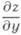
Вместо d 2 z/dx 2 употребляют также обозначения

вместо д 2 z/дхду— обозначения

Каждой частной производной отвечает нек-рый частный дифференциал, получаемый умножением ее на дифференциалы независимых переменных, взятые в степенях, равных числу дифференцирований по соответствующему переменному. Так получаются п-е частные дифференциалы, или частные дифференциалы n-го порядка:

Справедлива следующая важная теорема о смешанных производных: если в нек-рой окрестности точки ( х ₀, у ₀ )функция z=f(x, у )имеет смешанные частные производные f»_xy(x, у )и f»_yx(x, у )и эти производные непрерывны в точке ( х ₀, у ₀), то f»_xy ( х ₀, у ₀) = f»_yx( х ₀, у ₀).

Функция z=f(x, у )наз. дифференцируемой в точке ( х ₀, у ₀ )по совокупности переменных х и у, если она определена в нек-рой окрестности этой точки и ее полное приращение

может быть представлено в виде

где Аи В— некоторые числа, w/r->0 при r= 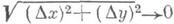(при условии, что точка (x₀+ D х, у ₀+Dу)принадлежит упомянутой окрестности). При этом выражение

наз. полным дифференциалом (первого порядка) функции f(x, у )в точке ( х ₀, у ₀);это есть главная линейная часть приращения. Функция, дифференцируемая в точке, непрерывна в этой точке (обратное не всегда верно!). Более того, дифференцируемость влечет существование конечных частных производных

Таким образом, для функции, дифференцируемой ( х ₀, у ₀).

если, подобно случаю одного переменного, положим для независимых переменных dx=Dx, dy=Dy.

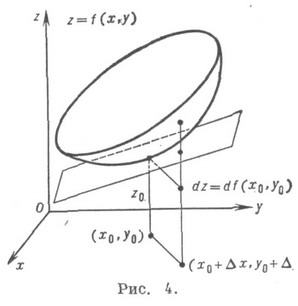
Существование конечных частных производных общем случае не влечет ее дифференцируемоcти (здесь нарушается аналогия с функциями одного переменного). Достаточный признак дифференцируемости функции двух переменных: если в нек-рой окрестности точки ( х ₀, у ₀ )функция f(x, у )имеет конечные частные производные f_x(x, у )и f’_y(x, y), непрерывные в точке ( х ₀, у ₀), то f дифференцируема в этой точке. Геометрически полный дифференциал df(x₀, y₀ )есть приращение аппликаты касательной плоскости к поверхности z=f(x,y )в точке (х ₀, у ₀, z₀), где z₀=f( х ₀, у ₀ )(см. рис. 4).

Полные дифференциалы высших порядков, подобно случаю функций одного переменного, вводятся по индукции равенством

в предположении, что дифференциал d n-1 z определе в нек-рой окрестности рассматриваемой точки и что приращения аргументов dx, dy берутся одни и те же на всех шагах. Аналогично определяются и повторные дифференциалы.

Тогда справедливы следующие теоремы:

Д. и. применяется к изучению свойств функций многих переменных: к отысканию экстремумов, к исследованию функций, задаваемых одним или несколькими неявными уравнениями, к теории поверхностей и т. д. Одним из главных инструментов при этом является Тейлора формула.

Понятия производной и дифференциала и их простейшие свойства, связанные с арифметич. действиями над функциями и суперпозицией функций, включая свойство инвариантности первого дифференциала, почти без изменений распространяются на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе понятия производной и дифференциала распространяются на функции точки абстрактного пространства.

Источник

Дифференциальное и интегральное исчисление

Математи́ческий ана́лиз — совокупность разделов математики, посвященных исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление.

В учебном процессе к анализу относят

При этом элементы функционального анализа и теории интеграла Лебега даются факультативно, а ТФКП, вариационное исчисление, теория дифференциальных уравнений читаются отдельными курсами. Строгость изложения следует образцам конца XIX века и в частности использует наивную теорию множеств.

Содержание

Исторический очерк

Предшественниками математического анализа были античный метод исчерпывания и метод неделимых. Все три направления, включая анализ, роднит общая исходная идея: разложение на бесконечно малые элементы, природа которых, впрочем, представлялась авторам идеи довольно туманно. Алгебраический подход (исчисление бесконечно малых) начинает появляться у Валлиса, Джеймса Грегори и Барроу. В полной мере новое исчисление как систему создал Ньютон, который, однако, долгое время не публиковал свои открытия. [2]

Лейбниц и его ученики

Эти определения поясняются геометрически, при этом на рис. бесконечно малые приращения изображены конечными. Рассмотрение опирается на два требования (аксиомы). Первое:

Требуется, чтобы две величины, отличающиеся друг от друга лишь на бесконечно малую величину, можно было брать [при упрощении выражений?] безразлично одну вместо другой. [7]

и проч. правила дифференцирования. Второе требование гласит:

Требуется, чтобы можно было рассматривать кривую линию как совокупность бесконечного множества бесконечно малых прямых линий. [8]

,

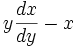
достигающее экстремальных значений в точках перегиба кривой, отношению же dy к dx не придается никакого особого значения.

Но всякая непрерывно возрастающая или убывающая величина не может превратиться из положительной в отрицательную, не проходя через бесконечность или нуль… Отсюда следует, что дифференциал наибольшей и наименьшей величины должен равняться нулю или бесконечности. [10]

Эйлер

Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этой переменного количества и чисел или постоянных количеств. [16]

Подчеркивая, что «основное различие функций лежит в способе составления их из переменного и постоянных», Эйлер перечисляет действия, «посредством которых количества могут друг с другом сочетаться и перемешиваться; действиями этими являются: сложение и вычитание, умножение и деление, возведение в степень и извлечение корней; сюда же следует отнести также решение [алгебраических] уравнений. Кроме этих действий, называемых алгебраическими, существует много других, трансцендентных, как-то: показательные, логарифмические и бесчисленные другие, доставляемые интегральным исчислением». [17] Такая трактовка позволяла без труда обращаться с многозначными функциями и не требовала пояснения, над каким полем рассматривается функция: выражение для счета определено для комплексных значений переменных даже тогда, когда для рассматриваемой задачи это не нужно.

,

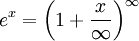
в котором лишь поздние авторы видели предельный переход. С аналитическими выражениями производились разнообразные преобразования, позволившие Эйлеру найти представления для элементарных функций в виде рядов, бесконечных произведений и т. д. Эйлер преобразует выражения для счета так, как это делают в алгебре, не обращая внимания на возможность вычислить значение функции в точке по каждой из написанных формул.

Сам ход доказательства прекрасно демонстрирует технику использования бесконечно большого. Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее:

,

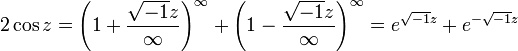
отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

.

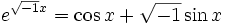
Указав различные выражения для функций, которые теперь называют элементарными, Эйлер переходит к рассмотрению кривых на плоскости, начертанным свободным движением руки. По его мнению, не для всякой такой кривой можно отыскать единое аналитическое выражение (см. также Спор о струне). [20] В XIX веке с подачи Казорати [21] это утверждение считалось ошибочным: по теореме Вейерштрасса всякая непрерывная в современном смысле кривая может быть приближенно описана полиномами. На самом деле Эйлера это едва ли убедило, ведь нужно еще переписать предельный переход при помощи символа .

В трехтомном интегральном исчислении Эйлер трактует вводит понятие интеграла так:

Лагранж

Следующим крупным произведением, сыгравшим значительную роль в развитии концепции анализа, явилась Теория аналитических функций [23] Лагранжа и обширный пересказ работ Лагранжа, выполненный Лакруа [24] в несколько эклектической манере.

,

,

и т. д. [25]

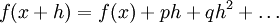
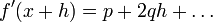
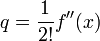
Такой подход к трактовке понятия производной используется в современной алгебре и послужил основой для создания теории аналитических функций Вейерштрасса.

Лагранж оперировал такими рядами как формальными и получил ряд замечательных теорем. В частности, впервые и вполне строго доказал разрешимость начальной задачи для обыкновенных дифференциальных уравнений в формальных степенных рядах. [26]

Вопрос об оценке точности приближений, доставляемых частными суммами ряда Тейлора, впервые был поставлен именно Лагранжем: в конце Теории аналитических функций он вывел то, что теперь называют формулой Тейлора с остаточным членом в форме Лагранжа. [27] Однако, в противоположность современным авторам, Лагранж не видел нужды в употреблении этого результата для обоснования сходимости ряда Тейлора.

Вопрос о том, действительно ли функции, употребимые в анализе, могут быть разложены в степенной ряд, в последствие стал предметом дискуссии. Конечно, Лагранжу было известно, что в некоторых точках элементарные функции могут не разлагаться в степенной ряд, однако в этих точка они и недифференцируемы ни в каком смысле. Коши в своём Алгебраическом анализе привел в качестве контрпримера функцию

.

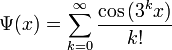
Дальнейшее развитие

В XIX веке Коши первым дал анализу твердое логическое обоснование, введя понятие последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.

В последней трети XIX века Вейерштрасс произвёл арифметизацию анализа, полагая геометрическое обоснование неудобным, и предложил определение предела через ε-δ-язык;. Тогда математики стали сомневаться в существовании множества вещественных чисел. Дедекинд ввёл вещественные числа с помощью дедекиндовых сечений. В это время попытки усовершенствования теоремы об интегрируемости по Риману привели к созданию классификации разрывности вещественных функций. Также были открыты «патологические» примеры (нигде не дифференцируемые непрерывные функции, заполняющие пространство кривые). В связи с этим Жордан разработал теорию меры, а Кантор — теорию множеств, и в начале XX века математический анализ был формализован с их помощью.

Источник