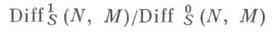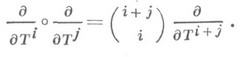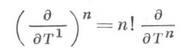Что такое дифференциальный оператор

Вычислим \(LMy:\) \[My = \left( <2D + 3>\right)y = 2y’ + 3y.\] Получаем следующее дифференциальное выражение: \[ \right) > = <\left( <+ 1> \right)\left( <2y' + 3y>\right) > = <2y''' + 3y'' + 2y' + 3y >= <\left( <2+ 3 + 2D + 3> \right)y.> \] Теперь вычислим \(MLy:\) \[Ly = \left( <+ 1> \right)y = y» + y.\] Следовательно, \[ \right) > = <\left( <2D + 3>\right)\left( \right) > = <2y''' + 3y'' + 2y' + 3y >= <\left( <2+ 3 + 2D + 3> \right)y.> \] Видно, что в данном случае коммутативный закон умножения выполняется (это справедливо для любых операторов \(L\left( D \right)\) с постоянными коэффициентами).

Источник

ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР

из совпадений их k-струй в точке рследует совпадение lf и gв той же точке; наименьшее из чисел А, удовлетворяющих этому условию для всех наз. порядком дифференциального выражения и порядком Д. о., определенного этим выражением.

На многообразии Мбез края Д. о. часто является расширением оператора, естественно определяемого фиксированным дифференциальным выражением на нек-ром (открытом в подходящей топологии) множестве бесконечно (или достаточно много раз) дифференцируемых сечений данного векторного расслоения x с базой Ми, таким образом, допускает естественное обобщение на случай пучков ростков сечений дифференцируемых расслоений. На многообразии Мс краем дМ Д. о. Lчасто определяется как расширение аналогичного оператора, естественно определенного дифференциальным выражением на множестве тех дифференцируемых функций (или сечений расслоения), ограничения к-рых на дМ лежат в ядре нек-рого Д. о. lна дМ (или удовлетворяет каким-либо др. условиям, определяемым теми или иными требованиями к. области значений оператора lна ограничениях функций из области определения оператора L, напр., неравенствами); Д. о. lназ. определяющим граничные условия для Д. о. L. Линейные Д. о. в пространствах, сопряженных к пространствам функций (или сечений), определяются как операторы, сопряженные к Д. о. указанного выше вида в этих пространствах.

3) Предыдущие примеры могут быть перенесены на случай комплексного поля, локально компактного вполне несвязного поля и (по крайней мере в случав линейных Д. о.) даже в более общую ситуацию, см. Дифференциальная алгебра.

4) Системы дифференциальных выражений определяют Д. о. в пространствах вектор-функций. Напр., Д. о. Коши-Римана, определенный дифференциальным выражением преобразует пространство пар гармонических функций на плоскости в себя.

В определении Д. о. и его обобщений (кроме обычных производных) часто используются не только обобщенные производные (естественно возникающие при рассмотрении расширений Д. о., заданных на дифференцируемых функциях) и слабые производные (связанные с переходом к сопряженному оператору), но и производные дробного и отрицательного порядков. Более того, само дифференцирование заменяется преобразованием Фурье (или другим интегральным преобразованием), применяемым к области определения и значения такого обобщенного Д. о. (см. Псевдодифференциальный оператор )так, чтобы получить возможно более простое представление соответствующей Д. в. функции Fи достичь разумной общности постановки задач и хороших свойств рассматриваемых объектов, а также построить функциональное или операционное исчисление (продолжающее соответствие между оператором дифференцирования и оператором умножения на независимую переменную, осуществляемое преобразованием Фурье).

Таким образом, теория Д. о. позволяет разрешить ряд трудностей классич. теории дифференциальных Уравнений. Использование различных расширений обычных Д. о. приводит к понятию обобщенного решения соответствующего дифференциального уравнения (к-рое в ряде случаев, связанных, напр., с эллиптич. задачами, оказывается необходимо классическим), а использование линейной структуры позволяет вводить понятие слабых решений дифференциальных уравнений. При выборе подходящего расширения Д. о., определенного дифференциальным выражением, важную роль играют связанные с конкретным видом последнего априорные оценки для решений, к-рые позволяют указать такие функциональные пространства, что в этих пространствах Д. о. непрерывен или ограничен.

Но теория Д. о. дает возможность поставить и решить и ряд принципиально новых задач по сравнению с классич. задачами теории дифференциальных уравнений. Так, для нелинейных операторов представляют интерес изучение структуры множества его неподвижных точек и действие оператора в их окрестности, а также классификация этих особых точек и вопрос об устойчивости типа особой точки при возмущении данного Д. о.; для линейных Д. о., кроме указанных выше задач, представляют интерес задачи об описании и изучении спектра Д. о., построения его резольвенты, вычислений индекса, описание структуры инвариантных подпространств данного Д. о., построение связанного с данным Д. о. гармонич. анализа (в частности, разложения по собственным функциям, что требует предварительного изучения вопросов, полноты системы собственных и присоединенных функций), изучения линейных и нелинейных возмущений данного Д. о. Эти задачи представляют особый интерес для эллиптич. Д. о., порожденных симметричными дифференциальными выражениями, в связи с теорией самосопряженных операторов в гильбертовом пространстве (в частности, со спектральной теоремой для таких операторов и теорией расширений симметрич. операторов). Теория ряда задач гиперболических и параболических (не обязательно линейных) Д. о. связана с теорией групп и полугрупп преобразований локально выпуклых пространств.

Лит.:[1] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [2] Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [3] Xёрмандер Л., Линейные дифференциальные операторы о частными производными, пер. с англ., М., 1965; [4]Бурбаки Н., Дифференцируемые и аналитические многообразия. Сводка результатов, пер. сфранц., М., 1975; [5] Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977; [6] Пале Р., Семинар по теореме Атьи-Зингера об индексе, пер. с англ., М., 1970; [7] Рейссиг Р., Сансоне Г., Конти Р., Качественная теория нелинейных дифференциальных уравнений, пер. с нем., М., 1974; [8] Фиников С. П., Метод внешних форм Картана в дифференциальной геометрии, М.- Л., 1948; [9] Скрыпник И. В., Нелинейные эллиптические уравнения высшего порядка, К., 1973; [10] Гельфанд И. М., Минлос Р. А., Шапиро 3. Я., Представления группы вращений и группы Лоренца, их применения, М., 1958; [11] Схоутен Я.-А., Тензорный анализ для физиков, пер. с англ., М., 1965; [12] Лионе Ж. П., Некоторые методы решения нелинейных краевых задач, пер. с франц., М., 1972; [13] Рождественский Б. Л., Яненко Н. Н., Системы квазилинейных уравнений и их приложения к газовой динамике, М., 1968.

М. И. Войцеховский, А. И. Штерн.

является Д. о. порядка При этом Д. о. порядка 0 наз. гомоморфизм R-модулей Множество всех таких Д. о. образует подмодуль R-модуля всех гомоморфизмов S-модулей Hom_S(N, М). В частности,

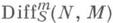
изоморфен модулю S-дифференцирований Der_S(R, М)кольца Л со значениями в М. Объединение Diff_S (M)возрастающего семейства подмодулей

является фильтрованным ассоциативным кольцом относительно операции композиции отображений. Это кольцо наз. кольцом дифференциальных операторов R-модуля Мнад подкольцом S, а соответствующее градуированное кольцо

наз. кольцом символов. Образ Д. о. D( М, М )в кольце наз. символом Д. о.

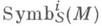
Если Л является алгеброй над полем рациональных чисел и модуль дифференциалов проективен, то существует изоморфизм S-алгебры Diff_S(R) и обертывающей алгебры алгебры Ли S-дифференцирований Der_S(R, R). В этом случае кольцо Symb_SW изоморфно симметрич. алгебре Л-модуля Der(R, R).

Напр., пусть R = k[T]- кольцо многочленов над полем k;отображения д/дТ i :определяемые формулой

(формула Тейлора), что в случае, когда характеристика поля kравна 0, дает

Если Spec (R) является аффинной групповой S- схемой, то можно рассматривать также инвариантные Д. о. кольца R(см. [2]).

Полезное

Смотреть что такое «ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР» в других словарях:

Дифференциальный оператор — Дифференциальный оператор (вообще говоря, не непрерывный, не ограниченный и не линейный) оператор, определённый некоторым дифференциальным выражением и действующий в пространствах (вообще говоря, векторнозначных) функций (или сечений… … Википедия

дифференциальный оператор — diferencialinis operatorius statusas T sritis fizika atitikmenys: angl. differential operator vok. Differentialoperator, m rus. дифференциальный оператор, m pranc. opérateur différentiel, m … Fizikos terminų žodynas

ЛИНЕЙНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР — в узком смысле оператор, действующий на функции, заданные на открытом множестве и принимающий значения в поле или по формуле где функции со значениями в том же поле, наз. коэффициентами А. Если коэффициенты принимают значения во множестве матриц… … Математическая энциклопедия

Оператор Д’Аламбера — (оператор Даламбера, волновой оператор, даламбертиан) дифференциальный оператор второго порядка где оператор Лапласа, постоянная. Иногда оператор пишется с противоположным знаком. Имеет в декартовых координатах вид … Википедия

Оператор Даламбера — Оператор Д’Аламбера (оператор Даламбера, волновой оператор, даламбертиан) дифференциальный оператор второго порядка где Δ оператор Лапласа, c постоянная. Иногда оператор пишется с противоположным знаком. Имеет в декартовых координатах вид:… … Википедия

Оператор Лапласа-Бельтрами — (называется иногда оператором Бельтрами Лапласа или просто оператором Бельтрами) дифференциальный оператор второго порядка, действующий в пространстве гладких (или аналитических) функций на римановом многообразии M. В координатах где n = dimM,… … Википедия

Оператор набла — (оператор Гамильтона) векторный дифференциальный оператор, обозначаемый символом (набла) (в Юникоде U+2207, ∇). Для трёхмерного евклидова пространства в прямоугольных декартовых координатах[1] оператор набла определяется следующим образом … Википедия

Оператор (математика) — У этого термина существуют и другие значения, см. Оператор. Оператор (позднелат. operator работник, исполнитель, от operor работаю, действую) то же, что отображение в математике. Термин оператор встречается в разных… … Википедия

Источник

СОДЕРЖАНИЕ

Определение

Обозначения

При взятии производных более высокого порядка n оператор может быть записан:

Производная функции f от аргумента x иногда задается одним из следующих способов:

В n переменных оператор однородности имеет вид

В письменной форме, следуя общепринятому математическому соглашению, аргумент дифференциального оператора обычно помещается справа от самого оператора. Иногда используется альтернативное обозначение: результат применения оператора к функции в левой части оператора и в правой части оператора, а также разница, полученная при применении дифференциального оператора к функциям с обеих сторон, обозначаются стрелками:

Такое обозначение двунаправленной стрелки часто используется для описания вероятностного тока квантовой механики.

Сопутствующий оператору

Формальное сопряжение по одной переменной

Несколько переменных

Пример

Это свойство можно доказать, используя формальное сопряженное определение выше.

Этот оператор является центральным в теории Штурма – Лиувилля, в которой рассматриваются собственные функции (аналоги собственных векторов ) этого оператора.

Свойства дифференциальных операторов

Любой многочлен в D с коэффициентами функции также дифференциальный оператор. Мы также можем составлять дифференциальные операторы по правилу

Несколько переменных

Кольцо полиномиальных дифференциальных операторов

Кольцо одномерных полиномиальных дифференциальных операторов

Кольцо многомерных полиномиальных дифференциальных операторов

Координатно-независимое описание

Отношение к коммутативной алгебре

Примеры

История

Концептуальный этап написания дифференциального оператора как чего-то отдельного приписывается Луи Франсуа Антуану Арбогасту в 1800 году.

Источник

СОДЕРЖАНИЕ

Определение

Обозначения

При взятии производных более высокого порядка n оператор может быть записан:

Производная функции f от аргумента x иногда задается одним из следующих способов:

В n переменных оператор однородности имеет вид

В письменной форме, следуя общепринятому математическому соглашению, аргумент дифференциального оператора обычно помещается справа от самого оператора. Иногда используется альтернативное обозначение: результат применения оператора к функции в левой части оператора и в правой части оператора, а также разница, полученная при применении дифференциального оператора к функциям с обеих сторон, обозначаются стрелками:

Такое обозначение двунаправленной стрелки часто используется для описания вероятностного тока квантовой механики.

Сопутствующий оператору

Формальное сопряжение по одной переменной

Несколько переменных

Пример

Это свойство можно доказать, используя формальное сопряженное определение выше.

Этот оператор является центральным в теории Штурма – Лиувилля, в которой рассматриваются собственные функции (аналоги собственных векторов ) этого оператора.

Свойства дифференциальных операторов

Любой многочлен в D с коэффициентами функции также дифференциальный оператор. Мы также можем составлять дифференциальные операторы по правилу

Несколько переменных

Кольцо полиномиальных дифференциальных операторов

Кольцо одномерных полиномиальных дифференциальных операторов

Кольцо многомерных полиномиальных дифференциальных операторов

Координатно-независимое описание

Отношение к коммутативной алгебре

Примеры

История

Концептуальный этап написания дифференциального оператора как чего-то отдельного приписывается Луи Франсуа Антуану Арбогасту в 1800 году.

Источник

Дифференциальный оператор

Производная функции f от аргумента x иногда задается одним из следующих способов:

В n переменных оператор однородности имеет вид

В письменной форме, следуя общепринятому математическому соглашению, аргумент дифференциального оператора обычно помещается справа от самого оператора. Иногда используется альтернативное обозначение: результат применения оператора к функции в левой части оператора и в правой части оператора, а также разница, полученная при применении дифференциального оператора к функциям с обеих сторон, обозначаются стрелками:

Такое обозначение двунаправленной стрелки часто используется для описания вероятностного тока квантовой механики.

сопряженный этого оператора определяется как оператор Т * <\ displaystyle T ^ <*>> такой, что

Формальное сопряжение по одной переменной

Несколько переменных

Пример

Это свойство можно доказать, используя формальное сопряженное определение выше.

Этот оператор является центральным в теории Штурма – Лиувилля, в которой рассматриваются собственные функции (аналоги собственных векторов ) этого оператора.

Любой многочлен в D с коэффициентами функции также дифференциальный оператор. Мы также можем составлять дифференциальные операторы по правилу

Кольцо одномерных полиномиальных дифференциальных операторов

Кольцо многомерных полиномиальных дифференциальных операторов

Отношение к коммутативной алгебре

Концептуальный этап написания дифференциального оператора как чего-то отдельного приписывается Луи Франсуа Антуану Арбогасту в 1800 году [2].

Источник