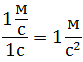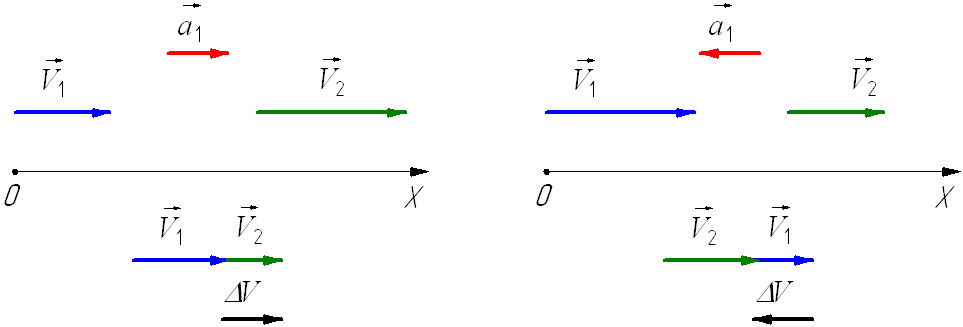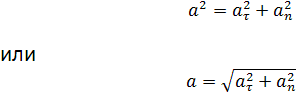Что такое динамическое ускорение
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Мгновенное ускорение
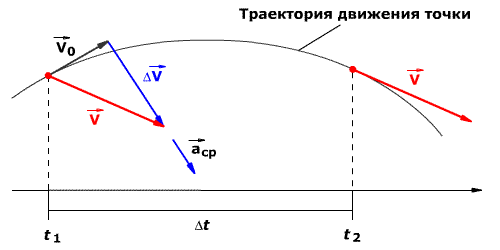
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости 
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 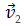Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а 
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
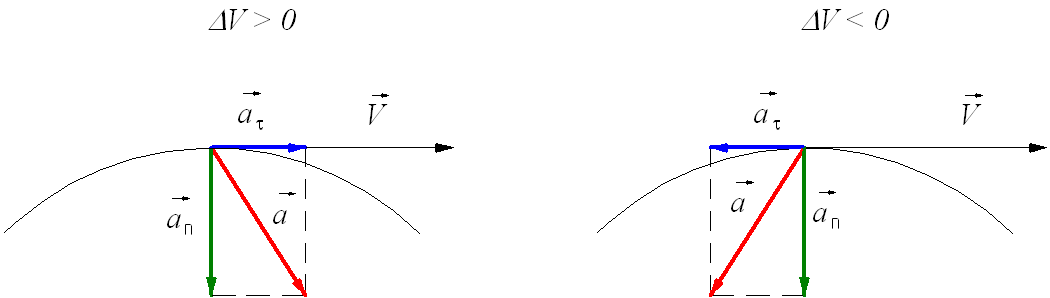
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения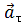 
(см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой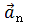 
Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Что такое динамическое ускорение
Только сегодня мы писали о том, что новые ноутбуки на процессорах Intel Core 10-го поколения Comet Lake-H не смогут стабильно работать на тактовой частоте 5 ГГц и выше. Судя по всему, их владельцев ждёт постоянный троттлинг, который не позволит им почувствовать истинный потенциал геймерских процессоров. Как оказалось, у NVIDIA есть отличное решение этой проблемы, правда для этого нужно обзавестись ноутбуком с видеокартой GeForce RTX Max-Q.
реклама
Совсем недавно AMD представила новую технологию для ноутбуков на основе собственных процессоров Renoir – SmartShift. Суть её заключается в следующем: поскольку ноутбук имеет небольшой размер, система охлаждения у процессора и видеокарты общая. В этом случае теплоотвод системы оказывается больше, чем требуется в отдельности для видеокарты или процессора в отдельности, но меньше, чем требуют они оба под нагрузкой. Если раньше обходились обычным сбросом тактовых частот процессора, то теперь в дело вступает умная технология.
Dynamic Boost от NVIDIA – это правильное распределение ресурсов между тепловым балансом системы охлаждения и производительностью. Новая программа берёт на себя заботу о контроле за тепловыделением, гарантируя, что там, где будет нужна максимальная тактовая частота процессора – она будет предоставлена. Точно такая же ситуация и с видеокартой. На самом деле прирост производительности не выходит за 10%, однако в дело вступают несколько факторов, главным из которых является универсальность.
Большинство современных устройств используют датчики для контроля и управления различными физическими величинами, такими как давление, температура, влажность, интенсивность света, направление и т.д. Один из таких датчиков, используемый для измерения ускорения устройств, называется датчиками акселерометра.
Когда-то давно вы бы нашли такие датчики только в современных машинах, таких как космические ракеты или реактивные самолеты. Теперь они есть практически в каждом смартфоне, ноутбуке, автомобиле и игровой консоли. Давайте копнем глубже и выясним, что это такое, как они работают, и для чего они используются?
Что такое акселерометр?
Измеряя величину гравитационного ускорения, инструмент может вычислить угол, под которым он наклонен относительно Земли. Например, акселерометр, установленный на поверхности Земли, будет измерять ускорение 9,81 м / с2 в прямом направлении вверх.
Измеряя величину динамического ускорения, можно определить, насколько быстро и в каком направлении движется устройство. Например, трехосевой акселерометр может определять величину и направление (во всех трех осях) ускорения как векторную величину.
Акселерометры используются в различных отраслях промышленности и научных исследованиях. Они в основном используются в электронных устройствах для определения ориентации, ускорения координат, ударов и вибрации.
Акселерометры, встроенные в смартфоны, например, выясняют, когда переключать макет экрана с ландшафтного на портретный. Данные, предоставляемые этими датчиками, могут помочь определить, идет ли устройство вверх или падает вниз.
Высокочувствительные акселерометры интегрированы в инерциальные навигационные системы ракет и реактивных двигателей. Беспилотные летательные аппараты также используют такие устройства для стабилизации полета.
Как работает акселерометр?
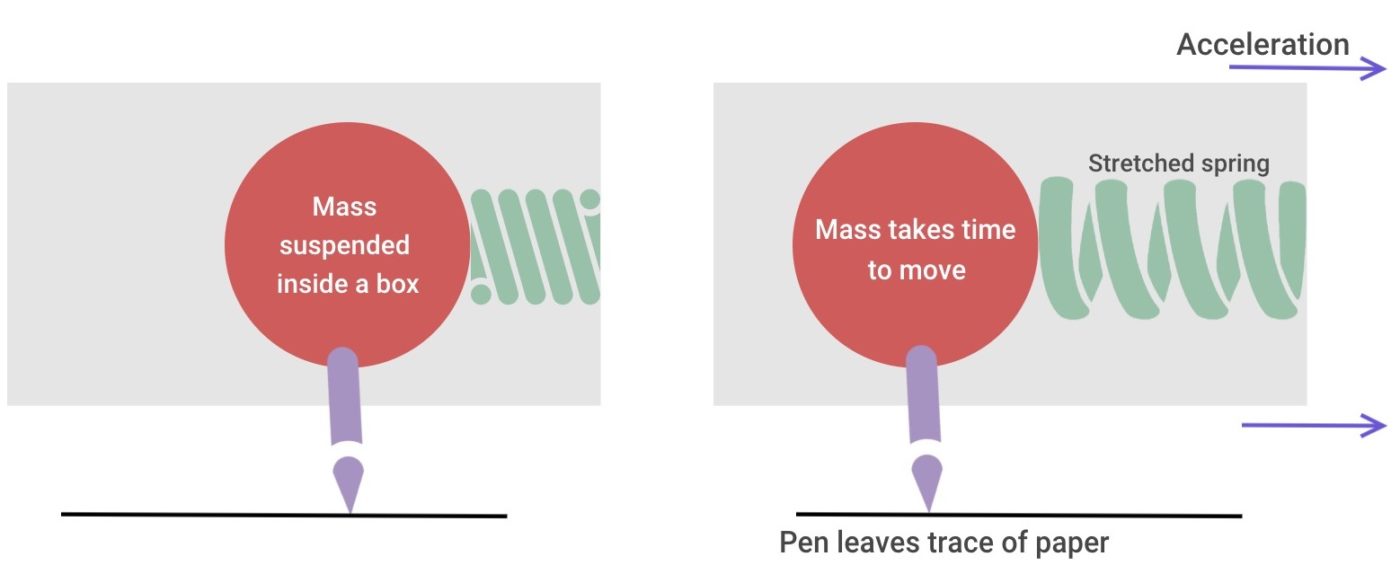
Механический акселерометр состоит из пружины, прикрепленной массой. Эта пружина обычно подвешивается внутри наружного корпуса. Когда все устройство ускоряется, корпус сразу же движется в том же направлении. Масса, однако, остается в своем положении (на короткое время), растягивая пружину с силой, соответствующей ускорению.
Принцип работы механического акселерометра
Измеряя длину пружины растяжения, мы можем определить ускорение. Это может быть сделано различными способами. Сейсмометр, например, использует тот же принцип для измерения землетрясений.
Когда происходит землетрясение, он трясет корпус сейсмометра, но масса движется дольше. К массе прикрепляется ручка, чтобы проследить ее движение на бумажном графике.
Современные акселерометры генерируют электрические или магнитные сигналы вместо того, чтобы использовать след от ручки на бумаге.
Самые распространенные типы акселерометров
Большинство коммерческих устройств оснащены емкостными, пьезорезистивными и пьезоэлектрическими приборами для преобразования механического движения в электрический сигнал.
1. Пьезоэлектрические акселерометры используют пьезоэлектрический эффект определенных материалов для измерения ускорения, вибрации или механического удара. Эти материалы накапливают электрический заряд (пьезоэлектричество) в ответ на приложенное механическое напряжение.
Принцип работы пьезоэлектрического акселерометра
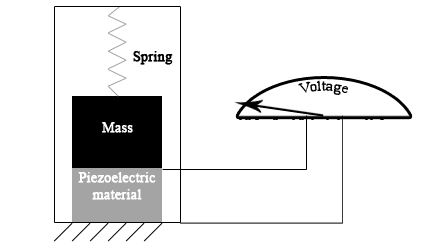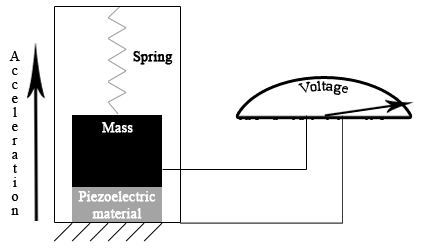
К массе прикрепляется пьезоэлектрический материал, например, цирконат-титанат свинца. При движении акселерометра масса оказывает механическое давление на этот материал. В результате этого материал вырабатывает крошечное электрическое напряжение, которое можно расшифровать, чтобы вычислить соответствующее ускорение.
2. Пьезорезистивные акселерометры работают по аналогичному принципу. Они используют изменение сопротивления пьезорезистивных материалов для преобразования механического напряжения в выходное напряжение постоянного тока. Эти типы акселерометров подходят для измерений удара, где уровень g и диапазон частот значительно высоки.
Endevco 727 | легкий пьезорезистивный акселерометр, идеально подходящий для измерения удара при испытаниях на падение
Пьезоэлектрические компоненты, напротив, не имеют себе равных по высокотемпературному диапазону и малому весу в упаковке.
3. Емкостные акселерометры основаны на изменении электрической емкости в ответ на ускорение. Они содержат два компонента: первичную (стационарную) пластину, прикрепленную к корпусу, и вторичную пластину, соединенную с массой, которая свободно перемещается внутри корпуса.
Емкость изменяется с расстоянием между двумя металлическими пластинами, и, измеряя емкость, можно определить приложенное ускорение. Эти типы акселерометров могут измерять постоянное, а также медленное переходное и периодическое ускорение.
Трехосный емкостный акселерометр
Современные акселерометры бывают всех трех форм. Они часто представляют собой микроэлектромеханические системы (MEMS), содержащие несколько компонентов, каждый размером от 1 до 100 микрометров. Акселерометры, встроенные в планшеты и смартфоны, обычно имеют площадь менее 100 миллиметров.
Микромеханический акселерометр чувствителен только к одному направлению в плоскости. Двухосевой акселерометр построен путем интеграции двух устройств перпендикулярно, а трехосный акселерометр может быть сделан путем добавления другого устройства вне плоскости. Интегрированный модуль может быть гораздо более точным, чем три отдельных устройства, объединенные после упаковки.
Для достижения сверхвысокой чувствительности можно использовать квантовое туннелирование. Однако этот процесс является чрезвычайно сложным и дорогостоящим.
С помощью существующих технологий мы можем измерять ускорения до тысяч g. Инженерам и производителям приходится идти на компромисс между максимальным измеряемым ускорением и чувствительностью устройства.
Применение
Акселерометры используются в различных областях, от инженерной и бытовой электроники до биологии и медицинских технологий. Ниже приведены наиболее часто используемые датчики акселерометров.
Навигация
Инерциальная навигационная система (также называемая инерциальной эталонной платформой) использует компьютер и акселерометры для непрерывного измерения местоположения, ориентации и скорости движущегося объекта без каких-либо внешних ориентиров.
Инженерия
Акселерометры широко используются для измерения вибрации на машинах, автомобильных двигателях и зданиях. В автомобильном секторе акселерометры с высоким значением g используются для обнаружения дорожно-транспортных происшествий и установки подушек безопасности в нужное время.
Они также используются для контроля работоспособности оборудования и регистрации вибрации вращающихся инструментов, таких как компрессоры, турбины, которые, если их не обслуживать, могут привести к дорогостоящему ремонту. Некоторые акселерометры специально настроены (встроены в гравиметры) для измерения гравитационных сил.
Бытовая электроника
Многие производители ноутбуков используют акселерометры для защиты жестких дисков от повреждений. Если датчик обнаруживает внезапное падение, головки жесткого диска припаркованы, чтобы избежать повреждения диска и потери данных.
Биология и медицинское применение
В биологических науках все чаще используются акселерометры. Данные, получаемые с помощью высокочувствительных трехосных акселерометров, позволяют ученым различать поведенческие модели животных, когда они находятся вне поля зрения.
Многие автоматические внешние дефибрилляторы содержат акселерометр для определения глубины сдавления грудной клетки СЛР.
Несколько компаний производят часы для спортсменов, которые состоят из акселерометров для измерения скорости и пройденных дистанций бегунов. Современные будильники фазы сна также интегрированы с акселерометрическими датчиками, так что они могут обнаружить движение спящего и разбудить человека в цикле не-быстрого сна.
Всё, что вы хотели знать о динамическом программировании, но боялись спросить
Я был крайне удивлён, найдя мало статей про динамическое программирование (далее просто динамика) на хабре. Мне всегда казалось, что эта парадигма довольно сильно распространена, в том числе и за пределами олимпиад по программированию. Поэтому я постараюсь закрыть этот пробел своей статьёй.
Основы
Пожалуй, лучшее описание динамики в одно предложение, которое я когда либо слышал:
Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А. Кумок.
Чтобы успешно решить задачу динамикой нужно:
1) Состояние динамики: параметр(ы), однозначно задающие подзадачу.
2) Значения начальных состояний.
3) Переходы между состояниями: формула пересчёта.
4) Порядок пересчёта.
5) Положение ответа на задачу: иногда это сумма или, например, максимум из значений нескольких состояний.
Порядок пересчёта
Существует три порядка пересчёта:
1) Прямой порядок:
Состояния последовательно пересчитывается исходя из уже посчитанных.
2) Обратный порядок:
Обновляются все состояния, зависящие от текущего состояния.
3) Ленивая динамика:
Рекурсивная мемоизированная функция пересчёта динамики. Это что-то вроде поиска в глубину по ацикличному графу состояний, где рёбра — это зависимости между ними.
Элементарный пример: числа Фибоначчи. Состояние — номер числа.
Все три варианта имеют права на жизнь. Каждый из них имеет свою область применения, хотя часто пересекающуюся с другими.
Многомерная динамика
Пример одномерной динамики приведён выше, в «порядке пересчёта», так что я сразу начну с многомерной. Она отличается от одномерной, как вы уже наверно догадались, количеством измерений, то есть количеством параметров в состоянии. Классификация по этому признаку обычно строится по схеме «один-два-много» и не особо принципиальна, на самом деле.
Многомерная динамика не сильно отличается от одномерной, в чём вы можете убедиться взглянув на пару примеров:
Пример №1: Количество СМСок
Раньше, когда у телефонов были кнопки, их клавиатуры выглядели примерно так:
Требуется подсчитать, сколько различных текстовых сообщений множно написать используя не более k нажатий на такой клавиатуре.
Прямой пересчёт:
Обратный пересчёт:
При использовании обратного пересчёта всё проще: мы всегда обращаемся вперёд, так что в отрицательные элементы мы не уйдём.
5) Ответ — это сумма всех состояний.
Пример №2: Конь
4) А теперь самое интересное в этой задаче: порядок. Здесь нельзя просто взять и пройтись по строкам или по столбцам. Потому что иначе мы будем обращаться к ещё не пересчитанным состояниям при прямом порядке, и будем брать ещё недоделанные состояния при обратном подходе.
Есть два пути:
1) Придумать хороший обход.
2) Запустить ленивую динамику, пусть сама разберётся.
Если лень думать — запускаем ленивую динамику, она отлично справится с задачей.
Если не лень, то можно придумать обход наподобие такого:
Этот порядок гарантирует обработанность всех требуемых на каждом шаге клеток при прямом обходе, и обработанность текущего состояния при обратном.
Динамика и матрица переходов
Если никогда не умножали матрицы, но хотите понять этот заголовок, то стоит прочитать хотя бы вики.
А теперь, зачем всё это надо. Умножение матриц обладает свойством ассоциативности, то есть (но при этом не обладает коммутативностью, что по-моему удивительно). Это свойство даёт нам право сделать так: .
А теперь пример посерьёзнее:
Пример №3: Пилообразная последовательность
Для начала решение без матрицы перехода:
Динамика по подотрезкам
Это класс динамики, в котором состояние — это границы подотрезка какого-нибудь массива. Суть в том, чтобы подсчитать ответы для подзадач, основывающихся на всех возможных подотрезках нашего массива. Обычно перебираются они в порядке увеличения длины, и пересчёт основывается, соответственно на более коротких отрезках.
Пример №4: Запаковка строки
Вот Развернутое условие. Я вкратце его перескажу:
Необходимо по строке s узнать длину самой короткой сжатой строки, разжимающийся в неё.
Решается эта задача, как вы уже наверняка догадались, динамикой по подотрезкам.
1) Состояние динамики: d[l][r] — сжатая строка минимальной длины, разжимающаяся в строку s[l:r]
2) Начальные состояния: все подстроки длины один можно сжать только в них самих.
3) Пересчёт динамики:
У лучшего ответа есть какая-то последняя операция сжатия: либо это просто строка из заглавных букв, или это конкатенация двух строк, или само сжатие. Так давайте переберём все варианты и выберем лучший.
Пример №5: Дубы
Динамика по поддеревьям
Параметром состояния динамики по поддеревьям обычно бывает вершина, обозначающая поддерево, в котором эта вершина — корень. Для получения значения текущего состояния обычно нужно знать результаты всех своих детей. Чаще всего реализуют лениво — просто пишут поиск в глубину из корня дерева.
Пример №6: Логическое дерево
Требуется найти минимальное количество изменений логических операций во внутренних вершинах, такое, чтобы изменилось значение в корне или сообщить, что это невозможно.
Динамика по подмножествам
В динамике по подмножествам обычно в состояние входит маска заданного множества. Перебираются чаще всего в порядке увеличения количества единиц в этой маске и пересчитываются, соответственно, из состояний, меньших по включению. Обычно используется ленивая динамика, чтобы специально не думать о порядке обхода, который иногда бывает не совсем тривиальным.
Пример №7: Гамильтонов цикл минимального веса, или задача коммивояжера
Динамика по профилю
Классическими задачами, решающимися динамикой по профилю, являются задачи на замощение поля какими-нибудь фигурами. Причём спрашиваться могут разные вещи, например, количество способов замощения или замощение минимальным количеством фигур.
Профиль — это k (зачастую один) столбцов, являющиеся границей между уже замощённой частью и ещё не замощённой. Эта граница заполнена только частично. Очень часто является частью состояния динамики.
Почти всегда состояние — это профиль и то, где этот профиль. А переход увеличивает это местоположение на один. Узнать, можно ли перейти из одного профиля в другой можно за линейное от размера профиля время. Это можно проверять каждый раз во время пересчёта, но можно и предподсчитать. Предподсчитывать будем двумерный массив can[mask][next_mask] — можно ли от одной маски перейти к другой, положив несколько фигурок, увеличив положение профиля на один. Если предподсчитывать, то времени на выполнение потребуется меньше, а памяти — больше.
Пример №8: Замощение доминошками
Здесь профиль — это один столбец. Хранить его удобно в виде двоичной маски: 0 — не замощенная клетка столбца, 1 — замощенная. То есть всего профилей .
0) Предподсчёт (опционально): перебрать все пары профилей и проверить, что из одного можно перейти в другой. В этой задаче это проверяется так:
Примеры переходов (из верхнего профиля можно перейти в нижние и только в них):
Полученная асимптотика — .
Динамика по изломанному профилю
Это очень сильная оптимизация динамики по профилю. Здесь профиль — это не только маска, но ещё и место излома. Выглядит это так:
Теперь, после добавления излома в профиль, можно переходить к следующему состоянию, добавляя всего одну фигурку, накрывающую левую клетку излома. То есть увеличением числа состояний в N раз (надо помнить, где место излома) мы сократили число переходов из одного состояния в другое с до . Асимптотика улучшилась с до .
Переходы в динамике по изломанному профилю на примере задачи про замощение доминошками (пример №8):
Восстановление ответа
Иногда бывает, что просто знать какую-то характеристику лучшего ответа недостаточно. Например, в задаче «Запаковка строки» (пример №4) мы в итоге получаем только длину самой короткой сжатой строки, но, скорее всего, нам нужна не её длина, а сама строка. В таком случае надо восстановить ответ.
В каждой задаче свой способ восстановления ответа, но самые распространенные:
Небольшие оптимизации
Память
Зачастую в динамике можно встретить задачу, в которой состояние требует быть посчитанными не очень большое количество других состояний. Например, при подсчёте чисел Фибоначчи мы используем только два последних, а к предыдущим уже никогда не обратимся. Значит, можно про них забыть, то есть не хранить в памяти. Иногда это улучшает асимптотическую оценку по памяти. Этим приёмом можно воспользоваться в примерах №1, №2, №3 (в решении без матрицы перехода), №7 и №8. Правда, этим никак не получится воспользоваться, если порядок обхода — ленивая динамика.
Время
Иногда бывает так, что можно улучшить асимптотическое время, используя какую-нибудь структуру данных. К примеру, в алгоритме Дейкстры можно воспользоваться очередью с приоритетами для изменения асимптотического времени.
Замена состояния
В решениях динамикой обязательно фигурирует состояние — параметры, однозначно задающие подзадачу, но это состояние не обязательно одно единственное. Иногда можно придумать другие параметры и получить с этого выгоду в виде снижения асимптотического времени или памяти.
Пример №9: Разложение числа
Решение №1:
Решение №2:
Строки здесь обозначают слагаемые.
Первое решение последовательно добавляет по одной строчке внизу таблицы, а второе — по одному столбцу слева таблицы. Вариантов размера следующей строчки много — главное, чтобы она была больше предыдущей, а столбцов — только два: такой же как предыдущий и на единичку больше.
Заключение
Основным источником была голова, а туда информация попала с лекций в Летней Компьютерной Школе (для школьников), а также кружка Андрея Станкевича и спецкурса Михаила Дворкина (darnley).
Спасибо за внимание, надеюсь эта статья кому-нибудь пригодится! Хотя мне уже пригодилась — оказывается, написание статьи это хороший способ всё вспомнить.