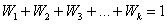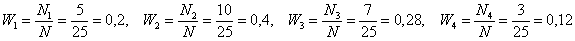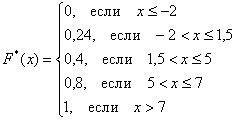Что такое дискретный ряд в статистике
Лекция 7: Показатели вариации в статистике
Признаки, изучаемые статистикой, варьируются (отличаются друг от друга) у различных единиц совокупности в один и тот же период или момент времени. Например, варьируется рост людей, их заработная плата т.п.
Причиной вариации являются разные условия существования разных единиц совокупности. Например, огромное число причин влияет на рост человека, его заработную платы и т.д.
Для управления и изучения вариации статистикой разработаны специальные методы исследования вариации, система показателей, с помощью которой вариация измеряется, характеризуются ее свойства.
Первым этапом статистического изучения вариации является построение ряда распределения (или вариационного ряда) – упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака и подсчет числа единиц с тем или иным значением признака.
Ряд распределения бывает дискретным и интервальным.
Дискретный ряд распределения – это таблица, состоящая из двух столбцов (строк) – конкретных значений варьирующего признака Xi и числа единиц совокупности с данным значением признака fi – частот; число групп в дискретном ряду определяется числом реально существующих значений варьирующего признака. В следующей таблице приведен пример дискретного ряда распределения:
| Вес студента, кг | 48 | 50 | 53 | 55 | 56 | 59 | 62 | 64 | 68 | 70 | 72 | 77 | 85 | 88 | Итого |
| Кол-во студентов, чел. | 1 | 3 | 2 | 1 | 1 | 2 | 3 | 2 | 2 | 3 | 5 | 2 | 2 | 1 | 30 |
Трансформируем дискретный ряд, представленный в таблице выше, в интервальный ряд распределения. Для этого необходимо выбрать оптимальное число групп (интервалов признака) и установить длину (размах) интервала. Поскольку при анализе ряда распределения сравнивают частоты в разных интервалах, необходимо, чтобы длина интервалов была постоянной. Если приходится иметь дело с интервальным рядом распределения с неравными интервалами, то для сопоставимости нужно частоты (f) или частости (d) привести к единице интервала, полученное значение называется плотностью ρ, то есть ρ = f/h.
Оптимальное число групп выбирается так, чтобы в достаточной мере отразилось разнообразие значений признака в совокупности и, в то же время, закономерность в распределении, а его форма не искажалась случайными колебаниями частот. Если групп будет слишком мало, то не проявится закономерность вариации, а если групп будет чрезмерно много, то случайные скачки частот исказят форму распределения.
Чаще всего число групп в ряду распределения определяют по формуле Стерждесса:
где k – число групп (округляемое до ближайшего целого числа); N – численность совокупности.
Из формулы Стерджесса видно, что число групп k – это функция объема данных (N).
Зная число групп, рассчитывают длину (размах) интервала по формуле:
где Xмax и Xmin — максимальное и минимальное значения в совокупности.
В нашем примере про вес студентов по формуле Стерждесса определим число групп: k = 1 + 3,322lg30 = 1+ 3,322*1,477 = 5,907. Так как число групп не может быть дробным, то необходимо округлить до ближайшего целого числа полученное значение 5,907. Таким образом получим k = 6.
Рассчитаем длину (размах) интервала: h = (88 – 48)/6 = 40/6 = 6,667 (кг).
Теперь построим интервальный ряд студентов по весу с 6 группами с интервалом 6,667 кг.
При изучении вариации применяются такие характеристики ряда распределения, которые описывают количественно его структуру, строение. Такова, например, медиана – величина варьирующего признака, делящая совокупность на две равные по численности части (со значением признака меньше медианы и со значением признака больше медианы).
В интервальном ряду распределения для нахождения медианы применяется формула:
fMe – частота в медианном интервале.
Правила построения дискретных и интервальных рядов распределения
Что такое группировка статистических данных, и как она связана с рядами распределения, было рассмотрено в первой части этой лекции, там же можно узнать, о том что такое дискретный и вариационный ряд распределения.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.
Как построить дискретный вариационный ряд распределения
0 1 2 3 1
2 1 2 1 0
4 3 2 1 1
1 0 1 0 2
Решение:
Вторая колонка это частота – как часто встречается наша варианта в исследуемом явление – название колонки так же берем из задания — распределения семей – значит наша частота это число семей с соответствующим количеством детей.
В итоге макет нашей таблицы будет выглядеть так:
И расставим эти данные в первой колонке нашей таблицы в логическом порядке, в данном случае возрастающем от 0 до 4. Получаем
| Число детей в семье — (х) | Количество семей (f) |
| 0 1 2 3 4 |
И в заключение подсчитаем, сколько же раз встречается каждое значение варианты.
0 1 2 3 1
2 1 2 1 0
4 3 2 1 1
1 0 1 0 2
В результате получаем законченную табличку или требуемый ряд распределения семей по количеству детей.
| Число детей в семье — (х) | Количество семей (f) |
| 0 1 2 3 4 | 4 8 5 2 1 |
| Итого | 20 |
Задание. Имеются данные о тарифных разрядах 30 рабочих предприятия. Построить дискретный вариационный ряд распределения рабочих по тарифному разряду. 2 3 2 4 4 5 5 4 6 3
1 4 4 5 5 6 4 3 2 3
4 5 4 5 5 6 6 3 3 4
Как построить интервальный вариационный ряд распределения
Построим интервальный ряд распределения, и посмотрим чем же его построение отличается от дискретного ряда.
Пример 2. Имеются данные о величине полученной прибыли 16 предприятий, млн. руб. — 23 48 57 12 118 9 16 22 27 48 56 87 45 98 88 63. Построить интервальный вариационный ряд распределения предприятий по объему прибыли, выделив 3 группы с равными интервалами.
Общий принцип построения ряда, конечно же, сохраниться, те же две колонки, те же варианта и частота, но в здесь варианта будет располагаться в интервале и подсчет частот будет вестись иначе.
Вторая колонка это частота – как часто встречается наша варианта в исследуемом явление – название колонки так же берем из задания — распределения предприятий – значит наша частота это число предприятий с соответствующей прибылью, в данном случае попадающие в интервал.
В итоге макет нашей таблицы будет выглядеть так:
где i – величина или длинна интервала,
Хmax и Xmin – максимальное и минимальное значение признака,
n – требуемое число групп по условию задачи.
Рассчитаем величину интервала для нашего примера. Для этого среди исходных данных найдем самое большое и самое маленькое
23 48 57 12 118 9 16 22 27 48 56 87 45 98 88 63 – максимальное значение 118 млн. руб., и минимальное 9 млн. руб. Проведем расчет по формуле.
В расчете получили число 36,(3) три в периоде, в таких ситуациях величину интервала нужно округлить до большего, чтобы после подсчетов не потерялось максимальное данное, именно поэтому в расчете величина интервала 36,4 млн. руб.
Обратим внимание если бы мы не округлили величину интервала до 36,4, а оставили бы ее 36,3, то последнее значение у нас бы получилось 117,9. Именно для того чтобы не было потери данных необходимо округлять величину интервала до большего значения.
При проведении обработки данных лучше всего отобранные данные обозначить условными значками или цветом, для упрощения обработки.
23 48 57 12 118 9 16 22
27 48 56 87 45 98 88 63
Первый интервал обозначим желтым цветом – и определим сколько данных попадает в интервал от 9 до 45,4, при этом данное 45,4 будет учитываться во втором интервале (при условии что оно есть в данных) – в итоге получаем 7 предприятий в первом интервале. И так дальше по всем интервалам.
По первому интервалу — 23 + 12 + 9 + 16 + 22 + 27 + 45 = 154 млн. руб.
По второму интервалу — 48 + 57 + 48 + 56 + 63 = 272 млн. руб.
По третьему интервалу — 118 + 87 + 98 + 88 = 391 млн. руб.
| Объем полученной прибыли, млн. руб. — (х) | Число предприятий (f) | Общий объем прибыли, млн. руб. |
| 9,0 — 45,4 45,4 — 81,8 81,8 — 118,2 | 7 5 4 | 154 272 391 |
| Итого | 16 | 817 |
Задание. Имеются данные о величине вклада в банке 30 вкладчиков, тыс. руб. 150, 120, 300, 650, 1500, 900, 450, 500, 380, 440,
600, 80, 150, 180, 250, 350, 90, 470, 1100, 800,
500, 520, 480, 630, 650, 670, 220, 140, 680, 320
Построить интервальный вариационный ряд распределения вкладчиков, по размеру вклада выделив 4 группы с равными интервалами. По каждой группе подсчитать общий размер вкладов.
2. Дискретный вариационный ряд.
Полигон частот и эмпирическая функция распределения
На вводном уроке по математической статистике мы узнали, что такое математическая статистика, и теперь обо всём подробнее. Далее для удобства я буду нумеровать статьи и постараюсь делать их не слишком длинными. Потому что всё действительно просто, и главное, здесь научиться рациональной технике вычислений, на которую и будет сделан особый упор.
Интервальные и дискретные вариационные ряды почти сразу же встретились в предыдущей статье, и мы начинаем с дискретного случая, когда количественная эмпирическая величина 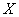
…что-то не понятно по терминам? Срочно изучать первый урок! (ссылка выше)
Дискретный вариационный ряд – это упорядоченное по возрастанию (как правило) множество вариант 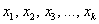
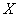
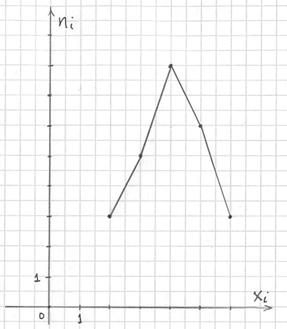
Частоты выборочной совокупности обозначают через 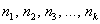
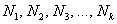
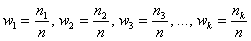
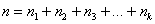
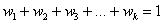
Аналогично для совокупности генеральной: 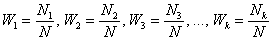
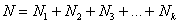
И тут вспоминается Пример 2 об оценках по матанализу в группе из 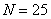
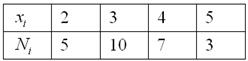
– пожалуйста, пример дискретного вариационного ряда, где варианты 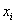
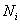
Для разминки найдём относительные частоты:
и непременно проконтролируем, что: 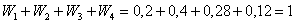
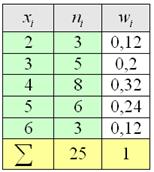
Все вычисления обычно проводят на калькуляторе либо в Экселе, а результаты заносят в таблицу, при этом, в статистике данные чаще располагают не в строках, а в столбцах: 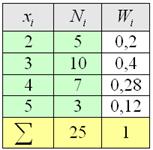
Такое расположение обусловлено тем, что количество вариант может быть достаточно велико, и они просто не вместятся в строчку. Не редкость, когда их 10-20, а бывает, и 100-200, что тоже и неоднократно встречалось в моей практике. И это не какие-то супер-пупер расчёты, а учебные задачи!
После сей позитивной новости продолжаем 🙂
Откуда берутся дискретные вариационные ряды? Такие ряды появляются в результате учёта дискретной характеристики статистической совокупности, причём, варианты ряда не отличаются большим разнообразием. Например, оценки (коих не так много) в примере выше.
И сейчас мы примем непосредственное участие в этом процессе:
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3. Требуется:
– составить вариационный ряд и построить полигон частот;
– найти относительные частоты и построить эмпирическую функцию распределения.
Чего томиться? – вся тема урока в одной задаче!
Решение: в условии прямо сказано о том, что перед нами выборка из генеральной совокупности (всех рабочих цеха), и первое, что логично сделать – подсчитать её объем, т.е. количество рабочих. В данном случае это легко сделать устно: 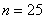
Квалификационные разряды – есть величина дискретная, и поэтому нам предстоит составить дискретный вариационный ряд (обратите внимание, что в условии ничего не сказано о характере ряда).
Если у вас под рукой нет вычислительных программ, то вручную (Эксель разберём ниже). При этом оптимальным может быть следующий алгоритм: сначала окидываем взглядом все числа и определяем среди них минимальное (примерно) и максимальное (примерно). В данном случае ориентировочный диапазон – от 1 до 7. Записываем их в столбец на черновике и обводим в кружочки. Далее начинаем вычёркивать карандашом числа из исходного списка: 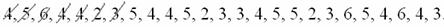
и делать около соответствующих кружков засечки:
После того, как все числа будут вычеркнуты, подсчитываем количество засечек в каждой строке: 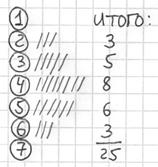
И обязательно проверяем, получается ли у нас в сумме объём выборки 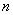
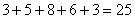

…ну что же, вполне и вполне логично – рабочих средней квалификации много, а учеников и мастеров – мало. Полученные результаты позволяют достаточно точно судить об уровне квалификации всего цеха (если, конечно, выборка представительна)
Построенный вариационный ряд также называют статистическим распределением выборки, причём, этот термин применИм не только для дискретного, но и для интервального ряда, который мы рассмотрим на следующем уроке.
Построим полигон частот. Это статистический аналог многоугольника распределения дискретной случайной величины (кто изучал). Полигон частот – это ломаная, соединяющая соседние точки 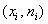
…эх, ностальгия. Но, пятилетку-другую, думается, так решать ещё будут.
Теперь современный способ:
Решаем! – исходные данные с пошаговой инструкцией прилагаются.
Вторая часть задачи. Найдём относительные частоты 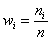
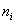

– обязательно проверяем, что сумма относительных частот равна единице!
Иногда требуется построить полигон относительных частот. Как вы правильно догадываетесь – это ломаная, соединяющая соседние точки 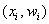
А теперь посмотрим на относительные частоты и задумаемся, на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что 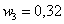
А вот если учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты 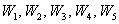
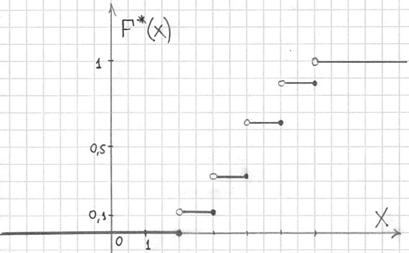
Построим эмпирическую функцию распределения 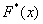
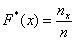
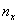
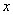
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
Очевидно, что на интервале 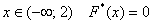
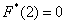
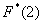
На промежутке 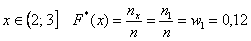
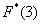
На промежутке 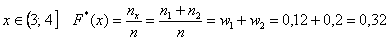
– если 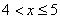

– если 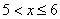
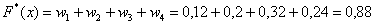
– и, наконец, если 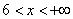
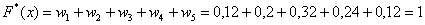
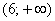
Накопленные относительные частоты удобно записывать в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева 1-е значение (красная стрелка), а каждое следующее получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения): 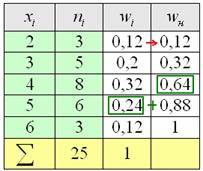
Вот, кстати, ещё один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
Саму функцию принято записывать в кусочном виде:
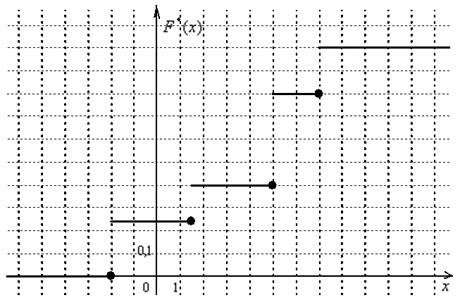
а её график представляет собой ступенчатую фигуру:
Эмпирическая функция распределения не убывает и принимает значения из промежутка 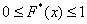
И сейчас мы автоматизируем процесс; видео, к сожалению, не вписалось по ширине, посему смотрим его на Ютубе:

Эмпирическая функция распределения 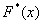
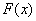
Миниатюрная задача для закрепления материала:
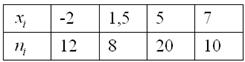
Дано статистическое распределение выборки
Составить эмпирическую функцию распределения, выполнить чертёж
Самостоятельно решить Пример 5 в Экселе, все числа и обозначения уже там.
Свериться с образцом можно ниже. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.
И я жду вас на третьем уроке, где речь пойдёт об интервальном вариационном ряде.
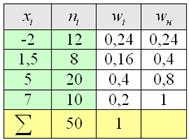
Пример 5. Решение: заполним расчётную таблицу:
Составим эмпирическую функцию распределения:
Выполним чертёж:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5