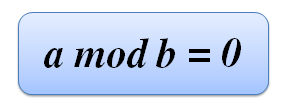Что такое див информатика
Что такое див информатика
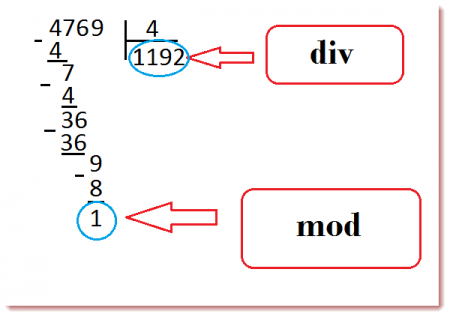
Оператор div и оператор mod
В этой статье речь пойдет о целочисленном делении и делении с остатком.
То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.
Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e
Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так
z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!
А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.
Например (40 / 6) с остатком = 4 с оператором mod будет такой
Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.
Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим
Что такое див информатика
В данной статье мы рассмотрим операторы mod и div, их применение при решении задач. Рассмотрим несколько примеров с решением, а также задачи для самостоятельного выполнения.
Успехов вам в программировании.
Переменная s будет равна 5.
Переменная s будет равна 2.
Использование mod при решении задач
Задача: определить, является ли число, введенное с клавиатуры, четным.
Чтобы ответить на этот вопрос нужно поделить число a с помощью mod на 2 (a mod 2) и сравнить это значение с нулем. Условие будет выглядеть так: a mod 2 = 0
Итак, чтобы узнать: делится ли число a на число b без остатка, нужно воспользоваться условием:
Задача: умножить последнюю цифру числа на 10 и результат вывести на экран.
Чтобы поместить последнюю цифру числа a в некоторую переменную необходимо поделить это число с помощью mod на 10. Получим: b:=a mod 10 — в переменной b окажется последняя цифра числа.
Если мы хотим отделить 2-е последние цифры числа, то должны делить с помощью mod на 100; если 3 — на 1000 и т.д.
Чтобы узнать, оканчивается ли число a на цифру b необходимо воспользоваться условием:
Задача: е с ли введенное с клавиатуры число оканчивается на 5 и делится на 7, то вывести «YES» иначе «NO»
С помощью рассмотренных условий и цикла со счетчиком можно решить следующую задачу:
посчитать количество чисел, которые кратны 9 и оканчиваются на 5 в диапазоне от 1 до 500
Использование оператора div при решении задач
Задача: дано трехзначное число. Выяснить, является ли оно палиндромом («перевертышем»), т.е. таким числом, десятичная запись которого читается одинаково слева направо и справа налево.
Отделить первую цифру числа можно, поделив его с помощью div на 100.
Отделить последнюю цифру можно, поделив его с помощью mod на 10. Вторая цифра нам не нужна для решения задачи, т.к. от нее не зависит, будет ли число палиндромом.
Задачи для самостоятельного выполнения:
Что такое див информатика
DIM X, L, M AS INTEGER
IF X MOD 2 = 0 THEN
if x mod 2 = 0 then
M := M + (x mod 10) div 2;
using namespace std;
Рассмотрим цикл, число шагов которого зависит от изменения переменной x:
while x > 0 do begin
Т. к. оператор div оставляет только целую часть от деления, то при делении на 10 это равносильно отсечению последней цифры.
Из приведенного цикла видно, что на каждом шаге от десятичной записи x отсекается последняя цифра до тех пор, пока все цифры не будут отсечены, то есть x не станет равно 0; поэтому цикл выполняется столько раз, сколько цифр в десятичной записи введенного числа, при этом число L столько же раз увеличивается на 1. Следовательно, конечное значение L совпадает с числом цифр в x. Для того, чтобы L стало L=3, x должно быть трёхзначным.
Теперь рассмотрим оператор изменения M:
if x mod 2 = 0 then
M:= M + (x mod 10) div 2;
Оператор mod оставляет только остаток от деления, при делении на 10 это последняя цифра x.
Условие x mod 2 = 0 означает следующее: чтобы M увеличилось, число x должно быть чётным.
Предположим, исходное x нечётное, тогда на первом шаге M = 0.
Если на втором шаге x также нечётное (вторая цифра исходного числа нечётная), то M = 0, причём каким бы ни было значение x на третьем шаге, мы не сможем получить M = 7, поскольку остаток от деления чётного числа на 10 не превосходит 8, а 8 / 2 = 4, следовательно, вторая цифра исходного x чётная.
Тогда первая цифра может принимать значения 2, 4, 6, 8, но мы ищем наибольшее x, поэтому сделаем первую цифру, равной 9, тогда наше предположение не удовлетворяет условию задачи, и последняя цифра исходного числа обязана быть чётной, т. е. исходное x чётно.
7 = 4 + 3, чему соответствуют цифры 8 и 6. Теперь, располагая цифры по убыванию, находим наибольшее возможное x: x = 986.
Mod и остаток — не одно и то же
Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!
Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.
Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.
В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»
Позовите ребят из секты «mod не остаток»! Это для вас.
Что такое mod?
Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.
Вот где мы попадаем в странную серую область.
Математика циферблата
Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.
Впрочем, не будем отклоняться от темы.
Остатки и математика циферблата
Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.
Рассмотрим такую задачу:
JavaScript с этим согласен:
Google согласен с первым утверждением, но не согласен со вторым:
Ruby согласен с Google:
Во имя Дейкстры, что здесь происходит?
Вращение часов назад
Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.
Но почему существует разница? Рассмотрим положительный делитель 19 mod 12 на часах:
Это известная вещь
Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать % операцией «остатка» (remainder), а не modulo:
Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.
Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:
Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.
А как на вашем языке?
Ну и что?
Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:
Система команд x86
Влияние команды на флаги и форматы команды:
Описание:
Команда DIV (Unsigned Divide) относится к группе команд целочисленной (или двоичной) арифметики (Binary Arithmetic Instructions) и производит целочисленное деление с остатком беззнаковых целочисленных операндов. Делимое, частное и остаток задаются неявно. Делимое является переменной в регистре (или регистровой паре) AX, DX:AX или EDX:EAX в зависимости от кода команды и атрибута размера операнда (что также определяет и разрядность делителя). Единственный явный операнд команды — операнд-источник (SRC), задающий делитель — может быть переменной в регистре или в памяти (r/m8, r/m16, r/m32). Целая часть частного помещается в регистр AL, AX или EAX в зависимости от заданного размера делителя (8, 16 или 32 бита). При этом остаток от целочисленного деления помещается в регистр AH, DX или EDX соответственно.
Действие команды DIV зависит от размера операнда-источника (SRC) следующим образом:
Размер
Делитель
Частное
Остаток
Делимое
Если частное, получаемое в результате деления, оказывается слишком велико, чтобы поместиться в целевом регистре-назначении (то есть имеет место переполнение), или если делитель равен нулю, то генерируется особая ситуация #DE.
Целочисленное частное округляется в сторону нуля. Абсолютная величина остатка всегда меньше, чем абсолютная величина делителя.
Команду DIV можно применять в вычислениях с числами в неупакованном двоично-десятичном формате (неупакованный BCD-формат). В этом случае необходимо использовать команду AAD непосредственно перед командой DIV, чтобы произвести так называемую ASCII-коррекцию перед делением и затем получить частное в таком же неупакованном BCD-формате, как и исходные операнды.
Дополнительной особенностью команды DIV является неопределенное значение большинства флагов в регистре EFLAGS в результате выполнения команды. То есть флаги не устанавливаются в соответствии с полученным частным или остатком.
Для деления целочисленных значений со знаком предназначены команды IDIV, FIDIV и FIDIVR.
Операция:
THEN #DE; (* Деление на нуль *)
IF (OperandSize = 8) (* Слово делим на байт *)
THEN #DE; (* Ошибка деления *)
IF (OperandSize = 16) (* Двойное слово делим на слово *)
THEN #DE; (* Ошибка деления *)
ELSE (* Учетверенное слово делим на двойное слово *)
IF ( temp > 0xFFFFFFFFh )
THEN #DE; (* Ошибка деления *)
EDX = EDX:EAX MOD SRC;
Особые ситуации защищенного режима:
#DE, если делимое равно нулю или частное слишком велико для размещения в регистре-назначении.
#GP(0), если при обращении к операнду в памяти в сегменте DS, ES, FS или GS используется нулевой селектор.
#GP(0), если любая часть операнда в памяти находится вне допустимого пространства эффективных адресов в сегменте CS, DS, ES, FS или GS.
#SS(0), если любая часть операнда в памяти находится вне допустимого пространства эффективных адресов в стековом сегменте SS.
Intel386 … :
#PF(Код ошибки) при страничной ошибке.
#UD при использовании префикса LOCK.
Intel486 … :
#AC(0) при невыровненной ссылке в память, если активирован контроль выравнивания (CR0.AM = 1, EFLAGS.AC = 1, CPL = 3).
Особые ситуации режима реальной адресации:
#DE, если делимое равно нулю или частное превышает разрядность регистра-назначения.
#GP, если любая часть операнда в памяти находится вне допустимого для реального режима пространства эффективных адресов в сегменте CS, DS, ES, FS или GS.
#SS, если любая часть операнда в памяти выходит за допустимую для реального режима верхнюю границу стекового сегмента SS.
Intel386 … :
#UD при использовании префикса LOCK.
Особые ситуации режима V86:
#DE, если делимое равно нулю или частное превышает разрядность регистра-назначения.
#GP(0), если любая часть операнда в памяти находится вне допустимого пространства эффективных адресов в сегменте CS, DS, ES, FS или GS.
#SS(0), если любая часть операнда в памяти находится вне допустимого пространства эффективных адресов в стековом сегменте SS.
Intel386 … :
#PF(Код ошибки) при страничной ошибке.
#UD при использовании префикса LOCK.
Intel486 … :
#AC(0) при невыровненной ссылке в память, если активирован контроль выравнивания (CR0.AM = 1, EFLAGS.AC = 1, CPL = 3).
Замечание:
Отдельные особенности существовали у процессоров 8086/8088 для генерации особой ситуации деления на нуль (#DE). В этих процессорах, в отличие от последующих моделей, точка возврата CS:IP, сохраняемая в стеке, не указывает на команду DIV, вызвавшую прерывание, — она указывает на следующую за ней команду.
К командам целочисленной арифметики относятся команды ADD, ADC, SUB, SBB, IMUL, MUL, IDIV, DIV, INC, DEC, NEG, CMP.
В свою очередь, сами названные команды целочисленной арифметики делятся на следующие подгруппы: