Что такое длина полуинтервала
Полуинтервал
Полуинтервал — множество точек прямой, заключённых между точками А и В, при этом одна из точек А или В не причисляются к полуинтервалу.
См. также
Полезное
Смотреть что такое «Полуинтервал» в других словарях:
полуинтервал — полуинтервал … Орфографический словарь-справочник
Полуинтервал — (математический) совокупность точек числовой оси, удовлетворяющих неравенствам а ≤ х … Большая советская энциклопедия
полуинтервал — множество точек х числовой оси, удовлетворяющих неравенствам а≤х … Энциклопедический словарь
ПОЛУИНТЕРВАЛ — множество точек х числовой оси, удовлетворяющих неравенствам а= Естествознание. Энциклопедический словарь
полуинтервал — полуинтерв ал, а … Русский орфографический словарь
полуинтервал — (2 м); мн. полуинтерва/лы, Р. полуинтерва/лов … Орфографический словарь русского языка
полуинтервал — полуинтерва/л, а … Слитно. Раздельно. Через дефис.
Суб — (лат. под) предлог, приставляемый к разным словам музыкальной терминологии. С. доминант четвертая ступень гаммы, последняя нота первого тетрахорда диатонической гаммы, Subsemitonium modi полуинтервал под тоникой, напр. si do, в котором si… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Таблица числовых промежутков: виды, обозначения, изображения
Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Каждый числовой промежуток характеризуется:
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x a включает в себя точки, которые расположены левее, а для x > a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.
Рассмотрим несколько примеров.
Для наглядного примера зададим числовой луч.
Рассмотрим рисунок, приведенный ниже.
Таблица числовых промежутков
Промежутки могут быть изображены в виде:
Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.
Числовые промежутки — виды, функции и примеры
Числовые промежутки представляют собой множества чисел на координатной прямой. Это ось, на которой расположены точки или переменные, имеющие определенные координаты. Для нее важно начало отсчета, выбранный единичный отрезок и направление, чтобы обозначать положительные и отрицательные значения.
Знакомство с координатами и числами происходит на уроках математики в 6 классе, но некоторые понятия вводятся уже с 1 класса. Понятия и обозначения используются на протяжении всего курса алгебры и геометрии. Знакомство с азами в средней школе позволит легко справляться со сложными задачами в будущем. Со временем проводятся вычисления со множествами чисел, это касается их пересечения и объединения.
Виды числовых промежутков
На координатной прямой можно выделить несколько видов промежутков. При этом они зависят от одной или двух переменных, расположенных на оси. Они служат границами. Сама прямая имеет координаты (-∞; +∞), то есть от минус бесконечности до плюс бесконечности.
Промежутки позволяют находить значения числовых выражений даже для учащихся младших классов. Выбирается место отсчета и единичный отрезок, что характеризует любую координатную прямую.
Чтобы выполнить простое арифметическое действие, нужно нарисовать нужное число отрезков. Чтобы сложить «2» и «3», достаточно отмерить сначала два, затем три выбранных единицы и сосчитать полученный результат. Так наглядно представляются простые математические операции для младших школьников.
На координатную прямую можно нанести известные значения и сравнить их, обращая внимание на положение. Так дети наглядно представляют, какое число меньше, а какое больше.
Открытый числовой луч
Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.
Точки расположены по одну сторону от определенной переменной, признанной началом координат.
Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:
Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».
Также можно охарактеризовать неравенством:
Знак зависит от расположения луча относительно А.
Замкнутый числовой луч
Замкнутый луч отличается от открытого тем, что к множеству относится А.
Также ему соответствует условие:
х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;
х ≥ А (значение больше или равно А) или [А; +∞).
При графическом изображении А в этом случае закрашивается, на рисунке она черная.
Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.
Числовой отрезок
Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.
При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.
Интервал
Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.
Обозначается, например, 5 Полуинтервал
Полуинтервал – интервал, при этом одна из точек, его ограничивающих, входит в него. То есть он закрыт с одной стороны. При этом неважно, какая из границ будет принадлежать интервалу, а какая нет.
Обозначаются с помощью двойных неравенств, при этом они называются нестрогими, так как используются знаки «больше или равно» или «меньше или равно». Одна из точек на графике не будет закрашена.
Все промежутки имеют обозначения и неравенства. Данные об этом собраны в таблице. Каждому виду соответствует графическое изображение.
Наглядное изображение поможет восприятию и закреплению материала.
Границы представлены а и b, они так и называются, граничными точками. При этом знаки ≥ и ≤ обозначаются квадратной скобкой. При графическом изображении такая граница закрашивается, это означает, что она входит в множество. Строгие неравенства соответствуют выколотым точкам на графиках.
Промежутки знакомят школьников с простыми неравенствами, строгими и нестрогими, которые необходимы для решения сложных математических задач.
Числовые отрезки, интервалы, полуинтервалы и лучи называют числовыми промежутками.
В) Числовая прямая
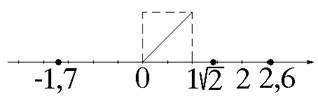
Рассмотрим числовую прямую (рис. 6):
Рассмотрим множество рациональных чисел
Каждое рациональное число изображается некоторой точкой на числовой оси. Так, на рисунке отмечены числа 
Докажем, что 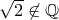
Доказательство. Пусть существует дробь 









Итак, не все точки числовой оси изображают рациональные числа. Те точки, которые не изображают рациональные числа, изображают числа, называемые иррациональными.
Любое число вида 


Числовые промежутки
Числовые отрезки, интервалы, полуинтервалы и лучи называют числовыми промежутками.


















 .
. .
. .
.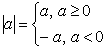


 . Это число принадлежит множеству х>1.
. Это число принадлежит множеству х>1.
 .
.
 называются коэффициентами квадратного уравнения.
называются коэффициентами квадратного уравнения.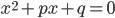 , первый коэффициент которого равен единице (
, первый коэффициент которого равен единице (  ).
).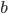 и
и  не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение
не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение 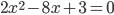 . Если один из коэффициентов
. Если один из коэффициентов  .Значение неизвестного
.Значение неизвестного  , при котором квадратное уравнение обращается в верное числовое равенство, называется корнем этого уравнения. Например, значение
, при котором квадратное уравнение обращается в верное числовое равенство, называется корнем этого уравнения. Например, значение 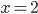 является корнем квадратного уравнения
является корнем квадратного уравнения  , потому что
, потому что 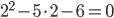 или
или  — это верное числовое равенство.Решить квадратное уравнение — это значит найти множество его корней.
— это верное числовое равенство.Решить квадратное уравнение — это значит найти множество его корней. [40]. При этом учитывается распределение вероятностей появления элементов в последовательности.
[40]. При этом учитывается распределение вероятностей появления элементов в последовательности.