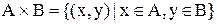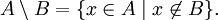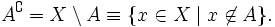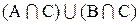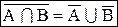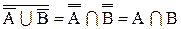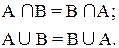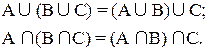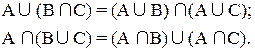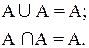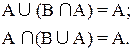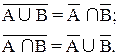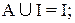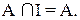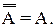Что такое дополнение множеств

Дополнение (математика)

Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.

Содержание

Разность множеств

Определение

Примеры

Свойства

Пусть A,B,C — произвольные множества. Тогда

Компьютерные реализации

Дополнение множества

Определение

Свойства

См. также

Полезное

Смотреть что такое «Дополнение (математика)» в других словарях:

Математика исламского средневековья — Данная статья часть обзора История математики. Арабский халифат (750 г.) Математика Востока, в отличие от древнегреческой математики, в … Википедия

Двойственность (математика) — Принцип, формулируемый в некоторых разделах математики и заключающийся в том, что каждому верному утверждению этого раздела отвечает двойственное утверждение, которое может быть получено из первого путём замены входящих в него понятий на другие,… … Википедия

Техническое образование (дополнение к статье) — В области высшего Т. образования в 1900 1907 гг. состоялись следующие важнейшие узаконения. 12 июня 1900 г. утверждено положение о Томском технологическом институте; помимо обычных отделений химического и механического в его составе открыты еще… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Ванновский (дополнение к статье) — (Петр Семенович) 1 января 1898 г. по болезни оставил пост военного министра и назначен членом государственного совета. В 1899 г. (20 февраля) В. было поручено всестороннее расследование причин беспорядков, происшедших в различных высших учебных… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Школы сельскохозяйственные (дополнение к статье) — 26 мая 1904 г. утверждено новое положение о сельскохозяйственном образовании, определяющее лишь общие основания для устройства с. х. учебных заведений, а министру земледелия и государственных имуществ предоставляющее издавать уставы, определяющие … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Область (математика) — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Путь (математика) — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия

Комплекс (математика) — У этого термина существуют и другие значения, см. Комплекс. Комплекс[1] (от лат. compléxus связь, сочетание) одно из основных понятий комбинаторной топологии. Комплексом называется частично упорядоченное правильным, рефлексивным… … Википедия

Пуанкаре, Анри — Анри Пуанкаре Henri Poincaré Дата рождения: 29 апреля 1854(1854 04 29) Место рождения: Нанси … Википедия

SAT — У этого термина существуют и другие значения, см. SAT (значения). SAT Reasoning Test (а также «Scholastic Aptitude Test» и «Scholastic Assessment Test», дословно «Школьный Оценочный Тест») стандартизованный тест для приема в высшие учебные… … Википедия

Источник

Дополнение (теория множеств)

Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.

Содержание

Разность множеств

Определение

Примеры

Свойства

Пусть A,B,C — произвольные множества. Тогда

Компьютерные реализации

Дополнение множества

Определение

Свойства

См. также

Полезное

Смотреть что такое «Дополнение (теория множеств)» в других словарях:

Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия

Наивная теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Содержание 1 Теория… … Википедия

Описательная теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Содержание 1 Теория… … Википедия

ДЕСКРИПТИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел теории множеств, изучающий внутреннее строение множеств в зависимости ют тех операций, при помощи к рых эти множества могут быть построены из множеств сравнительно простой природы (напр., замкнутых или открытых подмножеств данного… … Математическая энциклопедия

Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия

РЕКУРСИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел тео рии рекурсивных функций, в к ром рассматриваются и классифицируются подмножества натуральных чисел с алгоритмич. точки зрения, а также исследуются структуры, возникающие в результате такой классификации. Для каждого множества А, к рое… … Математическая энциклопедия

Принцип двойственности (теория множеств) — У этого термина существуют и другие значения, см. Принцип двойственности. Принцип двойственности в абстрактной теории множеств. Пусть дано множество М. Рассмотрим систему всех его подмножеств А, В, С и т. д. Справедливо следующее предложение:… … Википедия

Дополнение — В Викисловаре есть статья «дополнение» Дополнение может означать … Википедия

Теория моделей — Теория моделей раздел математической логики, который занимается изучением связи между формальными языками и их интерпретациями, или моделями. Название теория моделей было впервые предложено Тарским в 1954 году. Основное развитие теория … Википедия

МНОЖЕСТВ ТЕОРИЯ — Под множеством понимается совокупность каких либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов.… … Энциклопедия Кольера

Источник

Дополнение множества

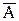
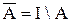
Множество , определяемое из соотношения

1.20

называют дополнением множества А (до универсального множества I)

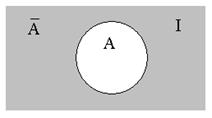
Графически дополнение множества А может быть представлено как показано на рис. 1.5.

Формальное определение дополнения множества А может быть записано как

1.21

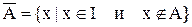
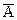
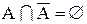
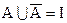
Из определения дополнения множества следует, что А и не имеют общих элементов, т.е.

1.22

Кроме того, 1.23

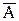
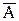
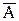
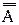
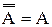
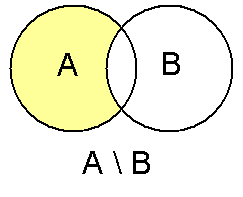
Из симметрии формул 1.22 и 1.23 следует, что не только является дополнением А, но и А является дополнением . Но дополнение есть . Таким образом 1.24

С помощью операции дополнения удобно представить разность множеств:

= , т.е 1.25

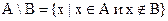
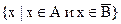
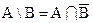
Принцип двойственности в алгебре множеств

В теории множеств и ее приложениях очень важную роль играет принцип двойственности, который основан на следующих двух соотношениях :

1. Дополнение объединений равно пересечению дополнений.

1.26

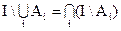
2. Дополнение пересечения равно объединению дополнений.

1.27

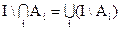
Принцип двойственности состоит в том, что из любого равенства, относящегося к системе подмножеств фиксированного множества I, совершенно автоматически может быть получено другое двойственное равенство путем замены всех рассматриваемых множеств их дополнениями, объединений множеств – пересечениями, а пересечений – объединениями.

Приведем доказательство соотношения 1.26.

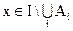
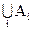
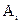
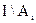
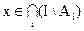
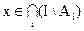
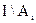
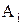
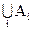
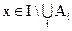
Пусть . Это означает, что х не входит в объединение , т.е. не входит ни в одно из множеств . Следовательно, х принадлежит каждому из дополнений и поэтому . Обратно: пусть , т.е. х входит в каждое . Тогда х не входит ни в одно из множеств , т.е. не принадлежит их объединению , но тогда . Равенство доказано. Аналогично доказывается равенство 1.27.

Тождества алгебры множеств

С помощью операций объединения, пересечения, дополнения из множеств можно составить различные алгебраические выражения. Обозначим через V(A,B,C) некоторое алгебраическое выражение, составленное из множеств А, В, С и представляющее собой некоторое множество.

Пусть W(A,B,C) – другое алгебраическое выражение, составленное из тех же множеств. Если оба алгебраических выражения представляют собой одно и тоже множество, то их можно приравнять друг к другу, получая алгебраическое тождество вида:

Такие тождества очень полезны при преобразовании алгебраических выражений над множествами.

1. Составим диаграммы Эйлера-Венна для выражений:

и

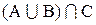
Из диаграмм видно, что оба выражения определяют одно и тоже множество, так что имеет место равенство1:

1.28

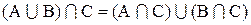
2. Составим диаграммы Эйлера-Венна для выражений

и .

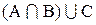
Из построенных диаграмм видно, что они отражают одно и тоже множество, следовательно, между выражениями можно поставить знак равенства:

= 1.29

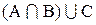
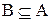
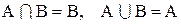
3. Легко убедиться, что если , то

. 1.30

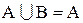
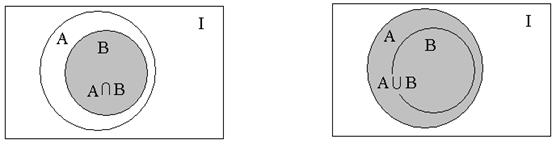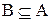
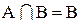
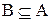
Действительно, все элементы множества В являются в то же время и элементами множества А (т.к. А включает В по определению). Следовательно, пересечение этих множеств, т.е. общая часть множеств А и В совпадает с В. В объединение множеств А и В множество В не внесет ни одного элемента, т.к. каждый элемент множества В является и элементом множества А (по определению), и следовательно . Соответствующие диаграммы Эйлера-Венна приведены на рис. 1.6.

; ;

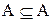
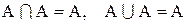
4. Полагая в 1.30 В = А и учитывая, что , получаем:

. 1.31

Установление тождеств алгебры множеств с помощью диаграмм Эйлера-Венна не всегда является удобным. Имеется более общий способ установления тождественности двух алгебраических выражений. Ранее было показано, что множество А равняется множеству В, если .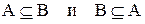

Пусть как и ранее через V(A,B,C) и W(A,B,C) обозначены два алгебраических выражения, получившихся путем применения операций объединения, пересечения и дополнения к множествам А, В, С. Тогда, чтобы доказать, что V=W достаточно показать и что . В свою очередь, чтобы показать, что , нужно убедиться, что из хÎV следует хÎW. Аналогично, чтобы показать, что , нужно убедиться, что из хÎW следует хÎV.

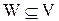
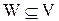
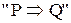
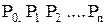
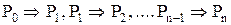
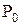
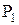
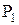
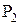
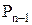
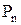
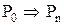
Следует заметить, что каждое из доказательств состоит из последовательности утверждений вида “если P, то Q” (если справедливо P, то справедливо и Q). Для удобства это утверждение записывается как и читается “из P следует Q”. Следовательно, если имеется последовательность такая, что (из следует , из следует , ….. следует ), то имеет место доказательство .

Воспользовавшись этим методом, докажем некоторые тождества.

1. Доказать, что .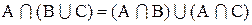

Доказательство:

(Скобки означают, что объединение следует вычислить перед пересечением) . Таким образом . (а)

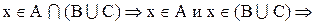
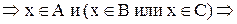
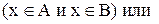
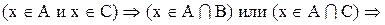
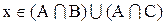
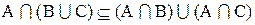
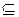
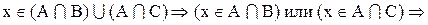
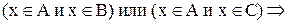
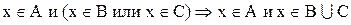
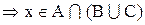
Теперь необходимо доказать включение в обратную сторону:

.

Следовательно, 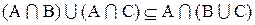. (б)

Тогда на основании полученных выражений (а) и (б) имеет место равенство:

.

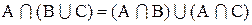
Аналогично доказывается и равенство .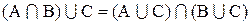

2. Доказать тождество:

. 1.32

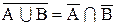
Доказательство:

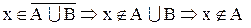
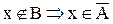
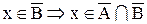
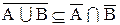
а. и и , т.е. ;

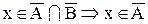
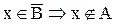
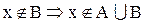
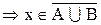
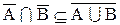
b. и и , т.е. ;

Следовательно, .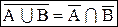

3. Доказать тождество:

. 1.33

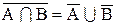
Доказательство:

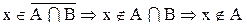
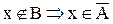
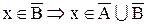
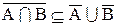
а. и и (или) , т.е. ;

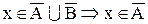
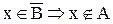
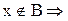
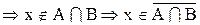
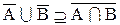
b. или и , т.е ;

Следовательно,

Тождества 1.32 и 1.33 играют важную роль в преобразовании алгебраических выражений алгебры множеств и особенно в математической логике. Их обычно называют тождествами де-Моргана или законами де-Моргана.

Конечно, для доказательств тождеств могут использоваться разные подходы. Докажем, например, тождество 1.33, основываясь на соотношении 1.32 и учитывая 1.24

Итак, необходимо доказать, что .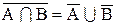

Приведем обе части равенства к одному виду. Выполняя операцию дополнения над обеими частями, получаем:

.

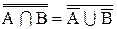
Но, учитывая соотношение 1.24 ( ), .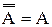

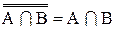
Для правой части на основании 1.32 имеем:

Итак, обе части приведены к одному виду, следовательно, тождество справедливо.

На основании вышеизложенных операций и определений приведем основные законы теории множеств :

1. Законы коммутативности (переместительный закон):

2. Законы ассоциативности (сочетательный закон):

3. Законы дистрибутивности (распределительный закон):

4. Законы идемпотетности:

5. Законы поглощения:

6. Законы де-Моргана:

7. Законы нуля и единицы:

Æ=A; Æ=Æ;

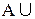
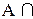
8. Закон двойного дополнения (отрицания):

Разбиение множества

Одной из наиболее часто встречающихся операций над множествами является операция разбиения множества на систему подмножеств.

Примеры:

1. Если N – множество натуральных чисел, а А и В – множества четных и нечетных чисел соответственно, то система будет разбиением множества N. Конечно, множество N можно разбить и на другие подмножества: множества чисел, делящихся на 2, на 3 и т.п.

2. Все множество студентов института можно разбить на отдельные подмножества, представляющие собой множества студентов группы (или факультета).

3. Продукция предприятия (а это есть множество) разбивается на продукцию первого сорта, второго сорта, исправимый брак, неисправимый брак, т.е. – на отдельные подмножества.

Рассмотрим некоторое множество А и систему множеств М = 1, X₂, X₃, …. X_n>.

Определение. Систему множеств М называют разбиением множества А, если удовлетворяются следующие условия:

1. Любое множество Х из М является подмножеством множества А:

.

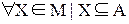
2. Любые два множества X_i и X_j из М являются непересекающимися:

Æ0.

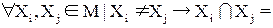
3. Объединение всех множеств, входящих в разбиение, дает множество А:

.

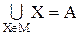
Упорядочение элементов и прямое произведение множеств

Упорядоченное множество

Наряду с понятием множества очень важным понятием является понятие упорядоченного множества или кортежа.

Кортежом называют последовательность элементов (совокупность элементов), в которой каждый элемент занимает определенное место. Сами элементы при этом называют компонентами кортежа (первая компонента, вторая компонента и т.д.).

Примерами кортежей могут быть: множество людей, стоящих в очереди; множество слов в фразе; числа, выражающие долготу и широту точки на местности; параметры, характеризующие состояние какого либо объекта, устройства и т.п.

Любая техническая система часто описывается множеством параметров, принимающих числовые значения. Т.е. система представляется некоторым набором параметров, характеризующих систему – множеством некоторых чисел. При этом устанавливают, какой параметр считать первым, какой вторым и т.д. Т.е. совокупность параметров представляется в виде упорядоченного множества – кортежа.

Число элементов кортежа называют его длиной. Для обозначения кортежа используют круглые скобки. Так, например, X = (x₁, x₂, …. х_n), или X = á x₁, x₂, …. х_n ñ – кортеж длины n c элементами x₁, x₂, …. x_n.

Кортежи длиной 2 называют парами, 3 – тройками, 4 – четверками, n –n-ками. Пустой кортеж обозначается ( ) или символом L. В отличии от обычного множества в кортеже могут быть и одинаковые элементы (два одинаковых слова в фразе, одинаковые числовые значения параметров системы и т.п.).

Упорядоченной парой называется двухэлементное множество, для которого указано, какой элемент является первым, какой – вторым и обозначается ( x₁, x₂)

Если рассматривать упорядоченные множества, элементами которых являются вещественные числа, то такие упорядоченные множества называют точками пространства или векторами. Так, кортеж х₁, х₂ –рассматривается как точка на плоскости или вектор.

х₂ х₁, х₂ Компоненты х₁, х₂ будут проекциями вектора на оси 1 и 2.

х₁ 1

Кортеж (х₁, х₂, х₃) рассматривается как точка в трехмерном пространстве, или как 3-х мерный вектор:

3

x₃ x₁, x₃

x₂, x₃ x₁, x₂, x₃ Если говорить о проекции кортежа сразу на оси, т.е. на координатную плоскость, то нетрудно увидеть, что

x₁ 1 Пр₁₂ (x₁, x₂, x₃) = x₁, x₂;

Обобщая эти понятия, видно, что упорядоченное n-элементное множество вещественных чисел (x₁, x₂, …. x_n) рассматривается как точка в n–мерном пространстве, называемом гиперпространством или n-мерным вектором. При этом, Пр_i (x₁, x₂, …. x_n)=x_i, i= 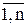1.

Два вектора равны, если они имеют одинаковую длину и их соответствующие компоненты равны, т.е. (a₁, a₂, …a_n) = (b₁, b₂, …b_n) Û «i a_i = b_i.

Прямое произведение множеств

Прямым произведением множеств А и В называют множество, обозначаемое 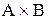и состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству А, а вторая – множеству В. Таким образом, элементами прямого произведения множеств являются двухэлементные кортежи вида (x,y).

Данное определение может быть записано в виде:

1.34

Источник