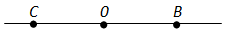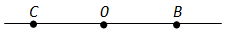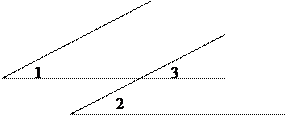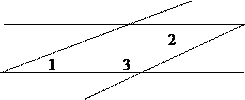Что такое дополнительные полупрямые
Что такое дополнительные полупрямые
Луч — это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой. Луч также называется полупрямой.
Любой луч имеет начало и направление. Начало луча, начальная точка или вершина луча — это точка, из которой исходит луч. Таким образом, у луча есть начало, но нет конца.
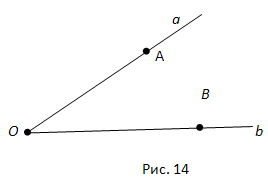
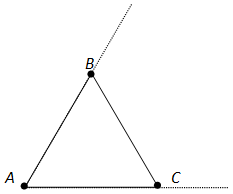
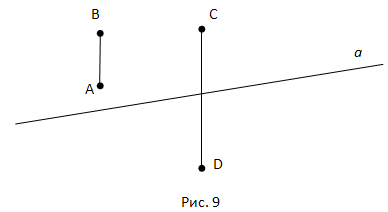
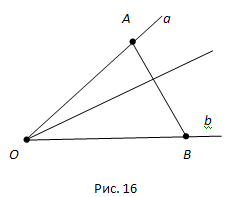
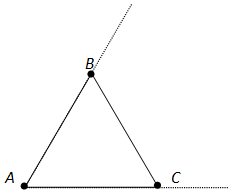
Рассмотрим три луча с общим началом:
Дополнительные лучи
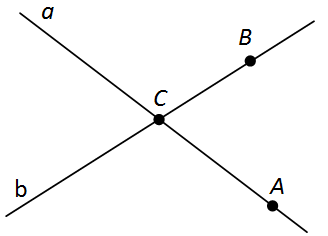
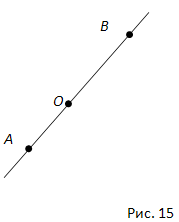
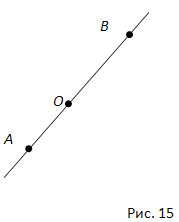
Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча:
Дополнительные лучи — это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой. Также можно сказать, что дополнительными называются лучи, дополняющие друг друга до прямой линии.
Обозначение лучей
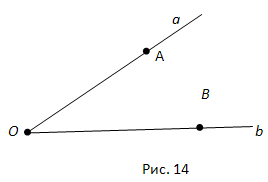
Луч обозначают одной строчной латинской буквой:
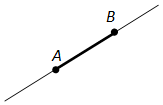
Также луч можно обозначить двумя точками, лежащими на нём:
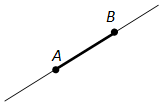
При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC.
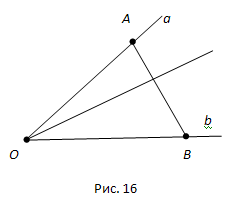
Посмотрим на следующий пример:
Луч с началом в точке A можно обозначить как AB или AC.
Что такое дополнительные полупрямые
§1. Контрольные вопросы
Вопрос 1. Приведите примеры геометрических фигур.
Ответ. Примеры геометрических фигур: треугольник, квадрат, окружность.
Вопрос 2. Назовите основные геометрические фигуры на плоскости.
Ответ. Основными геометрическими фигурами на плоскости являются точка и прямая.
Вопрос 4. Сформулируйте основные свойства принадлежности точек и прямых.
Ответ. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Вопрос 5. Объясните, что такое отрезок с концами в данных точках.
Ответ.Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок AB», то подразумевают отрезок с концами в точках A и B.
Вопрос 6. Сформулируйте основное свойство расположения точек на прямой.
Ответ. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Вопрос 7. Сформулируйте основные свойства измерения отрезков.
Ответ. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Вопрос 8. Что называется расстоянием между двумя данными точками?
Ответ. Длину отрезка AB называют расстоянием между точками A и B.
Вопрос 9. Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответ. Разбиение плоскости на две полуплоскости обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
Вопрос 10. Сформулируйте основное свойство расположения точек относительно прямой на плоскости.
Ответ. Прямая разбивает плоскость на две полуплоскости.
Вопрос 11. Что такое полупрямая или луч? Какие полупрямые называются дополнительными?
Ответ.Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой. Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называются дополнительными.
Вопрос 14. Как обозначается угол?
Ответ. Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трёх точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют знаком.
Вопрос 15. Какой угол называется развёрнутым?
Ответ. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развёрнутым.
Вопрос 16. Объясните, что означает выражение: «Полупрямая проходит между сторонами угла”.
Ответ.
Мы будем говорить, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.
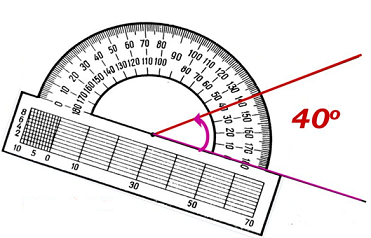
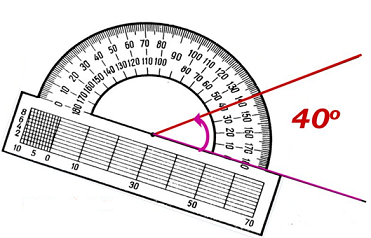
Вопрос 17. В каких единицах измеряются углы и с помощью какого инструмента? Объясните, как проводится измерение.
Ответ.Углы измеряются в градусах при помощи транспортира.
Вопрос 18. Сформулируйте основные свойства измерения углов.
Ответ. Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Вопрос 19. Сформулируйте основные свойства откладывания отрезков и углов.
Ответ. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
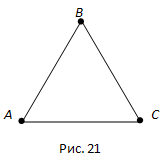
Вопрос 20. Что такое треугольник?
Ответ.
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — сторонами.
Вопрос 21. Что такое угол треугольника при данной вершине?
Ответ. Углом треугольника ABC при вершине A называется угол, образованный полупрямыми AB и AC. Так же определяются углы треугольника при вершинах B и C.
Вопрос 22. Какие отрезки называются равными?
Ответ. Отрезки называются равными, если их длины равны.
Вопрос 23. Какие углы называются равными?
Ответ. Углы называются равными, если их градусные меры равны.
Вопрос 24. Какие треугольники называются равными?
Ответ. Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
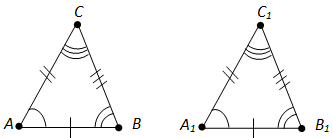
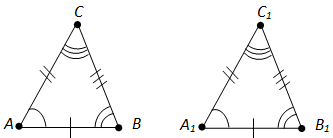
Вопрос 25. Как на рисунке отмечаются у равных треугольников соответствующие стороны и углы?
Ответ.На чертеже равные отрезки обычно отмечают одной, двумя или тремя чёрточками, а равные углы — одной, двумя или тремя дужками.
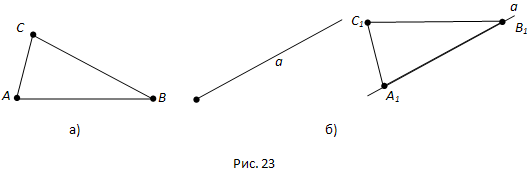
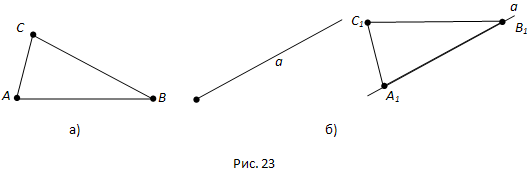
Вопрос 26. Объясните по рисунку 23 существование треугольника, равного данному.
Ответ.
Пусть мы имеем треугольник ABC и луч a (рис. 23, а). Переместим треугольник ABC так, чтобы его вершина A совместилась с началом луча a, вершина B попала на луч a, а вершина C оказалась в заданной полуплоскости относительно луча a и его продолжения. Вершины нашего треугольника в этом новом положении обозначим A1,B1,C1 (рис. 23, б).
Треугольник A1B1C1 равен треугольнику ABC.
Вопрос 27. Какие прямые называются параллельными? Какой знак используется для обозначения параллельности прямых?
Ответ.Две прямые называются параллельными, если они не пересекаются. Для обозначения параллельности прямых используется знак
Вопрос 28. Сформулируйте основное свойство параллельных прямых.
Ответ. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Вопрос 29. Приведите пример теоремы.
Ответ. Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.
Что такое дополнительные полупрямые
§1. Контрольные вопросы
Вопрос 1. Приведите примеры геометрических фигур.
Ответ. Примеры геометрических фигур: треугольник, квадрат, окружность.
Вопрос 2. Назовите основные геометрические фигуры на плоскости.
Ответ. Основными геометрическими фигурами на плоскости являются точка и прямая.
Вопрос 4. Сформулируйте основные свойства принадлежности точек и прямых.
Ответ. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Вопрос 5. Объясните, что такое отрезок с концами в данных точках.
Ответ.Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок AB», то подразумевают отрезок с концами в точках A и B.
Вопрос 6. Сформулируйте основное свойство расположения точек на прямой.
Ответ. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Вопрос 7. Сформулируйте основные свойства измерения отрезков.
Ответ. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Вопрос 8. Что называется расстоянием между двумя данными точками?
Ответ. Длину отрезка AB называют расстоянием между точками A и B.
Вопрос 9. Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответ. Разбиение плоскости на две полуплоскости обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
Вопрос 10. Сформулируйте основное свойство расположения точек относительно прямой на плоскости.
Ответ. Прямая разбивает плоскость на две полуплоскости.
Вопрос 11. Что такое полупрямая или луч? Какие полупрямые называются дополнительными?
Ответ.Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой. Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называются дополнительными.
Вопрос 14. Как обозначается угол?
Ответ. Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трёх точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют знаком.
Вопрос 15. Какой угол называется развёрнутым?
Ответ. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развёрнутым.
Вопрос 16. Объясните, что означает выражение: «Полупрямая проходит между сторонами угла”.
Ответ.
Мы будем говорить, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.
Вопрос 17. В каких единицах измеряются углы и с помощью какого инструмента? Объясните, как проводится измерение.
Ответ.Углы измеряются в градусах при помощи транспортира.
Вопрос 18. Сформулируйте основные свойства измерения углов.
Ответ. Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Вопрос 19. Сформулируйте основные свойства откладывания отрезков и углов.
Ответ. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
Вопрос 20. Что такое треугольник?
Ответ.
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — сторонами.
Вопрос 21. Что такое угол треугольника при данной вершине?
Ответ. Углом треугольника ABC при вершине A называется угол, образованный полупрямыми AB и AC. Так же определяются углы треугольника при вершинах B и C.
Вопрос 22. Какие отрезки называются равными?
Ответ. Отрезки называются равными, если их длины равны.
Вопрос 23. Какие углы называются равными?
Ответ. Углы называются равными, если их градусные меры равны.
Вопрос 24. Какие треугольники называются равными?
Ответ. Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
Вопрос 25. Как на рисунке отмечаются у равных треугольников соответствующие стороны и углы?
Ответ.На чертеже равные отрезки обычно отмечают одной, двумя или тремя чёрточками, а равные углы — одной, двумя или тремя дужками.
Вопрос 26. Объясните по рисунку 23 существование треугольника, равного данному.
Ответ.
Пусть мы имеем треугольник ABC и луч a (рис. 23, а). Переместим треугольник ABC так, чтобы его вершина A совместилась с началом луча a, вершина B попала на луч a, а вершина C оказалась в заданной полуплоскости относительно луча a и его продолжения. Вершины нашего треугольника в этом новом положении обозначим A1,B1,C1 (рис. 23, б).
Треугольник A1B1C1 равен треугольнику ABC.
Вопрос 27. Какие прямые называются параллельными? Какой знак используется для обозначения параллельности прямых?
Ответ.Две прямые называются параллельными, если они не пересекаются. Для обозначения параллельности прямых используется знак
Вопрос 28. Сформулируйте основное свойство параллельных прямых.
Ответ. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Вопрос 29. Приведите пример теоремы.
Ответ. Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.
Перпендикулярные прямые



Лекция №1
Элементарная геометрия
Построение курса геометрии. Основные понятия геометрии.
Геометрия – математическая дисциплина, рассматривающая и изучающая свойства различных объектов, расположенных определенным образом в пространстве.
Как и в любой математической дисциплине, определить все понятия, встречающиеся в геометрии, невозможно. Поэтому при любом построении курса элементарной геометрии приходится выделять несколько геометрических понятий, которые берутся за основные, первичные, или неопределяемые. Считается, что эти понятия обладают известными свойствами и зависимостями, которые принимаются без доказательства и называются аксиомами.
К таким неопределяемым понятиям в элементарной геометрии относятся:
· отношение принадлежности для точек, прямых и плоскостей, выражаемое словом «принадлежать»
· отношение порядка для точек на прямой, выражаемой словом «лежать между»
· длина для отрезков и
· градусная мера для углов
Все что предполагается известным об этих понятиях выражается аксиомами. впервые систему аксиом мы встречаем в «Началах» Евклида, однако его система аксиом была неполной.
Современная система аксиом состоит из пяти групп. Например:
· Через любые две точки можно провести прямую и притом только одну
· Через любые три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну
· Если точка В лежит между точками А и С, то все три точки принадлежат одной прямой
· Из трех точек прямой только одна лежит между двумя другими
· Через данную точку вне данной прямой можно провести на плоскости не более одной прямой, не пересекающей данную
С помощью основных понятий определяются все остальные понятия. Все предложения о свойствах геометрических фигур, не содержащиеся в аксиомах, должны быть доказаны чисто логическим выводом из этих аксиом. Такие предложения называются теоремами.
Предложением, обратным данному, называется другое предложение, в котором заключение полностью или частично совпадает с условием первого предложения и обратно.
Следствием называется предложение, непосредственно вытекающее из теоремы.
Леммой называется подготовительное предложение, вводимое для того, чтобы облегчить доказательство последующего предложения.
Строение курса геометрии можно охарактеризовать так:
1. Перечисляются основные неопределяемые понятия геометрии
2. Формулируются аксиомы
3. На основе введенных понятий даются определения всем остальным геометрическим понятиям
4. На основе аксиом и определений доказываются аксиомы, которые в свою очередь используются для доказательства других теорем в курсе геометрии.
Простейшие геометрические фигуры и их свойства
Отрезок
Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками. Эти точки называются концами отрезка.
Свойства отрезка описываются в следующих двух аксиомах:
· Из трех точек на прямой одна и только одна лежит между двумя другими
· Каждый отрезок имеет длину большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Длину отрезка также называют расстоянием между концами этого отрезка
Полупрямая (луч)
Полупрямой называется часть прямой, которая состоит из всех точек прямой, лежащих по одну сторону от данной ее точки. Эту точку называют начальной точкой полупрямой.
Две полупрямые одной прямой с общей начальной точкой называются дополнительными.
Следующая аксиома связывает отрезки и полупрямые:
· На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и только один
Полуплоскость
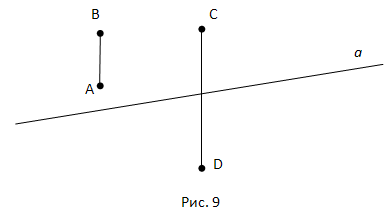
· Прямая разбивает плоскость на две полуплоскости. Это разбиение обладает следующим свойством: если концы какого-либо отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямой; если концы отрезка лежат в разных полуплоскостях, то отрезок пересекается с прямой.
Угол
Углом называется фигура, которая состоит из точки (вершины угла) и двух различных полупрямых, исходящих из этой точки (сторон угла)
основное свойство измерения углов описывается следующей аксиомой:
· Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°.
Развернутый угол – угол образованный двумя дополнительными полупрямыми.
· Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Говорят, что луч лежит между сторонами угла, если он пересекает любой отрезок с концами на сторонах угла.
· От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой и притом только один
Биссектрисой угла называется луч, который исходит из его вершины, проходит между его сторонами и делит угол пополам.
Два угла называются смежными, если у них одна сторона общая, а две другие – дополнительные полупрямые.
Теорема: Сумма смежных углов равна 180°.
Следствие1: Если два угла равны, то смежные с ними углы равны
Следствие2: Если угол неразвернутый, то его градусная мера меньше 180°.
Угол, градусная мера которого равна 90°, называется прямым.
Следствие3: угол, смежный с прямым – прямой.
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми для сторон другого угла.
Теорема: Вертикальные углы равны
Параллельные прямые
Две прямые на плоскости называются параллельными, если они не пересекаются.
Ранее указанная аксиома параллельности прямых выражает основное свойство параллельных прямых.
Теорема: Две прямые, параллельные третьей, параллельны между собой
При пересечении двух прямых секущей образуются следующие пары углов:

Внутренние накрестлежащие – 2 пары
Внутренние односторонние – 2 пары
Соответственные – 4 пары
Признаки параллельности прямых:
1. Если внутренние накрестлежащие углы равны, то прямые параллельны
2. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны
3. Если соответственные углы равны, то прямые параллельны.
Следствие: Две прямые, перпендикулярные к одной и той же прямой, параллельны между собой.
Для признаков параллельности прямых справедливы и обратные теоремы, которые являются свойствами параллельных прямых. Сформулируйте их
Теорема Фалеса: Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

следовательно, В1В2=В2В3.
Теорема: Два угла, стороны которых соответственно параллельны, равны, или их сумма равна 180°, смотря по тому, имеют ли оба угла одинаковое или различные направления.
Доказательство: Рассмотрим все возможные случаи расположения таких углов:
1) 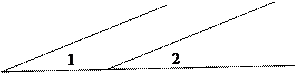
2) 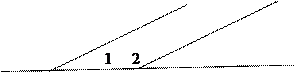
3) Ð1=Ð3 как соответственные углы при параллельных прямых.
Ð2=Ð3 как соответственные углы при параллельных прямых.
4) Ð2=Ð3 как соответственные углы при параллельных прямых
Ð1+Ð3=180° как односторонние углы при параллельных прямых
5) Ð1+Ð3=180° как односторонние углы при параллельных прямых
Отсюда получаем что Ð1=Ð2.
Теорема: Два угла, стороны которых соответственно перпендикулярны друг другу, равны, или их сумма равна 180°, в зависимости от того, имеют ли оба угла одинаковое направление или различные.
Перпендикулярные прямые
Две прямые называются перпендикулярными, если они пересекаются пол прямым углом.
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, имеющий концом их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Теорема: Через каждую точку прямой можно провести перпендикулярную ей прямую и притом только одну.
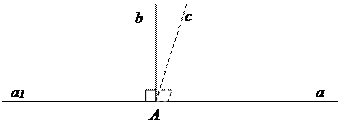
Пусть АÎа. Докажем, что через точку А можно провести b^a. Обозначим через а1 одну из полупрямых прямой а с началом в точке А. Отложим от полупрямой а1 угол Ð(а1b)=90°. Тогда прямая содержащая полупрямую b будет перпендикулярна прямой а.
Докажем единственность. Допустим, что существует другая прямая, также проходящая через точку А перпендикулярно прямой а. Обозначим через с полупрямую этой прямой, лежащую в одной полуплоскости с лучом b. Получим противоречие аксиоме, что в данную полуплоскость от данной полупрямой можно отложить только один угол с заданной градусной мерой. Таким образом, перпендикуляр единственен.
Теорема: Через точку, не лежащую на прямой, можно провести перпендикуляр к этой прямой и только один.

Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.
Расстоянием между параллельными прямыми называется расстояние от какой-либо точки взятой на на одной из параллельных прямых, до другой прямой.
Наклонной к данной прямой называется отрезок, имеющий концами точки пересечения этой прямой с данной и перпендикуляром к данной прямой.
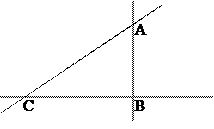
С – основание наклонной
Если к прямой из одной точки проведены наклонная и перпендикуляр, то
1) Любая наклонная больше перпендикуляра
2) Равные наклонные имеют равные проекции
3) Из двух наклонных больше та, у которой проекция больше.
(следует из теоремы Пифагора – доказать самостоятельно)
Прямую, проходящую через середину отрезка перпендикулярно к нему называют серединным перпендикуляром.
Теорема: Любая точка, лежащая на серединном перпендикуляре к отрезку одинаково удалена от концов этого отрезка.