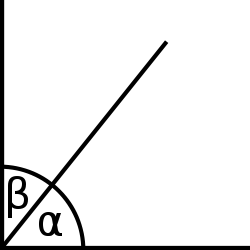
Что такое дополнительные углы

Дополнительные углы: какие и как рассчитываются, примеры, упражнения

Содержание:

Например, два угла, примыкающие к гипотенузе прямоугольного треугольника, дополняют друг друга, поскольку сумма их мер равна 90º. В этом отношении очень показателен следующий рисунок:

Всего на рисунке 1 показано четыре угла. α и β дополняют друг друга, так как они смежный и их сумма составляет прямой угол. Аналогично β дополняет γ, из чего следует, что γ и α имеют одинаковую меру.

Теперь, поскольку сумма α и δ равна 90 градусам, можно сказать, что α и δ дополняют друг друга. Более того, поскольку β и δ имеют одно и то же дополнительное α, можно сказать, что β и δ имеют одинаковую меру.

Примеры дополнительных углов

В следующих примерах предлагается найти неизвестные углы, отмеченные вопросительными знаками на рисунке 2.

— Примеры A, B и C

Следующие ниже примеры приведены в порядке сложности.

Пример А

На рисунке выше мы видим, что смежные углы α и 40º в сумме составляют прямой угол. То есть α + 40º = 90º, следовательно, α = 90º- 40º = 50º.

Пример Б

Пример C

Из рисунка 2C видно, что сумма γ + 15º + 15º = 90º. Другими словами, γ является дополнительным к углу 30º = 15º + 15º. Так что:

— Примеры D, E и F

В этих примерах задействовано больше углов. Чтобы найти неизвестные, читатель должен применять понятие дополнительного угла столько раз, сколько необходимо.

Пример D

Наконец, Z является дополнительным к Y. Из всего вышесказанного следует, что:

Пример E

Углы δ и 2δ дополняют друг друга, поэтому δ + 2δ = 90º.

То есть 3δ = 90º, что означает, что δ = 90º / 3 = 30º.

Пример F

Если мы назовем угол между que и 10º U, то U будет дополнительным к ним обоим, потому что наблюдается, что их сумма составляет прямой угол. Из чего следует, что U = 80º. Поскольку U является дополнительным к ω, то ω = 10º.

Упражнения

Ниже предлагаются три упражнения. Во всех из них необходимо найти значение углов A и B в градусах, чтобы выполнялись соотношения, показанные на рисунке 3.

— Упражнение 1

Определите значения углов A и B из части I) рисунка 3.

Решение

Из показанного рисунка видно, что A и B дополняют друг друга, поэтому A + B = 90º. Подставим выражение для A и B как функцию от x, приведенное в части I):

(x / 2 + 7) + (2x + 15) = 90

Затем члены группируются соответствующим образом, и получается простое линейное уравнение:

Вычитая 22 в обоих членах, получаем:

И, наконец, значение x очищается:

Теперь угол A находится путем подстановки значения X:

A = (136/5) / 2 +7 = 103/5 = 20,6 º.

B = 2 * 136/5 + 15 = 347/5-я = 69,4º.

— Упражнение 2.

Найдите значения углов A и B изображения II, рисунок 3.

Решение

Подобные термины сгруппированы вместе, чтобы получить уравнение:

Разделив обоих членов на 6, вы получите:

Отсюда следует, что x = 10º.

— Упражнение 3.

Определите значения углов A и B из части III) рисунка 3.

Решение

Снова фигура тщательно анализируется, чтобы найти дополнительные углы. В этом случае мы имеем A + B = 90 градусов. Подставляя выражения для A и B как функцию от x, приведенного на рисунке, мы имеем:

Разделив оба члена на 3, получим следующее:

Отсюда следует, что x = 20º.

Перпендикулярные боковые углы

Говорят, что два угла перпендикулярные стороны если у каждой стороны есть соответствующий перпендикуляр на другой. Следующий рисунок поясняет концепцию:

На рисунке 4, например, наблюдаются углы α и θ. Теперь обратите внимание, что каждому углу соответствует перпендикуляр под другим углом.

Также видно, что α и θ имеют одинаковый дополнительный угол z, поэтому наблюдатель немедленно заключает, что α и θ имеют одинаковую меру. Тогда кажется, что если два угла имеют стороны, перпендикулярные друг другу, они равны, но давайте рассмотрим другой случай.

Теперь рассмотрим углы α и ω. Эти два угла также имеют соответствующие перпендикулярные стороны, однако нельзя сказать, что они имеют одинаковую величину, поскольку один острый, а другой тупой.

Обратите внимание, что ω + θ = 180º. Кроме того, θ = α. Если вы замените это выражение на z в первом уравнении, вы получите:

Общее правило для углов перпендикулярных сторон

Из вышеизложенного можно установить правило, которое выполняется до тех пор, пока углы имеют перпендикулярные стороны:

Если два угла имеют взаимно перпендикулярные стороны, то они равны, если они оба острые или оба тупые. В противном случае, если один острый, а другой тупой, то они являются дополнительными, то есть складываются в 180º.

Применяя это правило и обращаясь к углам на рисунке 4, мы можем утверждать следующее:

С углом ω, дополнительным к α, β, θ и φ.

Ссылки

Какой была повседневная жизнь ольмеков?

От застенчивости до социофобии: что это такое и как к ним относятся

Источник

Дополнительные углы

Дополнительные углы́ — это пара углов, которые дополняют друг друга до 90 градусов.

Если два дополнительных угла являются соседними (т.е. имеют общую вершину и разделяются только одной стороной), их не общие стороны образуют прямой угол.

В евклидовой геометрии два острых угла прямоугольного треугольника являются дополнительными, потому что сумма внутренних углов треугольника составляет 180 градусов, а прямой угол равен 90 градусам.

Тригонометрические соотношения

Синус одного из углов равен косинусу его дополнительного угла. Если углы A и B являются дополнительными, то верны равенства: и .

Тангенс одного из углов равен котангенсу его дополнительного угла. Тангенсы дополнительных углов обратны друг другу.

Секанс одного из углов равен косекансу его дополнительного угла.

Префикс «ко-» в названиях некоторых тригонометрических функций происходит лат. complementum — дополнение.

См. также

Ссылки

Полезное

Смотреть что такое «Дополнительные углы» в других словарях:

ДОПОЛНИТЕЛЬНЫЕ УГЛЫ — ДОПОЛНИТЕЛЬНЫЕ УГЛЫ, два угла, сумма которых равна прямому углу (90°). Углы, сумма которых равна 180°, называются дополнительными … Научно-технический энциклопедический словарь

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

Хетцер — Jagdpanzer 38 Классификация истребитель тан … Википедия

Требования — 5.2 Требования к вертикальной разметке 5.2.1 На поверхность столбиков, обращенную в сторону приближающихся транспортных средств, наносят вертикальную разметку по ГОСТ Р 51256 в виде полосы черного цвета (рисунки 9 и 10) и крепят световозвращатели … Словарь-справочник терминов нормативно-технической документации

Прист (САУ) — У этого термина существуют и другие значения, см. Прист … Википедия

ГОСТ 24867-81: Руководство по летной эксплуатации самолетов гражданской авиации. Общие требования к содержанию, построению, изложению и оформлению — Терминология ГОСТ 24867 81: Руководство по летной эксплуатации самолетов гражданской авиации. Общие требования к содержанию, построению, изложению и оформлению оригинал документа: 4.4. Брошюровка, переплет 4.4.1. В зависимости от общего объема… … Словарь-справочник терминов нормативно-технической документации

Автомобильная светотехника — Автомобильная светотехника комплекс световой техники, использующийся для сигнализации и освещения. Автомобильное освещение монтируется в передней, в задней, а также в боковых частях транспортного средства в виде фар или фонарей. Установка… … Википедия

Требования к содержанию раздела — 2.8. Требования к содержанию раздела 06. «Действия в аварийных ситуациях» 06.1. Аварийные контрольные карты. 06.1.1. Сводка Аварийных контрольных карт. 06.1.2. Правила пользования Аварийными контрольными картами. 06.2. Пожар двигателя. 06.2.1.… … Словарь-справочник терминов нормативно-технической документации

Танк Т-34 — Рождение тридцатьчетверки Массовые танки Красной Армии Т 26 и БТ по своим тактико техническим данным были вполне на уровне требований середины 30 х годов и вполне удовлетворяли наших танкистов. Их производство развернулось в 1934 36 гг,… … Энциклопедия техники

Малые противолодочные корабли проекта 1124 — У этого термина существуют и другие значения, см. Проект 1124. Малые противолодочные корабли проекта 1124 … Википедия

Источник

Что такое дополнительные углы

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОСТРОГО УГЛА.

§ 97. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ДОПОЛНИТЕЛЬНЫХ УГЛОВ.

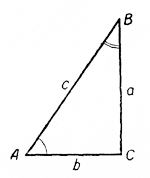
Дополнительными углами называются два угла, которые в сумме составляют 90°. Такими углами, в частности, являются острые углы прямоугольного треугольника.

Углы А и В в прямоугольном треугольнике АСВ (черт. 397) являются дополнительными углами, так как

Рассмотрим соотношения между тригонометрическими функциями дополнительных углов.

1) ; , т. e. cинус данного угла равен косинусу дополнительного угла.

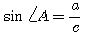
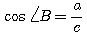
2) ; , т.е. косинус данного угла равен синусу дополнительного угла.

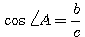
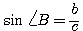
3) ; ,т.е. тангенс данного угла равен котангенсу дополнительного угла.

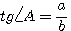
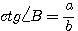
4) ; ,т.e. котангенс данного угла равен тангенсу дополнительного угла.

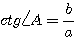
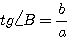
Знание соотношений между тригонометрическими функциями дополнительных углов важно для понимания устройства тригонометрических таблиц.

Источник

ДОПОЛНИТЕЛЬНЫЕ УГЛЫ

Смотреть что такое «ДОПОЛНИТЕЛЬНЫЕ УГЛЫ» в других словарях:

Дополнительные углы — Пара дополнительных углов, дополняющих друг друга до 90 градусов Дополнительные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два дополнительных угла являются с … Википедия

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

Хетцер — Jagdpanzer 38 Классификация истребитель тан … Википедия

Требования — 5.2 Требования к вертикальной разметке 5.2.1 На поверхность столбиков, обращенную в сторону приближающихся транспортных средств, наносят вертикальную разметку по ГОСТ Р 51256 в виде полосы черного цвета (рисунки 9 и 10) и крепят световозвращатели … Словарь-справочник терминов нормативно-технической документации

Прист (САУ) — У этого термина существуют и другие значения, см. Прист … Википедия

ГОСТ 24867-81: Руководство по летной эксплуатации самолетов гражданской авиации. Общие требования к содержанию, построению, изложению и оформлению — Терминология ГОСТ 24867 81: Руководство по летной эксплуатации самолетов гражданской авиации. Общие требования к содержанию, построению, изложению и оформлению оригинал документа: 4.4. Брошюровка, переплет 4.4.1. В зависимости от общего объема… … Словарь-справочник терминов нормативно-технической документации

Автомобильная светотехника — Автомобильная светотехника комплекс световой техники, использующийся для сигнализации и освещения. Автомобильное освещение монтируется в передней, в задней, а также в боковых частях транспортного средства в виде фар или фонарей. Установка… … Википедия

Требования к содержанию раздела — 2.8. Требования к содержанию раздела 06. «Действия в аварийных ситуациях» 06.1. Аварийные контрольные карты. 06.1.1. Сводка Аварийных контрольных карт. 06.1.2. Правила пользования Аварийными контрольными картами. 06.2. Пожар двигателя. 06.2.1.… … Словарь-справочник терминов нормативно-технической документации

Танк Т-34 — Рождение тридцатьчетверки Массовые танки Красной Армии Т 26 и БТ по своим тактико техническим данным были вполне на уровне требований середины 30 х годов и вполне удовлетворяли наших танкистов. Их производство развернулось в 1934 36 гг,… … Энциклопедия техники

Малые противолодочные корабли проекта 1124 — У этого термина существуют и другие значения, см. Проект 1124. Малые противолодочные корабли проекта 1124 … Википедия

Источник

Метод вспомогательного угла в тригонометрических уравнениях

На уроках алгебры учителя рассказывают, что существует небольшой (на самом деле — очень даже большой) класс тригонометрических уравнений, которые не решаются стандартными способами — ни через разложение на множители, ни через замену переменной, ни даже через однородные слагаемые. В этом случае в дело вступает принципиально другой подход — метод вспомогательного угла.

Что это за метод и как его применять? Для начала вспомним формулы синуса суммы/разности и косинуса суммы/разности:

\[\begin& \sin \left( \alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\& \cos \left( \alpha \pm \beta \right)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\\end\]

Думаю, эти формулы хорошо знакомы вам — из них выводятся формулы двойного аргумента, без которых в тригонометрии вообще никуда. Но давайте теперь рассмотрим простое уравнение:

Разделим обе части на 5:

\[\begin& \cos \alpha \sin x+\sin \alpha \cos x=1 \\& \sin \left( \alpha +x \right)=1 \\\end\]

Сегодня мы будем разбирать решение тригонометрических уравнений, а, точнее, один-единственный прием, который называется «метод вспомогательного угла». Почему именно этот метод? Просто потому, что за последние два-три дня, когда я занимался с учениками, которым рассказывал о решении тригонометрических уравнений, и мы разбирали, в том числе, метод вспомогательного угла, и все ученики как один допускают одну и ту же ошибку. А ведь метод вообщем-то несложный и, более того, это один из основных приемов в тригонометрии. Поэтому многие тригонометрические задачи иначе как методом вспомогательного угла вообще не решаются.

Поэтому сейчас для начала мы рассмотрим пару простеньких задач, а потом перейдем к задачам посерьезней. Однако все эти они так или иначе потребуют от нас применение метода вспомогательного угла, суть которого я расскажу уже в первой конструкции.

Решение простых тригонометрических задач

Пример № 1

Немного преобразуем наше выражение:

\[\sqrt<3>\cdot \sin 2x-\cos 2x=1\]

\[\sin \left( \alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \]

Вернемся к нашему примеру. Все сведем к синусу разности. Но для начала уравнение необходимо немного преобразовать. Найдем коэффициент:

$\sqrt$ — это тот самый коэффициент, на который необходимо разделить обе части уравнения, чтобы перед синусом и косинусом появились числа, которые сами по себе являются синусами и косинусами. Давайте разделим:

Теперь перед нами формула синуса разности. Мы можем написать так:

Перед нами простейшая классическая тригонометрическая конструкция. Напомню:

Это и запишем для нашего конкретного выражения:

Нюансы решения

Итак, что нужно делать, если вам попалось подобный пример:

В связи с этим у внимательных учеников наверняка возникнет два вопроса.

Метод вспомогательного угла — это инструмент, который помогает свести «некрасивое» уравнение к вполне адекватному и «красивому».

Пример № 2

Нам потребуется только первые выкладки. Давайте приступим к работе над задачей:

\[\sqrt<3>\cdot \sin 2x+2\cdot \frac<1-\cos 2x><2>-1=2\cos x\]

\[\sqrt<3>\cdot \sin 2x+1-\cos 2x-1=2\cos x\]

\[\sqrt<3>\cdot \sin 2x-\cos 2x=2\cos x\]

Перепишем с учетом этого факта:

\[\frac<\sqrt<3>><2>\cdot \sin 2x-\frac<1><2>\cdot \cos 2x=\cos x\]

Внесем «минус» в скобку хитрым способом. Для этого заметим следующее:

Чтобы решить подобною задачу, нужно вспомнить такое:

\[\cos \alpha =\cos \beta \]

\[\left[ \begin& \alpha =\beta +2\text< >\!\!\pi\!\!\text< >n \\& \alpha =-\beta +2\text< >\!\!\pi\!\!\text< >n \\\end \right.\]

Разберемся с нашим примером:

Давайте посчитаем каждое из этих уравнений:

Запишем окончательный ответ:

Нюансы решения

На самом деле, это выражение решается множеством различных способов, однако именно метод вспомогательного угла является в данном случае оптимальным. Кроме того, на примере данной конструкции хотелось бы обратить ваше внимание еще на несколько интересных приемов и фактов:

Разбор более сложных задач

Пример № 1

Преобразуем первое слагаемое:

\[\sin 3x=\sin \left( 2x+x \right)=\sin 2x\cdot \cos x+\cos 2x\cdot \sin x\]

\[=2\left( 1-\cos 2x \right)\cdot \sin x\]

А теперь подставим все это в нашу исходную конструкцию:

\[\sin 2x\cos x+\cos 2x\sin x+2\sin x-2\cos x\sin x+4\cos x=5\]

\[\sin 2x\cos x-\operatorname-cos2\sin x+2\sin x+4\cos x=5\]

\[\sin \left( 2x-x \right)+2\sin x+4\cos x=5\]

Давайте введем нашу поправку:

\[\sin x\cdot \cos \varphi +\cos x\cdot \sin \varphi =1\]

\[\sin \left( x+\varphi \right)=1\]

Это частный случай, простейшая тригонометрическая конструкция:

Начертим радар и посмотрим, где такие значения встречаются:

Возвращаясь к нашему выражению, мы напишем следующее:

Но и эту запись можно немного оптимизировать. Поскольку мы знаем следующее:

то в нашем случае можно записать так:

Пример № 2

Здесь потребуется еще более глубокое понимание методик решения стандартных задач без тригонометрии. Но для решения этого примера мы также используем метод вспомогательного угла.\[\]

\[5+2\sin 2x-5\cos x=5\sin x\]

Первое, что бросается в глаза — здесь нет степеней выше первой и поэтому ничего нельзя разложить по формулам разложения степеней. Воспользуется обратными выкладками:

\[5+4\sin x\cos x-5\cos x-5\sin x=0\]

\[3+2+4\sin x\cos x-5\left( \sin x+\cos x \right)=0\]

\[3+2\left( 1+2\sin x\cos x \right)-5\left( \sin x\cos x \right)=0\]

\[3+2\left( <<\sin >^<2>>x+2\sin x\cos x+co<^<2>>x \right)-5\left( \sin x+\cos x \right)=0\]

Что дает нам такая запись? Дело в том, что в первой скобке стоит точный квадрат. Свернем его и получим:

Предлагаю ввести новую переменную:

В этом случае мы получим выражение:

\[\left[ \begin& \sin x+\cos x=\frac<3> <2>\\& \sin x+\cos x=1 \\\end \right.\]

Разбираемся с каждым из этих выражений.

Первое уравнение корней не имеет, и для доказательства этого факта нам поможет иррациональность в знаменателе. Заметим следующее:

Разбираемся со вторым:

Решаем эту конструкцию:

В принципе, можно оставить ответ таким, а можно его расписать:

Важные моменты

Такая проблема возникает только тогда, когда речь идет о «некрасивых» аргументах. Когда у нас табличные значения, то ничего такого нет.

Надеюсь, сегодняшний урок помог вам разобраться, что такое метод вспомогательного угла и как его применять на примерах разного уровня сложности. Но это не единственный урок, посвященный решению задач методом вспомогательного угла. Поэтому оставайтесь с нами!

Источник