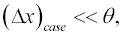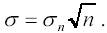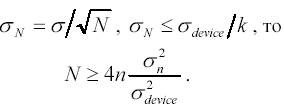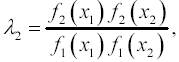Что такое достаточное число измерений
Определение необходимого числа измерений



При планировании эксперимента необходимо помнить, что каждое измерение – это затраты времени и ресурсов (трудовых, материальных, финансовых). В определении числа измерений надо учитывать следующие аспекты:
1. Возможность пренебрежения коэффициентом Стьюдентав вычислении погрешностей измерений. Согласно данным таблицы 2, это можно сделать при более чем 7–10 измерениях при уровне доверительной вероятности α = 0,68 (который используется по умолчанию) и при более чем 15–20 измерениях при уровне доверительной вероятности α = 0,95.
2. Окончательный результат многократного измерения содержит в себе как лучайную, так и приборную погрешности. Поскольку случайная погрешность уменьшается с увеличением количества измерений как 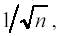
т.е. чтобы случайной погрешностью можно было пренебречьпо сравнению с приборной погрешностью θ.
Поскольку 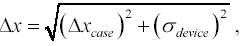
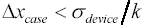
ний, и получена погрешность измерений n σ (число измерений таково, что мы пренебрегли коэффициентом Стьюдента). Погрешность отдельного измерения можно оценить как
Для минимизации числа измерений используется последовательный анализ, т.е. такой способ статистической проверки гипотез, при котором необходимое число наблюдений
не фиксируется заранее, а определяется в процессе самой проверки. Во многих случаях для получения столь же обоснованных выводов применение надлежащим образом подобранного способа последовательного анализа позволяет ограничиться значительно меньшим числом наблюдений (в среднем, т.к. число наблюдений при последовательном анализе есть величина случайная), чем при способах, в которых число наблюдений фиксировано заранее.
Пусть задача состоит в выборе между гипотезами H1 и H2 по результатам независимых наблюдений. Гипотеза H1 заключается в том, что случайная величина Х имеет распределение вероятностей с плотностью f1(x), гипотеза H2 — в том, что Х имеет плотность f2(x). Для решения этой задачи поступают следующим образом. Выбирают два числа А и В
где x2 — результат второго наблюдения, и т.д. С вероятностью, равной единице, процесс оканчивается либо выбором H1, либо выбором H2. Величины А и В определяются из условия, чтобы вероятности ошибок первого и второго рода(т. е. вероятность отвергнуть гипотезу H1, когда она верна, и вероятность принять H1, когда верна H2) имели заданные значения α1 и α2. Более подробную информацию можно найти в учебниках по математической статистике.
3.6. Определение необходимого количества измерений
Увеличение количества измерений (числа проб, образцов и т.п., как видно из выражений (3.18), (3.21) даже при неизменной их точности (sx=const, Sx=const) может увеличить надежность доверительной оценки (P) или сузить доверительный интервал для определения действительного значения измеряемой величины (математического ожидания) d.
Необходимое количество измерений (образцов, проб и т.п.) n для достижения требуемой точности d и заданной надежности Р можно определить заранее в том случае, когда известно действительное значение среднеквадратичного отклонения sx, а экспериментальные данные (измерения) подчиняются нормальному закону распределения.
Действительно, при этих допущениях число измерений можно определить из выражения (3.18)

Таким образом, число измерений n определяется требуемой надежностью Р (доверительной вероятностью a) и относительным (по отношению к среднеквадратичному отклонению) значением доверительного интервала (sx/d), т.е. требуемой точностью определения измеряемой величины. Так при Р=0,95, e(a)=1,96 и при d=sx число измерений равно 4. При увеличении необходимой точности измерений в 2 раза, т.е. сужении доверительного интервала до величины d=(1/2)sx, необходимое число измерений составит 16. Нетрудно заметить, что необходимое число измерений с увеличением точности возрастает в квадратичной зависимости.
Как правило, действительное значение среднеквадратичной ошибки (sx) неизвестно, а имеется только ее оценка (Sx). В этом случае следует воспользоваться соотношением (3.21), т.е. критерием Стьюдента. Необходимое число измерений следует определять из следующего соотношения

При расчетах по этому уравнению следует иметь в виду, что теоретическое значение критерия Стьюдента зависит не только от доверительной вероятности a, но и числа степеней свободы m, последние же определяются числом измерений. В связи с этим уравнение (3.38) следует решать методом последовательных приближений.
В качестве начального приближения можно задать, в частности, число измерений, рассчитанных по формуле (3.37). Так, если решить последнее уравнение методом последовательных приближений, то можно показать, что при P=0,95 (a=0,05) для определения доверительного интервала с точностью d=Sx требуется 7 измерений, а с точностью d=0,5Sx – 19. С повышением необходимой точности различие в числе измерений, рассчитанных по соотношениям (3.37) и (3.38) уменьшается и, как показывают расчеты, при величине d£0,2Sx они практически совпадают.
| Таблица 3.4 Необходимое количество измерений |
| d/Sx | P=0,90 | P=0,95 | P=0,99 |
| 1 | 5 | 7 (4) | 11 |
| 0,5 | 13 | 19 (16) | 31 |
| 0,4 | 19 | 27 (24) | 46 |
| 0,3 | 32 | 46 (48) | 78 |
| 0,1 | 273 | 387 (384) | 668 |
В порядке упражнений постарайтесь определить, какое количество проб чугуна следует отобрать, чтобы повысить надежность доверительного интервала содержания кремния в чугуне до 0,99 и понизить до 0,90? Какое количество проб следует отобрать, чтобы при той же надежности повысить точность (сократить доверительный интервал) определения содержания кремния в чугуне в два раза? Необходимое количество измерений при различных значениях величины доверительного интервала d/Sx и d/sx (в скобках) приведено в табл. 3.4.
Определение минимального количества измерений
Для проведения опытов с заданной точностью и достоверностью необходимо знать то количество измерений, при котором экспериментатор уверен в положительном исходе. В связи с этим одной из первоочередных задач при статических методах оценки является установление минимального, достаточного числа измерений для данных условий. Задача сводится к установлению минимального объема выборки (числа измерений) Nmin при заданных значениях доверительного интервала 2m и доверительной вероятности. При выполнении измерений необходимо знать их точность:


где s0 – среднеарифметическое значение среднеквадратичного отклонения s.
В исследованиях часто по заданной точности D и доверительной вероятности измерения определяют минимальное количество измерений, гарантирующих требуемые значения D и рд.
Аналогично уравнению (8.3) с учетом (8.5) можно получить
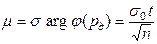
При Nmin=n получаем
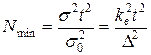
здесь kв – коэффициент вариации (изменчивости), %; D – точность измерений, %.
Для определения Nmin может быть принята такая последовательность вычислений:
1. проводится предварительный эксперимент с количеством измерений п, которое составляет в зависимости от трудоемкости опыта от 20 до 50;
2. вычисляется среднеквадратичное отклонение s по формуле (8.1);
3. в соответствии с поставленными задачами эксперимента устанавливается требуемая точность измерений D, которая не должна превышать точности прибора;
4. устанавливается нормированное отклонение t, значение которого обычно задается (зависит также от точности метода);
5. по формуле (8.7) определяют Nmin и тогда в дальнейшем в процессе эксперимента число измерений не должно быть меньше Nmin..
Для малой выборки доверительный интервал
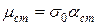
где acт – коэффициент Стьюдента, принимаемый по табл. 10.2 в зависимости от значения доверительной вероятности рд.
Зная mст, можно вычислить действительное значение изучаемой величины для малой выборки
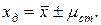
Определение минимального количества измерений



Для проведения опытов с заданной точностью и достоверностью необходимо знать то количество измерений, при котором можно быть уверенным в положительном исходе. В связи с этим, одной из задач является установление минимального, но достаточного числа замеров для данных условий. Задача сводится к установлению минимального объема выборки (числа измерений) nmin при заданных значениях доверительного интервала ± m и доверительной вероятности Рд. При выполнении измерений точность составляет:
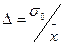
Доверительный интервал для среднего арифметического значения определяется подобно доверительному интервалу для измеренных значений.
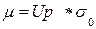
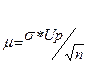 (14) (14) |
С учетом (8) получаем
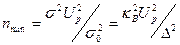
Для определения nmin может быть принята такая последовательность вычислений:
1) проводится предварительный эксперимент с количеством измерений п, которое составляет от 20 до 50;
2) вычисляется упо формуле (6) и
4) задается уровень доверительной вероятности Рд,
5) по формуле (15) определяется птin и в дальнейшем при проведении эксперимента число измерений не должно быть меньше nmin.
Пример: пусть, требуется проверить какой либо параметр, согласно инструкции выполняется 25 замеров, допустимое отклонение параметра ∆=±0,1мм, доверительная вероятность Рд=0,9, вычисленное предварительно значение у=±0,4мм уо=±0,08мм.
Из формулы (15) можно записать .Up = √n*∆/d= √25*0.1/0.4= 1,25.
Из таблицы 1 доверительная вероятность для Up =1,25 составляет 0,79, при заданной Рд=0,9, что недостаточно.
По формуле (15) определим n min = 0,4 2 *1,65 2 /0,08 2 =68 замеров.
Следовательно, для заданных условий необходимо провести не менее 68 замеров.
Значение измеряемой величины, которое в дальнейшем
принимается за расчетнoе, определяется по выражению
Определение необходимого числа измерений
2. Определение необходимого числа измерений.
Дорога 2-й категории, модуль упругости грунта III
Необходимое минимальное достаточное число измерений
t – нормированное отклонение
Kb – коэффициент вариации
Нормированное отклонение (t) – 1,65
Выбираем 25 случайных чисел и наносим их на схему участка измерений, затем для сокращения в объёме работ из них выберем 5 и найдём их координаты.
56; 46; 8; 53; 32; 94; 37; 76; 78; 02; 69; 18; 60; 33; 93; 42; 50; 29; 92; 24; 88; 95; 55; 84; 3.
Вывод: для контроля поперечного уклона на автомобильной дороге 2-й категории необходимо провести 25 измерений. Схема участка измерения представлена на рис.1. Координаты точек измерений следующие:
2.1. Определение основных статистических характеристик выборки.
2.1.2. Среднее арифметическое значение
2.1.3. Среднее квадратичное отклонение
2.1.5. Коэффициент вариации
0,1644>0,15 – неоднородная выборка
2.2. Определение основных статистических характеристик выборки.
2.2.2. Среднее арифметическое значение
2.2.3. Среднее квадратичное отклонение
2.2.5. Коэффициент вариации
2.4. Определение абсолютной и относительной погрешностей выборки. Оценка влияния числа измерений на точность определения статистических характеристик.
Вывод: При выборке N=10 среднеарифметическое значение имеет низкую погрешность, остальные значения погрешностей достаточно высоки (более 5%). При выборке N=5 среднеарифметическое значение также имеет низкую погрешность, остальные значения погрешностей высоки (более 50%), а дисперсия более 100%. В целом, можно заключить, что при N=10 меньших процент погрешностей, чем при N=5.
Учитывая вышеизложенное, можно сказать, что с увеличением числа измерений точность определения характеристик возрастает, как следствие, погрешности уменьшаются.
Контрольная карта N = 5
Контрольная карта N = 10
Контрольная карта N = 20
3. Интервальная оценка параметров распределения.
1. Определить границы доверительного интервала для единичного результата измерения по формуле для N = 20 для всех уровней Pдов.
3. Определить границы доверительного интервала для истинного значения
для N=20; 10; 5 для всех уровней Pдов.
4. Графически изобразить интервалы для N=20; 10; 5 при Pдов. = 0,9
Вывод: С уменьшением количества измерений границы доверительного интервала раздвигаются (для истинного значения случайной величины).