Что такое две смежные вершины
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
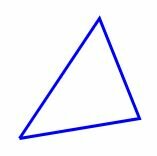 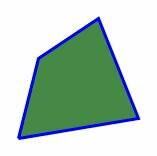 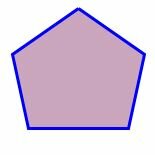  |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
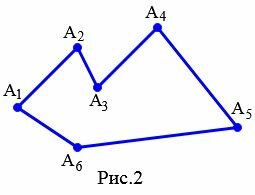 |
На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
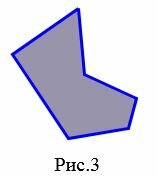 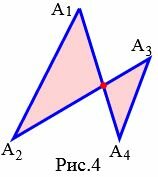 |
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
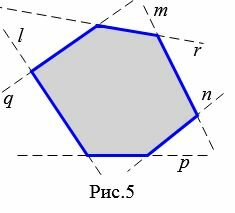 |
На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
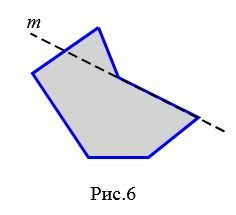 |
На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
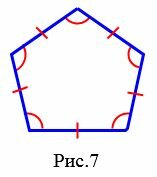 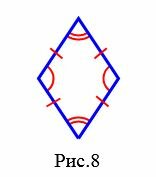 |
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
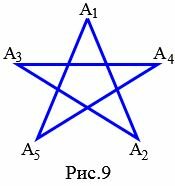 |
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
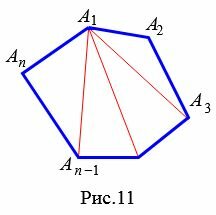 |
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
Параллелограмм: свойства и признаки
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Теория Графов. Часть 2 Смежность, инцидентность, петли
Ничего не сделано, если что-то осталось недоделанным. – Иоганн Гаусс
Смежность и инцидентность
Смежность и инцидентность
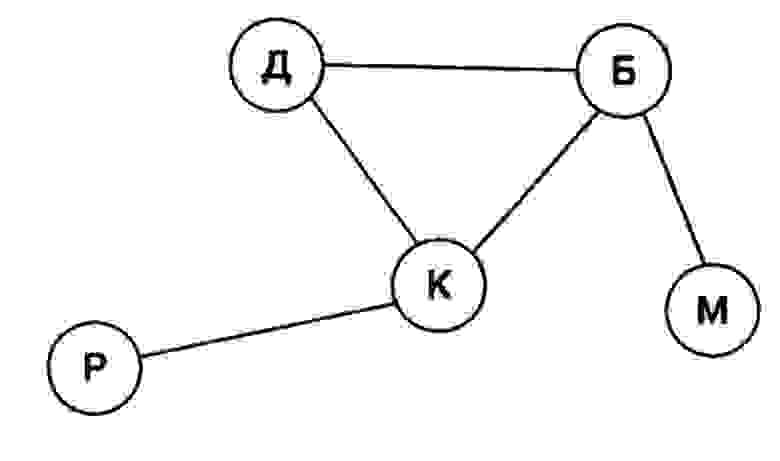
Давайте рассмотрим самый обыкновенный неориентированный граф (Рисунок 1). В нем есть вершина Р и вершина К. Данные вершины являются смежными (adjacent), так как они соединены ребром РК.
Помимо этого, как мы видим, вершина К является концом ребра РК, а Р его началом, в таких случаях вершина К и Р называются инцидентными (incident) ребру РК.
Смежностью вершин графа – называется отношение между двумя вершинами, в котором существует ребро их соединяющее.
Инцидентность – это когда вершина a является началом или концом ребра t. Если мы добавим еще одну вершину b, то мы скажем, что вершина a и b инцидента ребру t.
Кроме вершин, смежность присутствует и у рёбер. Рёбра просто должны иметь общую вершину. В нашем случаи мы можем сказать, что ребро ДК является смежным ребру РК, так как у них есть общая вершина К.
Смежностью рёбер графа – называется отношение между двумя рёбрами, в котором существует вершина соединяющая их.
В связи с тем, что выше мы рассматривали неориентированный граф, то было неважно, с какого направления определять смежность и инцидентность. Вершина Р могла быть смежна вершине К, но также мы могли сказать, что вершина К смежна вершине Р.
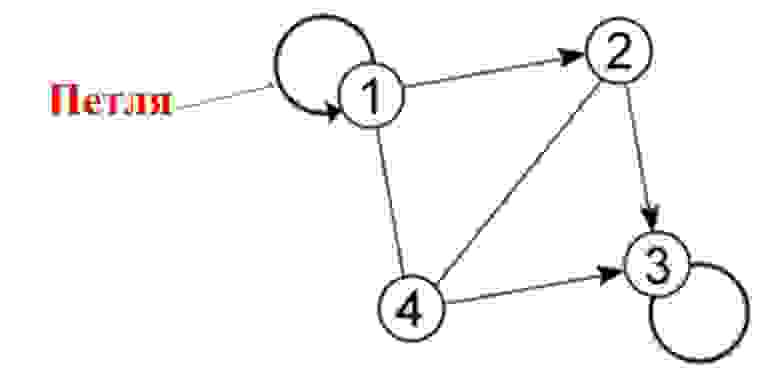
В ориентированном графе все немного по-другому (Рисунок 2), так у нас имеется направление, которое мы не в силах поменять. Если вершина 1 смежна вершине 2, то вершина 2 не может быть смежна вершине 1. То же самое касается и инцидентности. Вершины 1 и 2 инцидентны ребру 12, наоборот не работает.

Петли
Петля – это ребро инцидентное одной и той же вершине. То есть вершина которая соединена сама с собой. На рисунке ниже мы видим, как это выглядит.
Заключение
В следующей статье я покажу, как с помощью матрицы задавать графы, а также покажу, что такое вес ребра.
Ключевые термины
Дата добавления: 2015-06-12 ; просмотров: 7196 ; Нарушение авторских прав
Вес (длина) ребра – это число или несколько чисел, которые интерпретируются по отношению к ребру как длина, пропускная способность.
Вес вершины – это число (действительное, целое или рациональное), поставленное в соответствие данной вершине.
Взвешенный граф – это граф, каждому ребру которого поставлен в соответствие его вес.
Граф – это совокупность двух конечных множеств: множества точек и множества линий, попарно соединяющих некоторые из этих точек.
Вершины (узлы) графа – это множество точек, составляющих граф.
Замкнутый маршрут – это маршрут в графе, у которого начальная и конечная вершины совпадают.
Кратные ребра – это ребра, соединяющие одну и ту же пару вершин.
Маршрут в графе – это конечная чередующаяся последовательность смежных вершин и ребер, соединяющих эти вершины.
Матрица инцидентности – это двумерный массив, в котором указываются связи между инцидентными элементами графа (ребро и вершина).
Матрица смежности – это двумерный массив, значения элементов которого характеризуются смежностью вершин графа
Мультиграф – это граф, у которого любые две вершины соединены более чем одним ребром.
Неориентированный граф (неорграф) – это граф, у которого все ребра неориентированы, то есть ребрам которого не задано направление.
Обход графа (поиск на графе) – это процесс систематического просмотра всех ребер или вершин графа с целью отыскания ребер или вершин, удовлетворяющих некоторому условию.
Ориентированный граф (орграф) – это граф, у которого все ребра ориентированы, то есть ребрам которого присвоено направление.
Открытый маршрут – это маршрут в графе, у которого начальная и конечная вершины различны.
Петля – это ребро, соединяющее вершину саму с собой.
Поиск в глубину – это обход графа по возможным путям, когда нужно сначала полностью исследовать одну ветку и только потом переходить к другим веткам (если они останутся нерассмотренными).
Поиск в ширину – это обход графа по возможным путям, когда после посещения вершины, посещаются все соседние с ней вершины.
Простой граф – это граф, в котором нет ни петель, ни кратных ребер.
Путь – это открытая цепь, у которой все вершины различны.
Ребра (дуги) графа – это множество линий, соединяющих вершины графа.
Связный граф – это граф, у которого для любой пары вершин существует соединяющий их путь.
Смежные вершины – это вершины, соединенные общим ребром.
Смешанный граф – это граф, содержащий как ориентированные, так и неориентированные ребра.
Список ребер – это множество, образованное парами смежных вершин
Тупик – это вершина графа, для которой все смежные с ней вершины уже посещены
Цепь – это маршрут в графе, у которого все ребра различны.
Цикл – это замкнутая цепь, у которой различны все ее вершины, за исключением концевых.
Не нашли то, что искали? Google вам в помощь!
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Реализация графа через смежные вершины
Я начала разбираться но я все равно не могу найти толковый материал. Что нашла (смогла) написила. теперь хочу попросить Вас в помощи. Можете дать ссылку на исходник чтобы можно было посмотреть как на самом деле реализованы эти функции. или если код есть в книгах буду благодарна. А то я уже 2 неделю не могу ничего толкового найти.
Спасибо.
То что у меня есть:
struct Node
<
int mEnd;
float mWeight;
>;
class Graph
<
public:
Graph(int key, bool digraph);
void insert(int key);
void insertEdge(Edge edge);
void remove(int key);
void removeEdge(Edge edge);
bool relatedEdge(Edge edge1, Edge edge2);
int V();
int E();
bool directed();
private:
int Vcnt;
int Ecnt;
bool mDigraph = false;
std::vector > adjacencyLists;
Graph::Graph(int key, bool digraph)
: Vcnt(key)
, Ecnt(0)
, mDigraph(digraph)
, adjacencyLists(key)
<
adjacencyLists.assign(key, 0);
>
void Graph::insert(int key)
<
>
void Graph::insertEdge(Edge edge)
<
int v = edge.mV;
int w = edge.mW;
adjacencyLists[v] = new Node(w, adjacencyLists[v]);
if (!mDigraph)
adjacencyLists[w] = new Node(v, adjacencyLists[w]);
Ecnt++;
>
void Graph::remove(int key)
<
>
void Graph::removeEdge(Edge edge)
<
>
bool Graph::directed()
<
return mDigraph;
>
Последний раз редактировалось martaOlegovna 22.03.2018, 10:17, всего редактировалось 2 раз(а).
#pragma once
#include
struct Edge
<
int mV;
int mW;
>;
struct Node
<
int mEnd;
float mWeight;
>;
using AjacencyList = std::vector ;
class Graph
<
public:
Graph(int key, bool digraph);
void insert(int key);
void insertEdge(Edge edge);
void remove(int key);
void removeEdge(Edge edge);
bool relatedEdge(Edge edge1, Edge edge2);
bool directed();
private:
bool mDigraph = false;
AjacencyList mAdjacencyLists;
>;
#include «stdafx.h»
#include «Graph.h»
#include
Graph::Graph(int key, bool digraph)
: mDigraph(digraph)
, mAdjacencyLists(key)
<
>
void Graph::insert(int key)
<
if (mAdjacencyListsЧто такое две смежные вершины.mEnd == false)
mAdjacencyListsЧто такое две смежные вершины.mEnd = true;
else
std::cout rockclimber
| Заслуженный участник |
Последний раз редактировалось martaOlegovna 22.03.2018, 11:31, всего редактировалось 1 раз.
| Заслуженный участник |
Последний раз редактировалось slavav 22.03.2018, 11:56, всего редактировалось 1 раз.
Я прочитал ваш код. Всё очень плохо. Вы сравниваете переменные типа int и float с константами true и false. Например вес ребра. Из такого кода невозможно понять как вы собираетесь работать с данными.
Пожалуйста, вернитесь на шаг назад: опишите структуру данных словами или псевдокодом. Опишите операции над структурой данных. Участники форума вам помогут сделать описания корректными. Затем можно будет перейти к реализации на C++.
Начнём с начала: что такое представление графа в виде списков смежности?
Последний раз редактировалось martaOlegovna 22.03.2018, 12:10, всего редактировалось 4 раз(а).
Я прочитал ваш код. Всё очень плохо. Вы сравниваете переменные типа int и float с константами true и false. Например вес ребра. Из такого кода невозможно понять как вы собираетесь работать с данными.
Пожалуйста, вернитесь на шаг назад: опишите структуру данных словами или псевдокодом. Опишите операции над структурой данных. Участники форума вам помогут сделать описания корректными. Затем можно будет перейти к реализации на C++.
Начнём с начала: что такое представление графа в виде списков смежности?
и как их реализовать я не знаю. если знаете помогите. если просто написали чтобы поспрашивать по теории. так я знаю теорию. но я ж могу вам скинуть с вики и вы так и не узнаете знаю ли я теорию или нет)
НО как я думаю: Список смежных вершин представляет собой контейнер, каждый элемент которого является списком (vector) номеров вершин
| Заслуженный участник |
1) направленый
2) float mWeight;
struct Edge
<
Edge(int v, int w, float weight);
int mV;
int mW;
float mWeight;
>;
struct Node
<
int mEnd;
float mWeight;
>;
| Заслуженный участник |
Edge::Edge(int v, int w, float weight)
: mV(v)
, mW(w)
, mWeight(weight)
<
>
bool Graph::removeEdge(const Edge& edge)
<
int v = edge.mV;
int w = edge.mW;
auto ita = find_if(mVertexList[edge.mV].cbegin(), mVertexList[edge.mV].cend(), [w](const Node& n) < return n.mEnd == w; >);
mVertexList[edge.mV].erase(ita);
auto itb = find_if(mVertexList[edge.mW].cbegin(), mVertexList[edge.mW].cend(), [v](const Node& n) < return n.mEnd == v; >);
mVertexList[edge.mW].erase(itb);
void Graph::print(const Edge & edge)
<
std::cout Pphantom
| Супермодератор |
| i | Форумный движок обеспечивает возможность подсветки кода, этим стоит пользоваться. |

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей



