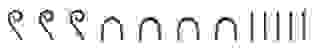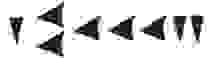Что такое двоичная система счисления в математике
Двоичная система счисления
Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.
Немного истории
Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.
Таблица и алфавит
Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.
1001102 = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 3810
Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:
| Делимое | 38 | 19 | 9 | 4 | 2 |
|---|---|---|---|---|---|
| Делитель | 2 | 2 | 2 | 2 | 2 |
| Частное | 19 | 9 | 4 | 2 | 1 |
| Остаток | 0 | 1 | 1 | 0 | 0 |
Для перевода в другие системы необходимо:
Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:
| Двоичная | Восьмеричная | Шестнадцатеричная |
|---|---|---|
| 0 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | |
| 1001 | 9 | |
| 1010 | A | |
| 1011 | B | |
| 1100 | C | |
| 1101 | D | |
| 1110 | E | |
| 1111 | F |
110010012 = 11 001 001 = 011 001 001 = 3118
110010012 = 1100 1001 = С916
Представление двоичных чисел
В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.
Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.
Прямой код предполагает приписывание единицы в начале без изменений записи:
| A > 0 | Aпр = 0A | 1010112; Aпр = 01010112 |
| A ≤ 0 | Aпр = 1|A| | -1010112; Aпр = 11010112 |
Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:
| A > 0 | Aобр = 0A | 1010112; Aобр = 01010112 |
| A ≤ 0 | Aобр = 1 A | -1010112; Aобр = 10101002 |
Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:
| A > 0 | Aдоп = 0A | 1010112; Aдоп = 01010112 |
| A ≤ 0 | Aдоп = 1 A + 1 | -1010112; Aдоп = 10101012 |
Применение двоичной системы в информатике
Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.
Основы систем счисления
Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палец\зарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:
Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32: 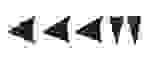
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92: 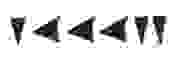
Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа: 
Теперь число 3632 следует записывать, как:
Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Позиционные системы счисления
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.
Десятичная система счисления
Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.
Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*10 2 + 0*10 1 + 3*10 0 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.
Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.
Двоичная система счисления
Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.
Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 510.
Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?
Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.
Восьмеричная система счисления
8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Шестнадцатеричная система счисления
Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.
Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная
Позиционные системы подразделяются на однородные и смешанные.
Однородные позиционные системы счисления
Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.
Смешанные системы счисления
К уже приведенному определению можно добавить теорему: “если P=Q n (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”
Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева
Перевод из одной системы счисления в другую
Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.
Преобразование в десятичную систему счисления
Пример: 1012 = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 510
Преобразование из десятичной системы счисления в другие
Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 1510 = 178.
Преобразование из двоичной в восьмеричную и шестнадцатеричную системы
В качестве примера возьмем число 10012: 10012 = 001 001 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ) = (0+0+1) (0+0+1) = 118
Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.
Преобразование из восьмеричной и шестнадцатеричной систем в двоичную
Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.
Для примера рассмотрим число 458: 45 = (100) (101) = 1001012
Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.
Преобразование дробной части любой системы счисления в десятичную
Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.
Преобразование дробной части двоичной системы в 8- и 16-ую
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.
Пример: 1001,012 = 001 001, 010 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ), (0*2 2 + 1*2 1 + 0*2 0 ) = (0+0+1) (0+0+1), (0+2+0) = 11,28
Преобразование дробной части десятичной системы в любую другую
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Для примера переведем 10,62510 в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,62510 = (1010), (101) = 1010,1012
Криптография: как компьютер считает и кодирует информацию
Как компьютер считает
Когда в древности люди только изобретали счёт, они, как сейчас маленькие дети, считали на пальцах. Пальцев на руках – десять, поэтому и система счисления у нас – десятичная. Однако наша система счёта компьютеру не слишком-то понятна: ему ближе двоичная. У компьютера нет десяти пальцев, но, с другой стороны, и двух тоже нет. Откуда тогда взялась двоичная система, что это за ноль и единица, которыми думает компьютер? И как из них получаются обычные, понятные цифры?
Для того чтобы в общих чертах понять, как думает компьютер, начнём с самого начала. Компьютер, по сути, – это много всякой электроники, собранной вместе в правильном порядке. А электроника (до того, как к ней добавили программу) понимает только одно: включена она или выключена, есть сигнал или нет сигнала.
Обычно «есть сигнал» обозначают единицей, а «нет сигнала» – нулём: отсюда и выражение, что «компьютер говорит на языке нулей и единиц».
Этот язык нулей и единиц называют ещё двоичной системой счисления – потому что в ней всего две цифры. Наша привычная система счисления – десятичная, в ней десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Но есть и множество других – восьмеричная, пятеричная, одиннадцатиричная и какая угодно ещё.
У нас с вами нет цифры «десять», правда? Число 10 состоит из двух цифр – 1 и 0.
Точно так же в пятеричной системе счисления не будет цифры «5», только 0, 1, 2, 3 и 4.
Посчитаем в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42, 43, 44, 100 (. ), 101, 102 и так далее. Можно сказать, что как система счисления называется, такой цифры в ней и нет. В нашей десятичной нет цифры «10», в пятеричной нет цифры «5» (и всех, которые после неё), в восьмеричной – «8» и так далее.
А в шестнадцатиричной «16», например, есть! Поэтому нам шестнадцатиричную систему понять ещё сложнее. Давайте посчитаем в шестнадцатиричной:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22…97, 98, 99, 9A, 9B, 9C, 9D, 9E, 9F, A0, A1, A2… F7, F8, F9, FA, FB, FC, FD, FE, FF, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 10A, 10B, 10C и так далее.
Двоичная система счисления, впрочем, тоже выглядит странновато для непривычного взгляда:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001…
Вот примерно такими числами и думает компьютер где-то внутри себя. Но человеку такими числами думать совершенно неудобно, поэтому мы преобразуем числа из двоичной в более удобную систему счисления.
В компьютерных программах часто используют восьмеричную и шестнадцатиричную системы: компьютеру легко их понять (потому что 8=2*2*2, 16=2*2*2*2, а с двоичной системой компьютер знаком изначально), а для людей это удобно, потому что поближе к привычной десятичной.
Как переводить числа из одной системы счисления в другую
Чтобы понять принцип, будем, как мы с вами любим, разбираться на конфетах.
И на конфетах мы с вами будем переводить число 33 в восьмеричную систему счисления. Мы решим, что единицы – это сами конфеты, а десятки – это коробки, в каждой из которых лежит по десять конфет. Вот и получится, что 33 – это 3 коробки по 10 конфет и ещё 3 конфеты где-то сбоку.
Но мы переводим наше конфетное богатство в восьмеричную систему счисления, а это значит, что нам надо вытряхнуть все конфеты из коробочек по 10, сложить в коробочки по 8 и посмотреть, что из этого выйдет.
Из 33 получится 4 полных восьмеричных коробочки и 1 конфета останется сама по себе, так как 33/8=4 (ост. 1). То есть 33=8*4+1 – так в восьмеричной системе счисления получается число 41.
33 в десятичной – это 41 в восьмеричной. Это одно и то же число, просто разложенное по разным коробочкам, переведённое в разное основание. Количество конфет не поменялось, мы просто считали их по-разному!
Двоичная система, как мы уже выяснили, более странная и непривычная для человеческого взгляда. Давайте попробуем перевести 33 в двоичную – получится аж 16 коробочек по 2! И что же делать? Писать 16 как-то странно, помня о том, что в двоичной системе есть только ноль и единица, а шестёрки, которая нам нужна для шестнадцати, совершенно точно нет!
Посмотрим на нашу десятичную систему. В ней мы считаем десятки – 10, 20, 30, 40, 50, 60, 70, 80, 90 – а когда у нас набирается десять десятков, мы достаём большую коробку – 100.
У нас 100 – это 10*10, 1000 – 10*10*10, 10 000 – 10*10*10*10 и так далее. Для других систем счисления это работает точно так же! В восьмеричной системе 100=8*8, 1000=8*8*8; в двоичной 100=2*2, а 1000=2*2*2; а в шестнадцатиричной (есть и такая, помните?) 100=16*16, 1000=16*16*16.
Здесь нам пригодятся степени. Если вы их ещё не проходили в школе, не пугайтесь, степени – это очень просто. Число в степени – это число, сколько-то раз умноженное на само себя. То есть 5 3 =5*5*5 (пять в третьей степени – это пять, три раза умноженная сама на себя: 5*5*5), или 8 5 =8*8*8*8*8 (восемь в пятой степени – это восемь, пять раз умноженная на саму себя: 8*8*8*8*8).
Если мы вспомним про наши 10 000=10*10*10*10 в десятичной и 1000=8*8*8 в восьмеричной, то можно легко заметить, что сколько нулей, столько раз и умножаем на само себя. Другими словами, количество символов в числе минус один – это степень, в которую надо возвести основание. В числе 1000 у нас четыре символа, значит умножать надо 4–1, то есть 3 раза. Если основание 10, то тысяча – это 10, три раза умноженная сама на себя: 10*10*10. Если основание 8, то тысяча – это 8, три раза умноженная сама на себя: 8*8*8.
Обо всём этом мы заговорили, пытаясь перевести 33 в двоичную систему. Просто так поделить это число на коробочки по 2 оказалось затруднительным. Но если вспомнить про наши сотни-тысячи, можно задуматься: а ведь в двоичной 100=2*2, 1000=2*2*2, 10 000=2*2*2*2 и так далее.
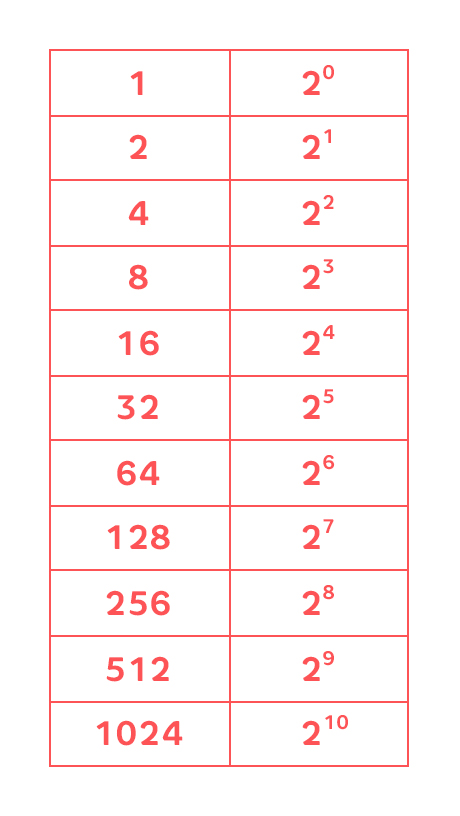
Для перевода из десятичной системы в двоичную удобно помнить степени двойки. Даже можно сказать, что без этой хитрости со степенями мы устанем, умаемся и немножко сойдем с ума. А степени двойки выглядят как-то так:
Теперь, глядя на табличку, мы видим, что 33=2 5 +1, то есть 33=2*2*2*2*2+1. Вспоминаем – сколько раз умножаем, столько будет нулей – то есть наше 2*2*2*2*2 в двоичной системе будет 100000. Не забудем оставшуюся в стороне единичку, и получится, что 33 в десятичной – это 100001 в двоичной. Правильно и красиво это записывают так:
Давайте (чтобы совсем хорошо понять) переведём в двоичную систему число 15.
г) Три минус два – осталась 1 конфета, тут уже табличка не понадобится. В таблички такого рода можно не смотреть, когда ваш остаток меньше основания, а наша единица точно меньше двойки.
Когда просто смотришь на все эти шаги, кажется, что это просто свалка из Кучи Разных Странно Написанных Цифр. И запутаться во всём этом в первый раз – нормально. И во второй, и в третий. Просто попробуйте сделать это ещё и ещё раз – по шагам, как написано выше, и всё получится.
И наоборот это тоже работает! Например, число 110101012 – как из него сделать понятное десятичное? Точно так же, при помощи таблички. Пойдем с конца:
1*2 0 +0*2 1 +1*2 2 +0*2 3 +1*2 4 +0*2 5 +1*2 6 +1*2 7 =
Вот примерно так компьютер понимает привычные нам числа.
Когда смотришь на это в первый раз, кажется, что это, во-первых, совершенно непостижимо, а, во-вторых, вообще не сработает. Поэтому сейчас мы с вами сделаем немножко математической магии, чтобы убедиться, что системы счисления – это такая же реальная вещь, как, например, задача «раздать пятерым детям пятнадцать печенек поровну».
Итак, возьмем пример 15+6 и решим его в разных системах счисления. Понятно, что в нашей, десятичной, получится 21. А что выйдет, например, в восьмеричной?
Переводим 15 в восьмеричную систему счисления. Первый шаг у нас при переводе в другую систему – посмотреть в табличку степеней. 8 2 – это уже 64, и в 15 оно точно уже никак не влезет, поэтому берем 8 1 – то есть просто 8. 15–8=7, оно меньше нашего основания 8, поэтому с ним мы ничего не делаем.
Итак, получилось, что 15=8 1 +7.
В восьмеричной системе логика точно такая же, как, например, в двоичной: 8 3 – это 1000, 8 2 – это 100, 8 1 – это 10. Получилось, что:
Напомню, наш пример был 15+6. 15 мы перевели в восьмеричную систему, как же перевести 6? Она меньше 8, нашего основания, поэтому ответ – оставить как есть. Наш пример сейчас выглядит так:
Теперь мы будем складывать в восьмеричной системе счисления. Как это делается? Так же, как и в десятичной, но надо помнить, что десяток в восьмеричной системе – это восемь, а не десять, и что 8 и 9 в ней не существует.
Когда мы считаем в десятичной системе, по сути, мы делаем так:
15+6=15+5+1=20+1=21
Попробуем проделать тот же фокус в восьмеричной системе:
Почему 17+1? Потому что 7+1=8, а 8 – это наш десяток! В восьмеричной системе 7+1=10, а значит, 17+1=20. Если на этом месте ваш мозг начинает бить тревогу и рассказывать, что здесь что-то не так, вернитесь в начало статьи, где мы с вами считали в разных системах счисления.
Теперь наш пример выглядит как
Переведем 258 обратно в нашу систему счисления. В десятичной мы бы, увидев число 25, могли сказать, что в нём две десятки и пять единиц. В восьмеричной, как вы, наверное, уже догадались, число 258 – это две восьмерки и пять единиц. То есть 258=2*8+5=2110.
Итак, наш пример целиком:
Получилось точно такое же 21, какое вышло у нас в самом начале, когда мы посчитали 15+6 привычным нам способом в десятичной системе.
Арифметические правила не меняются от того, что мы выбрали другую систему счисления. Поэтому и компьютер, переводя всё в нули и единицы, которые для нас выглядят непонятно и бессмысленно, не теряет при этом информацию, которую мы ему дали, и может, посчитав в удобной ему форме, выдать результат, переведя его обратно в привычный нам вид.
Мини-курсы для родителей
Рекомендации экспертов и разборы реальных ситуаций
Кодирование информации в информатике
Мы обсуждили, как компьютер понимает числа. Они получаются из других чисел – двоичных, которые компьютер понимает. А как быть с буквами? Картинками? Играми?
Какие вообще бывают виды кодирования информации в науке обращения с компьютером – информатике?
Тут надо на секунду задуматься, как общаются сами люди. Мы используем слова, из слов делаем предложения, из предложений – текст, рассказ, диалог. Но чтобы сделать слово, мы используем буквы, которых всего-навсего 33 штуки!
Просто представьте: все книги, которые вы когда-либо читали – это лишь разные сочетания одних и тех же 33 букв.
Но мы делаем из букв слова по определённым правилам, а словами обозначаем предметы, свойства, действия, эмоции, фантазии. Буквы – это кубики, из которых мы строим слова. А слова – это код, которым мы обозначаем всё, что встречается в нашей жизни, чтобы потом об этом кому-нибудь рассказать.
Точно так же происходит и с компьютером. При помощи цифр мы объясняем компьютеру, что у него есть монитор, мышка, клавиатура и другие детали, рассказываем, как с ними обращаться и как реагировать, когда что-то делаем мы.
Но сейчас мы с вами поговорим о более конкретных и практических кодах. И начнём с того, как компьютер понимает буквы.
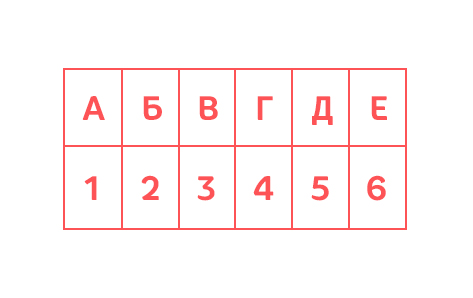
Раз компьютер знает только цифры, значит и буквы он видит через цифры. Это, примерно, как если бы мы букву А записали как 1, Б как 2, В как 3, и так далее.
Примерно такие таблицы (только больше и сложнее) компьютер и использует, чтобы понимать буквы.
Представьте себе: кто-то записал анекдот на компьютер и прислал вам. Вы открываете документ, а там ничего непонятно. Примерно вот так:
ЧеДовек сейчас увидит Дишь то, что ожидает увидеть.
Это компьютер ошибся с кодировкой. Что такое кодирование в информатике? Так обычно называют присвоение каждому символу (букве, знакам препинания и так далее) определённого кода согласно специальной табличке. Кодировка – это способ, которым зашифровывает и расшифровывает буквы компьютер, можно сказать, табличка, которую он выбирает. Табличек у него на такой случай много, и надо знать, по какой расшифровывать, иначе получится белиберда.
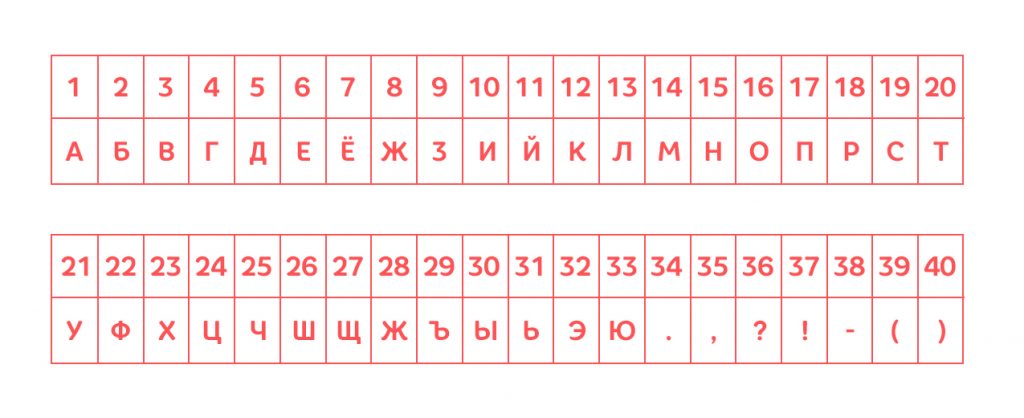
Давайте немножко побудем компьютером. У нас с вами будет две таблички: в одной сначала будет идти алфавит, а потом знаки препинания, в другой – наоборот.
Кодировочная Таблица 1:
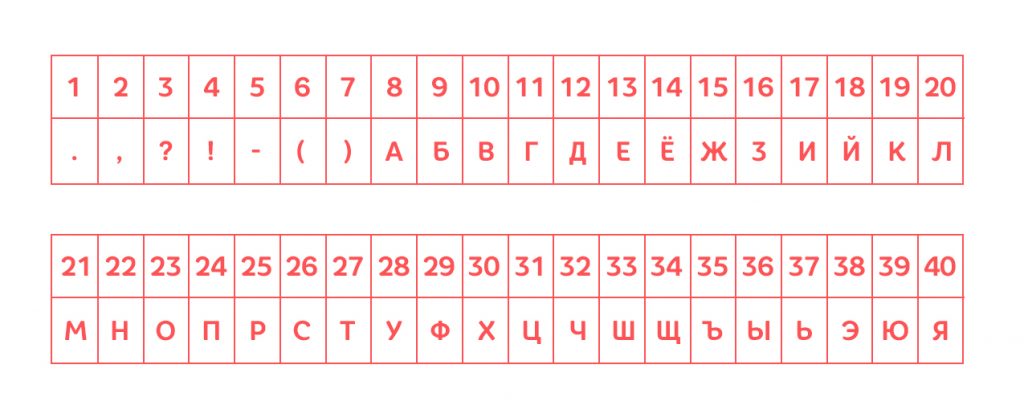
Кодировочная Таблица 2:
Зашифруем с вами фразу «Пароль – три зелёных свистка». Зашифровывать мы будем по первой таблице, а расшифровывать – по второй.
Первая буква – П. В первой таблице у неё номер 17. Дальше буква А. У неё номер 1. Продолжите сами и проверьте себя, правильно ли у вас получится!
А получилась в итоге вот такая строчка:
17-1-18-16-13-30 38 20-18-10 9-6-13-6-15-29-23 19-3-10-19-20-12-1
Теперь попробуем расшифровать её при помощи второй таблицы.
Во второй таблице цифра 17 у буквы И, цифра 1 у точки и так далее (расшифруйте сами).
И.йзех э лйв(жфо к?вклд
Итак, результат, во-первых, непонятный, а, во-вторых, совершенно не похож на ту фразу, которую мы хотели передать. И получилось это из-за того, что таблица для шифровки и таблица для дешифровки не совпали.
Точно так же с фразой и с текстом вроде «Р§РµР”РѕРІРµРє сейчас» – так получается, когда компьютер пытается расшифровать текст не по той таблице, по которой он был зашифрован. Ещё в таких случаях говорят, что «в тексте неправильная кодировка». Сам текст от этого не испортился, просто программе где-нибудь в настройках надо указать, какой кодировкой воспользоваться (обычно это utf8, или UNICODE, или как в этом случае Windows-1251).
Давным-давно, когда компьютеры были большими, а жёсткие диски в них –маленькими, придумали кодировку ASCII (читается как «аскИ»).
Это табличка, где зашифрованы буквы латинского алфавита (мы обычно привыкли о них думать, как об английских буквах), знаки препинания и некоторые служебные символы (например, символ, который обозначает, что надо продолжить с нового абзаца).
Когда в компьютерах придумывают что-то новое, однажды бывает очень важно, чтобы кто-то сказал: «А теперь ВОТ ЭТО мы все делаем одинаково». Например, весь вай-фай в мире работает примерно одинаково, поэтому почти любой телефон может подключиться почти к любой точке вай-фай.
Точно так же произошло и с кодировочной таблицей. Мы с вами раньше уже убедились, что она обязательно должна быть одинаковая у отправителя и получателя, и этой одинаковой таблицей стала ASCII аж в 1963 году.
Сначала всё было замечательно, но потом компьютеры стали становиться меньше и удобнее, ими стали пользоваться разные люди, в том числе не знающие английского. А русский, например, алфавит (который также называют «кириллица») в ASCII не входит. Как быть? Куда бежать? И в 1991 году был придуман UNICODE (читается как «Юникод» или «Уникод» – почти как «Универмаг», но не магазин).
Юникод может закодировать очень большое число символов из разных письменностей: китайские иероглифы, математические символы, буквы греческого алфавита, латиницы и кириллицы.
ASCII стала первой частью Юникода, и специальные договоренности в программах позволяют читать при помощи Юникода текст, который был закодирован в ASCII.
Когда вы сохраняете файл в том же «Блокноте», вы можете выбрать кодировку и при выборе заметить, что их гораздо больше, чем мы разобрали в статье.
В заключение давайте поговорим, где какая кодировка нужна.
Обычно выбором кодировки занимаются люди, работающие с компьютерами профессионально – при написании программ, настройки баз данных и т. п. Мы с вами не будем вникать во все тонкости, и рассмотрим этот вопрос в общих чертах:
– Windows-1251
Как видно из названия, это основная кодировка операционных систем семьи Windows. Когда вы точно знаете, что все компьютеры, которые будут работать с файлами, используют Windows – она отличный выбор. Если же нет, могут возникнуть проблемы с невидимыми символами. Потому что Windows-1251 их считает служебными, а многие другие кодировки решают, что это такие буквы непонятные, и в результате случается неразбериха.
– ASCII
Старая, но надёжная. Подойдёт, если ваш текст на английском, а компьютер, где надо открыть файл – очень, очень старый.
– UNICODE
Это рекомендуемая кодировка для всех систем! Если друг прислал вам файл, а у вас в нём кракозябры, попросите его пересохранить файл с кодировкой unicode, и, скорее всего, проблема будет решена.
– UTF-8
Вариант записи того же Юникода. Он специфический, и обычно используется программами при общении внутри себя самих (например, общение программы со своей базой данных).
Итак, кодированием текста в информатике обычно называют способ компьютера перевести текст в понятный ему вид по одной из общепринятых табличек. Если файл был сохранён в одной кодировке, а открыт в другой – обычно получается белиберда вместо текста.
Все компьютеры знают одни и те же кодировки, чтобы понимать файлы, сделанные другими компьютерами, но кодировки существуют разные – под разные цели. Лучше всего сохранять файлы в кодировке UNICODE – так больше всего шансов, что у другого человека этот файл откроется.
Как можно увидеть, криптография – это не только наука про тайны и не только детская игра. У этой науки есть множество простых практических точек приложения, и если ребёнок знаком с её концепциями, то многое, что может испугать, сбить с толку и привести в отчаяние, для него будет просто задачей, к которой надо найти правильное решение.
Мини-курсы для родителей от 199 руб.
Рекомендации, разборы ситуаций и проверенные практики от экспертов