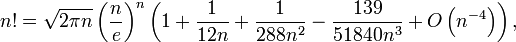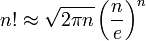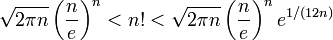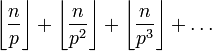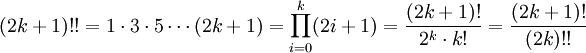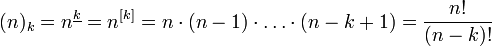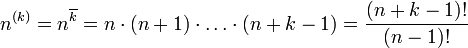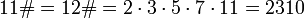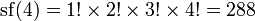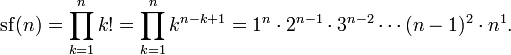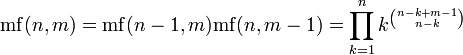Что такое двойной факториал
Двойной факториал
Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:
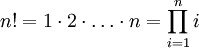
Иногда словом «факториал» неформально называют восклицательный знак.
Содержание
Свойства
Комбинаторное определение
В комбинаторике факториал определяется как количество перестановок множества из n элементов. Например, элементы множества <A,B,C,D> можно линейно упорядочить 4!=24 способами:
Связь с гамма-функцией
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при 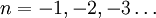
Формула Стирлинга
Формула Стирлинга — асимптотическая формула для вычисления факториала:
см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).
Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые в степени
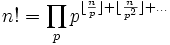
где произведение берется по всем простым числам.
Другие свойства
Обобщения
Двойной факториал
Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,
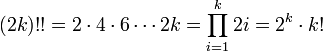
Убывающий факториал
Убывающим факториалом (или неполным факториалом) называется выражение
Убывающий факториал дает число размещений из n по k.
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Примориал (англ. Primorial ) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,
Последовательность праймориалов начинается так:
2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)
Суперфакториалы
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)
Последовательность суперфакториалов начинается (с n = 0 ) с
1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)
Идея была обобщена в 2000 Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial ), которые являются произведением первых n суперфакториалов. Первые члены (с n = 0 ) равны:
1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)
где 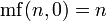
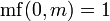
Субфакториал
Субфакториал 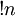
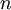
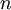
Ссылки
См. также
Полезное
Смотреть что такое «Двойной факториал» в других словарях:
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
Двойной крестик — Одинарный и двойной крестики разными шрифтами Типографский крестик (†, в Юникоде U+2020, в dagger;), иногда его называют «кинжалом», «обелиском», «даггером», типографический знак. Двойной крестик (‡, в Юникоде U+2021, в Dagger;) вариант «кинжала… … Википедия
Список интегралов от экспоненциальных функций — Ниже приведён список интегралов (первообразных функций) от экспоненциальной функции. Для более полного списка интегралов смотрите таблицу интегралов и другие списки интегралов. Заметим, что везде опущена аддитивная константа интегрирования. для … Википедия
Гиперсфера — Стереографическая проекция поверхности 3 сферы на трёхмерное пространство. На рисунке изображены три координатных направления на 3 сфере: параллели (красный), меридианы (синий) и гипермеридианы (зелёный). В исход … Википедия
Эллиптический интеграл — В интегральном исчислении, эллиптический интеграл появился в связи с задачей вычисления длины дуги эллипса и был впервые исследован Джулио Фаньяно и Леонардом Эйлером. В современном представлении, эллиптический интеграл это некоторая… … Википедия
Tcl — Запрос «TCL» перенаправляется сюда; о минидистрибутиве Linux см. Tiny Core Linux. Tcl Семантика: императивный … Википедия
TCL — Семантика: императивный, скриптовый Тип исполнения: интерпретатор Появился в: 1988 г. Автор(ы): Джон Остераут Последняя версия: 8.5.7 / 15 апреля 2009 … Википедия
Для четного n двойной факториал равен
а для нечетных n это
Термин нечетный факториал иногда используется для двойного факториала нечетного числа.
СОДЕРЖАНИЕ
История и использование
В статье 1902 года физик Артур Шустер писал:
Отношение к факториалу
Факториал ненулевого n может быть записан как произведение двух двойных факториалов:
где знаменатель отменяет нежелательные множители в числителе. (Последняя форма также применяется при n = 0. )
Для четного неотрицательного целого числа n = 2 k с k ≥ 0 двойной факториал может быть выражен как
Приложения в перечислительной комбинаторике
Двойные факториалы мотивированы тем фактом, что они часто встречаются в перечислительной комбинаторике и других условиях. Например, n ‼ для нечетных значений n отсчетов
Четные двойные факториалы дают номера элементов гипероктаэдрических групп (перестановки со знаком или симметрии гиперкуба )
Расширения
Отрицательные аргументы
Сложные аргументы
Отсюда можно вывести альтернативное определение z ‼ для неотрицательных четных целых значений z :
со значением 0‼ в этом случае
Дополнительные удостоверения
Используя вместо этого расширение двойного факториала нечетных чисел до комплексных чисел, формула
Двойные факториалы также могут использоваться для вычисления интегралов от более сложных тригонометрических полиномов.
Двойные факториалы нечетных чисел связаны с гамма-функцией тождеством:
Некоторые дополнительные тождества, включающие двойные факториалы нечетных чисел:
Приближение для отношения двойного факториала двух последовательных целых чисел:
Обобщения
Определения
Альтернативное расширение многофакторной
Обобщенные числа Стирлинга, расширяющие многофакторные функции
Класс обобщенных чисел Стирлинга первого рода определяется при α > 0 следующим треугольным рекуррентным соотношением:
Точные конечные суммы с участием нескольких факториальных функций
и, кроме того, у нас аналогично есть разложения этих функций в двойную сумму, заданные формулой
Что такое двойной факториал
В комбинаторике факториал определяется как количество перестановок множества из n элементов. Например, элементы множества можно линейно упорядочить 4!=24 способами:
Связь с гамма-функцией
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при 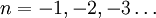
Формула Стирлинга
Формула Стирлинга — асимптотическая формула для вычисления факториала:
см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).
Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые в степени
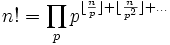
где произведение берется по всем простым числам.
Другие свойства
Обобщения
Двойной факториал
Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,
Убывающий факториал
Убывающим факториалом (или неполным факториалом) называется выражение
Убывающий факториал дает число размещений из n по k.
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Примориал (англ. Primorial ) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,
Последовательность праймориалов начинается так:
2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)
Суперфакториалы
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)
Последовательность суперфакториалов начинается (с n = 0 ) с
1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)
Идея была обобщена в 2000 Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial ), которые являются произведением первых n суперфакториалов. Первые члены (с n = 0 ) равны:
1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)
где 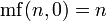
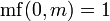
Субфакториал
Субфакториал 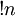
Ссылки
См. также
Смотреть что такое «Двойной факториал» в других словарях:
Факториал — числа n (лат. factorialis действующий, производящий умножающий; обозначается n!, произносится эн факториал) произведение всех натуральных чисел от 1 до n включительно … Википедия
Двойной крестик — Одинарный и двойной крестики разными шрифтами Типографский крестик (†, в Юникоде U+2020, в dagger;), иногда его называют «кинжалом», «обелиском», «даггером», типографический знак. Двойной крестик (‡, в Юникоде U+2021, в Dagger;) вариант «кинжала… … Википедия
Список интегралов от экспоненциальных функций — Ниже приведён список интегралов (первообразных функций) от экспоненциальной функции. Для более полного списка интегралов смотрите таблицу интегралов и другие списки интегралов. Заметим, что везде опущена аддитивная константа интегрирования. для … Википедия
Гиперсфера — Стереографическая проекция поверхности 3 сферы на трёхмерное пространство. На рисунке изображены три координатных направления на 3 сфере: параллели (красный), меридианы (синий) и гипермеридианы (зелёный). В исход … Википедия
Эллиптический интеграл — В интегральном исчислении, эллиптический интеграл появился в связи с задачей вычисления длины дуги эллипса и был впервые исследован Джулио Фаньяно и Леонардом Эйлером. В современном представлении, эллиптический интеграл это некоторая… … Википедия
Tcl — Запрос «TCL» перенаправляется сюда; о минидистрибутиве Linux см. Tiny Core Linux. Tcl Семантика: императивный … Википедия
TCL — Семантика: императивный, скриптовый Тип исполнения: интерпретатор Появился в: 1988 г. Автор(ы): Джон Остераут Последняя версия: 8.5.7 / 15 апреля 2009 … Википедия
Примеры:
Для четного n двойной факториал равен:
Для нечетного n двойной факториал равен:
Рекомендуется: Пожалуйста, сначала попробуйте подход , прежде чем переходить к решению.
Рекурсивное решение:
Двойной факториал можно рассчитать по следующей рекурсивной формуле.
Ниже приводится реализация двойного факториала.
ссылка на сайт
brightness_4
= «edit-on- > код
Джава
ссылка на сайт
brightness_4
код
python3
ссылка на сайт
brightness_4
код
ссылка на сайт
brightness_4
код
ссылка на сайт
brightness_4
код
Итеративное решение:
Двойной факториал также может быть вычислен итеративно, поскольку рекурсия может быть дорогостоящей для больших чисел.
ссылка на сайт
brightness_4
код
Джава
ссылка на сайт
brightness_4
код
python3
ссылка на сайт
brightness_4
код
ссылка на сайт
brightness_4
код
ссылка на сайт
brightness_4
код
Временная сложность указанных решений составляет O (n).
Важные моменты :
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.
Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

По определению полагают 
Последовательность факториалов неотрицательных целых чисел начинается так:
1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, … (последовательность A000142 в OEIS)
Содержание
Свойства
Рекуррентная формула
Комбинаторная интерпретация
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества из 4-х элементов существует 4! = 24 перестановки:
Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, т. к. пустое множество упорядочено единственным способом.
Связь с гамма-функцией
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.
Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при 
Формула Стирлинга
см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).
Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Разложение на простые числа
Каждое простое число p входит в разложение 
где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.
Другие свойства
Обобщения
Двойной факториал
Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,
По определению полагают 
Последовательность значений n!! начинается так:
1, 1, 2, 3, 8, 15, 48, 105, 384, 945, … (последовательность A006882 в OEIS)
Кратный факториал
m-кратный факториал числа n обозначается 
Пусть число n представимо в виде 


Двойной факториал является частным случаем m-кратного факториала для m = 2.
Связь с гамма-функцией
Убывающий факториал
Убывающим факториалом (или неполным факториалом) называется выражение
Убывающий факториал даёт число размещений из n по k.
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Праймориал или примориал (англ. primorial ) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,
Последовательность праймориалов (включая 
1, 2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)
Суперфакториалы
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых 
Последовательность суперфакториалов чисел n⩾0 начинается так:
1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)
Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial ), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0 начинается так:
1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)
Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал числа n как произведение первых n (m-1)-уровневых факториалов, то есть
где 

Субфакториал
Субфакториал