Что такое результат измерения

результат измерения

3.5 результат измерения: Значение параметра, полученное после проведения измерения.

2.4.13 результат измерения : Значение величины или оценка свойства, полученное(ая) путем измерений.

3.15 результат измерения: Значение величины, найденной путем ее измерения.

5.1.7 результат измерения (measured value): Оцененное значение характеристики качества воздуха, полученное на основе выходного сигнала и обычно включающее в себя результаты вычислений, связанных с процессом калибровки и пересчетом к требуемым величинам.

3.1.21 результат измерения : Значение величины, найденное путем ее измерения.

Смотри также родственные термины:

результат измерения физической величины; результат измерения; результат: Значение величины, полученное путем ее измерения.

[Рекомендации по межгосударственной стандартизации [1], статья 8.1]

Полезное

Смотреть что такое «результат измерения» в других словарях:

результат измерения — matavimo rezultatas statusas T sritis Standartizacija ir metrologija apibrėžtis Matavimo būdu rasta matuojamojo dydžio vertė. atitikmenys: angl. measurement result; result of a measurement vok. Messergebnis, n rus. результат измерения, m pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

результат измерения — matavimo rezultatas statusas T sritis fizika atitikmenys: angl. measurement result; result of measurement vok. Meßergebnis, n; Meßresultat, n rus. результат измерения, m pranc. résultat de mesure, m … Fizikos terminų žodynas

результат измерения физической величины; результат измерения; результат — результат измерения физической величины; результат измерения; результат: Значение величины, полученное путем ее измерения. [Рекомендации по межгосударственной стандартизации [1], статья 8.1] Источник … Словарь-справочник терминов нормативно-технической документации

результат измерения физической величины — результат измерения результат Значение величины, полученное путем ее измерения. [РМГ 29 99] Тематики метрология, основные понятия Синонимы результатрезультат измерения EN result of a measurement DE Messergebnis FR résultat d un mesurage … Справочник технического переводчика

результат измерения дымности в режиме свободного ускорения — ХМ, м 1 Среднеарифметическое значение четырех последних измерений ХМ, полученных в соответствии с 5.4.1 и 5.4.2. [ГОСТ Р 52160 2003] Тематики автотранспортная техника … Справочник технического переводчика

результат измерения, выполненного при возникновении события — [Интент] Тематики релейная защита EN measured event data … Справочник технического переводчика

результат измерения, выполненного при наступлении какого-либо события — [Интент] Тематики релейная защита EN measured event value … Справочник технического переводчика

результат измерения дымности в режиме свободного ускорения — 3.10 результат измерения дымности в режиме свободного ускорения Xср, м 1: Среднеарифметическое значение четырех последних измерений Хм, полученных в соответствии с 5.4.1 и 5.4.2. Источник … Словарь-справочник терминов нормативно-технической документации

Результат измерения физической величины — Значение величины, полученное путем ее измерения. Источник: Государственная система обеспечения единства измерения. Метрология. Основные термины и определения. РМГ 29 99 (введены Постановлением Госстандарта РФ от 17.05.2000 N 139 ст) … Официальная терминология

Результат измерения исправленный — Полученное при измерении значение величины и уточненное путем введения в него необходимых поправок на действие систематических погрешностей. Источник: Государственная система обеспечения единства измерения. Метрология. Основные термины и… … Официальная терминология

Источник

РЕЗУЛЬТАТ ИЗМЕРЕНИЙ И ЕГО ХАРАКТЕРИСТИКИ

Понятие «результат измерений» также не имеет однозначного определения. Одни авторы считают, что результатом измерения является значение величины плюс оценка погрешности измерения, другие полагают, что результат измерения — это значение величины, найденное путем ее измерения. Последнее положение закреплено ГОСТ 16263-70. В международных словарях, толкования этого понятия близки друг другу и практически совпадают с определением, приведенным в ГОСТ 16263-70. Очевидно, при выборе определения данного понятия следует исходить из того, что на практике большинство измерений являются однократными, поэтому за их результат нередко принимается то значение величины, которое непосредственно снято с прибора, — без обработки и оценивания погрешности, так как в этом нет необходимости. Например, токарь, обрабатывая деталь, периодически, в целях контроля, выполняет однократные измерения какого-либо ее параметра при помощи штангенциркуля. На основании результатов этих измерений он принимает решение о дальнейшей обработке детали. Оператор в котельной, основываясь на показаниях манометра (в данном случае — это результаты измерений) и сравнивая их с заданными значениями давления, принимает решение о регулировании режима сгорания топлива. Из этого следует, что результатом измерения является именно значение величины, которое удалось получить при помощи того или иного средства измерений. Но это вовсе не означает, что погрешности результатов данного вида измерений неизвестны. Они регламентируются заранее (до выполнения измерений) выбором необходимых по точности средств измерений.

Примеры. Оператор снял показание щитового амперметра — 100 А, т. е. произвел отсчет. Этот отсчет и есть результат измерения R, т. е. R = отсчету.

При измерении длины отрезка I при помощи штрихового метра с микроскопами произведены два отсчета, соответствующие концам отрезка: О₁ = 11,1 мм и О₂ = 85,6 мм. Разность отсчетов О₂ — О₁ = 74,5 мм будет результатом измерения отрезка I, т. е. R = О₂ — О₁.

При измерении массы m вещества на весах выполнено пять равноточных измерений: m_1, m_2, m_3, m₄ и m₅ соответственно равных 5,5; 5,6; 5,5; 5,4 и 5,5 мг. В этом случае за результат многократного измерения принимают среднее арифметическое из пяти значений: m = 5,5 мг, т. е.

(1.1)

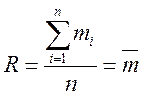
При неравноточных измерениях результатом многократного измерения является среднее взвешенное. В таком случае,

(1.2)

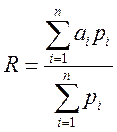
где a_i—значение величины, полученное из i-го измерения, входящего в ряд неравноточных измерений; p_i — вес і-го измерения данного ряда (определение веса измерений приведено ниже).

Часто в полученный результат измерений вводят поправки. В итоге значение величины до и после введения поправки будет различным. Это должно найти отражение в терминологии.

Неисправленный результат измерения (кратко — неисправленный результат) — значение физической величины, полученное при помощи средства измерений до введения поправок.

Исправленный результат измерения (кратко — исправленный результат) — значение физической величины, полученное при помощи средства измерений и уточненное путем введения в него необходимых поправок.

Автоматические средства измерений высокой точности, сопряженные с ЭВМ, выполняют измерения и обработку данных. Результатом обработки данных является исправленное значение величины и оценка его погрешности. Что считать результатом измерений в данном случае? Казалось бы, те данные, которые выдает автоматическое средство измерений, и есть результат измерений (значение величины плюс оценка погрешности). Однако это не так. Автоматическое средство измерений одновременно выдает исправленный результат измерений и оценку погрешности результата измерений.

Сходимость результатов измерений (кратко — сходимость измерений) — характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, выполняемых повторно одними и теми же средствами, одним и тем же методом, в одинаковых условиях.

1. Количественную оценку сходимости измерений можно произвести по разностям полученных значений величины или отсчетов показаний. Сходимость измерений двух групп многократных измерений может характеризоваться размахом, средней квадратической или средней арифметической погрешностью.

2. Сходимость результатов измерений может быть также получена по результатам одновременно выполненных измерений одной и той же величины однотипными средствами измерений.

Воспроизводимость результатов измерений (кратко — воспроизводимость измерений) — характеристика качества измерений, отражающая близость друг другу результатов измерений одной и той же величины, полученных в разных местах, разными методами и средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям (температура, давление, влажность и др.).

Примечание. Воспроизводимость измерений может характеризоваться средней квадратической погрешностью сравниваемых групп измерений.

Точность результата измерений (кратко — точность измерений) — характеристика качества измерения, отражающая близость к нулю погрешности его результата (чем меньше погрешность измерения, тем выше его точность).

Правильность результата измерений (кратко — правильность измерений) — характеристика качества измерений, отражающая близость к нулю систематических погрешностей в их результатах.

Примечание. Стандартизованный термин «правильность измерений» в указанном значении не нашел широкого применения. Обычно применительно к конкретной измерительной задаче считают правильным тот результат измерения, погрешность которого не превышает установленного значения.

Среднее взвешенное значение (кратко — среднее взвешенное) — среднее значение величины, полученное на основании ряда неравноточных измерений с учетом весов отдельных результатов, принятых в обработку.

Вес результата измерений (кратко — вес измерений или вес, буквенное обозначение р) — положительное число, служащее оценкой доверия тому или иному отдельному результату измерения, входящему в ряд неравноточных измерений.

Измерительная информация (ИИ) — информация о значениях одной или нескольких физических величин.

1. Измерительная информация может быть представлена в различной форме (именованным числом, словами, в виде кода).

2. Кроме значения величины в ИИ могут включаться данные о погрешности измерений, числе, условиях измерений и другие данные.

Источник

результат измерения физической величины; результат измерения; результат

результат измерения физической величины; результат измерения; результат: Значение величины, полученное путем ее измерения.

[Рекомендации по межгосударственной стандартизации [1], статья 8.1]

Смотреть что такое «результат измерения физической величины; результат измерения; результат» в других словарях:

результат измерения физической величины — результат измерения результат Значение величины, полученное путем ее измерения. [РМГ 29 99] Тематики метрология, основные понятия Синонимы результатрезультат измерения EN result of a measurement DE Messergebnis FR résultat d un mesurage … Справочник технического переводчика

Результат измерения физической величины — Значение величины, полученное путем ее измерения. Источник: Государственная система обеспечения единства измерения. Метрология. Основные термины и определения. РМГ 29 99 (введены Постановлением Госстандарта РФ от 17.05.2000 N 139 ст) … Официальная терминология

результат измерения — 3.5 результат измерения: Значение параметра, полученное после проведения измерения. Источник: ГОСТ Р 52205 2004: Угли каменные. Метод спектрометрического определения генетических и технологических параметров … Словарь-справочник терминов нормативно-технической документации

Результат (точечного) измерения — 7. Результат (точечного) измерения определенное по показанию СИ значение искомой величины в заданной контрольной точке с оценкой неопределенности измерений. Результатом измерения является интервал значений искомой величины от до Rmin до Rmax, в… … Словарь-справочник терминов нормативно-технической документации

ЕДИНИЦЫ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН — величины, по определению считающиеся равными единице при измерении других величин такого же рода. Эталон единицы измерения ее физическая реализация. Так, эталоном единицы измерения метр служит стержень длиной 1 м. В принципе, можно представить… … Энциклопедия Кольера

ГОСТ Р 8.736-2011: Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения — Терминология ГОСТ Р 8.736 2011: Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения оригинал документа: 3.11 грубая погрешность измерения: Погрешность… … Словарь-справочник терминов нормативно-технической документации

Погрешность измерения — Сюда перенаправляется запрос «Относительная точность». На эту тему нужна отдельная статья. Сюда перенаправляется запрос «Абсолютная то … Википедия

Физические величины — Физическая величина это количественная характеристика объекта или явления в физике, либо результат измерения. Размер физической величины количественная определенность физической величины, присущая конкретному материальному объекту, системе,… … Википедия

ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ — измерение электрических величин, таких, как напряжение, сопротивление, сила тока, мощность. Измерения производятся с помощью различных средств измерительных приборов, схем и специальных устройств. Тип измерительного прибора зависит от вида и… … Энциклопедия Кольера

Источник

результат измерений

3.16 результат измерений : Среднее арифметическое значение «n» результатов единичного измерения.

3.2 результат измерений (test result): Значение характеристики, полученное выполнением регламентированного метода измерений.

Такой подход к представлению результатов измерений имеет место в МИ 1317 [2].

3.1.12 результат измерений: Среднеарифметическое значение заданной совокупности измерений.

Смотри также родственные термины:

3.1.2 результат измерений (анализа): Значение массовой доли определяемого элемента (компонента) в пробе, полученное экспериментально-расчетным путем с учетом сравнительных значений (градуировочных зависимостей), выраженное в узаконенных единицах.

Полезное

Смотреть что такое «результат измерений» в других словарях:

результат измерений — Значение характеристики, полученное выполнением регламентированного метода измерений. Примечание. В нормативном документе на метод измерений должно регламентироваться, сколько (одно или несколько) единичных наблюдений должно быть выполнено,… … Справочник технического переводчика

Результат измерений — Значение величины или оценка свойства, полученные путем измерений. Примечания: 1. За результат измерений в шкалах разностей (интервалов), отношений и абсолютных чаще всего принимают среднее арифметическое из ряда результатов равноточных… … Официальная терминология

результат измерений HV — 3.4 результат измерений HV: Медиана (к + 1) е значение среди (2к + 1) значений ряда результатов наблюдений, расположенных в порядке возрастания. Примечание Например, третье из пяти расставленных в порядке возрастания значений чисел HV, полученных … Словарь-справочник терминов нормативно-технической документации

результат измерений числа HSD — 3.3 результат измерений числа HSD: Медиана третье из пяти расставленных в порядке возрастания значений твердости металлов по HSD, полученных при измерениях в пяти точках, расположенных равномерно по рабочим поверхностям меры. Источник … Словарь-справочник терминов нормативно-технической документации

результат измерений (анализа) — 3.1.2 результат измерений (анализа): Значение массовой доли определяемого элемента (компонента) в пробе, полученное экспериментально расчетным путем с учетом сравнительных значений (градуировочных зависимостей), выраженное в узаконенных единицах … Словарь-справочник терминов нормативно-технической документации

исправленный результат измерений величины — 3.3 исправленный результат измерений величины: Результат измерений величины, полученный после введения поправки в целях устранения систематических погрешностей в неисправленный результат измерений величины. Источник … Словарь-справочник терминов нормативно-технической документации

неисправленный результат измерений величины — 3.2 неисправленный результат измерений величины: Результат измерений величины, полученный до введения в него поправки в целях устранения систематических погрешностей. Источник … Словарь-справочник терминов нормативно-технической документации

результат единичного анализа — 3.4 результат единичного анализа (определения)2): Значение содержания компонента в пробе вещества (материала), полученное при однократной реализации процедуры анализа. 1) Результат анализа по сути представляет собой среднее п результатов… … Словарь-справочник терминов нормативно-технической документации

результат единичного анализа (определения) — 3.8. результат единичного анализа (определения): Значение содержания компонента в пробе воды, полученное при однократной реализации процедуры анализа. Источник … Словарь-справочник терминов нормативно-технической документации

Источник

РМГ 29-2013 ГСИ. Метрология. Основные термины и определения

5 Результаты измерений

5.1 результат (измерения величины): Множество значений величины, приписываемых измеряемой величине вместе с любой другой доступной и существенной информацией.

1 Определение понятия результата измерения претерпело существенное изменение по сравнению с определением РМГ 29-99 и вобрало в себя выражение точности измерения. Информация, приводимая в результате измерения, определяется особенностями конкретного измерения и соответствует требованиям, предъявляемым к этому измерению. В большинстве случаев информация относится к точности измерения и выражается показателями точности, в обоснованных случаях содержит указание методики измерений и др.

2 Результат измерения может быть представлен измеренным значением величины с указанием соответствующего показателя точности. К показателям точности относятся, например, среднее квадратическое отклонение, доверительные границы погрешности, стандартная неопределенность измерений, суммарная стандартная и расширенная неопределенности. VIM3 [1] предусматривает также представление результата измерений плотностью распределения вероятностей на множестве возможных значений измеряемой величины.

3 Если значение показателя точности измерений можно считать пренебрежимо малым для заданной цели измерения, то результат измерения может выражаться как одно измеренное значение величины. Во многих областях это является обычным способом выражения результата измерения, с указанием класса точности применяемого средства измерений.

measurement result, result of measurement

5.2 измеренное значение (величины): Значение величины, которое представляет результат измерения.

1 Для измерения, в котором имеют место повторные показания, каждое показание может использоваться, чтобы получить соответствующее измеренное значение величины. Такая совокупность отдельных измеренных значений величины может быть использована для вычисления результирующего измеренного значения величины, такого как среднее арифметическое или медиана, обычно с меньшей соответствующей неопределенностью (погрешностью) измерений.

2 Когда диапазон истинных значений величины, представляющих измеряемую величину, мал по сравнению с неопределенностью (погрешностью) измерений, измеренное значение величины может рассматриваться как оценка, по сути дела, единственного истинного значения величины, и оно часто представляет собой среднее арифметическое или медиану отдельных измеренных значений, которые получены при повторных измерениях.

3 В случае, когда диапазон истинных значений величины, представляющих измеряемую величину, нельзя считать малым по сравнению с неопределенностью (погрешностью) измерений, измеренное значение часто будет оценкой среднего арифметического или медианы набора истинных значений величины.

4 В GUM [3] для понятия измеренное значение величины используют термины результат измерения и оценка значения измеряемой величины или просто оценка измеряемой величины. См. также 5.1, примечание 1.

measured quantity value, measured value of a quantity, measured value

5.3 опорное значение (величины): Значение величины, которое используют в качестве основы для сопоставления со значениями величин того же рода.

1 Опорное значение величины может быть истинным значением величины, подлежащей измерению, в этом случае оно неизвестно, или принятым значением величины, в этом случае оно известно.

2 Опорное значение величины со связанной с ним неопределенностью (погрешностью) измерений обычно приводят для:

— материала, например, аттестованного стандартного образца;

— устройства, например, стабилизированного лазера;

— референтной методики измерений;

reference quantity value, reference value

5.4 истинное значение (величины): Значение величины, которое соответствует определению измеряемой величины.

1 Определение измеряемой величины включает принятие некоторой модели объекта измерения, в которой истинное значение представлено неким параметром. Всегда существует пороговое несоответствие модели и объекта измерения, которое является причиной дефинициальной неопределенности измеряемой величины.

2 Когда дефинициальная неопределенность, связанная с измеряемой величиной, считается пренебрежимо малой по сравнению с остальными составляющими неопределенности измерений, измеряемая величина может рассматриваться как имеющая «по сути единственное» истинное значение. Такой подход принят в GUM [3] и в связанных с ним документах, где слово «истинный» считается излишним.

3 Существуют подходы оценивания точности измерений, которые избегают понятия истинного значения величины и опираются на понятие метрологической совместимости результатов измерения.

true quantity value, true value of a quantity, true value

5.5 принятое значение (величины): Значение величины, по соглашению приписанное величине для данной цели.

1 Иногда принятое значение величины является оценкой истинного значения величины.

2 Неопределенность измерений, связанная с принятым значением часто достаточна мала и может быть принята равной нулю для конкретной цели. В этом случае используют понятие действительное значение величины.

conventional quantity value, conventional value of a quantity, conventional value

5.6 действительное значение (величины): Значение величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.

conventional true value of a quantity

5.7 точность измерений; точность результата измерения: Близость измеренного значения к истинному значению измеряемой величины.

measurement accuracy, accuracy of measurement, accuracy

5.8 правильность (измерений): Близость среднего арифметического бесконечно большого числа повторно измеренных значений величины к опорному значению величины.

1 Правильность измерений не является величиной и поэтому не может быть выражена численно, однако соответствующие показатели приведены в ISO 5725 [4].

2 Правильность измерений отражает близость к нулю систематической погрешности измерений.

measurement trueness, trueness of measurement, trueness

5.9 прецизионность (измерений): Близость между показаниями или измеренными значениями величины, полученными при повторных измерениях для одного и того же или аналогичных объектов при заданных условиях.

1 «Заданные условия» могут быть, например, условиями повторяемости измерений, условиями промежуточной прецизионности измерений или условиями воспроизводимости измерений (см. ISO 5725-1 [4]).

2 Понятие прецизионность измерений используется для определения понятий повторяемости измерений, промежуточной прецизионности измерений и воспроизводимости измерений.

3 Прецизионность измерений характеризует близость к нулю случайной погрешности измерений.

measurement precision, precision

5.10 условия повторяемости (измерений): Один из наборов условий измерений, включающий применение одной и той же методики измерений, того же средства измерений, участие тех же операторов, те же рабочие условия, то же местоположение и выполнение повторных измерений на одном и том же или подобных объектах в течение короткого промежутка времени.

repeatability condition of measurement, repeatability condition

5.11 повторяемость измерений: Прецизионность измерений в условиях повторяемости измерений.

measurement repeatability, repeatability

5.12 условия промежуточной прецизионности (измерений): Один из наборов условий измерений, включающий применение одной и той же методики измерений, то же местоположение и выполнение повторных измерений на одном и том же или аналогичных объектах в течение длительного периода времени, а также может включать другие условия, которые могут изменяться.

1 Изменения могут включать новые калибровки, калибраторы, средства измерений, а также новых операторов.

2 Описание условий должно включать все условия, изменяемые и неизменяемые, насколько это оправдано практически.

intermediate precision condition of measurement, intermediate precision condition

5.13 промежуточная прецизионность (измерений): Прецизионность измерений в фиксированных условиях промежуточной прецизионности измерений.

intermediate measurement precision, intermediate precision

5.14 условия воспроизводимости (измерений): Один из наборов условий измерений, включающий разные местоположения, разные средства измерений, участие разных операторов и выполнение повторных измерений на одном и том же или аналогичных объектах.

1 В исключительных случаях, разные средства измерений могут применяться в соответствии с разными методиками измерений.

2 Описание условий должно включать все условия, изменяемые и неизменяемые, насколько это оправдано практически.

reproducibility condition of measurement, reproducibility condition

5.15 воспроизводимость (измерений): Прецизионность измерений в условиях воспроизводимости измерений.

measurement reproducibility, reproducibility

5.16 погрешность (результата измерения): Разность между измеренным значением величины и опорным значением величины.

1 Если опорное значение величины известно, как, например, при калибровке средств измерений, то известно и значение погрешности измерения. Если в качестве опорного значения выступает истинное значение величины, то значение погрешности неизвестно.

2 В РМГ 29-99 использовался термин погрешность результата измерения: отклонение результата измерения от истинного (действительного) значения измеряемой величины. Изменение термина вызвано изменением понятия результат измерения (см. 5.1, примечание 1).

3 Погрешность измерения равна сумме случайной и систематической погрешностей.

measurement error, error of measurement, error

5.17 случайная погрешность (измерения): Составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных в определенных условиях.

random measurement error, random error of measurement, random error

5.18 среднее квадратическое отклонение; стандартное отклонение: Параметр функции распределения измеренных значений или показаний, характеризующий их рассеивание и равный положительному корню квадратному из дисперсии этого распределения.

1 Оценкой среднего квадратического отклонения является выборочное стандартное отклонение, определяемое по формуле

,

— среднее арифметическое из измеренных значений или показаний.

2 является оценкой стандартного отклонения распределения и называется выборочным стандартным отклонением среднего арифметического.

3 Выборочное стандартное отклонение иногда неправильно называют средняя квадратическая погрешность.

5.19 систематическая погрешность (измерения): Составляющая погрешности измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной и той же величины.

1 В зависимости от характера изменения во времени систематические погрешности подразделяют на постоянные, прогрессирующие, периодические и погрешности, изменяющиеся по сложному закону. В зависимости от характера изменения по диапазону измерений систематические погрешности подразделяются на постоянные и пропорциональные.

Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.

2 Оставшуюся систематическую погрешность измерения после введения поправки называют неисключенной систематической погрешностью (НСП).

3 Для оценки систематической погрешности измерения в VIM3 [1] используется термин смещение (при измерении).

systematic measurement error, systematic error of measurement, systematic error

5.20 поправка: Значение величины, вводимое в показание с целью исключения систематической погрешности.

Компенсация может иметь различные формы, такие как дополнительное слагаемое или множитель, или она может находиться по соответствующей таблице.

5.21 поправочный множитель: Числовой коэффициент, на который умножают показание с целью исключения влияния систематической погрешности.

5.22 доверительные границы (погрешности измерения): Верхняя и нижняя границы интервала, внутри которого с заданной вероятностью находится значение погрешности измерений.

1 Доверительные границы при вероятности, равной 1, называют границами погрешности.

2 Доверительные границы погрешности иногда неправильно называют доверительная погрешность.

5.23 максимальная допускаемая погрешность (измерения): Максимальное значение погрешности измерения (без учета знака), разрешенное спецификацией или нормативными документами для данного измерения.

maximum permissible measurement error, maximum permissible error

5.24 погрешность метода (измерений): Составляющая погрешности измерений, обусловленная несовершенством принятого метода измерений.

5.25 инструментальная погрешность (измерения): Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.

5.26 абсолютная погрешность (измерения): Погрешность измерения, выраженная в единицах измеряемой величины.

absolute error of a measurement

5.27 относительная погрешность (измерения): Погрешность измерения, выраженная отношением абсолютной погрешности измерения к опорному значению измеряемой величины.

или , %,

5.28 модель измерений; уравнение измерений: Уравнение связи между величинами в конкретной измерительной задаче.

measurement model, model of measurement, model

5.29 измерительная информация: Информация о значении величины, входящей в модель измерений.

5.30 функция измерений: Зависимость величин модели измерений, используемая для получения измеренного значения выходной величины по известным значениям входных величин.

5.31 входная величина (в модели измерений): Величина, которая должна быть измерена, или величина, значение которой может быть получено иным способом, для вычисления измеренного значения измеряемой величины.

1 Входная величина в модели измерений часто является выходной величиной средства измерений.

2 Входными величинами в модели измерений могут быть показания, поправки и влияющие величины.

input quantity in a measurement model, input quantity

5.32 выходная величина (в модели измерений): Величина, измеренное значение которой получают, используя значения входных величин в модели измерений.

output quantity in a measurement model, output quantity

5.33 влияющая величина: Величина, которая при прямом измерении не влияет на величину, которую фактически измеряют, но влияет на соотношение между показанием и результатом измерения.

1 Частота при прямом измерении постоянной амплитуды переменного тока с помощью амперметра.

2 Молярная концентрация билирубина при прямом измерении молярной концентрации гемоглобина в плазме крови человека.

3 Температура микрометра, применяемого для измерения длины стержня, но не температура самого стержня, которая может входить в определение измеряемой величины.

4 Фоновое давление в источнике ионов масс-спектрометра во время измерения молярной доли вещества.

1 Косвенное измерение включает комбинацию прямых измерений, каждое из которых может находиться под воздействием влияющих величин.

2 В GUM [3] понятие влияющая величина охватывает не только величины, влияющие на средство измерений, как в определении, приведенном выше, но также и те величины, которые влияют на фактически измеряемые величины. Кроме того, в GUM [3] это понятие не ограничивается прямыми измерениями.

5.34 неопределенность (измерений): Неотрицательный параметр, характеризующий рассеяние значений величины, приписываемых измеряемой величине на основании измерительной информации.

measurement uncertainty, uncertainty of measurement, uncertainty

5.35 стандартная неопределенность (измерений): Неопределенность измерений, выраженная в виде стандартного отклонения.

standard measurement uncertainty, standard uncertainty of measurement, standard uncertainty

5.36 суммарная стандартная неопределенность (измерений): Стандартная неопределенность измерений, которую получают суммированием отдельных стандартных неопределенностей измерений, связанных с входными величинами в модели измерений.

combined standard measurement uncertainty, combined standard uncertainty

5.37 расширенная неопределенность (измерений): Произведение суммарной стандартной неопределенности и коэффициента охвата большего, чем число один.

expanded measurement uncertainty, expanded uncertainty

5.38 интервал охвата: Интервал, основанный на имеющейся информации, который содержит совокупность истинных значений измеряемой величины с заданной вероятностью.

1 Если результат измерения представлен плотностью распределения вероятностей на множестве возможных значений измеряемой величины, то для любого интервала значений может быть вычислена соответствующая вероятность. Наличие плотности распределения вероятностей позволяет для заданной вероятности определить интервал значений измеряемой величины. Таких интервалов существует множество, обычно подразумевают наикратчайший интервал или интервал, симметричный относительно измеренного значения величины.

2 Интервал охвата не следует отождествлять с «доверительным интервалом» во избежание путаницы с этим статистическим понятием.

3 Интервал охвата может быть получен из расширенной неопределенности измерений.

5.39 вероятность охвата: Вероятность того, что совокупность истинных значений измеряемой величины находится в указанном интервале охвата.

5.40 коэффициент охвата: Число, большее чем один, на которое умножают суммарную стандартную неопределенность измерений для получения расширенной неопределенности измерений.

5.41 оценивание (неопределенности измерений) по типу А: Оценивание составляющей неопределенности измерений путем статистического анализа измеренных значений величины, получаемых при определенных условиях измерений.

Type A evaluation of measurement uncertainty, Type A evaluation

5.42 оценивание (неопределенности измерений) по типу В: Оценивание составляющей неопределенности измерений способами, отличными от оценивания неопределенности измерений по типу А.

— связанной со значениями величины, взятыми из авторитетных публикаций;

— связанной со значением аттестованного стандартного образца;

— полученной из сертификатов калибровки;

— связанной с классом точности поверенного средства измерений;

— полученной, исходя из пределов, установленных на основе опыта.

Type В evaluation of measurement uncertainty, Type В evaluation

5.43 бюджет неопределенности: Отчет о неопределенности измерений, составляющих неопределенности, их вычислении и суммировании.

5.44 дефинициальная неопределенность: Составляющая неопределенности измерений, являющаяся результатом ограниченной детализации в определении измеряемой величины.

1 Дефинициальная неопределенность есть практический минимум неопределенности измерений при любом измерении данной величины.

2 Любое изменение детализации в определении величины ведет к другой дефиницальной неопределенности.

5.45 целевая неопределенность (измерений): Верхняя граница неопределенности измерений, заранее установленная, исходя из предполагаемого использования результатов измерений.

target measurement uncertainty, target uncertainty

5.46 относительная стандартная неопределенность измерений: Стандартная неопределенность измерений, деленная на модуль измеренного значения величины.

relative standard measurement uncertainty

5.47 метрологическая совместимость (результатов измерений): Свойство множества результатов измерений для определенной измеряемой величины, при котором абсолютное значение разности любой пары измеренных значений величины, полученное из двух различных результатов измерений, меньше, чем некоторое выбранное кратное стандартной неопределенности измерений этой разности.

metrological compatibility of measurement results, metrological compatibility

Источник