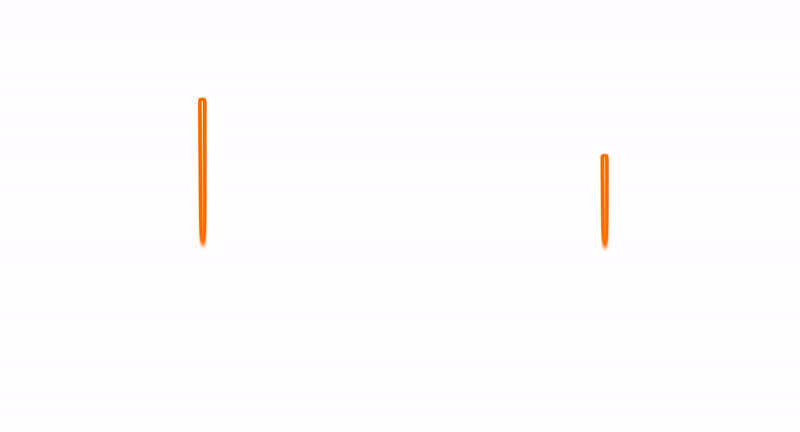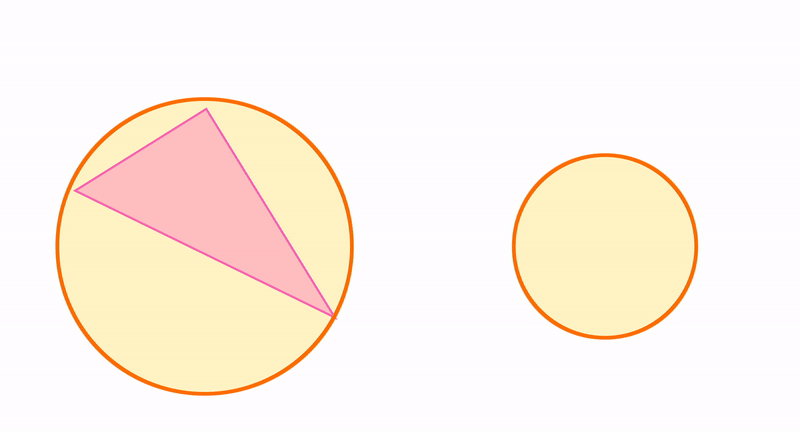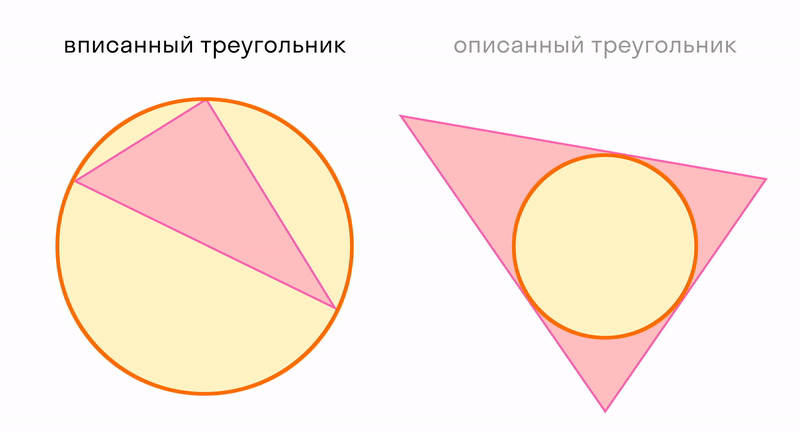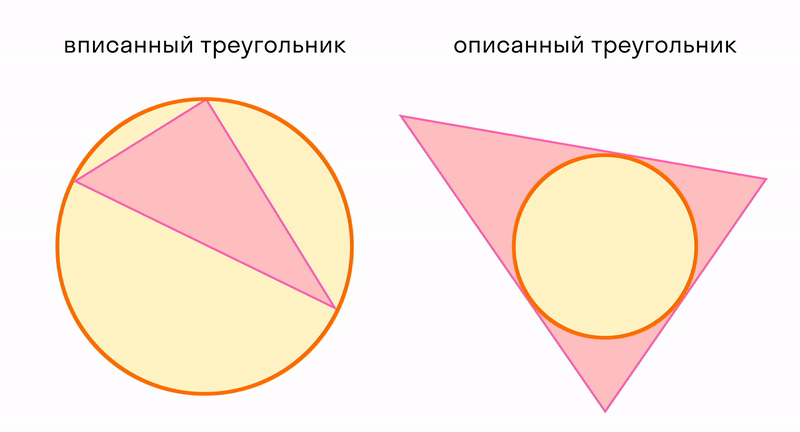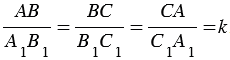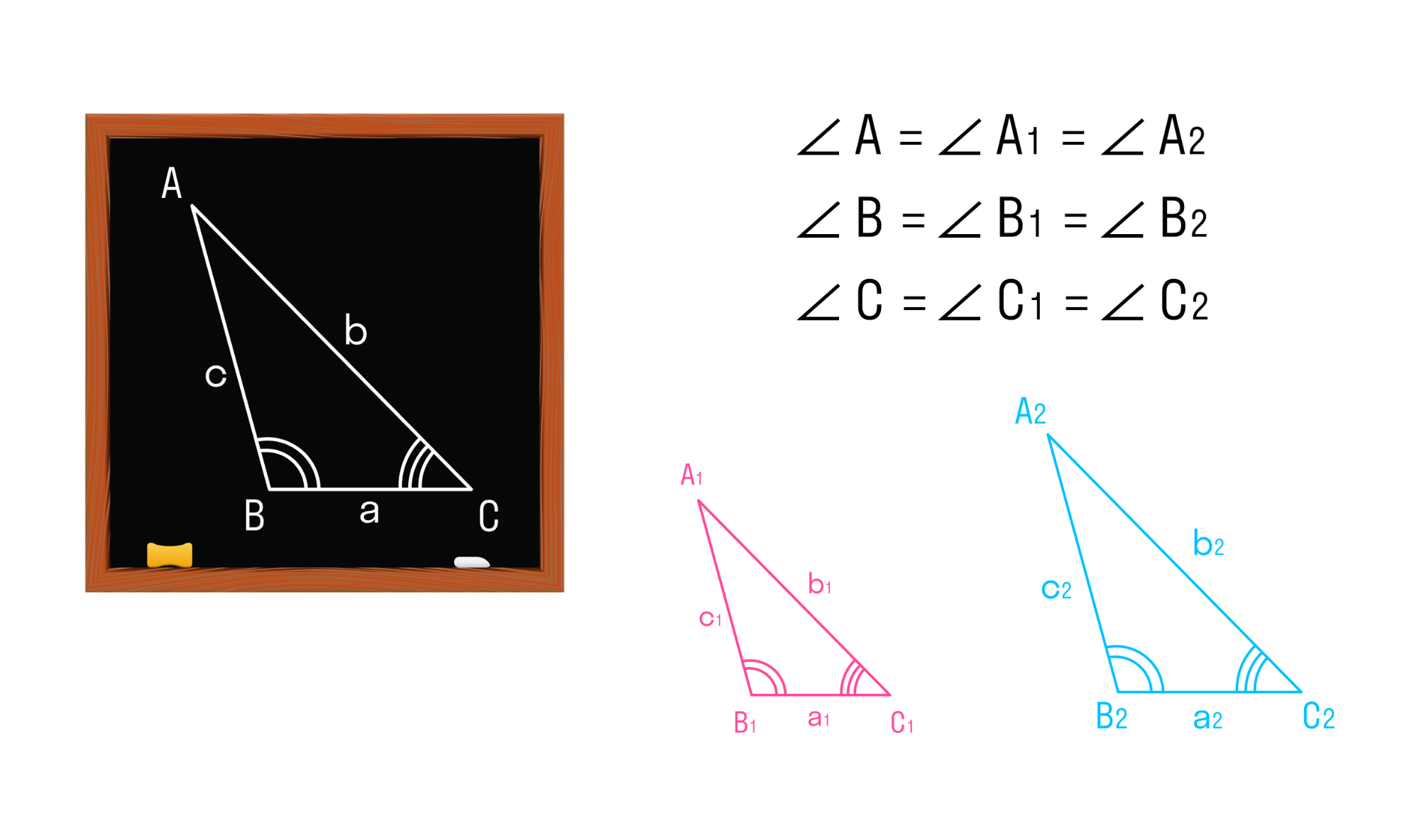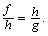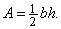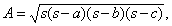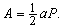Что такое геометрия кратко

Основы геометрии

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.

Все эти фигуры обладают двумя свойствами:

Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.

У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.

Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).

Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.

Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.

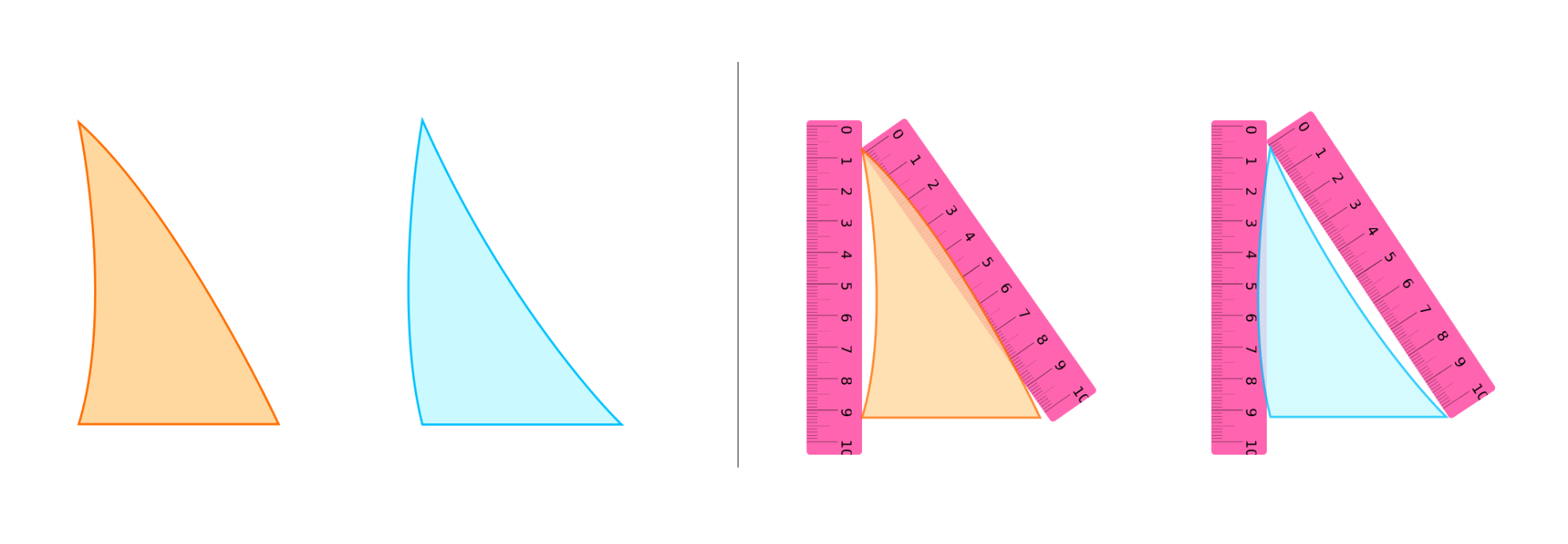
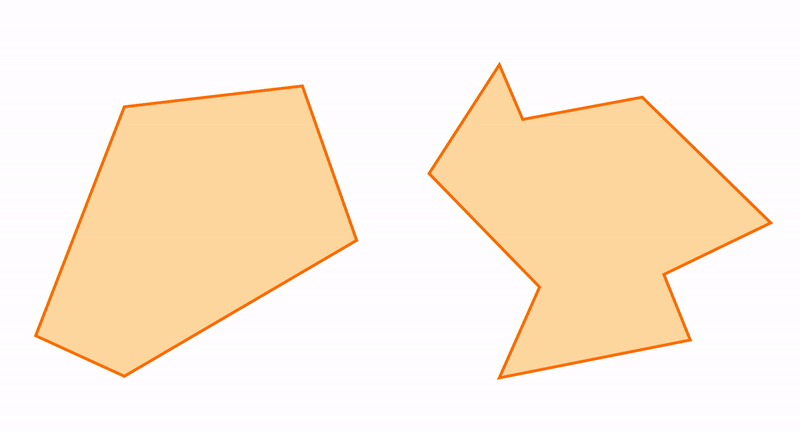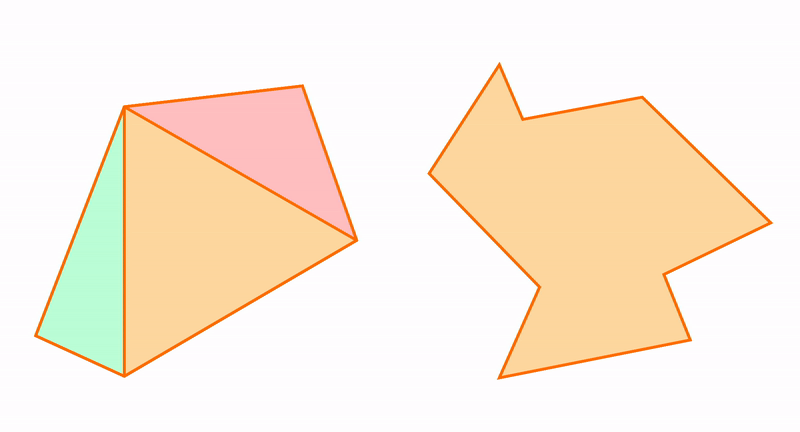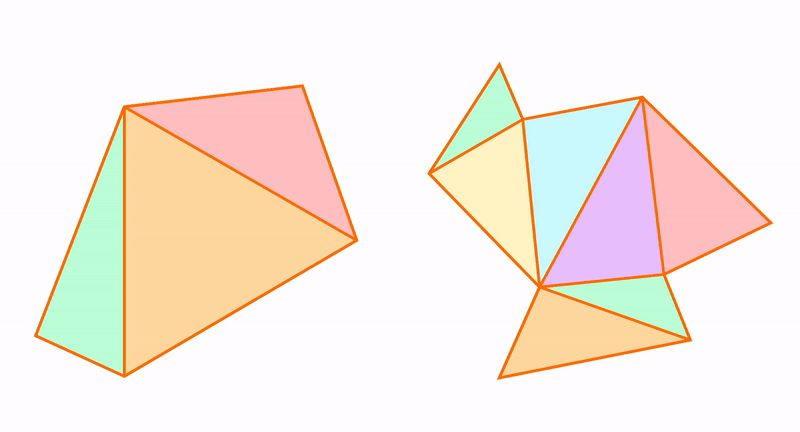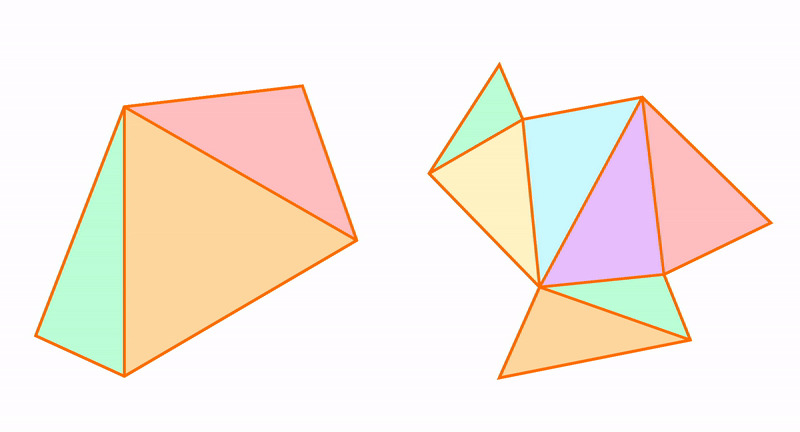
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.

Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

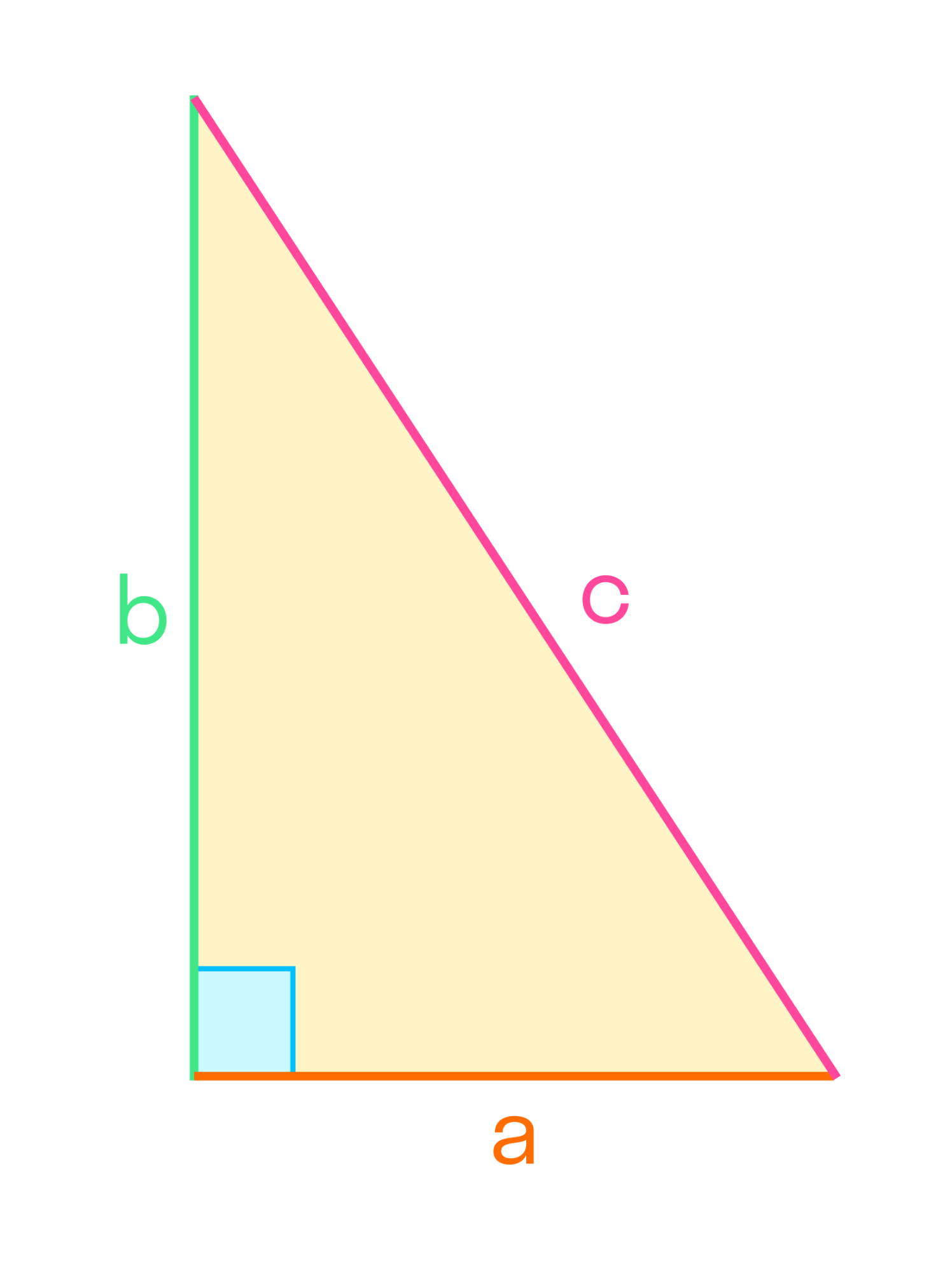
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

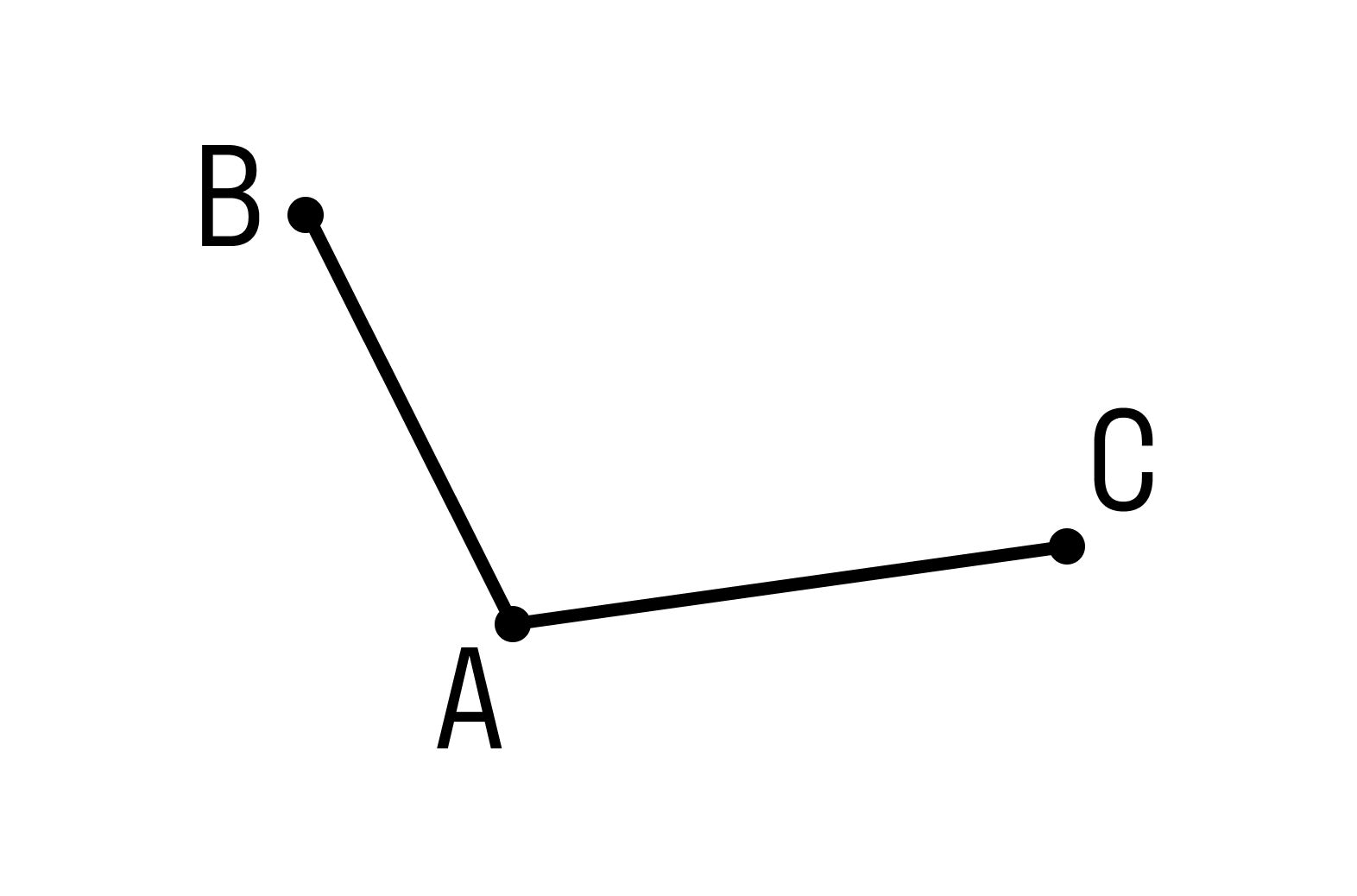
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

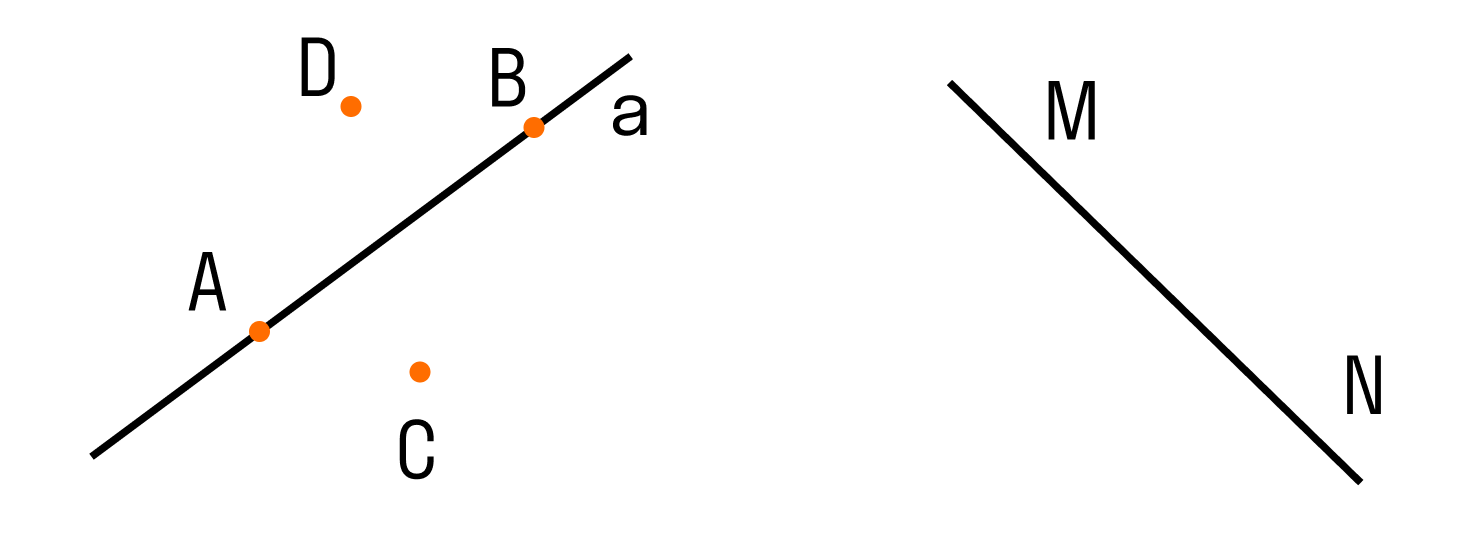
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

Два варианта расположения точек относительно прямой:

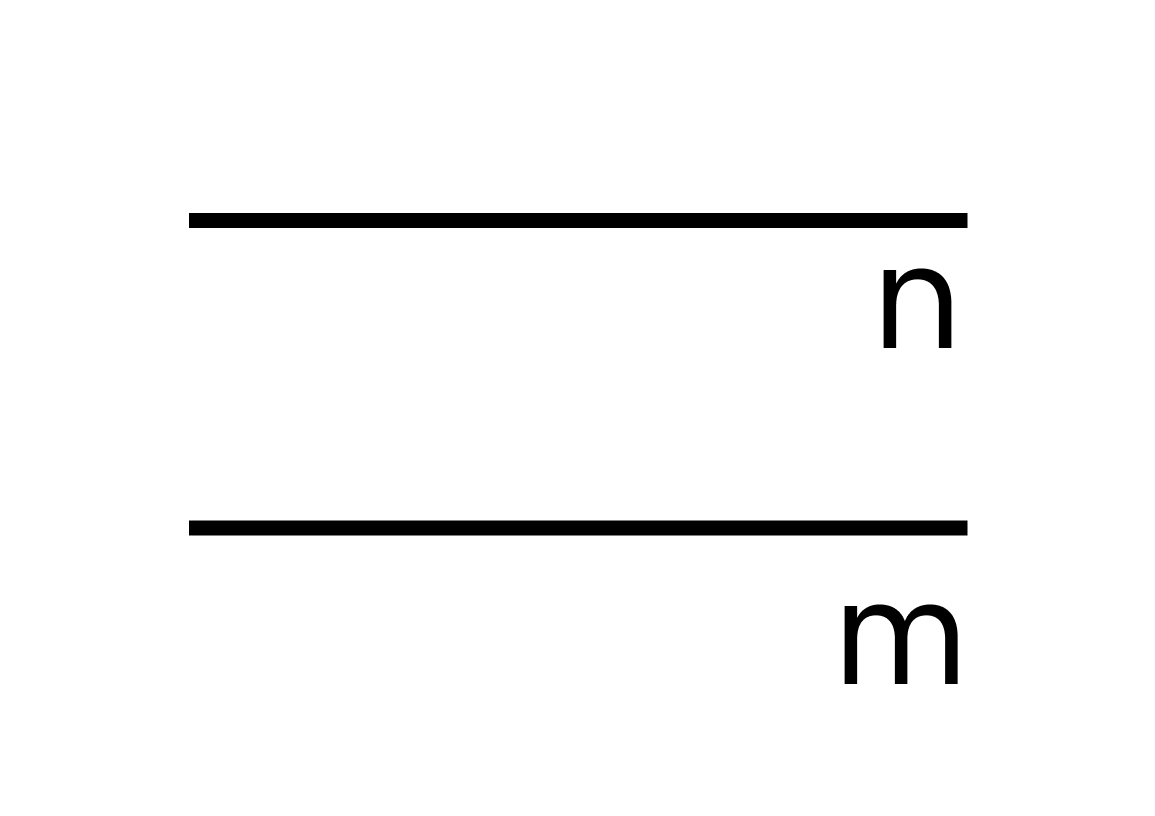
Если рассмотреть две прямые, то возможны два варианта их расположения:

Для записи не пересекающихся прямых используют специальный знак — ,
то есть m n (читают: прямая m не пересекает прямую n).

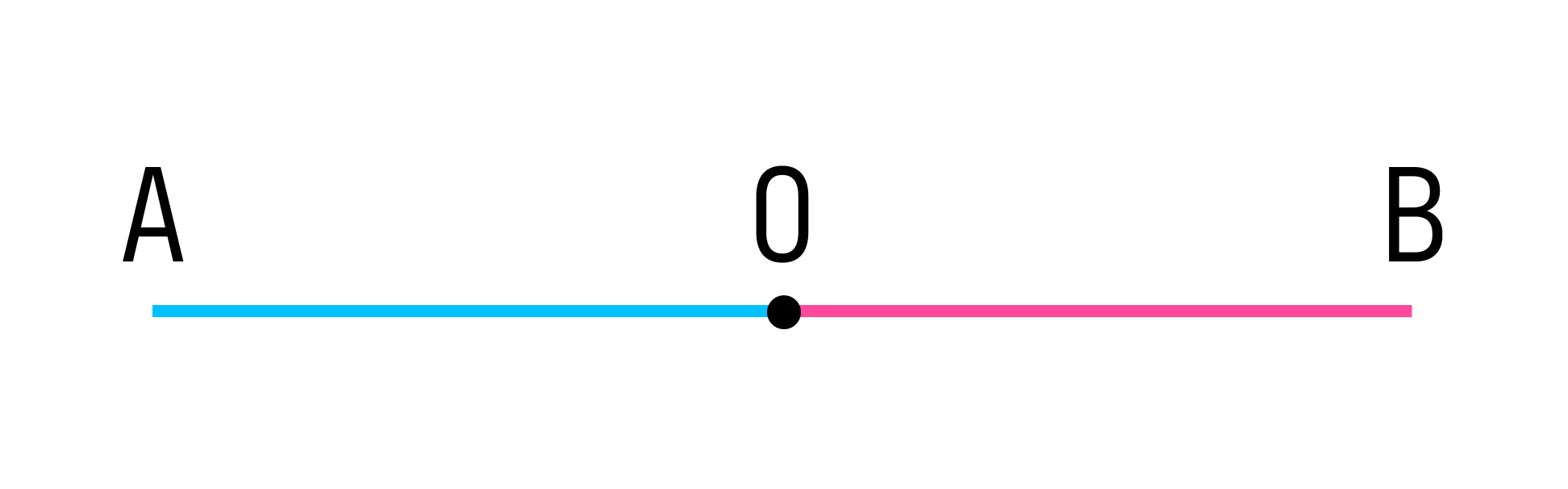
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Комбинации простейших объектов

Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).

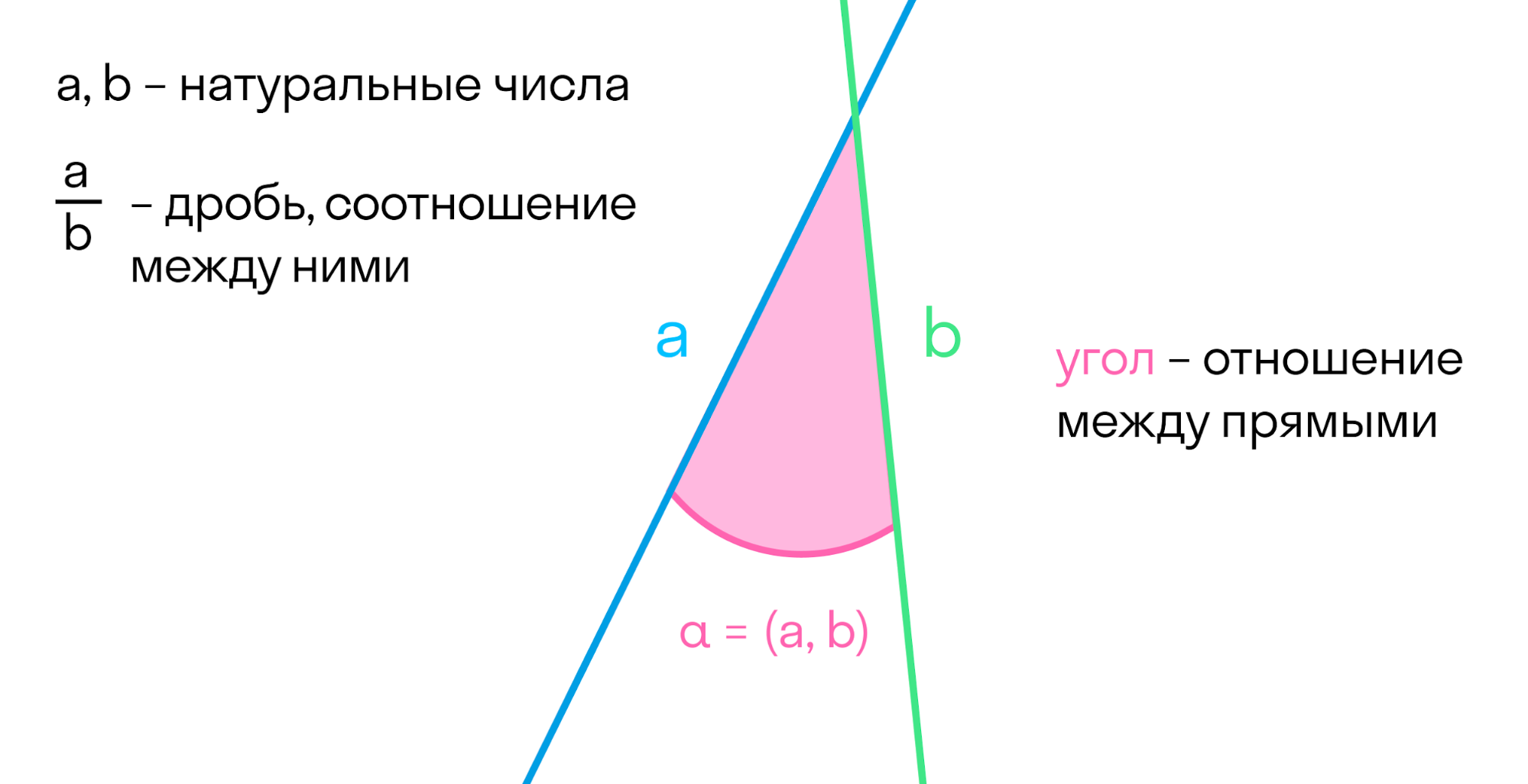
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.

Точно так же мы изучали множества, а после — отношения между множествами, функции.

Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.

Максимальный угол – это полный оборот, он составляет 360 градусов.

Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.

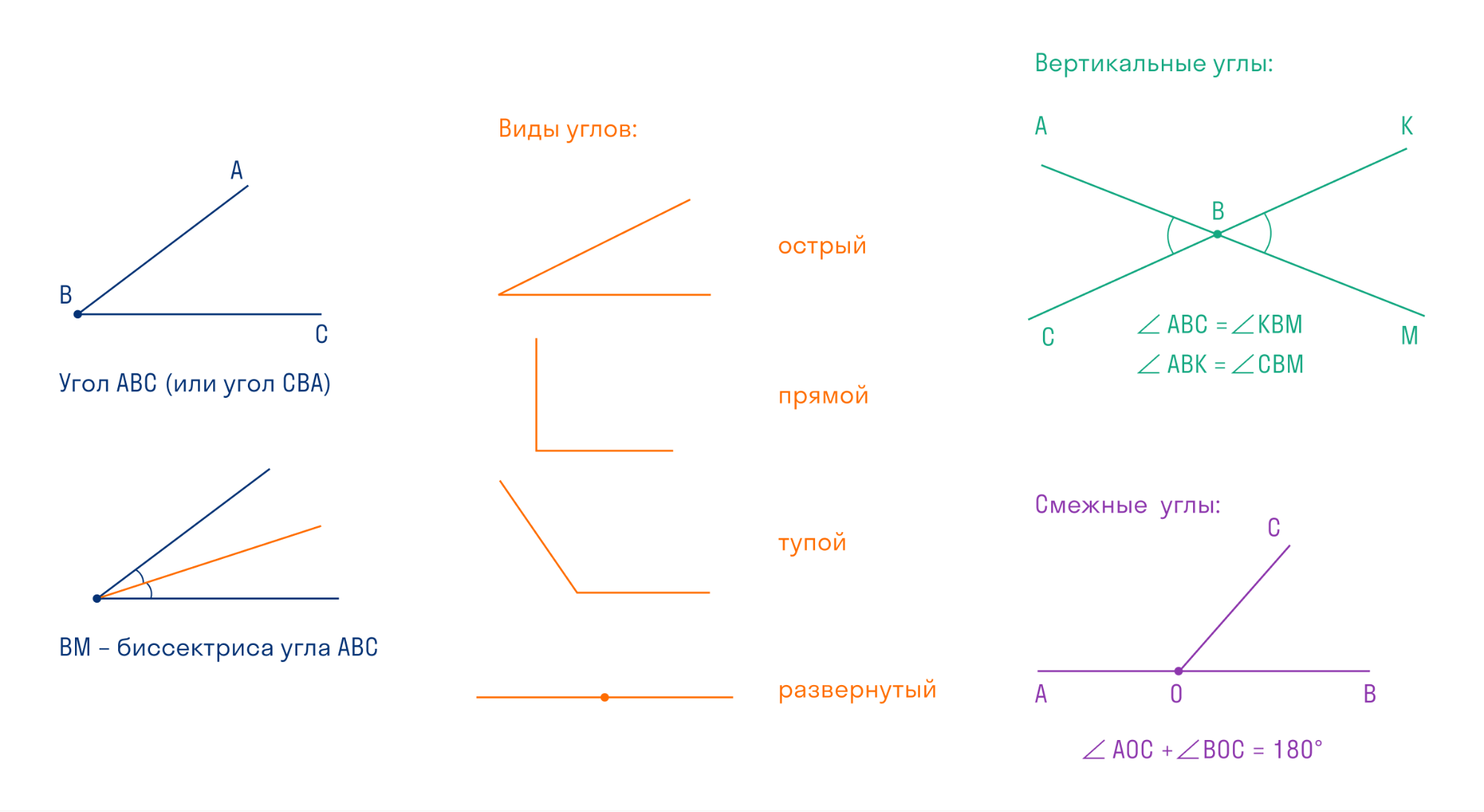
Есть разные виды углов, выделим самые часто встречающиеся:

Точка называется вершиной угла, а лучи — сторонами угла.

Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.

Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.

Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.

А теперь посмотрим на взаимное расположение трех прямых.

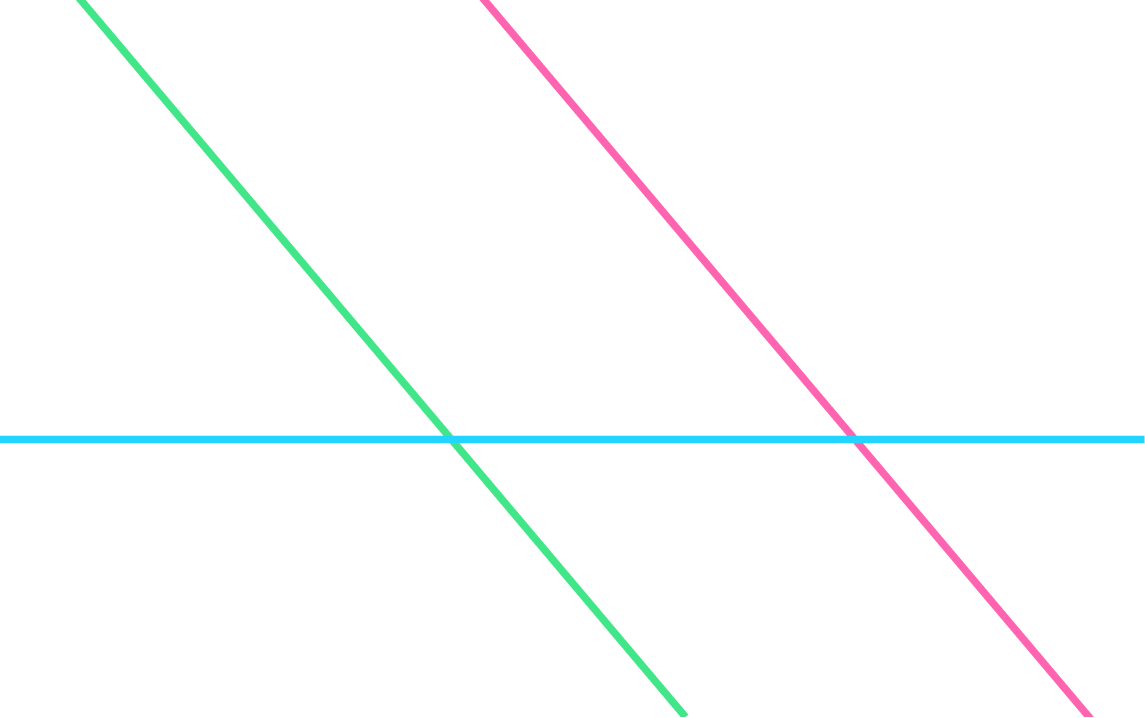
Первый случай: все три прямые параллельны.

Второй случай: две прямые параллельны, а третья их пересекает.

Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.

Треугольник

Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.

Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.

Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.

Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:

Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Сумма любых двух сторон треугольника больше его третьей стороны.

Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.

Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.

Равенство треугольников ABC и A₁B₁C₁ обозначается так: ΔABC = ΔA₁B₁C₁.

Есть даже специальные теоремы про равенство треугольников.

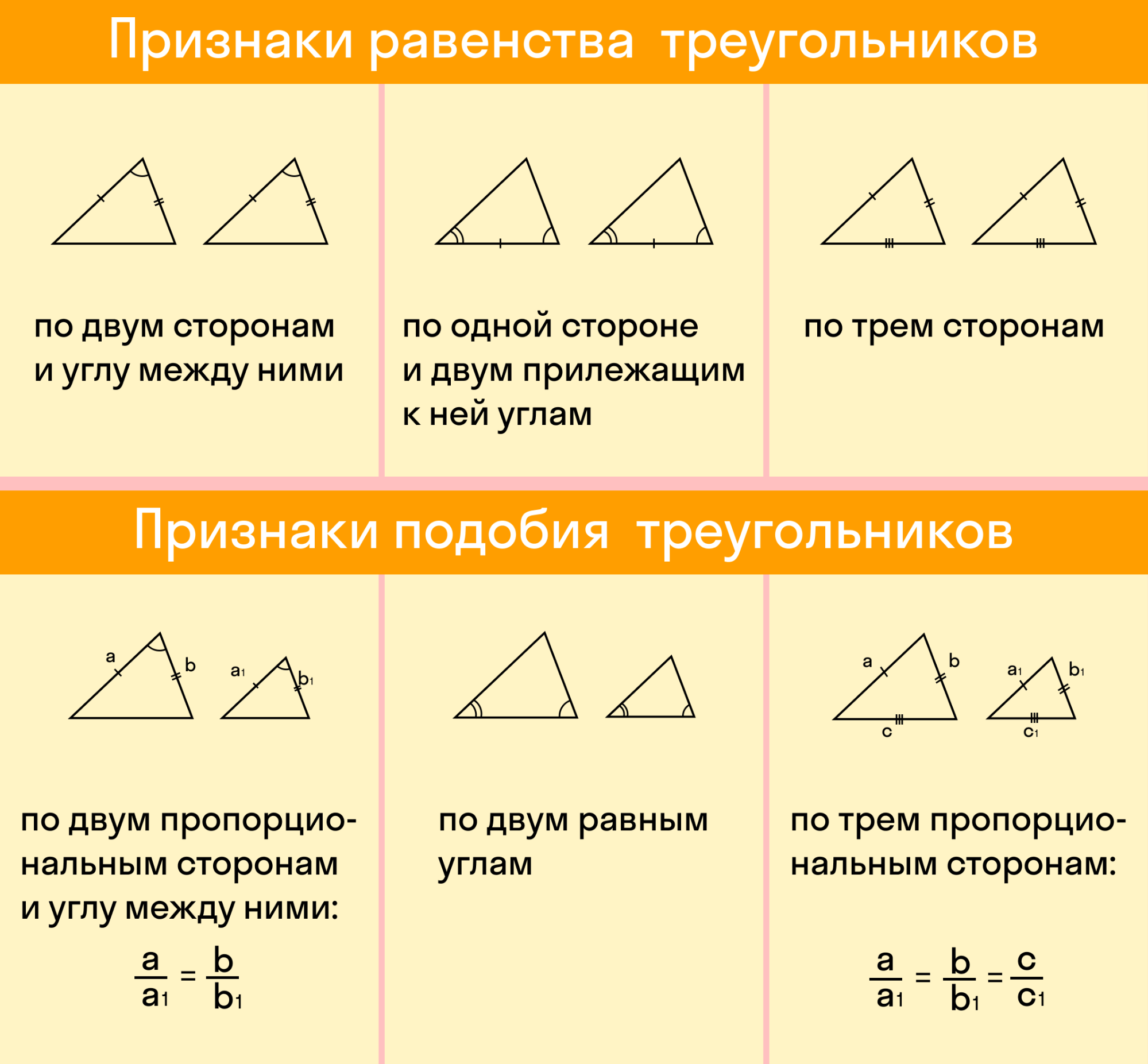
Первый признак равенства треугольников звучит так:

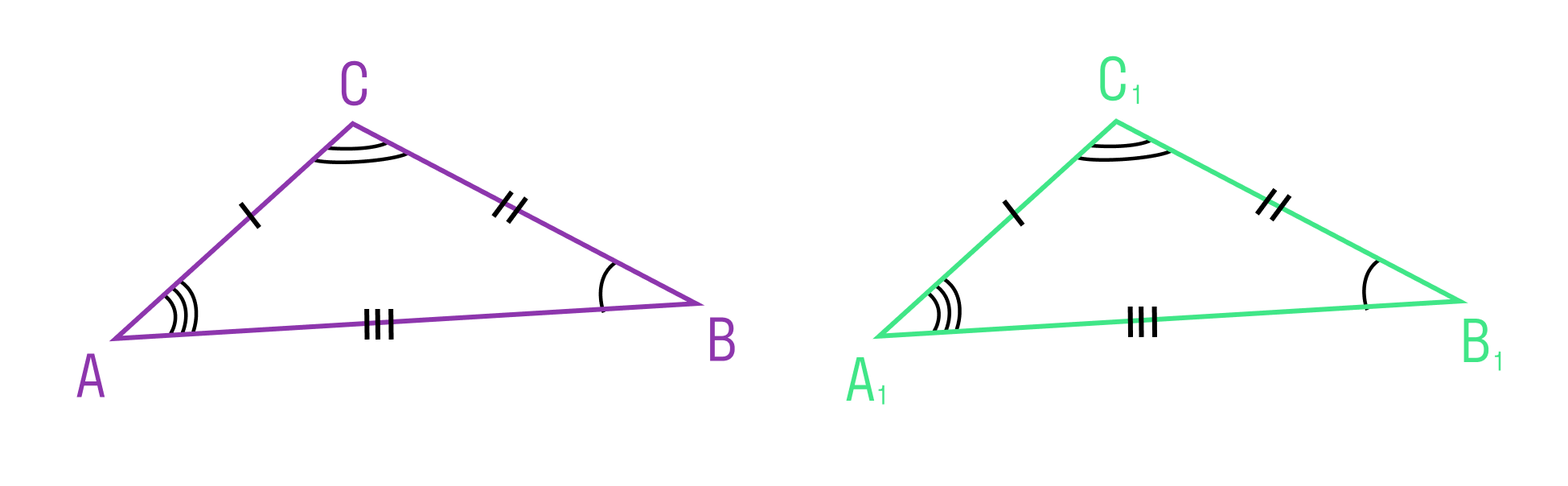
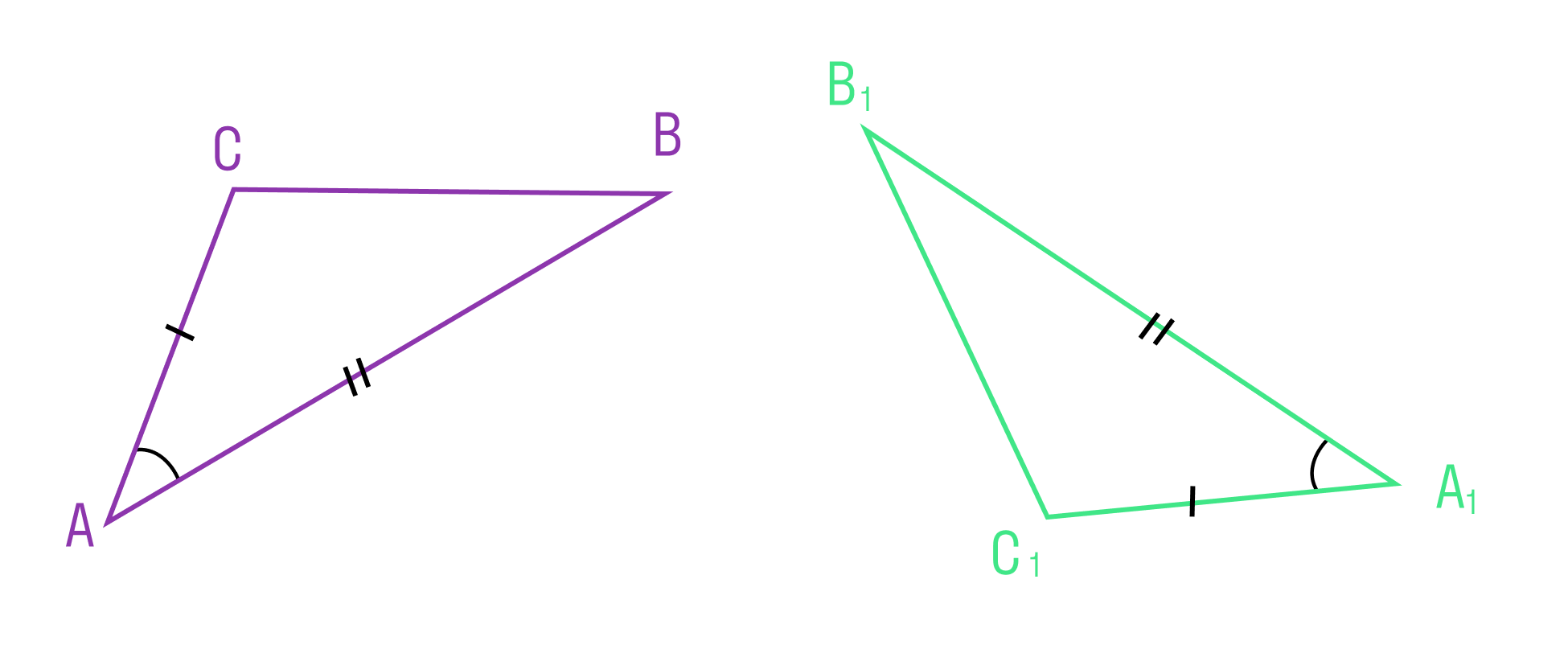
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

Второй признак равенства треугольников

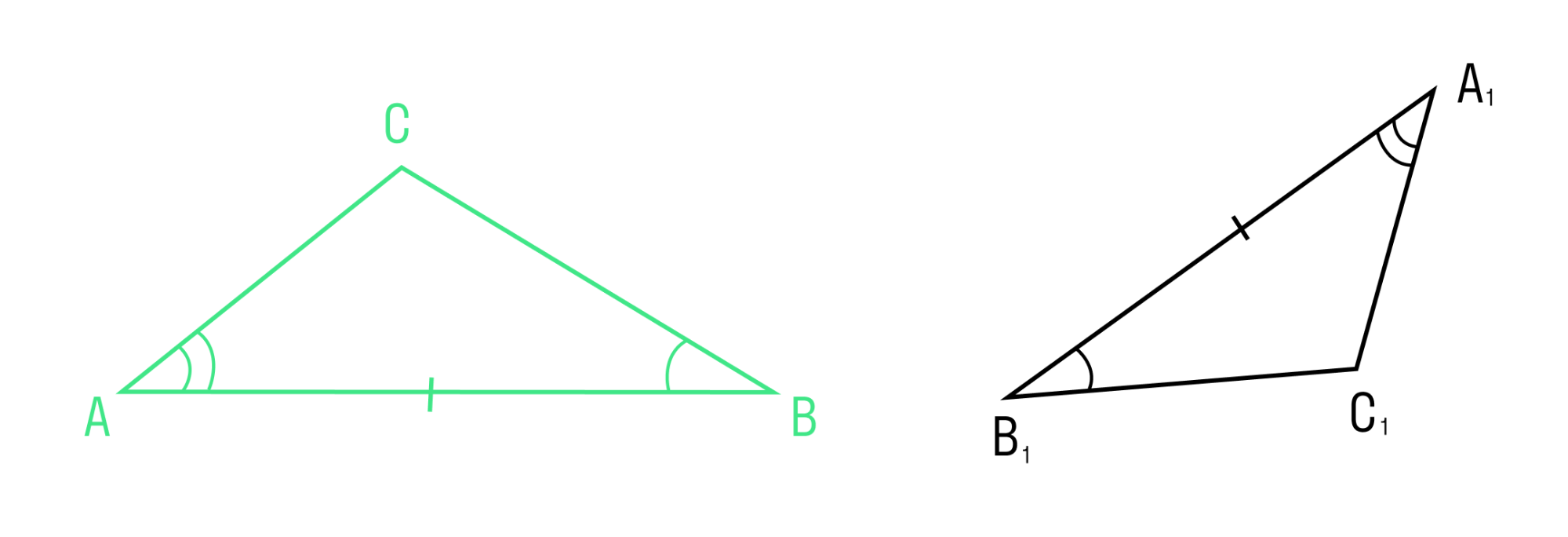
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников

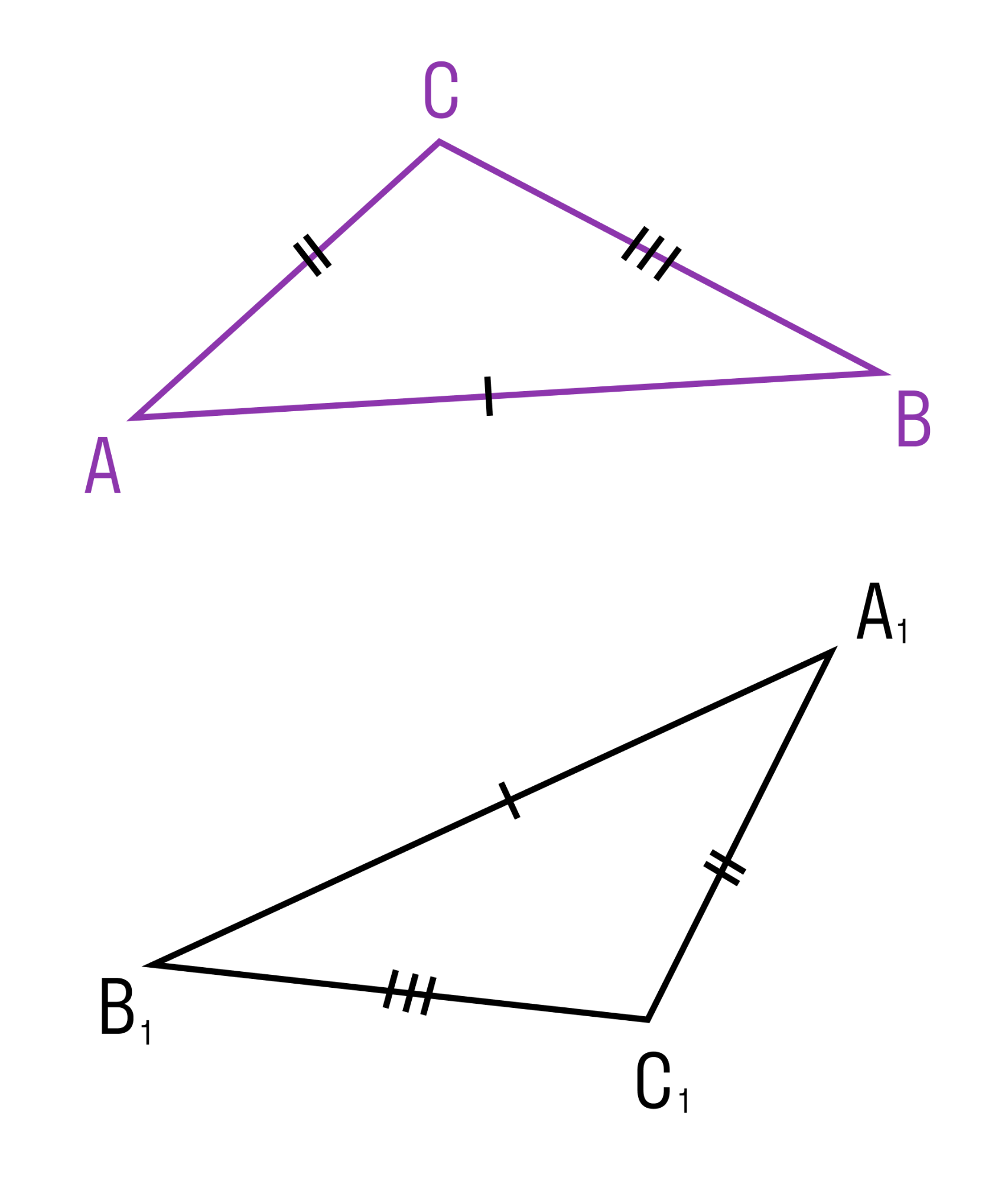
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.

Подобные треугольники

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Треугольники АВС и A₁B₁C₁ будут подобны, если

Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A₁B₁C₁ подобны, это можно записать так: ΔАВС ∾ ΔA₁B₁C₁.

Теорема о первом признаке подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

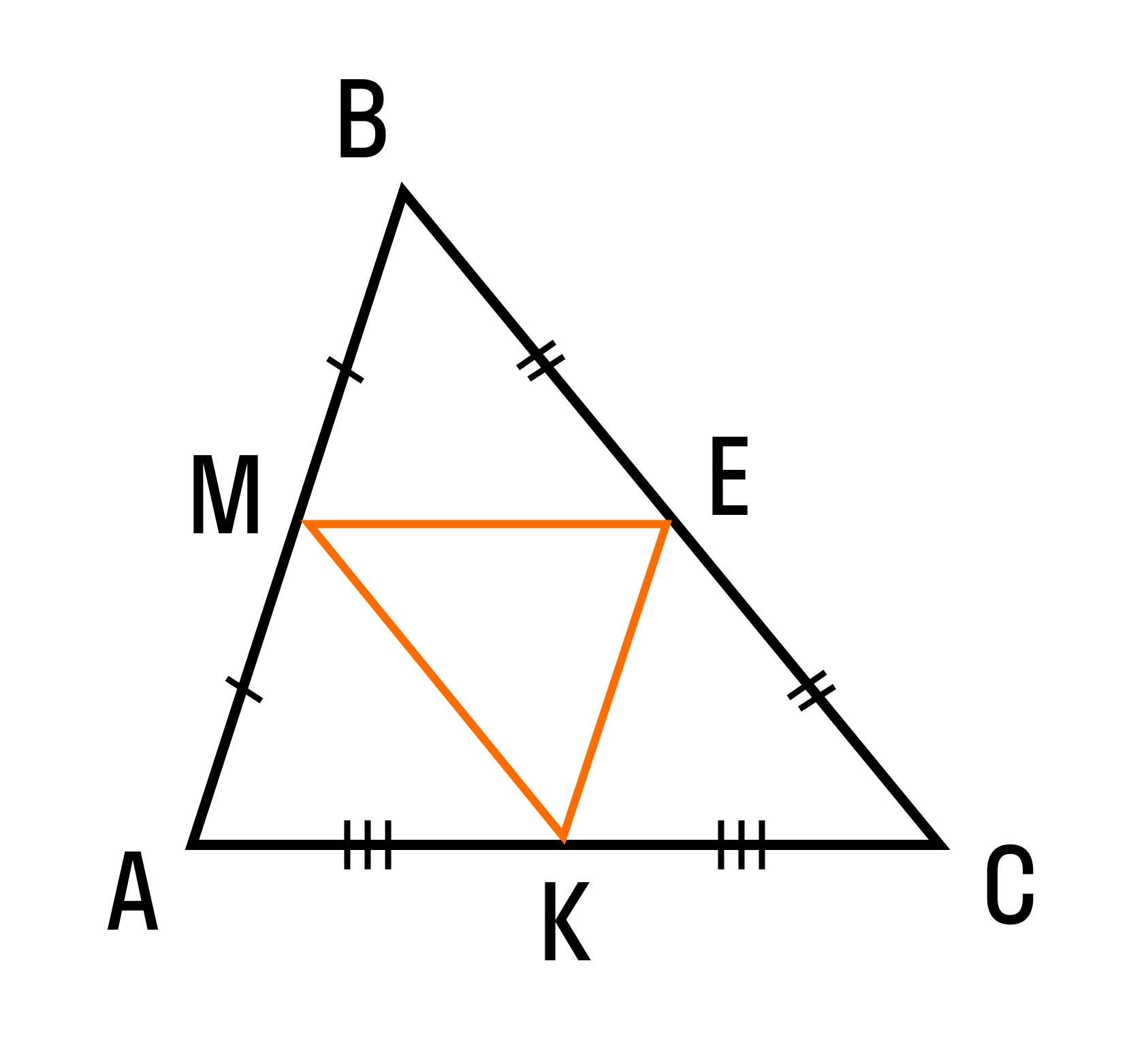
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.

На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

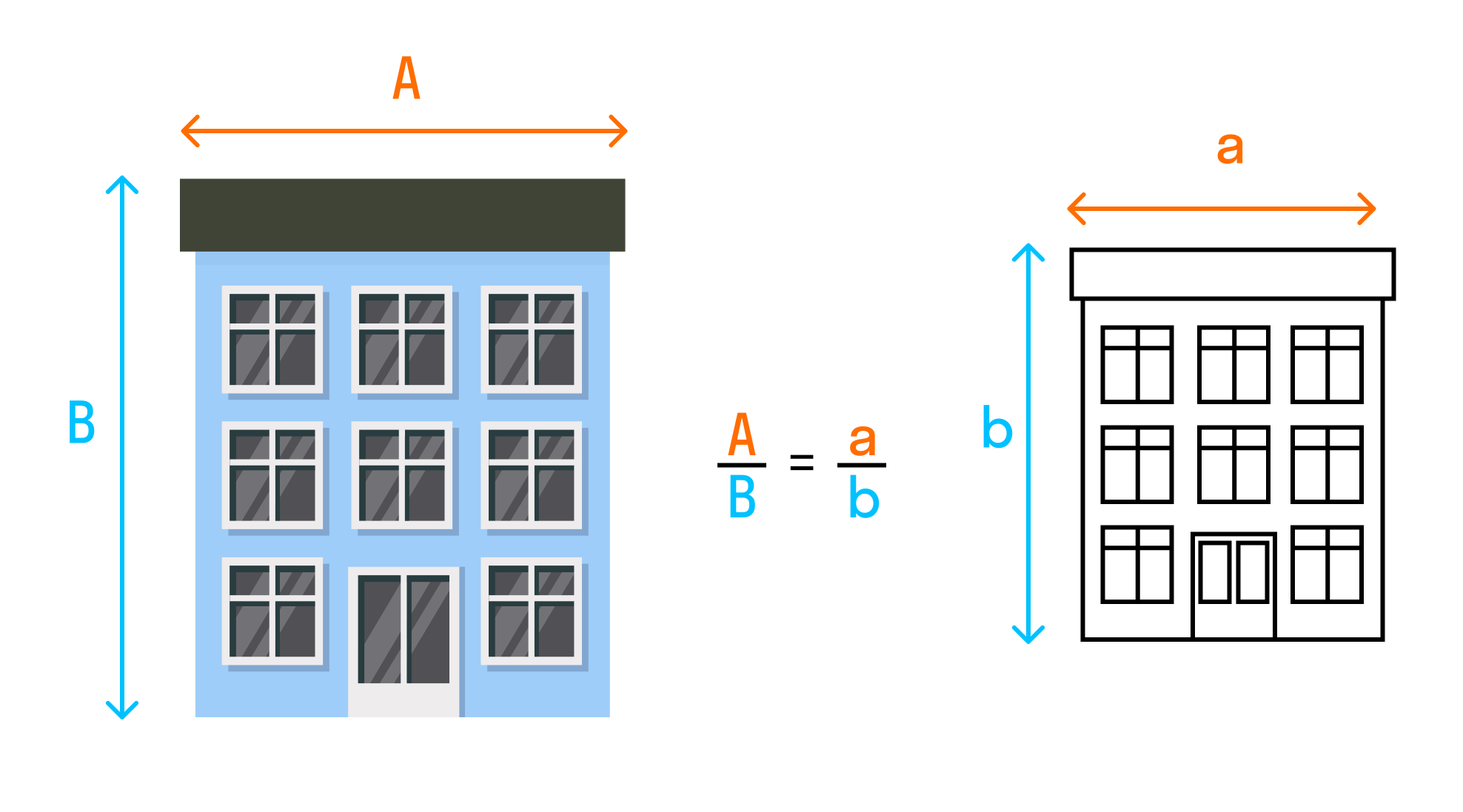
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.

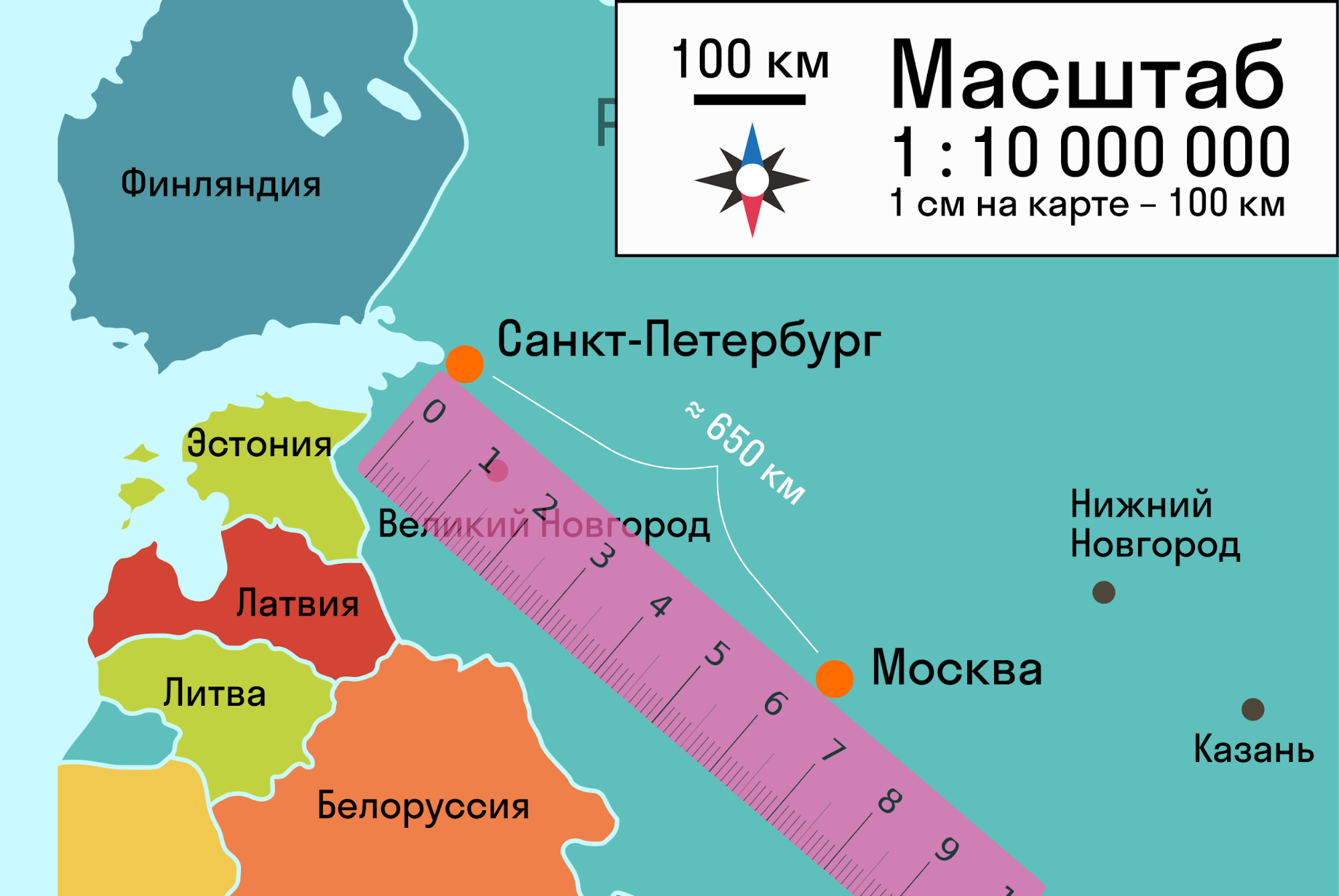
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.

Классификация треугольников по их сторонам

Для классификации треугольников можно использовать их типологию.

Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.

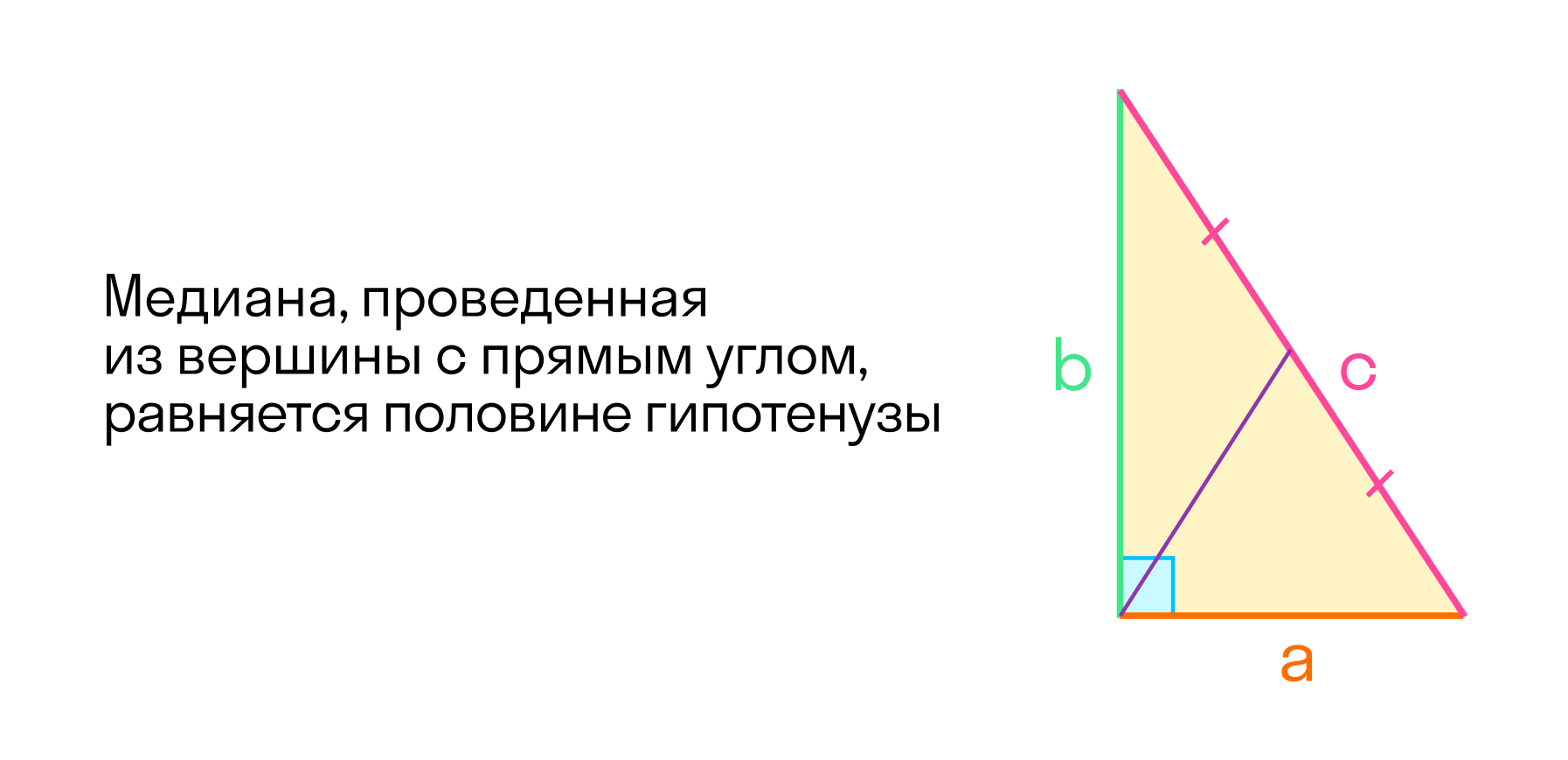
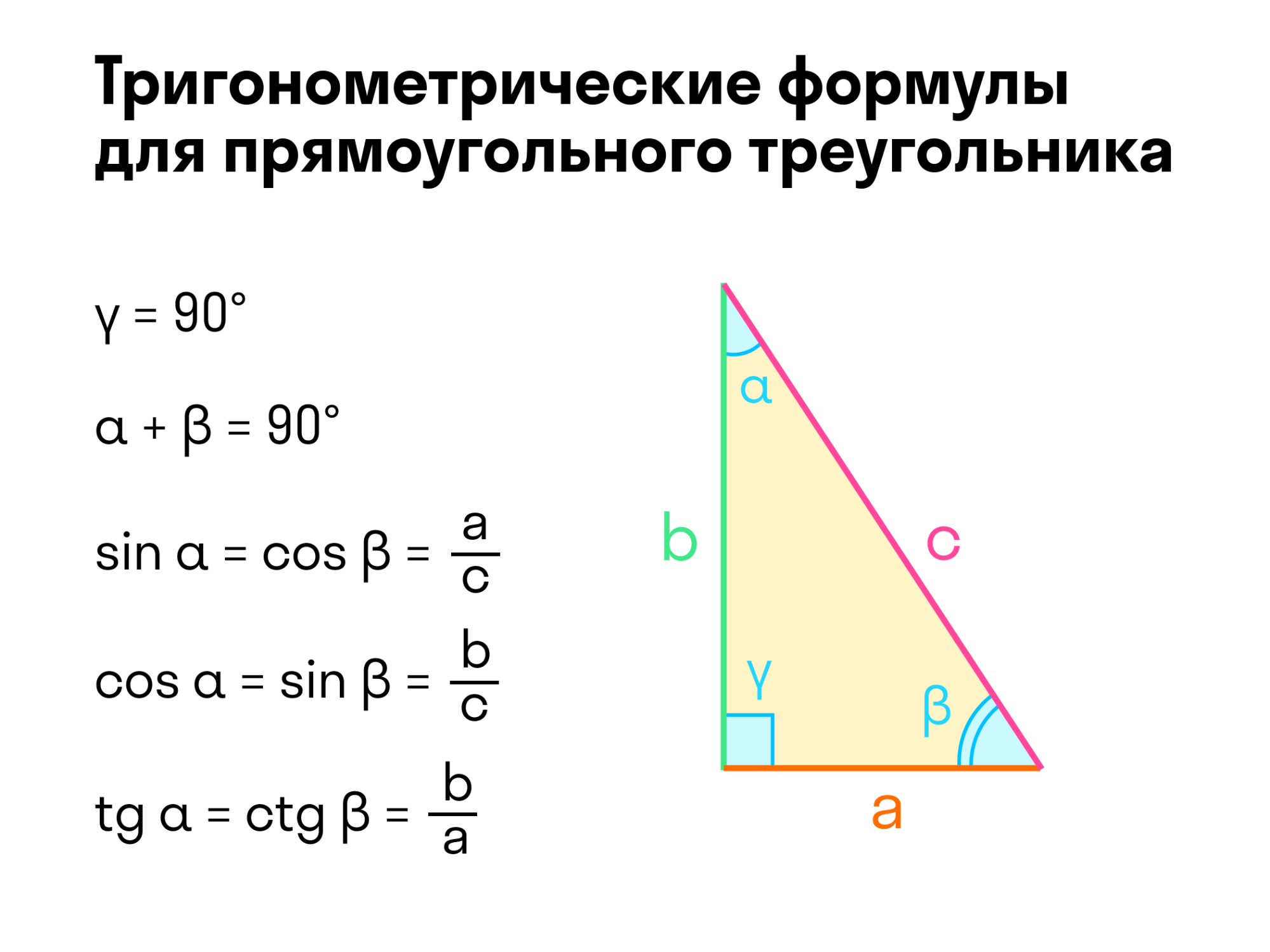
Свойства прямоугольного треугольника

С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.

Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.

Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.

Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.

От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃

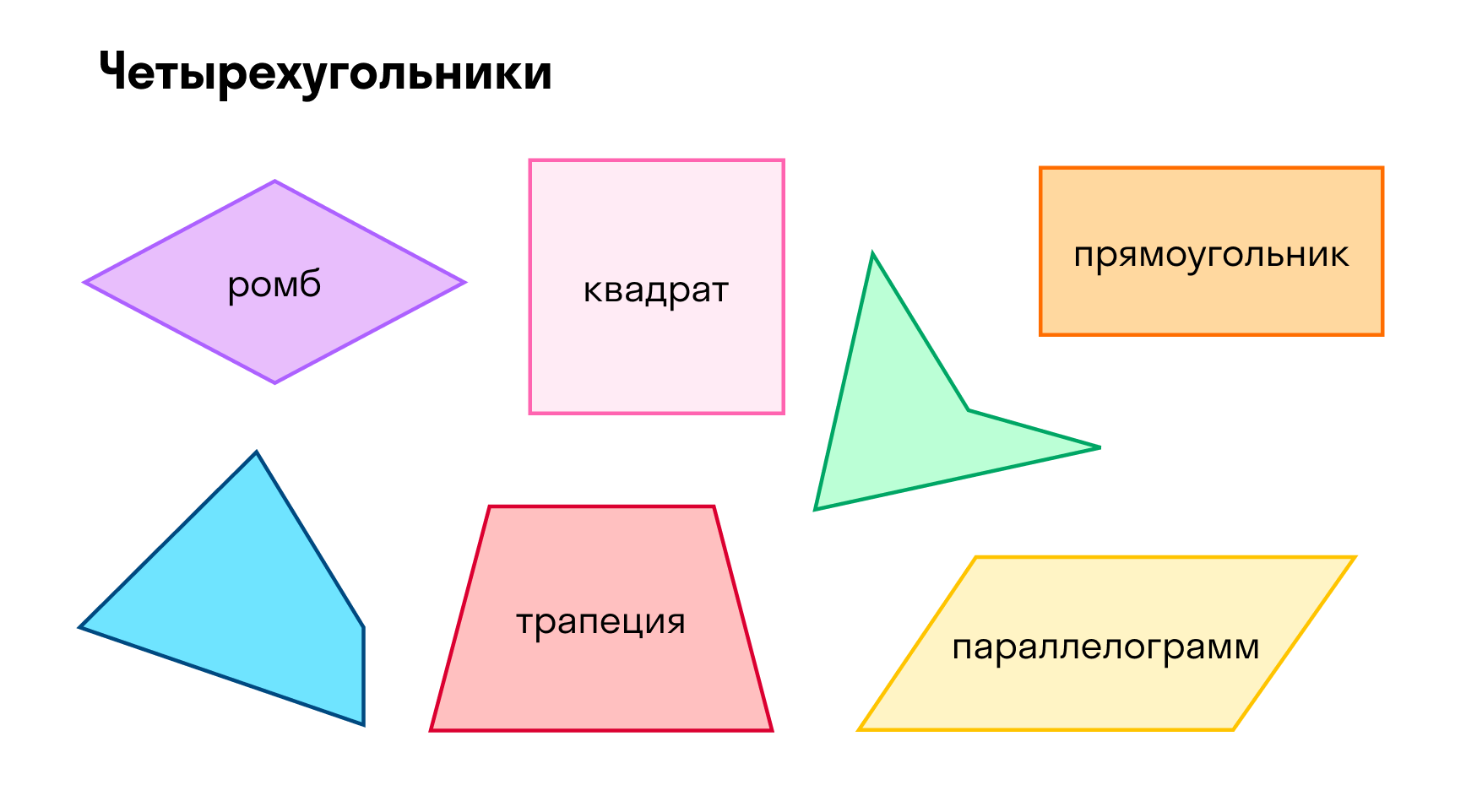
Четырехугольники

Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.

Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.

Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:

Окружность

Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.

Взаимодействие объектов

Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.

Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.

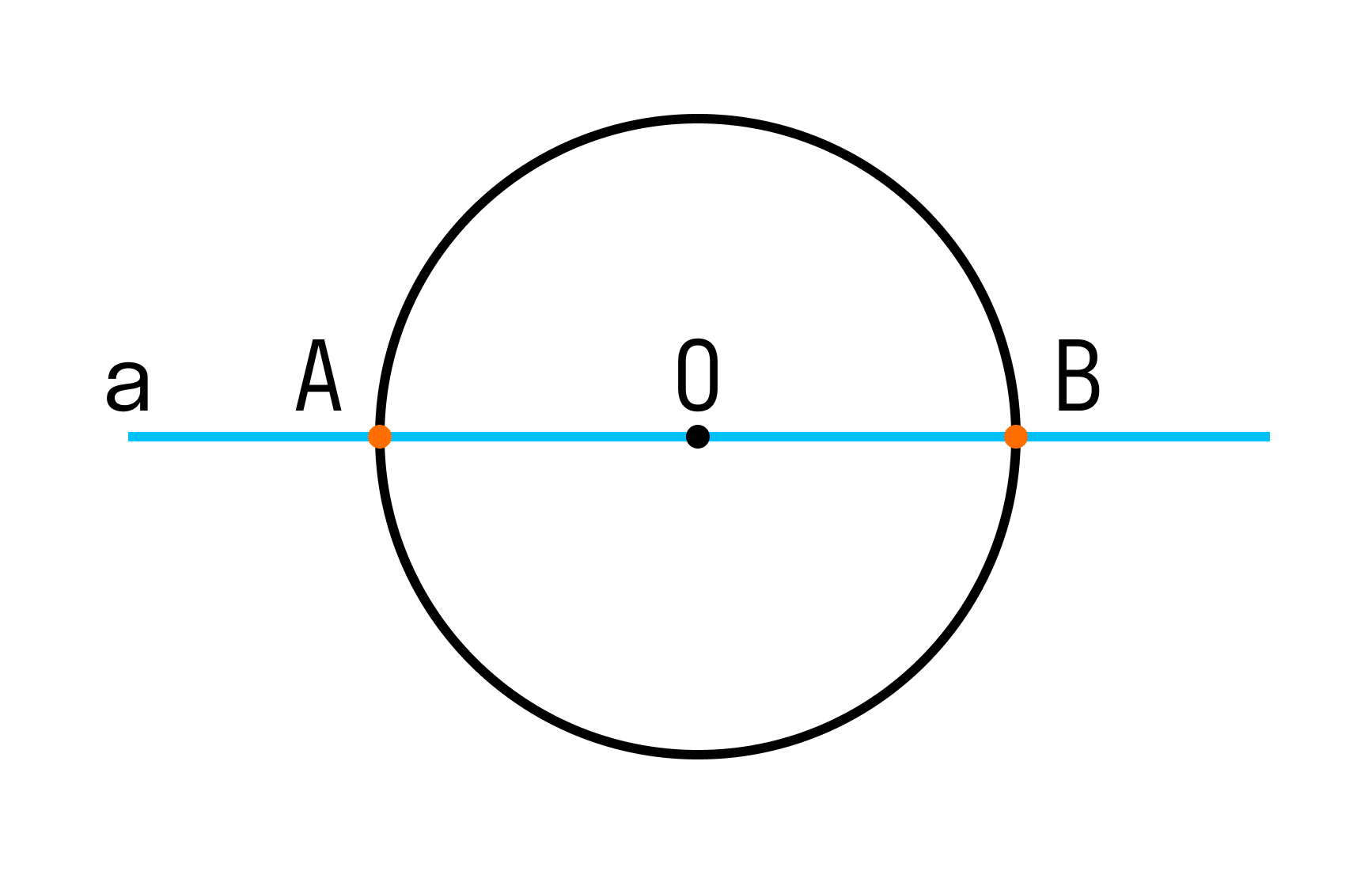
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.

На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.

Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:

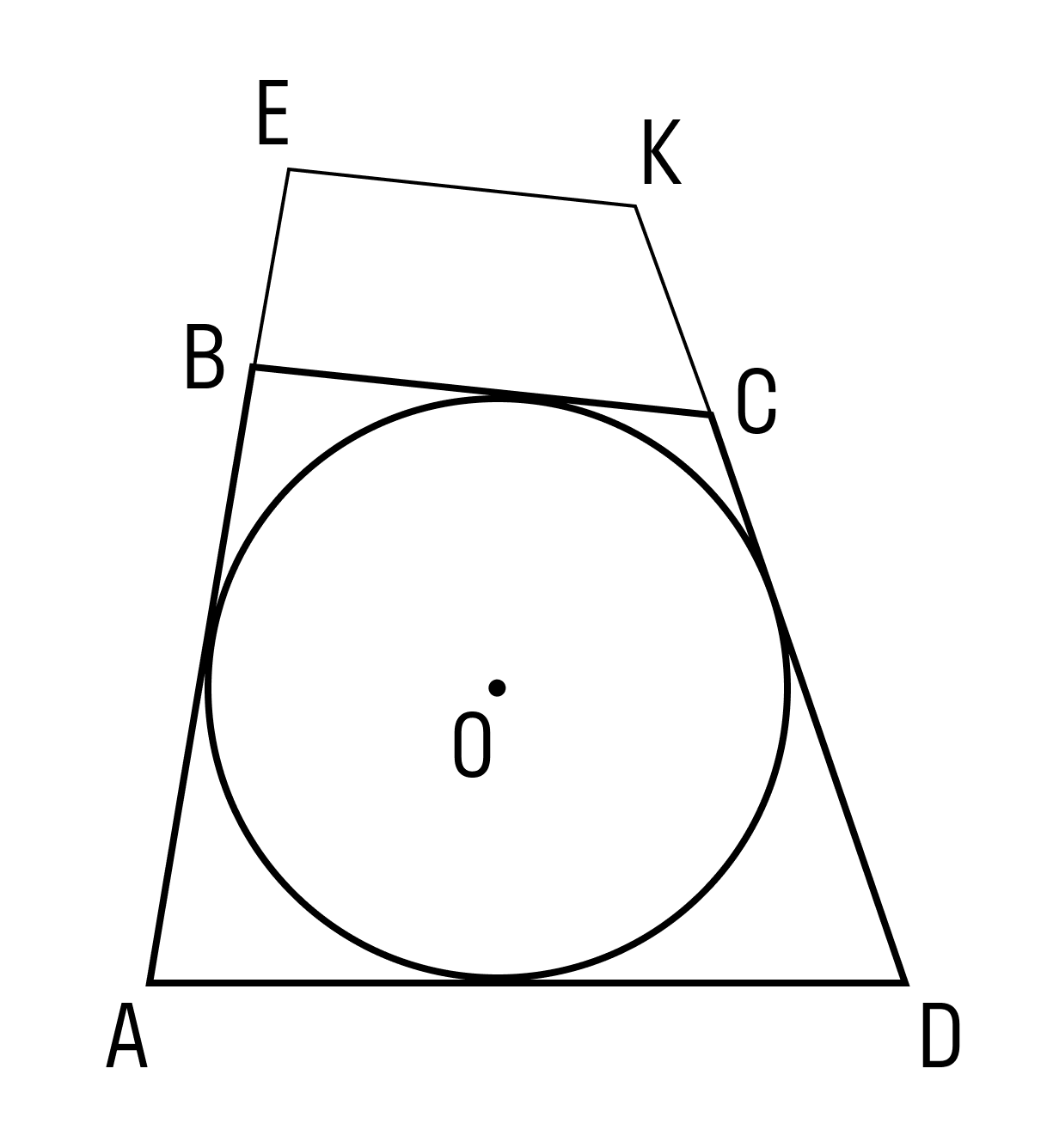
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.

На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.

Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.

Источник

ГЕОМЕТРИЯ

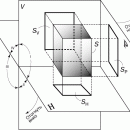
ГЕОМЕТРИЯ, раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В планиметрии рассматриваются фигуры на плоскости; в стереометрии изучаются пространственные фигуры.

ИСТОРИЯ

Египет.

Если не учитывать весьма скромный вклад древних обитателей долины между Тигром и Евфратом и Малой Азии, то геометрия зародилась в Древнем Египте до 1700 до н.э. Во время сезона тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложения нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянами стали такие виды их деятельности, как возведение пирамид и изобразительное искусство.

Основным источником наших знаний о древнеегипетской геометрии является относящийся примерно к 1700 до н.э. папирус Ринда, названный по имени владельца, египтолога Ринда (этот папирус также называется папирусом Ахмеса) и хранящийся ныне в Лондоне в Британском музее. Папирус Ринда свидетельствует о том, что древних египтян интересовали главным образом практические аспекты геометрии и что при накоплении геометрических фактов египтяне почти всецело руководствовались интуицией, экспериментом и приближенными представлениями.

Греция.

Около 600 до н.э. ионийские греки, совершившие путешествие в Египет, привезли на родину первые сведения о геометрии. Самым известным путешественником в Египет был Фалес (ок. 640 – ок. 546 до н.э.). Он был преуспевающим купцом, посвятившим последние годы жизни науке и политике. Фалес первым начал доказывать истинность геометрических соотношений, последовательно выводя их логически из некоторого набора общепринятых утверждений, называемых аксиомами или постулатами. Этот метод дедуктивного рассуждения, которому предстояло стать доминирующим в геометрии и фактически – во всей математике, сохраняет свое фундаментальное значение и в наши дни.

Одним из наиболее знаменитых учеников Фалеса был Пифагор (ок. 570 – ок. 500 до н.э.). Он много путешествовал, а потом поселился в Кротоне, в Италии, где основал общество, занимавшееся изучением арифметики, музыки, геометрии и астрономии. Пифагор и его последователи доказали много новых теорем о треугольниках, окружностях, пропорциях и некоторых трехмерных телах. Пифагор доказал также знаменитую теорему, носящую ныне его имя, согласно которой площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

Пифагор умер в изгнании, но его влияние на греческих математиков ощущалось на протяжении многих веков. После его кончины в Элее (город в Италии) новыми центрами развивающейся геометрии становились по очереди Афины и Александрия. Архит Тарентский (ок. 428 – ок. 365 до н.э.) и Гиппий Элидский (р. ок. 425 до н.э.) затратили много усилий на решение трех задач, игравших важную роль в древнегреческой математике: это задачи о трисекции угла, о построении квадрата, площадь которого равна площади данного круга (задача о квадратуре круга), и о построении куба, имеющего вдвое больший объем, чем данный куб (задача об удвоении куба). Хотя ныне известно, что с помощью циркуля и линейки (единственных орудий геометрических построений, известных древнегреческим математикам) эти задачи решить нельзя, тем не менее попытки это сделать не были напрасны. Они стимулировали изучение конических сечений и способствовали совершенствованию математических методов.

Александрия.

Афинская школа числила в своих рядах таких великих людей, как Платон и Аристотель. После смерти Аристотеля центр научной мысли переместился в Александрию (Египет), где в начале 3 в. до н.э. был основан знаменитый Александрийский Мусейон – один из главных научных центров античного мира. Живший в Александрии математик Евклид (3 в. до н.э.), биографические сведения о котором крайне скудны, собрал в 13 книгах своего сочинения значительную часть математических знаний того времени. Семь книг из 13 были посвящены геометрии, предмет которой был им тщательно и систематически изложен, различные утверждения и теоремы расположены в определенном порядке и перенумерованы. Была включена также теория пространственных тел, ограниченных плоскими поверхностями. Называлось это великое сочинение Начала, и последующие издания, точно придерживающиеся оригинала, стали основой обучения геометрии вплоть до нашего времени. Величайшим математиком античности был грек Архимед (ок. 287–212 до н.э.). Кроме множества других полученных им научных результатов и открытий, Архимед расширил ту часть Начал Евклида, в которой рассматривались пространственные тела, включив в их число сферу, цилиндр и конус. Другими великими александрийскими геометрами были Аполлоний Пергский (3 в. до н.э.; конические сечения), Птолемей (2 в. н.э.; астрономия) и Папп (3 в. н.э.; плоские кривые высших порядков). В 641 н.э. арабы разграбили Александрию и разрушили Мусейон и его библиотеку. Впрочем, греческая математика вступила в период застоя еще в начале 4 в. н.э, после кончины Паппа. См. также ДРЕВНЯЯ ГРЕЦИЯ.

Средневековье.

После падения Александрии большинство работ древнегреческих математиков были рассеяны или утрачены. Некоторые из них, в том числе Начала Евклида, были переведены и изучались арабами и индийцами. И хотя эти народы породили нескольких великих математиков, среди которых наиболее известны индийские математики Ариабхата (ок. 476 – ок. 550) и Бхаскара II (ок. 1114–1185), все же их самой большой заслугой следует считать сохранение геометрии в период Средневековья.

После падения Римской империи в 5 в. наука в Европе долгое время находилась почти в полном забвении. В 12 и 13 вв. Начала были переведены с греческого и арабского на латынь и современные европейские языки, а геометрия вошла в программу монастырских школ. Первый из этих переводов был выполнен Аделардом Батским в 1120.

Новое время.

За последние 300 лет доказательная геометрия была существенно расширена, а по своим методам и степени общности результатов она стала заметно отличаться от элементарной геометрии (т.е. геометрии, изложенной в Началах). Французский математик Ж.Дезарг (1593–1662) в связи с развитием учения о перспективе занялся исследованием свойств геометрических фигур в зависимости от их проекций. Тем самым он заложил основу проективной геометрии, которая изучает те свойства фигур, которые остаются неизменными при различных проекциях. В 19 в. это направление получило существенное развитие. Проективная геометрия, конические сечения и новая геометрия треугольников и окружностей составили содержание современной т.н. чистой геометрии.

Тесно связанная с проективной, начертательная геометрия была введена французским математиком Г.Монжем (1746–1818). Эта новая область геометрии была связана с представлением изображений геометрических фигур на плоскости и определением геометрическими средствами расстояний, углов и линий пересечения. Начертательная геометрия представляет собой основу технического черчения.

В 1637 Р.Декарт (1596–1650), французский философ и математик, опубликовал свою Геометрию – первый труд по аналитической геометрии, позволивший применить в геометрии мощные алгебраические методы. Геометрические задачи всех видов теперь могли решаться в рамках единого подхода; кроме того, благодаря новым методам стала возможной постановка и решение новых задач, о которых древние не могли даже помыслить, но которые ныне находятся в самом центре математики и математической физики.

Со времен первого появления Начал математики тщетно пытались доказать пятый постулат Евклида: через точку, не лежащую на прямой, можно провести только одну прямую, ей параллельную. В 19 в. было доказано, что можно построить непротиворечивую геометрию, используя все аксиомы и постулаты Евклида и отрицание постулата о параллельных, а это означало, что искомого доказательства пятого постулата не существует. Любая такая непротиворечивая геометрия получила название неевклидовой геометрии. Около 1830 Я.Бойяи (1802–1860) и Н.И.Лобачевский (1792–1856) независимо друг от друга построили геометрию, использовавшую постулат, согласно которому через точку, лежащую вне прямой, можно провести много прямых, ей параллельных. В 1854 Б.Риман (1826–1866) сформулировал постулат, согласно которому через точку вне прямой невозможно провести ни одной параллельной, что дало начало т.н. римановой геометрии. Неевклидова математика расширилась и стала включать в себя тригонометрию, аналитическую и дифференциальную геометрии, охватив не только планиметрию, но и стереометрию, а также геометрию пространств размерности больше трех (геометрию гиперпространств). Евклидова и обе неевклидовы геометрии одинаково хорошо служат для описания той ограниченной области пространства, в которой мы живем, хотя геометрия Евклида проще по форме. В то же время при переходе к римановой геометрии некоторые современные физические теории существенно упрощаются. См. также МАТЕМАТИКИ ИСТОРИЯ.

ЭЛЕМЕНТАРНАЯ ПЛАНИМЕТРИЯ

Аксиомы и постулаты.

Существует набор исходных посылок, называемых аксиомами и постулатами, на которых базируется вся структура геометрии.

Аксиомы.

Аксиомы – это утверждения, принимаемые за истинные без доказательств. Аксиомы обычно подразделяются на две группы: общие, относящиеся ко всей математике, и геометрические.

К числу общих аксиом относятся следующие.

1. Равные одному и тому же равны между собой.
2. Если к равным прибавляются равные, то суммы будут равны.
3. Если от равных отнимаются равные, то остатки будут равны.
4. Если равные умножить на равные, то произведения будут равны.
5. Если равные разделить на равные, то частные будут равны. Деление на нуль запрещается.
6. Одинаковые степени равных, а также корни одинаковой степени из равных равны.
7. Целое больше любой своей части.
8. Целое равно сумме своих частей.

К числу геометрических аксиом относятся следующие.

1. Через любые две данные точки можно провести только одну прямую.
2. Геометрическую фигуру можно перемещать в пространстве, не изменяя ни ее размеров, ни ее формы.
3. Геометрические фигуры, которые совпадают после наложения, конгруэнтны (т.е. равны).
4. Прямая есть кратчайшее расстояние между двумя точками.

Постулаты.

Следующие постулаты касаются построений и принимаются за истинные без доказательств.

1. Через любые две данные точки можно провести прямую.
2. Прямая может быть продолжена бесконечно или же ограничена в любой своей точке.
3. Окружность может быть описана вокруг любой данной точки как центра и с любым радиусом.
4. Все прямые углы равны.
5. Через точку, не лежащую на прямой, можно провести одну и только одну прямую, ей параллельную.

Некоторые геометрические фигуры, построения и заключения.

Многие термины, используемые для описания фигур в геометрии, настолько фундаментальны, что определить их не представляется возможным. Все попытки сделать это приводили лишь к замене одних терминов другими, столь же неопределимыми, или к простому описанию некоторых свойств фигур. Например, термин «точка» не поддается определению.

Линии.

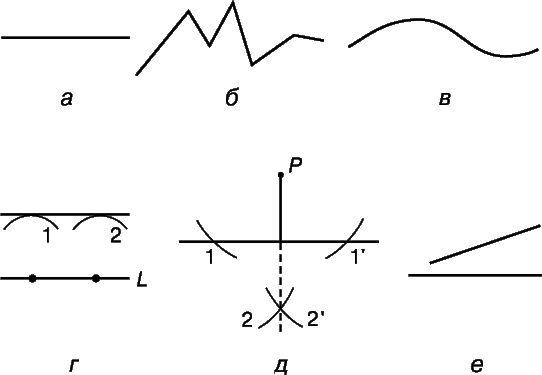
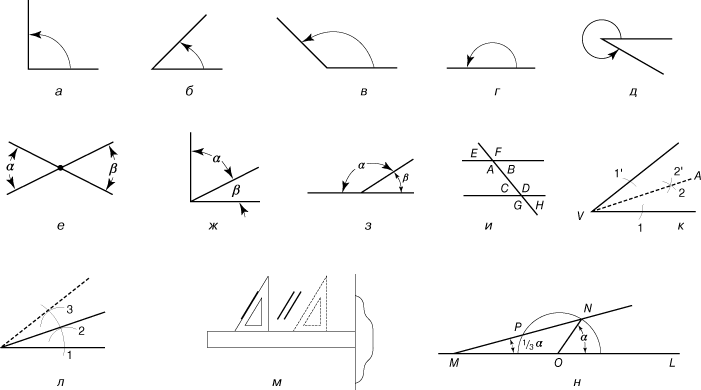
Термин «линия» (или «кривая» в широком смысле слова) не имеет определения, хотя мысленно линию можно представить как след движущейся точки. Бесчисленные попытки определить прямую линию (рис. 1,а) не имели успеха. Многие из этих попыток апеллировали к физическому эксперименту, например, «прямая – это туго натянутая линия». Чаще других приводится описание прямой, предложенное Архимедом: «Прямая – это кратчайшее расстояние между двумя точками». Это «определение», однако, лишь заменяет неопределяемое понятие прямизны столь же неопределяемым понятием расстояния. Предполагается, что прямая бесконечна, т.е. ее можно неограниченно продолжить в обе стороны. Часть прямой называется отрезком. Ломаная (рис. 1,б) состоит из прямолинейных отрезков. Кривой (рис. 1,в) называется линия, никакая часть которой не является прямой.

Как показано на рис. 1,г, 1,д и 1,е, прямые могут быть параллельными, перпендикулярными и наклонными. Параллельные прямые – это прямые, расстояние между которыми всюду одинаково. На рис. 1,г показано, как построить прямую, параллельную данной прямой L и отстоящую от нее на заданное расстояние. Берется окружность, радиус которой равен данному расстоянию. Проводятся две дуги с центрами в двух различных точках прямой L. Прямая, касательная к обеим дугам, и есть та прямая, которую требовалось построить.

На рис. 1,д показано, как построить прямую, проходящую через точку Р и перпендикулярную прямой L. Порядок, в котором делаются засечки дугами, указаны номерами [первыми следует провести (в любой последовательности) либо дугу 1, либо дугу 1ў]. Для проведения дуг 2 и 2ў циркуль устанавливается в точки пересечения прямой L дугами 1 и 1ў соответственно, радиусы остаются те же самые. Прямая, проходящая через точку Р и точку пересечения дуг 2 и 2ў, есть искомый перпендикуляр. Перпендикуляр – это кратчайшая линия, которую можно провести от точки до прямой, на которую он опущен, и расстояние от точки до прямой по определению равно длине перпендикуляра, опущенного из нее на прямую.

Углом называется фигура, образованная двумя полупрямыми, исходящими из одной точки. Эта точка называется вершиной угла, а полупрямые – сторонами угла. Если стороны угла перпендикулярны друг другу, то образуемый ими угол называется прямым (рис. 2,а). Углы меньше прямого называются острыми (рис. 2,б), а углы больше прямого – тупыми (рис. 2,в). Развернутым называется угол, обе стороны которого лежат на одной прямой (рис. 2,г); такой угол равен двум прямым углам. Биссектрисой угла называется прямая, проходящая через его вершину и делящая угол пополам. Углы можно измерять количественно, если определить единицу измерения угла (угол в один градус) как 1/180 развернутого угла. Таким образом, прямой угол содержит 90°, а угол на рис. 2,д содержит больше 180°, но меньше 360°.

На рис. 2,е, 2,ж, 2,з и 2,и показано, как соотносятся между собой углы некоторых фигур. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого (рис. 2,е). Вертикальные углы равны. Дополнительные углы в сумме составляют 90° (рис. 2,ж), а смежные углы в сумме дают 180° (рис. 2,з). Если прямая пересекает две параллельные прямые, как на рис. 2,и, то углы E, B, C и H равны, и углы F, A, D и G также равны между собой. Углы между параллельными (углы А, В, С, D на рисунке) называются внутренними, а углы, лежащие вне параллельных – внешними. Тот факт, что параллельные образуют с пересекающей их прямой равные углы, используется при вычерчивании параллельных прямых (рис. 2,м).

На рис. 2,к показано, как с помощью циркуля и линейки разделить пополам данный угол: прямая VA – биссектриса угла. На рис. 2,л показано, как удвоить данный угол.

Традиционно в элементарной геометрии выполнялись лишь геометрические построения, которые можно осуществить, используя только циркуль и линейку без делений. Общего подхода к таким построениям не существует, и успех почти целиком зависит от настойчивости и изобретательности. Так, например, может показаться, что задача о разделении угла на три равные части, т.н. трисекция угла, достаточно легка, поскольку сходная с ней задача деления угла пополам решается довольно просто. Однако на протяжении веков все усилия как любителей, так и профессионалов осуществить трисекцию угла неизменно оканчивались неудачей. Правда, эту задачу удалось решить, используя некоторые плоские кривые высших порядков, например, конхоиду и квадратриссу, а Архимед показал, как можно было бы решить задачу о трисекции угла с помощью линейки с двумя отметинами (рис. 2,н). В предложенном им решении задачи на ребре линейки откладывается расстояние МР, равное радиусу ON. Линейка кладется так, чтобы ее край проходил через точку N, тогда точка М попадает на продолжение прямой OL, а точка P – на окружность. Задача о трисекции угла эквивалентна поиску геометрического построения, позволяющего находить корни уравнения x 3 – 2 = 0. В 1837 вопрос о трисекции был окончательно решен французским математиком П.Ванцелем, давшим строгое доказательство невозможности точной трисекции угла в общем случае с помощью циркуля и линейки.

Треугольники.

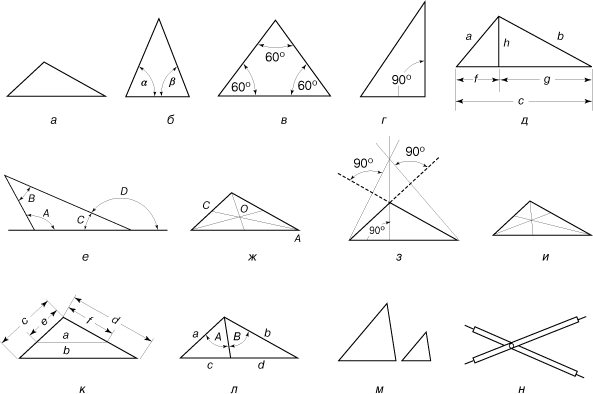
Треугольником называется плоская фигура, ограниченная тремя прямыми. У треугольника могут быть три неравные стороны (разносторонний треугольник), две равные стороны (равнобедренный треугольник) или три равные стороны (равносторонний треугольник) (рис. 3,а, 3,б, 3,в). В равнобедренном треугольнике углы, лежащие против равных сторон (углы a и b на рис. 3,б), равны; в равностороннем треугольнике все углы равны.

Длина перпендикуляра h, опущенного из вершины прямого угла на гипотенузу, есть среднее пропорциональное длин отрезков, на которые основание перпендикуляра делит гипотенузу:

Углы внутри треугольника называются внутренними; углы, которые образуются, если стороны треугольника продлить за их вершины, называются внешними (рис. 3,е). Сумма внутренних углов треугольника равна развернутому углу. Любой внешний угол равен сумме двух внутренних углов, не имеющих с ним общей вершины (РD = РA + РB).

Отрезок прямой, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой. Три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины. Например, на рис. 3,ж отрезок АО составляет 2/3 от длины отрезка АС. Точка пересечения медиан является также центром тяжести треугольника (треугольник, вырезанный из однородного по толщине и плотности материала и подвешенный в этой точке, будет находиться в равновесии). Высотой треугольника называется перпендикуляр, опущенный из одной из его вершин на противоположную сторону (или ее продолжение). Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром (рис. 3,з); биссектрисы всех углов треугольника также пересекаются в одной точке, которая является центром вписанной окружности (рис. 3,и) и равноудалена от всех сторон треугольника.

Прямая, пересекающая треугольник и параллельная одной из его сторон, делит две другие стороны на пропорциональные отрезки. На рис. 3,к a/b = e/c = f/d. Биссектриса любого угла треугольника делит противоположную сторону на отрезки, пропорциональные длинам сторон, образующих угол. На рис. 3,л, если РA = РB, то c/a = d/b.

Два треугольника (любые фигуры) называются равными (или конгруэнтными), если они переводятся друг в друга преобразованиями движения. Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояния между точками. Можно доказать три признака равенства треугольников: два треугольника равны, если 1) две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника; 2) сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ним углам другого треугольника; и 3) три стороны одного треугольника равны соответственно трем сторонам другого треугольника. Если треугольники можно перевести друг в друга преобразованием движения, не выводящим их из плоскости, в которой оба они лежат, то они называются собственно конгруэнтными; если же один из треугольников необходимо перевернуть, то треугольники называются несобственно конгруэнтными.

Преобразование одной фигуры в другую называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз. Две фигуры подобны, если они переводятся друг в друга преобразованием подобия.

Если два треугольника подобны (рис. 3,м), то их углы равны, а соответствующие стороны пропорциональны. Пропорциональным делителем, изображенным на рис. 3,н, пользуются для того, чтобы увеличить или уменьшить чертеж в требуемое число раз.

Площадь любого треугольника равна половине произведения его стороны на проведенную в ней высоту:

Если треугольник равносторонний, то его площадь равна 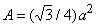, где а – длина стороны. Если а, b, c – длины сторон треугольника, то его площадь определяется по формуле

вывод которой приписывают Герону (s – полупериметр).

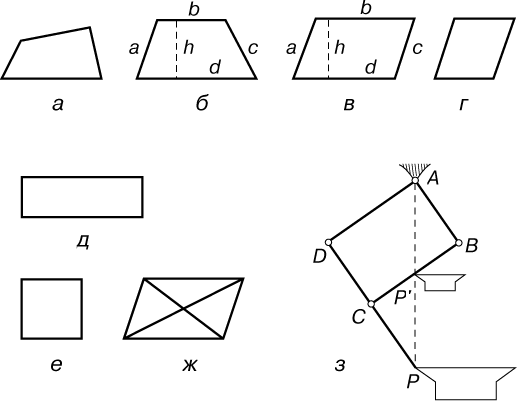
Четырехугольники.

Четырехугольником является всякая плоская фигура, ограниченная четырьмя прямыми (рис. 4). Параллелограммом называется четырехугольник, у которого противоположные стороны имеют равную длину. Ромб (рис. 4,г) – это параллелограмм, все стороны которого равны, а прямоугольник (рис. 4,д) – это параллелограмм, у которого все углы прямые. Диагонали параллелограмма (рис. 4,ж) в точке пересечения делятся пополам; в прямоугольнике диагонали равны. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие – непараллельны. Параллельные стороны называются основаниями. Площадь трапеции равна произведению высоты на полусумму ее оснований: A = h [(b + d)/2]. Площадь параллелограмма A = bh. Один из методов определения площади четырехугольника состоит в разбиении фигуры на два треугольника с помощью диагонали и в вычислении суммы площадей образовавшихся треугольников.

Интересным приложением свойств параллелограмма служит шарнирный пантограф (рис. 4,з), используемый для перечерчивания чертежей и других графических изображений в большем или меньшем масштабе. Пантограф представляет собой шарнирный механизм, имеющий форму параллелограмма, закрепленный в вершине А, со звеном DC, продленным до точки Р. Прямая РА пересекает звено СВ в точке Р ў. Звено СВ всегда параллельно звену DA, следовательно, треугольники PDA и PCP ў подобны. Поэтому CP ў = DAЧPC/PD, а эта величина постоянна, поэтому точка Р ў звена СВ также лежит на прямой, соединяющей точки Р и А. Из двух рассмотренных выше подобных треугольников следует, что отношение РА/Р ўА также постоянно. Следовательно, в любом положении пантографа перемещение точки Р ў пропорционально перемещению точки Р. Если точка Р движется по контуру какой-либо фигуры, то точка Р ў, в которой находится острие карандаша, повторяет без искажений этот контур в уменьшенном масштабе. Отношение масштабов оригинала и копии равно РА/Р ўА = PD/CD.

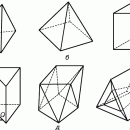
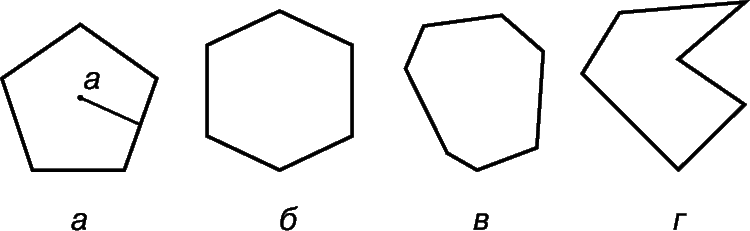
Многоугольники.

Многоугольником называется плоская фигура, ограниченная замкнутой ломаной линией, звенья которой называются сторонами. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. Выпуклый многоугольник называется правильным, если все стороны и углы его равны. Расстояние от центра правильного многоугольника до какой-либо его стороны равно радиусу вписанной в него окружности (обозначен на рис. 5,а буквой а). Площадь правильного многоугольника равна произведению половины радиуса на периметр:

В табл. 1 приведены названия и формулы для площадей некоторых правильных многоугольников (s означает длину стороны).

Таблица 1. НАЗВАНИЯ И ПЛОЩАДИ МНОГОУГОЛЬНИКОВ

Число сторон

Название многоугольника

Площадь правильного многоугольника

Источник